 | 教授。実際の製造現場では、誤差伝搬の法則を使ってないと言いましたよね?? | |
 | はい。 | |
 | そうすると、公差計算はどうやっているんですか?? | |
 | 製造現場でモノのばらつきを議論するときは、たいていの場合、それぞれの確率分布は正規分布に従うということを仮定しますね。そのうえで、公差計算を行います。前回も言いましたが、確率分布が分かってないと工程管理できないからです。 | |
 | 正規分布…。それ、いろいろなところで耳にしますね。 | |
 | そうですね。数ある確率分布の中でも、正規分布は別格ですからね。 | |
 | どうしてですか?? | |
 | それは中心極限定理が存在するからです。 | |
 | 中心…極限…。何か、物々しい定理ですね。 | |
 | 中心極限定理は、「任意の確率分布に従う母集団から抽出された標本の数が充分多い場合、標本平均の分布は正規分布に従う」というものです。 | |
 | 教授。何を言っているのか、さっぱり分かりません。 | |
 |
いま、6面のサイコロを振ることを考えてみましょう。それぞれの出目の確率はいくつですか?? 図1.サイコロを振ったときの出目の確率 |
|
 | 教授がインチキしてなければ、いずれも1/6の確率になります。 | |
 |
つまり、サイコロの出目の確率は一様分布しているわけです。ところが、このサイコロを2回振って、その平均値を計算するという試行を繰り返します。すると、こんなヒストグラムが得られます。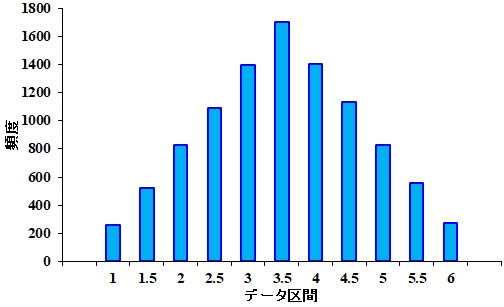 図2.サイコロを2回振ったときの出目の平均値のヒストグラム |
|
 | お。山型になってますね。 | |
 |
はい。今度は、10回振って、その平均値を計算するという試行を繰り返すと、こんなヒストグラムになります。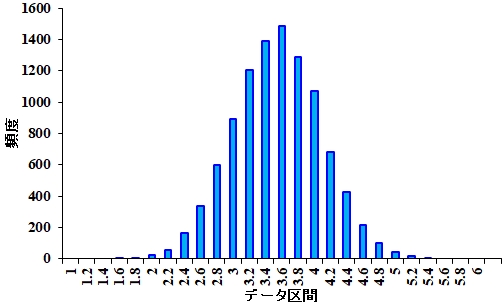 図3.サイコロを10回振ったときの出目の平均値のヒストグラム |
|
 | おお。何だか正規分布っぽく見えてきました。 | |
 | でしょう??オリジナルの確率分布は一様分布なのに、標本平均の分布をとると、その標本の数を大きくすればするほど、正規分布に近づくのです。しかも、この性質は一様分布に縛られるわけではありません。どんな分布でも、ちょっと操作すると正規分布が出現するのですから、正規分布が特別扱いされるのも無理からぬところでしょう。 | |
 | まさか、今からそれを証明しようと言うんじゃ…?? | |
 |
この証明はLindebergによって与えられました(論文)が、準備することが多くて、とてもここでは証明できません。
 Jarl Waldemar Lindeberg(1928~2017) |
|
 | あ~よかった。とりあえず、正規分布は別格だ、ということだけ覚えておきます。教授。この定理は、どんな確率分布でも成立するんですか?? | |
 |
はい、と言いたいところですが、中心極限定理が成立する条件というのが知られています。その条件から外れる確率分布は、この定理を満足しません。ただ、実用的な確率分布で中心極限定理を満たさないケースは稀ですから、あまり心配する必要はないでしょう。 |
~正規分布の重ね合わせ~
 | 教授。確率分布が正規分布だと、何かいいことありますか?? | |
 | 大ありです。正規分布は重ね合わせができるという非常に便利な性質を持っているんですよ。正規分布は、平均を\(\mu\)、標準偏差を\(\sigma\)とすると、 \[ \begin{align*} N\left( \mu \,,\ \sigma^2\right) \ =\ \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left[- \frac{\left(x-\mu\right)^2}{2\sigma^2} \right] \end{align*} \] と書けるんですが、確率変数\(X_1\)、\(X_2\)が互いに独立であり、それぞれ正規分布\(N\left(\mu_1\,,\ {\sigma_1}^2\right)\)、\(N\left(\mu_2\,,\ {\sigma_2}^2\right)\)に従っているとき、確率変数の和\(X_1+X_2\)は正規分布\(N\left(\mu_1+\mu_2\,,\ {\sigma_1}^2+{\sigma_2}^2\right)\)に従うのです。 | |
 | ん~と。つまり、正規分布の場合、単に標準偏差が伝搬するだけでなく、分布そのものも伝搬するということですか?? | |
 |
そういうことです。重ね合わせを計算するときは、畳み込み積分を使う必要があって、 \[ \begin{align*} g\left(z\right) = \int_{- \infty}^{\infty} \frac{1}{\sqrt{2\pi{\sigma_1}^2}} \exp\left[- \frac{\left(z-w-\mu_1\right)^2}{2{\sigma_1}^2} \right] \frac{1}{\sqrt{2\pi{\sigma_2}^2}} \exp \left[- \frac{\left(w-{\mu}_2\right)^2}{2{\sigma_2}^2} \right] dw \end{align*} \] を解かねばなりません。 |
|
 | 教授。寒気がしてきました。 | |
 |
この積分計算は、寒気がするほど難しくはないんですが、結果は、 \[ \begin{align*} g\left(z\right) = \frac{1}{\sqrt{2\pi}\sqrt{{\sigma_1}^2 + {\sigma_2}^2}} \exp\left[- \frac{\left(z-\mu_1-\mu_2\right)^2}{2\left({\sigma_1}^2+{\sigma_2}^2\right)} \right] \end{align*} \] となります。 |
|
 | 3分間クッキングみたいで、ナイスです。 | |
 | 元々の正規分布の式と比べてみてください。\(g\left(z\right)\)は\(N\left(\mu \,, \ \sigma^2\right)\)を、\(\mu\rightarrow\mu_1+\mu_2\)、\(\sigma^2\rightarrow{\sigma_1}^2+{\sigma_2}^2\)というように置き換えたものになってませんか?? | |
 | ウンウン。確かに、そうなってますね。 | |
 |
この性質は、確率変数がどれだけ多くなっても変わりませんから、正規分布をいくら重ねても正規分布になりますし、 \[ \begin{align*} \mu = \sum_{k=1}^{n} \mu_k \end{align*} \] \[ \begin{align*} \sigma^2 = \sum_{k=1}^{n} {\sigma_k}^2 \end{align*} \] が成立します。 |
|
 | 凄いですね、正規分布。 | |
 | あくまで、正規分布を仮定しないと成立しない議論ですが、たいていの偶然誤差は正規分布に従うことが分かってますし、何と言っても計算の取り扱いが便利ですから、対象としているばらつきに余程の矛盾がなければ、正規分布を採用します。 | |
 | 教授。光伝達効率も、このやり方で公差計算できますか?? | |
 | 当然です。まったく同じ結果になりますよ。 |
~計算上の注意点~
 | あれ??教授。ちょっと変じゃないですか?? | |
 | 何がです?? | |
 | 例えば、\(y=f\left(p_1 \,, \ p_2 \,, \ \cdots \,, \ p_n\right)\)として、関数\(f\)が複雑な形をしていた場合、\(p_1\)、\(p_2\)、…、\(p_n\)のそれぞれが正規分布だとしても、それに対応した\(y\)がいずれも正規分布になっている保証はないですよね?? | |
 | なかなかの指摘ですね。\(p_i\)をばらつかせて得られた\(y_i\)という集団が正規分布になっているかどうかは、確かに保証の限りではありません。 | |
 | もし、正規分布でなかった場合はどうするんですか?? | |
 | こういうスマートな議論が使えないわけですから、もし\(y\)の分布そのものを知りたいとすれば、例えばMonte-Carlo法などで計算して統計処理するしかないでしょうね。 | |
 | え~。Monte-Carlo法は、大量の乱数を発生させないといけないから、Excelが重くなるんですよ~。ファイルのやり取りが面倒になるので、やりたくないです。 | |
 | まぁ、たいていの場合、\(p_i\)をプラス/マイナス反転して変動させれば、\(y_i\)もそれに倣いますし、\(p_i\)に与える公差量も微小でしょうから、\(p_i\)が正規分布ならば、\(y_i\)も正規分布であると期待したところで、大きくは外れていないと思います。 | |
 | \(p_i\)をプラス/マイナス反転して変動させても、\(y_i\)が同じ方向にしか変動しなかったら―?? | |
 | そのときは、諦めてください。 | |
 |
がっかりです。そうすると、公差計算の手続きとしては、各パラメータが\(N\left(p_i \,, \ {\sigma_i}^2 \right) \)に従っているとして、 ①\(y\pm {\sigma^{\left(y\right)}}_i = f\left(p_1 \,, \ p_2 \,, \ \cdots \,, \ p_i\pm \sigma_i \,, \ \cdots \,, \ p_n\right)\)を計算する。 ②\( \{ {\sigma^{\left(y\right)}}_i \}^2\)を計算する。 ③\(1 \leq i \leq n\)にわたって、\(\{ {\sigma^{\left(y\right)}}_i \}^2\)を加算する。 でいいですか?? |
|
 | OKです。③の結果の平方根を以て、\(y\)の標準偏差が得られます。 | |
 |
教授。図面を見ると、たまに \[ \begin{align*} 30_{+0.1}^{+0.2} \end{align*} \] というような公差を見かけますが、その場合はどうするんですか?? |
|
 |
あ~。片側公差ですね。その場合は、中心振り分けに変換します。つまり、 \[ \begin{align*} 30.15_{-0.05}^{+0.05} \end{align*} \] という正規分布であると見なすわけです。 |
|
 | もし、全数検査をして、図面の公差から外れたものは搭載しないというような部品が混在する場合は、どう考えるんですか?? | |
 | つまり、その部品だけ選別する、ということですね。その場合も、Monte-Carlo法で処理するしかないと思います。 | |
 | でも、部品選別しなければ正規分布なんですよね??だったら、同じような積み上げ方が採用できませんか?? | |
 | できないです。部分的に正規分布であっても、部品選別してしまった時点で、そのパラメータの公差の意味が変わってしまうからです。 | |
 | 公差の意味?? | |
 | それについては、次回に説明しましょう。 |
| 前頁へ | 戻る | 次頁へ |