 | さて、前回の続きです。 | |
 | はい。 | |
 | 正規分布を使うもう1つのメリットとして、標準偏差を基準にして確率が議論しやすい、ということが挙げられます。 | |
 | 具体的に説明してください。 | |
 | 正規分布を\(\left[-\infty \,, \ \infty\right]\)の範囲で積分したら\(1\)になる、というのはいいですか?? \[ \begin{align*} P\left(- \infty \leqq X \leqq \infty\right)=\int_{- \infty}^{\infty} N\left(\mu \,,\ \sigma^2\right) dx =1 \end{align*} \] | |
 | 確率の総和を意味するから、当然ですね。 | |
 |
同じように考えれば、確率変数\(X\)が\(-\sigma \leq X \leq \sigma \)となる確率は、正規分布において\(\left[-\sigma \,, \ \sigma\right]\)の範囲で挟まれた面積と等しくなります。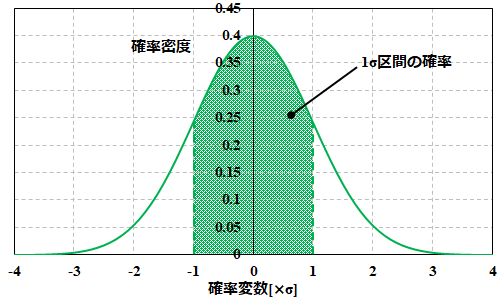 図1.\(-\sigma \leq X \leq \sigma\)となる確率 つまり、 \[ \begin{align*} P\left(- \sigma \leqq X \leqq \sigma\right)=\int_{- \sigma}^{\sigma} N\left(\mu \,,\ \sigma^2\right) dx =0.6827 \end{align*} \] です。例えば、ある長さのレールをたくさん製造したとして、その標準偏差を計算したら±0.2mmになったとしましょう。もし、公差を±0.2mmで与えていたとしたら、68.27%が合格品として出荷できる、ということになります。 |
|
 | なるほど。とすると、公差を±0.4mmで与えていたとしたら…。あれ??68.27%の2倍じゃないのか。 | |
 |
そのときは図2のように\(\left[-2\sigma \,, \ 2\sigma\right]\)で挟まれた面積を計算しないといけません。これは\(0.9545\)になります。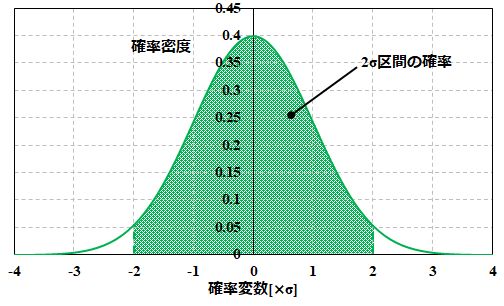 図2.\(-2\sigma \leq X \leq 2\sigma\)となる確率 |
|
 | え??どうやって計算するんですか?? | |
 | 残念ながら、この積分計算は解析的には解けません。ですので、数値計算するしかないんですが、正規分布はいろいろなところに顔を出しますので、標準正規分布表という便利なツールがあります。 | |
 | え〜。これ、見方が分からないし、目がチカチカします。 | |
 | Excelでも関数が用意されているので、計算できますよ。 | |
 | 関数を探して数式を組むのが面倒です。 | |
 | 世の中はありがたいことに、そういう横着者のために計算サイトも用意されています。 | |
 | それを早く教えてくださいよ〜。 | |
 | でも、このくらいの数字は、技術者の嗜みとして記憶しておくべきですね。\(\left[-3\sigma \,, \ 3\sigma\right]\)のときは\(0.9973\)、\(\left[-4\sigma \,, \ 4\sigma\right]\)のときは\(0.9999\)です。 | |
 | そうすると、公差を±0.4mmで与えていたとしたら、95.45%が合格品として出荷できる、ということなんですね?? | |
 | そのとおりです。そうやって考えると、標準偏差を基準にして、公差の意味が理解できます。 | |
 | 逆に、図面で設定した公差に対して、どのくらいの合格品を出すことができるのか、というふうにも考えられますね。 | |
 | その考え方を発展させれば、製造工程の能力を表す指標が作れそうだな、と思いませんか?? | |
 | 何だか、教授の誘導尋問に引っ掛かっている感じがして癪ですけど、確かにそう思えます。 | |
 |
実際、製造現場では、工程能力指数\(C_{\rm p}\)という指標が導入されています。
 Joseph Moses Juran(1904〜2008) |
|
 | それは、\(\pm \sigma\)を基準に考えるんですか?? | |
 |
いえ。それでは緩いので、\(\pm 3\sigma\)を基準に考えます。一般には、公差の下限値\({\rm LTL}\)と上限値\({\rm UTL}\)を使って、 \[ C_{\rm p} = \cfrac{({\rm UTL} - {\rm LTL})}{6 \sigma} \] のように定義されています。 |
|
 | そうすると、ある工程の標準偏差が\(\pm \sigma\)だったとき、図面公差が\(\pm 3\sigma\)と同じ値で与えられていたら、\(C_{\rm p}=1\)ということですね?? | |
 | はい。 | |
 | じゃぁ、図面公差を緩めた方が、出荷できる合格品の割合が多くなるから、Happyですね。 | |
 | と思いたくなるんですが、それは違います。 | |
 | え〜。何がいけないんですか?? | |
 | ユルユルの公差を設定してしまうと、工程の中で異常事態が起こっていたとしても、それを見逃してしまうリスクが発生するからです。これは工程管理の考え方においては、あってはならないことです。 | |
 | ということは、\(C_{\rm p}\)の適正な範囲というのがあるわけですね?? | |
 | はい。一般には、\(1.33 \leq C_{\rm p} \leq 2\)を適正な範囲とし、この状況であれば、抜き取り検査で合格/不合格をチェックして出荷してもよい、と判断します。 | |
 | \(C_{\rm p} < 1.33\)だったらどうするんですか?? | |
 | \(1.00 \leq C_{\rm p} < 1.33\)であれば、工程能力としては問題ないと判断しますが、\(1.33\)以上になるように工程を改善していくことが推奨されます。\(C_{\rm p} < 1.00\)のときは工程能力が低いとみなされ、全数検査ですね。 | |
 | 図面では、\(C_{\rm p}=1.33\)として公差を設定するんですか?? | |
 | いい質問ですね。一般的には、\(C_{\rm p}=1\)、つまり\(\pm 3\sigma\)で設定すると思います。 | |
 | そうすると、工程能力指数から公差を設定しているってわけでもなさそうですね。 | |
 | はい。ところが、実際に\(C_{\rm p}\)を運用している現場を見てみると、この辺の理解が不充分ではないか、と思われるケースが多々見受けられます。 | |
 | 例えば?? | |
 | 定義式では、\({\rm LTL}\)と\({\rm UTL}\)で計算するようになっているので、その数値を図面の公差そのままで運用する、といったケースです。 | |
 | でも、仮にそういう運用をしたとして、結果\(C_{\rm p} \geq 1.33\)だったら、より厳しく評価することになるわけだから、別にいいのでは?? | |
 | 結果論的には、それでいいのかもしれません。しかし、\(C_{\rm p} < 1.33\)となったとき、不要な工程改善などを行って、その分コストが膨らんでしまったとしたらどうでしょう?? | |
 | う〜ん。その分をプライスに反映すると、商品としての競争力がなくなるかもしれないし、プライスを据え置きにしたら利益が減っちゃいますね。 | |
 | そういうことです。やはり、ここは定義や背景、概念や本質的な考え方を正しく捉えて運用した方がよいと思います。 | |
 | 確かに。 | |
 | それと、図面の公差が\(\pm 3\sigma\)で記載されているかどうかは必ずしも自明ではない、という点にも注意が必要です。 | |
 | でも、それが一般的だって教授は言いましたよ?? | |
 | ですが、それは、あくまで一般の話だ、ということです。常に例外があり得ます。 | |
 | そうすると、±5mmと図面表記されていても、それは\(\pm 3\sigma\)かもしれないし、\(\pm 4 \sigma\)かもしれないってことですね?? | |
 | それならまだいいんですが、ひょっとしたら\(\pm 2\sigma\)かもしれない、\(\pm \sigma\)かもしれないわけです。 | |
 | え〜。そんな部品を掴まされたら、できあがった製品は不良ばっかりになるじゃないですか。 | |
 | ですから、特に新しい取引先とか、売り込みがあった場合には、「この図面に記載されている公差は\(\pm \sigma\)の何倍か??」ということを確認した方がいいのです。仮に、2つのメーカーに部品の設計をお願いし、同じ公差であるにも拘わらず、一方のメーカーの部品コストがやたら低い場合は、設定されている公差の裏にある考え方を疑った方がいいかもしれません。 | |
 | なるほどですね。 | |
 | そうでなくても、意外とメカ屋さんですら、自分が記載している公差が\(\sigma\)の何倍で設定しているのか曖昧な場合がありますからね。あまり分かった気になって試作や加工を進めない方がいいでしょう。手直しが発生すると、お金も時間ももったいないです。 | |
 | すべての公差は、\(\pm 4\sigma\)で記載するってことを標準化すれば、\(C_{\rm p}\)と整合的になって分かりやすいのにな。 | |
 | 誤解をなくすための抜本的解決としては、いい方法だと思います。 |
〜公差の意味〜
 | 教授。ちょっと気が付いたことがあるんですけど。 | |
 | 何でしょう?? | |
 | 例えば、\(C_{\rm p}=1.33\)だとしますよね。このときは、合格率は99.99%です。ということは、10,000個中1個は不良品が発生するわけですよね?? | |
 | 確率論的に考えれば、そういうことになりますね。 | |
 | 抜き取り検査だと、その不良品が合格品に紛れて出荷されてしまうことになりませんか?? | |
 | ここで議論している考え方に従えば、そういう状況は問題ないということになります。 | |
 | 何だか釈然としません。図面に書かれている公差は、OK/NGの判定基準だと思ってました。 | |
 | そういう考え方もあります。その場合の公差はワーストケースとみなされます。 | |
 | そっちの方が納得感が高いです。 | |
 | しかし、ワーストケースの考え方を採用した時点で、確率論は意味を失います。当然、誤差伝搬の法則も成立しません。 | |
 | ムムム。とすると、各パラメータの公差は、どうやって積み上がっていくんですか?? | |
 | ワーストケースと言うくらいですからね。どんどん加算的に積み上がっていきます。 | |
 | それじゃ、ダメなんですか?? | |
 | ダメじゃないですが、公差は厳しくなりますよ。例えば、10本のレールを足し合わせて、その結果の誤差を±1mmとしたい、ということを考えてみましょう。ワーストケースの考え方だと、各レールに与えるべき公差量は―。 | |
 | ±1mm÷10=±0.1mmですね。 | |
 | 一方、確率論的な考え方だと、±1mm÷√10=±0.31mmになります。 | |
 | おお。ずいぶん違いますね。 | |
 | これは、確率論で考えるメリットの1つですね。でも、これ以上に重要なのは、ワーストケースにおいては確率論が適用されないので、全数検査が必須であるという点です。 | |
 | つまり、コストが掛かるということですね。 | |
 | はい。それと、確率論的に考えると、たとえ1つの部品がマイナス側に不良だったとしても、プラス側に不良になった別の部品と組み合わせることにより、お互いの効果が相殺され、全体的な品質としては問題ない、となる可能性があります。 | |
 | う〜ん。 | |
 | 結局、製品で満足させるべきは最終品質です。もしワーストケースを採用すると、相殺できる可能性の芽を摘んでしまうことになるので、生産性に大きなダメージを与えてしまいますよね。 | |
 | う〜ん。でもな〜。1つの製品の中に、相殺する部品どうしが組み合わさらないかもしれないですよね?? | |
 | しかし、相殺する部品どうしが組み合わさるかもしれないじゃないですか。数を増やせば、相性のいい組み合わせの存在する可能性が高くなるように思えませんか?? | |
 | それは要するに、教授のことを気に入ってくれる女性は日本にはいないかもしれないけど、世界を見渡せばいるかもしれない、ということですか?? | |
 | …。つまり、確率論が成立するためには、ある程度のサンプル数が担保されてないとダメなんです。そういう意味で、ここでの考え方は大量生産にしか適用されません。 | |
 | そういうことか。 |
〜計算上の注意点、再び〜
 | 図面公差は、このように\(C_{\rm p}\)を含みに持たせた標準偏差を基準としたものか、ワーストケースかを区別して見ていかないといけないわけです。 | |
 | はい。 | |
 | そうすると、前に保留としてた問題の回答が見えてくるでしょう?? | |
 | 部品選別はワーストケースの考え方になるから、最終的な品質の分布を知りたければ、Monte-Carlo法にしないとダメだ、という話ですね。 | |
 | そういうことです。残念ながら、標準偏差とワーストケースは根本的な思想が異なるので、それを融合する理論的な計算方法はありません。ちなみに、ワーストケースを使った公差解析は互換性の方法、確率論を使った公差解析は不完全互換性の方法と言います。 | |
 | もし、何か法則性が見えてきて、独自の計算方法を確立できた場合は、それを使ってもいいでしょうか?? | |
 | 周りからの合意が得られれば、いいと思います。但し、考え方やリスクなどは、きちんと整理して、いつでも分かるようにしておく必要があります。もし社内に技術ガイドのようなマニュアルが制定されているのであれば、それは、まさにその思想の表れと言えるでしょう。 |
| 前頁へ | 戻る | 次頁へ |