 |
教授がこのあいだ発注した部品が納品されたので、分布をグラフにしてみたんですけど…。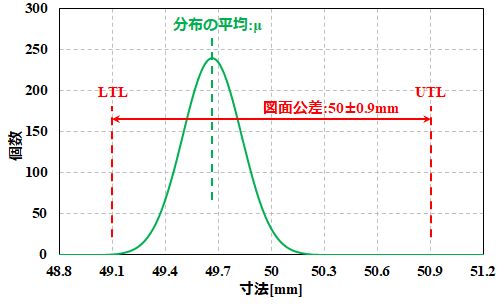 図1.偏りのある正規分布 |
|
 | なるほど。 | |
 |
この\(C_{\rm p}\)を計算すると、標準偏差が0.167mmで、公差が50±0.9mmなので、 \[ \begin{align*} C {\rm p} = \frac{(50.9-49.1)}{6 \times 0.167} =1.8 \end{align*} \] となります。 |
|
 | なるほど。 | |
 | でも、分布の平均は\(\mu\)=49.67mmなので、公差の中央値(50mm)からずれてます。 | |
 | なるほど。 | |
 | \(C_{\rm p}\)で議論していいのか、少し疑問が残るんですけど。 | |
 | なるほど。 | |
 | "なるほど"ばっかり言ってないで、私の疑問を解消してください。 | |
 | 分布に偏りがある場合の工程能力指数の考え方、というわけですね。 | |
 | そうです。 | |
 | 確かに、その場合は単純な\(C_{\rm p}\)は適用できません。その代わりに\(C_{\rm pk}\)という計算方法が用意されています。 | |
 | kが追加されましたね。 | |
 | \(C_{\rm p}\)はProcess Capability indexの略なんですが、kは"偏り"の頭文字です。 | |
 | え??え??日本語なんですか?? | |
 | そうですよ。 | |
 | 何か、ダサいです。 | |
 | こういう品質に対する考え方は日本が先駆的に開拓してきた歴史があって、そういうネーミングになっているわけですから、寧ろ誇りに感じていいと思いますけど。 | |
 | \(C_{\rm pk}\)はどう定義されるんですか?? | |
 | \(C_{\rm pk}\)は、 \[ \begin{align*} C_{\rm pk} = \frac{({\rm UTL} -\mu)}{3 \sigma} \end{align*} \] \[ \begin{align*} C_{\rm pk} = \frac{(\mu-{\rm LTL})}{3 \sigma} \end{align*} \] のうち小さい方を採用する、と定義されています。 | |
 |
定義もあんまりスマートじゃなくてダサいですね。そうすると、1番目の方は、 \[ \begin{align*} C_{\rm pk} = \frac{(50.9 -49.67)}{3 \times 0.167} = 2.47 \end{align*} \] で、2番目の方は、 \[ \begin{align*} C_{\rm pk} = \frac{(49.67 -49.1)}{3 \times 0.167} = 1.13 \end{align*} \] だから、\(C_{\rm pk}=1.13\)ということですね。 |
|
 | どうです??\(C_{\rm p}\)よりも小さくなってませんか?? | |
 | あ、本当だ。 | |
 | 偏りのある場合は、\(C_{\rm pk}\)に対して議論しないと、工程能力を正しく評価できないんです。気を付けましょう。 |
〜\(C_{\rm p}\)(\(C_{\rm pk}\))が違う場合〜
 | 教授。もう1つ疑問があるんですけど。 | |
 | 何でしょう?? | |
 | 部品Aと部品Bの\(C_{\rm p}\)を調べてみたら、一方は\(C_{\rm p}=1.33\)で、もう一方は\(C_{\rm p}=1.66\)でした。 | |
 | \(C_{\rm p}\)が違いますね。 | |
 | この場合、図面公差を使って積み上げの計算をしてもいいんですか?? | |
 | ダメですね。\(C_{\rm p}=1.33\)ということは、部品Aの公差は\(\pm 4\sigma\)のつもりで記載されてます。でも、部品Bは\(C_{\rm p}=1.66\)なので、公差は\(\pm 5\sigma\)のつもりで記載されているのです。単純に積み上げるわけにはいきません。 | |
 | やっぱり揃えないといけないですよね?? | |
 | そのとおりです。従って、\(\pm 4\sigma\)に揃えるなら、部品Bの公差の方を4/5倍して換算する必要があります。 | |
 | どうして、こんなことが起こっちゃったのかな〜?? | |
 | たぶん、設計者が加工区と綿密な打ち合わせをしなかったからじゃないですかね?? | |
 | ふ〜ん。 | |
 | ここで説明した考え方は、繰り返しになりますが、正規分布であるという仮定を置いていることを忘れてはいけません。仮定は、あくまで仮定でしかなく、本当はどうなっているか、設計者も理解しておく必要があると思います。 | |
 | 加工方法とか、加工する人によっても、何か違いそうですもんね。 | |
 | プレス加工などは、短期間で見れば正規分布で部品がばらつきますが、経年で金型が摩耗していくので、正規分布が徐々にシフトしていくような振る舞いをするはずです。また、ペレット樹脂を使って樹脂部品を射出成型する場合も、1ロットで見れば正規分布で部品がばらつくでしょうが、ロットの異なるペレット樹脂を使えば、平均も標準偏差も異なります。それと、片側公差の話を以前にしましたね。 | |
 | 覚えてますよ。中心振り分けにするんでしたよね?? | |
 | そうなんですが、加工区の方で部品の機能性を考慮し、例えば公差の大きい方へ偏らせて加工した方がいいと判断するかもしれません。 | |
 | そうすると、中心振り分けは間違ってますね。 | |
 | つまり、ここで説明した考え方は、計算のやりやすさを重視したものであって、必ずしも現実を反映していないリスクが内在していると認識した方がいいわけです。 | |
 | でも、すべての加工業者に、加工に対する思想みたいなことは訊けないですよ。 | |
 | はい。そこが悩ましい問題です。少なくとも、設計区は盲目的に計算手法だけを振りまわすのではなく、自分たちの扱っているやり方の限界は知っておいた方がいいと思います。 |
| 前頁へ | 戻る |