 | まず最初に宣言しておきますが、波動光学は難しいです。 | |
 | え〜、そうなんですか?? | |
 | はい。とても。 | |
 | とても?? | |
 | とても。 | |
 | 教授。今日はもう帰らせてもらいます。 | |
 | しかし、次に来ても簡単にはなりませんよ。 | |
 | う〜ん。難しい話は苦手なんだよな〜。 | |
 | そういう場合は、すべて理解しようとしない、というのが正しい学習態度と言えるでしょう。 | |
 | それでいいんですか?? | |
 | 自分がまず必要だと思うところを攻略して、そこから拡張していけばいいんですよ。それと、数式がいろいろ出てきますが、理論的概要の説明を苦手とする人は、そこを飛ばしても構いません。 | |
 | な〜んだ。だったら、面白そうな部分から頭に入れていきますよ。 | |
 | もう1つ、この講座は波動光学をメインにした技術について学ぶことが目的です。ですから、できるだけ理論的な話と技術的な話を結び付けて説明しますので、応用例を理解して、現象論としての波動光学を体得した後で、理論的な内容に戻ってくればいいんです。 | |
 | 了解です。ちょっとは、教授の話を聞こうという気になってきました。 | |
 | さて、波動の数学的表現は知ってますね?? | |
 | そのくらいは知ってますよ。三角関数です。 \[ u \left( \theta \right) = A \cos \theta \tag{1.1.1} \] | |
 |
三角関数は、横軸を角度\(\theta\)とすると、図1.1.1のようなグラフになります。
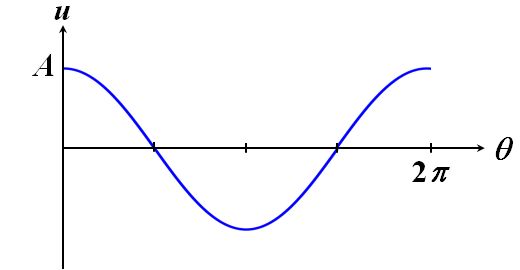 図1.1.1 三角関数 式1.1.1の\(A\)は振幅と言います。より正確には、最大振幅ですね。 |
|
 | 教授。振幅って、振れ幅ってことですよね??振れ幅って、最大値と最小値の幅を指しませんか?? | |
 | 確かに、振れ幅と言った場合はそうなりますが、振れ幅という物理用語はないんです。つまり、振れ幅≠振幅であり、振幅は振れ幅の\(\cfrac{1}{2}\)と定義できます。 | |
 | う〜ん、単に訳すのを失敗しただけのような気がしますけど、しょうがないので覚えます。 | |
 | 英語ではamplitudeと言うので、\(A\)で表現することが多いですね。さて、図1.1.1の繰り返し単位はいくつですか?? | |
 | \(2\pi\)です。 | |
 |
では、この繰り返し単位を拡張して\(\lambda\)と置きましょう。
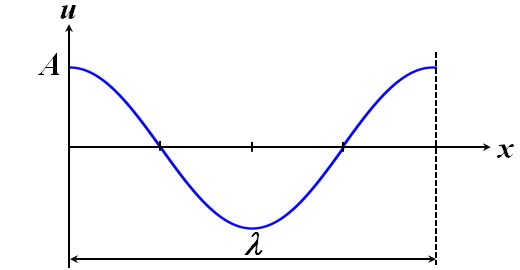 図1.1.2 三角関数の拡張 |
|
 | 横軸が\(x\)に変わりましたね。 | |
 | \(\lambda\)と\(2\pi\)、\(x\)と\(\theta\)はどんな関係にありますか?? | |
 | ムムム。単純な比例関係じゃないんですか?? \[ \theta : 2 \pi = x : \lambda \] | |
 | では、変形してください。 | |
 | こうですかね?? \[ \theta = \frac{ 2 \pi}{ \lambda } x \tag{1.1.2} \] | |
 | 式1.1.2を式1.1.1に代入すると?? | |
 | えいっ!! \[ u \left( x \right) = A \cos \frac{ 2 \pi}{ \lambda } x \tag{1.1.3} \] | |
 | 式1.1.3で導入された\(\lambda\)は、波動の性質を示すパラメータの1つで波長と言います。英語ではwavelengthですね。アルファベットの\(l\)はギリシャ文字だと\(\lambda\)なので、\(\lambda\)で表すことが多いです。 | |
 | 教授。式1.1.3は\(x=0\)で\(u(x)\)が最大値をとりますけど、波動を議論するときは、そうなるように座標系を設定しないといけないってことですか?? | |
 | まぁ、そういうやり方もありますが、その制約は使い勝手が悪い。ですから、汎用性を高めるために、初期位相\(\phi_0\)を式の中に仕掛けておきましょう。 \[ u \left( x \right) = A \cos \left[ \frac{ 2 \pi}{ \lambda } x + \phi _0 \right] \tag{1.1.4} \] 位相は英語でphase。アルファベットの\(p\)はギリシャ文字の\(\phi\)なので、\(\phi\)で表すことが多いですね。 | |
 | う〜ん。その位相っていうパラメータ、ちょっと抽象的ですね。他の振幅とか波長とは一線を画しているような…。 | |
 | なるほど。では、括弧の中を\(\cfrac{2 \pi}{\lambda}\)で括ったらどうでしょう?? \[ u \left( x \right) = A \cos \left[ \frac{ 2 \pi}{ \lambda } \left( x + \Delta l \right) \right] \tag{1.1.5} \] | |
 | つまり、 \[ \phi _0 = \frac{ 2 \pi}{ \lambda } \Delta l \] ってこと?? | |
 | はい。\(\Delta l\)は長さのディメンジョンを持つので、位相よりイメージしやすくなりますよね。これを光路長と言います。 | |
 | 光路の長さ??例えば、A地点からB地点の光路の長さって、単純なAB間の距離とは違うんですか?? | |
 | 厳密には違います。光路長は光学的距離とも言いますが、要するに「光が感じる距離」なので、屈折率の作用を考慮しないといけません。ですが、ここでは真空中の光の伝搬という条件を置いて、屈折率は\(1\)としておきましょう。ちなみに、単純なAB間の距離は、光学的距離と区別するために幾何学的距離と言うこともありますね。 | |
 | 真空中だと、光路長=幾何学的距離?? | |
 |
そういうことです。 |
|
 | 光路長の方がイメージしやすいのに、わざわざ位相に直すのかぁ。 | |
 | その方が議論しやすいからですよ。ポイントは、波動というのは、波長を1つの単位としたパターンの連続で表現される、という点です。だから、対象としている波動が近いか遠いかというのは、波動の本質を理解する場合、どうでもいいのです。波長の単位で同じ現象がコピーされているので、寧ろ位相に変換した方がずっとスマートです。 | |
 | つまり、波動を議論する場合は、光路長を位相に変換するひと手間が必要だってことですね?? | |
 | そうです。光路長に\(\cfrac{2\pi}{\lambda}\)を掛けて位相に変換する。これは、後で干渉とか回折などを勉強するときに頻繁に出てくるので、覚えておくとよいでしょう。 | |
 |
教授。波動って、水面に雫を垂らしたときに発生する波紋が具体的な事例だと思うんですけど、式1.1.4では、それを上手く表現できてない気がします。
|
|
 | そのとおりです。動画から分かるように、波紋は動いているように見えますよね。動いているというのは、物理学的に「時間の関数として表現できる」と翻訳することができます。でも、式1.1.4には時間のパラメータがありません。 | |
 | 確かに。だから、波動が動いていることを表現できてないんですね。 | |
 |
そこで、次のようなことを考えます。図1.1.3を見てください。この図では、ある時刻における波動をブルーで、この波動が速度\(v_p\)で移動して、ある時間\(t\)が経過した後の波動をピンクで示してます。
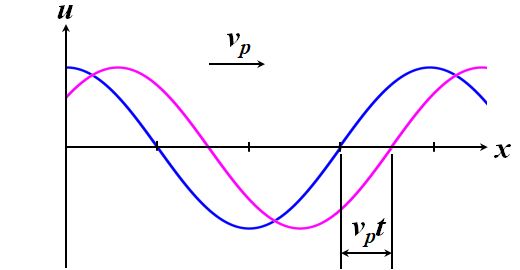 図1.1.3 時間の概念を導入した波動関数 |
|
 | ブルーとピンクの移動距離は\(v_p t\)ってことですね。 | |
 | この速度\(v_p\)は位相速度と言います。 | |
 | 単に速度って言わないのは、何か理由があるんですか?? | |
 | 波動を特徴づける物理量としては、他に群速度などがありますからね。誤解のないように区別します。尤も、先ほど真空中の光の伝搬という条件を置いたので、位相速度と群速度は一致します。 | |
 | 気にしなくてよい、と。 | |
 | そういうことです。さて、ピンクの波動を式で表してください。 | |
 | う〜ん。\(v_p t\)だけ後ろにずれると式1.1.4になるんだから、 \[ u \left( x,t \right) = A \cos \left[ \frac{ 2 \pi}{ \lambda } \left( x - v_p t \right) + \phi _0 \right] \tag{1.1.6} \] こうかな。 | |
 |
ここで、波動を構成している1つの質点の運動に注目しましょう。この質点は、波動の位相速度の方向に運動しているわけではありません。その場で上下運動しているだけです。
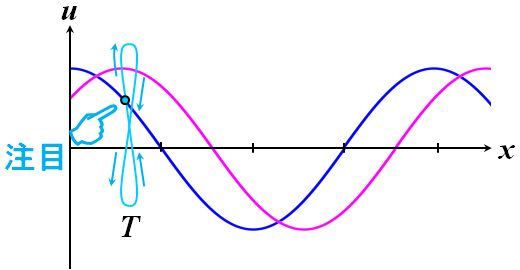 図1.1.4 質点に注目(便宜的に8の字で描いている) |
|
 | ん??そうですか?? | |
 |
では、次の動画を見てください。
|
|
 | お〜。綺麗なウェーブですねぇ。私もやったことありますよ。 | |
 | だったら話は早い。この動画は、2011年の日本シリーズで起きた観客席のウェーブの様子ですが、ウェーブを構成している1人1人は、どんな運動をしてますか?? | |
 | ん??う〜ん、その場で立ったり座ったりしているだけですね。 | |
 | その運動が、隣の人と微妙にずれていることで―。 | |
 | ウェーブが発生しているように見えるのかぁ。 | |
 | つまり、波動を構成している1つ1つの質点の運動は、その場での上下運動だと考えられます。 | |
 | そう言われると、反論の余地ないですね。悔しいけど。 | |
 | 例えば、池の真ん中に1万円札がプカプカ浮いている様子をイメージしてください。どうしたいですか?? | |
 | そりゃ、getしますよ〜。 | |
 | どうやりましょう?? | |
 | 長い棒を探します。 | |
 | なかったら?? | |
 | う〜ん。その辺の小石を拾って、波紋を発生させるかな。 | |
 |
しかし、今の議論を振り返ると、波紋を発生させても無駄だということが分かりますよね??
|
|
 | あっ!!波紋を発生させている水分子は上下運動しているだけだから、1万円札もその場で上下運動するだけ?? | |
 | 理屈上は、こっちに移動することはありません。尤も、実際は1万円札の重力とか摩擦とか、いろいろな力が働いているので、根気よく小石を投げ続ければ、いずれgetできますけどね。 | |
 | 私、そういう点では我慢強いから大丈夫です。 | |
 | いや、そういう根性論はどうでもよくって、波動の本質というのは、質点が移動しているのではなく、エネルギーだけが伝搬している、っていうことです。 | |
 | 普通、波動を議論するときは、観客席のウェーブのように単発の波動は取り上げませんよね?? | |
 | そうですね。何度も何度もウェーブが発生する波動が対象になります。従って、質点も上下運動を繰り返すことになりますね。そこで、質点に注目したときの繰り返し時間を\(T\)としましょう。これを周期と言います。 | |
 | 周期って英語でperiodですけど、\(T\)で表すんですね?? | |
 | そうですね。どっちかと言うと、timeの方を採用しているようです。さて、質点が1周期だけ運動すると、波動は1波長分だけ進んでますね?? | |
 | はい。 | |
 | これを数式で表現してください。 | |
 | う〜ん。こうかな。 \[ v _p T = \lambda \tag{1.1.7} \] | |
 | では、式1.1.7を式1.1.6に代入すると?? | |
 | こうですね。 \[ u \left( x,t \right) = A \cos \left[ \frac{ 2 \pi}{ \lambda } x - \frac{ 2 \pi}{ T } t + \phi _0 \right] \tag{1.1.8} \] 何か、ゴチャゴチャしてきましたね。 | |
 | では、 \[ k = \frac{ 2 \pi }{ \lambda } \tag{1.1.9} \] \[ \omega = \frac{ 2 \pi }{ T } \tag{1.1.10} \] と置きましょう。 | |
 | つまり、 \[ u \left( x,t \right) = A \cos \left[ k x - \omega t + \phi _0 \right] \tag{1.1.11} \] ですね。 | |
 | これが、波動を表現する一般式の1つになります。ちなみに、\(k\)は波数、\(\omega\)は角速度と言います。 | |
 | 波数はwave numberですよね??\(k\)?? | |
 | 個数を表現するのに、よく使われる記号だからですよ。 | |
 | 角速度はanguler velocityですよね??\(\omega\)??時計屋の陰謀?? | |
 | これはよく分からないですね。でも、物理学の世界では、かなり定着している印象があります。 | |
 | 教授。式1.1.11は1次元ですよね?? | |
 | そうです。もちろん、ベクトルを使って3次元空間への拡張もできますよ。 | |
 | ベクトル?? | |
 | つまり、\(x\)の代わりに位置ベクトル\(\vec{\mathstrut v}=(x,y,z)\)に変えればいいんです。 | |
 | 波数の方も合わせないとダメでは?? | |
 | 波数ベクトル\(\vec{\mathstrut k}=(k_x,k_y,k_z)\)に変えます。よって、 \[ u \big( \vec{\mathstrut r},t \big) = A \cos \big[ \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \big] \tag{1.1.12} \] | |
 | 位置ベクトルと波数ベクトルの内積を計算するんですね?? | |
 | そうです。もう少し言っておくと、三角関数は計算の取り扱いが面倒なので、普通はEulerの公式を使って、指数関数表示するのが一般的ですね。 | |
 | Eulerの公式って、虚数が入ってますけど?? \[ u \big( \vec{\mathstrut r},t \big) = A \exp \Big[ i \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \big) \Big] \tag{1.1.13} \] | |
 |
ですので、波動を具体的に取り扱うときは、三角関数に変換し、実部だけを議論の対象にします。Eulerの公式は数学的な計算をするうえでの便宜的な表現と割り切ってください。これで、平面波の一般式が導けたことになります。平面波は、こんな波動ですね。
|
|
 |
てことは、かめはめ波は平面波ですね。
|
|
 | う〜ん。考えたことないですけど、今度、柳田理科雄に訊いておきますよ…。 |
| 戻る | 次頁へ |