 | 教授。Galileo、Rømerと見てきましたけど、一向に光速のまともなデータが出てきませんよ。 | |
 |
そうですね。では、そろそろ真打に登場してもらいましょう。Rømerの後、光速の測定にチャレンジしたのは、イギリスの天文学者であるBradleyです。
 James Bradley(1693~1762) |
|
 | やっぱり天文学なのか。 | |
 |
当時の天文学は、Keplerによって提唱された地動説が主流になりつつありましたが、Bradleyはその証拠となる年周視差の測定に力を入れていました。
 Johannes Kepler(1571~1630) |
|
 | 年周視差?? | |
 |
地球が太陽の周りを公転しているとすれば、恒星・地球・太陽とで大きな三角形が作られます。この頂点の角度が年周視差です。
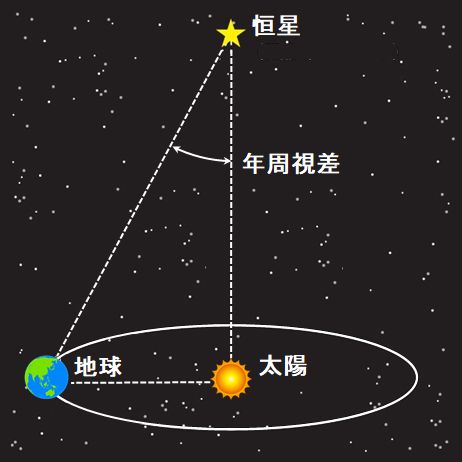 図1.5.23 年周視差 地動説が正しければ年周視差が存在する、ということはずいぶん前から知られていたことで、Bradleyもそれに着目したわけです。しかし、この試み自体は失敗します。 |
|
 | なぜですか?? | |
 |
地球から最も近い恒星は、ケンタウルス座のα星ですが、
 図1.5.24 ケンタウルス座α星 それでも年周視差は僅か0.76秒しかありません。残念ながら、当時の測定精度で検知するには小さすぎたのです。 |
|
 | そっか…。 | |
 |
この測定が可能になるのは、更に100年くらい後の1838年のことです。Besselという天文学者が、はくちょう座61番星の年周視差=0.314秒であることを突き止めたのが最初です。
 Friedrich Wilhelm Bessel(1784~1846) そういうわけで、Keplerが地動説を唱えたときも、その師匠に当たるTycho Braheは、年周視差が観測できないことを以て、その説を否定しています。  Tycho Brahe(1546~1601) |
|
 | 年周視差って、重要な証拠だったんですね。 | |
 | ところが、Bradleyは、その証拠探しの過程で、偶然にも光行差という現象を発見するのです。 | |
 | 光行差?? | |
 |
Bradleyが観測の対象としていたのは、りゅう座のγ星です。
 図1.5.25 りゅう座γ星 この恒星の年周視差を観測したデータを調べていたところ、Bradleyは年周視差では説明のつかない奇妙なずれがあることに気が付きます。年周視差を観測するためには天体望遠鏡はいずれの季節でも、太陽に向かうベクトルと、それに垂直なベクトルの合成になってないといけません。しかし、太陽に向かうベクトルに対して僅かにずらして天体望遠鏡をセットしないと、恒星が観測できなかったのです。 |
|
 | 何だか、こっちの話もミステリアスでいいですねぇ。 | |
 |
この問題はBradleyを大いに悩ませますが、1728年の秋にテムズ河のヨット遊びに参加した際、その解決のヒントを手に入れます。例えば、雨が降っているとしましょう。立ち止まっていれば、傘は図1.5.26のように差します。
 図1.5.26 雨が降ったら傘を差す では、自転車に乗っている場合はどうしましょう?? |
|
 | 教授。それは道交法第71条第6号で禁止されてますけど?? | |
 | 今は特例措置ってことで。 | |
 |
図1.5.27ですかね??
 図1.5.27 自転車に乗っているときの傘の差し方 |
|
 | なぜですか?? | |
 | なぜ?? | |
 | なぜ、傘を斜めに差すんですか?? | |
 | だって、顔が濡れちゃうじゃないですか。 | |
 | でも、雨は上から降っているんですよ?? | |
 | う~ん。雨は上からかもしれないけど、自転車は前に進んでいるから、乗っている人からすれば、雨が斜め前から降っているように感じますもん。 | |
 |
はい。つまり、Bradleyが気が付いたのも、それなんです(図1.5.28)。地球の真上に恒星がある場合、地球が公転してなければ、天体望遠鏡は天頂方向にセットすればいい(a)。しかし、恒星から降り注ぐ光を、公転している地球から観測するとすれば、傘を斜めに差したように、天体望遠鏡も斜めにセットしないとダメだ、ということなんですよ(b)。
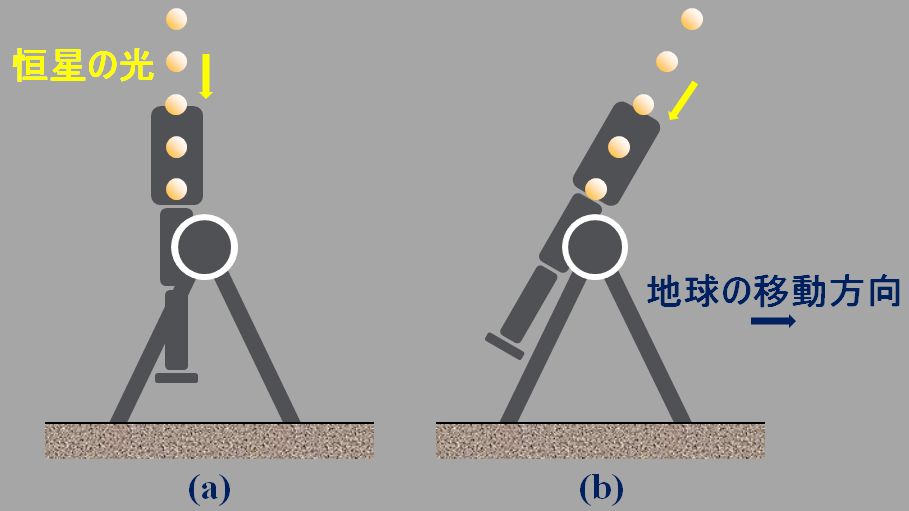 図1.5.28 光行差 これが、光行差という現象です。 |
|
 | な~るほど。ん??てことは、これも地球が動いている証拠になるのでは?? | |
 | そのとおりです。年周視差を観測することはできませんでしたが、奇しくも光行差によってBradleyは地動説を証明することになったのです。 | |
 | 転んでも、タダでは起きませんねぇ。 | |
 |
図1.5.28(b)を見ると、図1.5.29のような関係が成立することが分かりますね(\(v\)は地球の公転速度)。
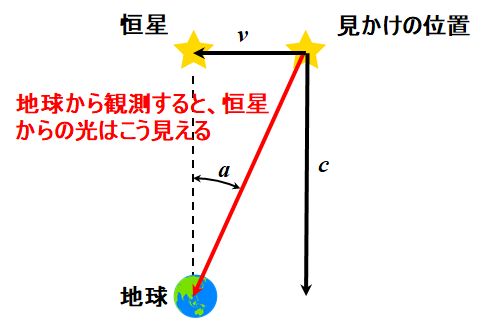 図1.5.29 光行差で生じるずれ\(a\) 式で書くと―。 |
|
 | こうかな。 \[ v = c \times \tan a \approx ca \tag{1.5.1} \] | |
 | 地球の公転半径を\(R\)とすると、太陽からの光が地球に届くまでの時間\(t\)は、 \[ t = \frac{ R }{ c } \tag{1.5.2} \] です。一方、地球が太陽の周りを1回転する時間を\(T\)(=1年)とすると、 \[ T = \frac{ 2 \pi R }{ v } \tag{1.5.3} \] なので、式1.5.2に式1.5.1と式1.5.3を代入して整理すると―。 | |
 | こうなりました。 \[ t = \frac{ v T }{ 2 \pi c } = \frac{ ca T }{ 2 \pi c } = \frac{ a T }{ 2 \pi } \] | |
 |
\(a\)はBradleyの論文(論文)によると20.2秒ですから、具体的な数字を入れて計算してみてください。
 図1.5.30 論文抜粋 |
|
 |
えっと、20.2秒はラジアンに直さないといけない(=9.793×10-5rad)から、 \(t\) = ( 9.793×10-5 rad × 365 日 ) ÷ ( 2 × 3.14 ) ≒ 8 分 12 秒 かな。 |
|
 | というわけで、論文の数字が導けました。 | |
 | お~、凄い。 | |
 | つまり、Bradleyは、①光速は有限であり、②太陽からの光は8分12秒かかって地球に届く、と主張したわけです。 | |
 | ん??でも、光速そのものは求めてないのでは?? | |
 |
そうですね。式1.5.2を使えば求められますが、恐らくBradleyは当時知られていた地球の公転半径のデータを信用してなかったのだと想像されます。だから、光速ではなく飛行時間で代用したんでしょう。前回、\(R\)=1億5,000万kmだと言ったので、それを使って計算すると、 \(c\) = 1億5,000万 km ÷ 8 分 12 秒 ≒ 3.05×108 m/s となり、Bradleyの値もかなりいい線いってたな、ということが分かります。 |
|
 | そうかぁ。結局、測定精度が問題になるわけですね。 | |
 | ただ、Bradleyは光速の有限性を明確に主張し、太陽から地球までの光の飛行時間を確定した点で、Rømerとは一線を画していると思います。 |
| 前頁へ | 戻る | 次頁へ |