 | 前回のFizeauの実験はかなり大掛かりでしたけど、もう少しお手頃な測定方法はないんですか?? | |
 |
ラボ・レベルでの光速の測定となると、Foucaultでしょうかね。では、最後にFoucaultの方法について触れておきましょう。
 Jean Bernard Lèon Foucault(1819~1868) |
|
 | ラス・ボス登場って感じかな。 | |
 | Foucaultは学校の勉強はからっきしダメだったんですが、手先が器用だというので、医者の道を志します。 | |
 | 学校の成績が悪いなんて、何だか親しみが湧きますねぇ。 | |
 | ところが、この人は血を見るとひっくり返るという悪い癖があり、医者の道を断念します。 | |
 | 親近感、倍増~。 | |
 | そのうち、Fizeauと出会って物理学の道に転向するのです。 | |
 | ん??Fizeauって、前回の?? | |
 | はい。しかし、Fizeauの方は正規の教育で物理学を履修した一方で、Foucaultは元々医者を目指していた関係上、物理学では在野の研究者という位置づけになります。実は、このことが後になってFoucaultを悩ませる事態に発展するんですが、それは追々話しましょう。Foucaultは手先が器用であることと、抜群の実験センスで、数々の偉業を成し遂げます。その1つがFoucaultの振り子実験ですね。 | |
 | 振り子?? | |
 | 我々は地球が自転していることを知ってますが、もし、そのことを証明しろって言われたらどうしましょう?? | |
 | 人工衛星を打ち上げて、外から観測すればいいじゃないですか。 | |
 | それは1つの方法ではありますが、世界初の人工衛星はスプートニク1号で、1957年の話ですよ。Foucaultの時代では無理な相談です。 | |
 | う~ん。地球にいながらにして証明ってことかぁ。 | |
 | 何と、Foucaultはその方法を考案する(論文)のです。 | |
 | できるってことですか??どうやって?? | |
 |
パリ天文台のメリディアン・ホールの天井から巨大な振り子をぶら下げて、それを振ったんですよ。
 図1.5.37 パリ天文台 |
|
 | 振り子を振って証明??たったそれだけ?? | |
 |
例えば、中華料理を食べに行ったときに見掛けるターン・テーブルを思い起こしてください。そのターン・テーブルが一定の速度で回転しているとしましょう。そのテーブルの周辺から中心に向かってボールを転がすと、テーブルの外側の静止系では、ボールは真っすぐ運動しているように見えます。
|
|
 | そうですね。 | |
 |
しかし、テーブルの座標系から、このボールの運動を観察すると曲がって見えます。
|
|
 | ほぉ。確かに。 | |
 |
回転するテーブルにいる人からすると、あたかもこのボールに何らかの力が働いているように見える。この見掛けの力をCoriolis力と言います(論文)。
 Gaspard-Gustave Coriolis(1792~1843) |
|
 |
あれですよね、北半球の台風がいつも左まわりってやつ。
 図1.5.38 北半球の台風はCoriolis力によっていつも左まわりとなる |
|
 | そうです。とすれば、天井から吊り下げた巨大な振り子にも、このCoriolis力が働かないとおかしいですね?? | |
 | ふむ。 | |
 |
だから、この振り子を放っておくと、ブンブン揺れながらジワジワ回転していくはずだ、ということにFoucaultは気が付くのです。
|
|
 | お~、ナイス・アイデア。これ、どこに行ったら見られるんですか?? | |
 | この手の実演装置は、巨額のコストが発生するわけでもないですし、展示品としては目玉になるので、いろいろな博物館で見ることができますよ。例えば、国内だと国立科学博物館が有名ですね。 | |
 | そこに行けば、クルクルまわっているのが観察できるのかぁ。 | |
 | しかし、1周するのに41時間かかりますからね。かなり辛抱強く観察しないと、移動している様子は把握できないですよ。 | |
 | ん??41時間??それはおかしいですよ。1日は24時間じゃないですか。 | |
 | いえ。振り子の振動面の周期は、振り子を設置した緯度に応じて変わります。これをFoucaultの正弦則と言います。 | |
 | え??そうなの?? | |
 |
よく考えてみてください。仮に、振り子を北極、或いは南極に設置したとすると、地球の外から見たときの振動面は変わらず、地球の方が24時間で1周するので、逆に地球から振り子の振動面を観察すると、振動面は24時間で1周することになります。
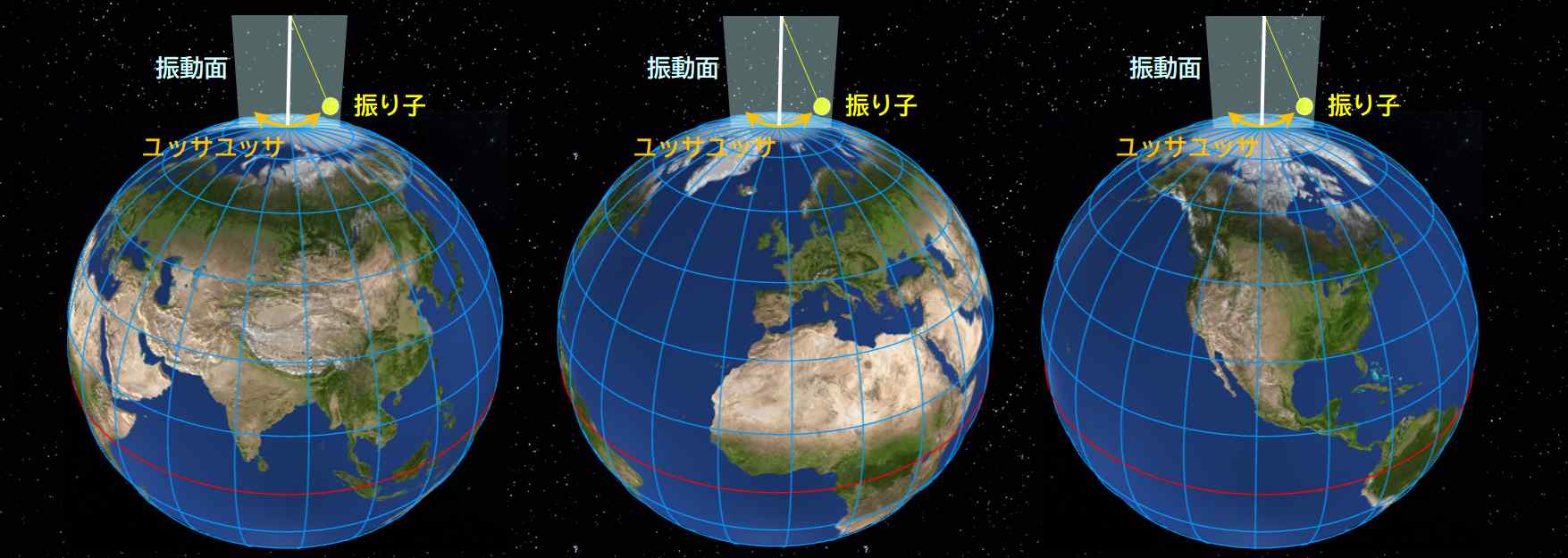 図1.5.39 極にいる人は振動面が24時間で1周するのを観察する |
|
 | でしょ?? | |
 |
が、振り子を赤道上に設置した場合、ある時点での振動面を南北方向に設定したら、どの時点でも振動面は南北方向のままです。
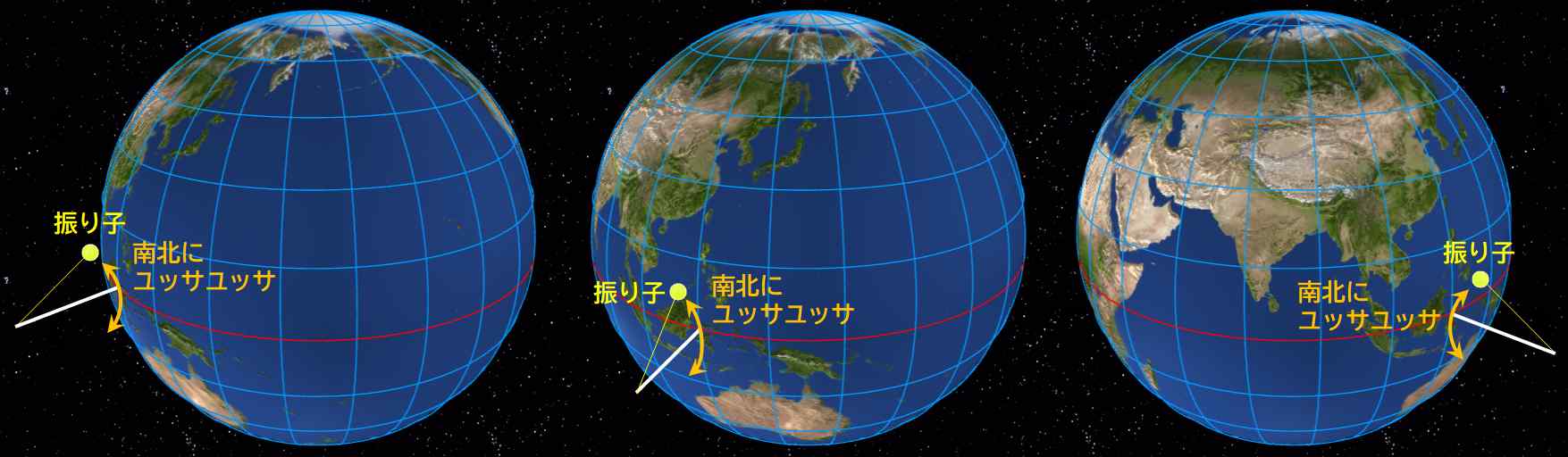 図1.5.40 スラウェシ島では振動面の回転は観測できない |
|
 | ん~。つまり、赤道上ではCoriolis力は働かないってこと?? | |
 | そうですよ。そもそも、Coriolis力というのは、「緯度ごとに自転速度が異なる」ことが発生要因ですから。 | |
 |
緯度ごとに自転速度が異なる…。あ、そうか。どの緯度でも1日24時間は変わらないけど、赤道から離れるにつれて、1周する距離は短くなりますもんね。
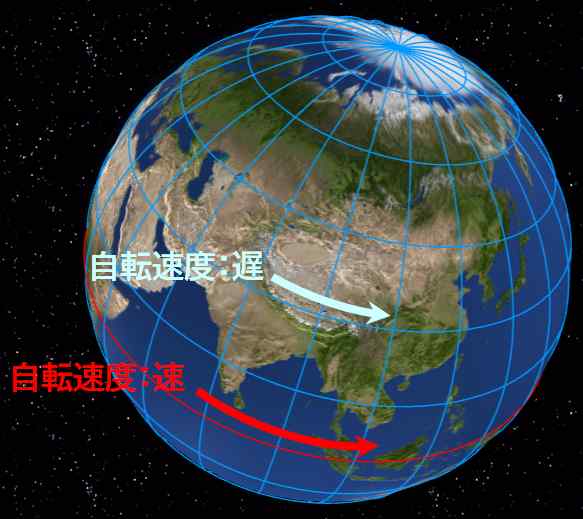 図1.5.41 緯度と自転速度の関係 |
|
 |
もし、地球の形が円筒形だとすると、緯度によって自転速度が変わることはありません。よって、赤道のある1点Pから南北方向に旅立った飛行機は、どの高さ(緯度)であろうと、点Pを通る南北方向の線上に着陸します。
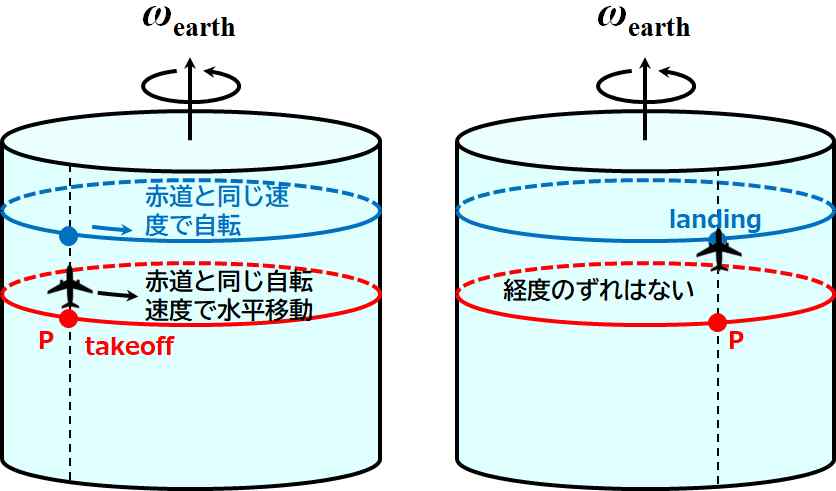 図1.5.42 地球が円筒形だったら… |
|
 | はい。 | |
 |
しかし、地球は球形をしているため、飛行機は同じように南北方向に旅立っているにも関わらず、地球の表面は赤道から離れるにつれて遅く移動(自転)しているので、着陸する地点が点Pを通る南北方向の線上からずれてしまうのです。
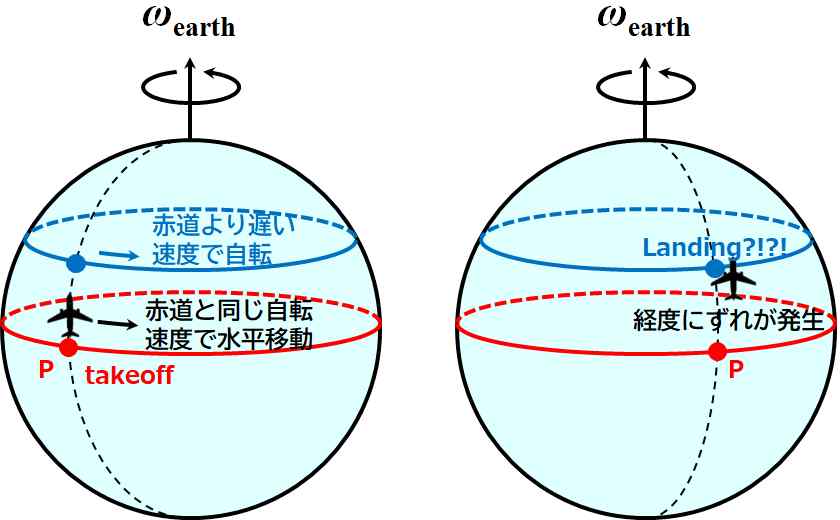 図1.5.43 地球は球形なので… |
|
 | ということは、赤道から南北方向に同じだけ移動した場合は、北緯と南緯で自転速度が同じだから、影響が相殺されてCoriolis力は働かないのか。 | |
 | だから、振り子の振動面は回転しないのです。 | |
 | てことは、振動面の周期は\(0\)?? | |
 | 違います。回転するのに無限の時間がかかっていると考えるので、周期は\(\infty\)です。 | |
 | ということは、極から赤道に向かって、振り子の振動面の周期は24時間から\(\infty\)まで変化するわけですね。 | |
 |
振動面の回転は、地球の角速度ベクトル\(\omega_{\rm earth}\)の、振り子を設置した緯度における法線成分が生み出しているので、緯度を\(\psi\)とすると、振動面の角速度ベクトル\(\omega_{\rm swing}\)は、
\[
\omega_{\rm swing} = \omega_{\rm earth} \sin \psi
\]
です。
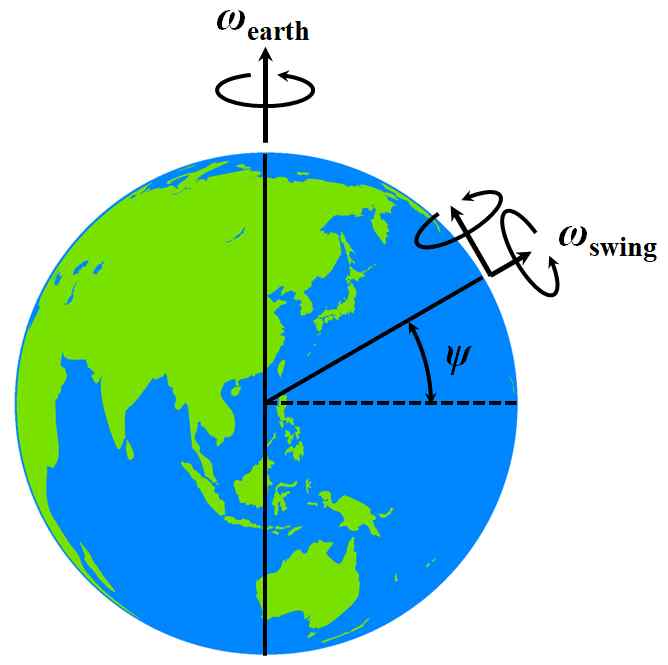 図1.5.44 振動面の角速度ベクトル |
|
 | だから、振動面の周期\(T_{\rm swing}\)は、 \[ T_{\rm swing} = \frac{ 2 \pi }{ \omega_{\rm swing} } = \frac{ 2 \pi }{ \omega_{\rm earth} \sin \psi } = \frac{ 24 }{ \sin \psi } \] になるのか。 | |
 | 国立科学博物館は北緯35度43分なので、これを代入すれば41時間という結果が得られます。Foucaultは、この正弦則を直感で導いたと言われてますね。 | |
 | 直感??凄いですね!! | |
 |
正弦則の最初の数学的な証明は、Liouvilleによって与えられました。
 Joseph Liouville(1809~1882) ただ、この一連の議論は近似的には問題ないのですが、厳密性を追い求めると、どうしても実験結果との差が不可避的に出てきてしまいます。どうやら、Kirchhoffはそれに不満だったようで、その解決を教え子のOnnesに博士論文のテーマとして与えるのです。  Heike Kamerlingh Onnes(1853~1926) |
|
 | 博士論文になるだけのテーマってこと?? | |
 | ですね。何しろ、仕上がった論文(論文)は、280ページくらいありますから。 | |
 | 読む気が起きませんね…。 | |
 | Foucaultの振り子実験は、深追いすると非常に複雑で難解なテーマであることは間違いありません。実際、振り子の運動は、単純な振動をしているわけではなく、その軌跡はLissajous曲線となります。 | |
 | でも、そこを直感で斬り込んで、振り子のみで自転を証明したFoucaultの着眼点は、驚きですね。 | |
 | そうですね。実にシンプルで鮮やかな証明方法です。しかし、これが実はあらぬ疑いを招くことになりました。 | |
 | 疑い?? | |
 | これを見た当時の数学者・物理学者たちは、こんな簡単な方法で自転の証明ができるなんて、昔の偉大な物理学者、例えばNewtonとか、da Vinciだとか、Keplerだとかが気が付いてないはずがない、と思ってしまうわけです。つまり、Foucaultは昔の物理学者の方法をパクッたんだ、と指摘したのです。 | |
 | え~、剽窃疑惑??科学では、あってはならないことじゃないですか。 | |
 | 恐らく、その背景にはFoucaultが在野の研究者だという事実もあったのでしょう。学会は過去の文献を徹底的にひっくり返し、パクリの証拠を探し始めます。しかし、どうしても見つからない。どうやら、この方法はFoucaultのオリジナルだということで決着するものの、それまで地球の自転を証明することは不可能だと断定していた専門家たちは、Foucaultのせいで面目丸潰れですから、今度はFoucaultの才能を妬み始めるのです。 | |
 | どうしようもない連中ですね。 | |
 | Foucaultは自分の実験の腕に自信がありましたし、また振り子実験や光速の測定だけでなく、ジャイロスコープの発明や写真技術の改良など、数々の業績を挙げていましたから、絶対にフランス科学アカデミーの会員になれると信じていました。ところが、何と専門家集団はあらゆる手を尽くしてそれを阻止し始めます。そのせいで、Foucaultはず~っと失業状態に置かれるのです。 | |
 | これは、単なるイジメですね。 | |
 | しかし、そこに救いの手が差し伸べられます。 | |
 | お。捨てる神あれば拾う神ありだ。 | |
 |
当時の皇帝Napolèon3世は科学技術大好き人間で、Foucaultの才能に大変な興味を示していました。
 Napolèon Ⅲ(1808~1873) それで、振り子実験の成功を耳にすると、パリ市民に広く知ってもらうために、パンテオンで公開実験することを命令し、最終的にフランス科学アカデミーに口添えまでしてくれることになります。  図1.5.45 パンテオン そのお陰でFoucaultはめでたく会員になることができましたとさ、おしまい。 |
|
 | で、光速の測定の話はどこへ行っちゃったんですか?? | |
 |
おっと、忘れるところでした。Foucaultが行った光速の測定も、Fizeauと同じように、光の行って帰っての時間計測に工夫を凝らすというものでした。具体的な実験装置は図1.5.46を見てください。
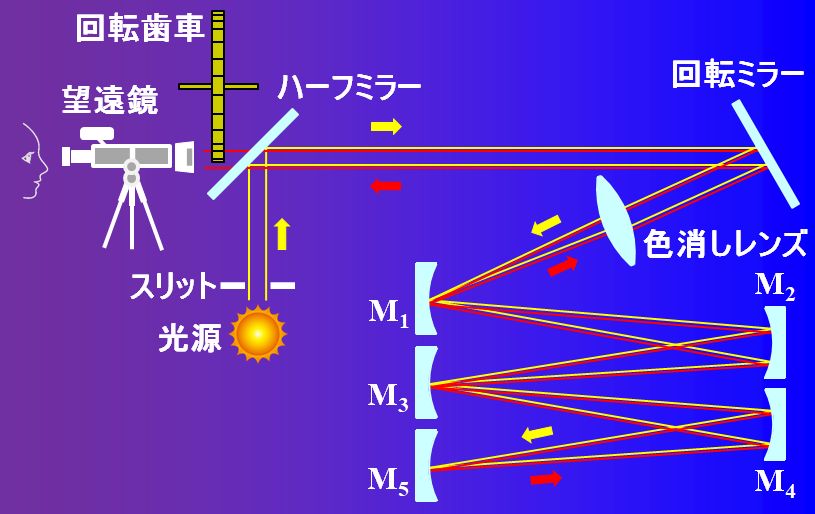 図1.5.46 Foucaultの方法 |
|
 | 回転歯車の代わりに回転ミラーを使うのか。 | |
 | この実験装置はFoucaultのアイデアの宝庫と言えるものです。まず、ラボで測定ができるということは、暗室環境を人工的に作れるので、光源として太陽光を用いることができます。これで、Fizeauの測定のときに懸案事項だった光量不足問題が解消されます。 | |
 | 確かに!! | |
 | この太陽光はスリットを通過後、ハーフミラーと回転ミラーで反射し、色消しレンズを透過します。太陽光はいろいろな波長が含まれていますが、少なくとも可視光については、色消しレンズの作用で同じ焦点を結ぶことができるようになります。 | |
 | なるほど!! | |
 | 色消しレンズを透過した光は、凹面鏡M1で結像し、そこで反射した後は発散しながら凹面鏡M2に向かいます。凹面鏡M2で反射した光は再び集光し、凹面鏡M3で結像します。同じことを繰り返して凹面鏡M5まで到達すると、そこで反射した光は元の光路で折り返してハーフミラーに到達します。 | |
 | わざわざ凹面鏡を使っているのはなぜですか?? | |
 |
この凹面鏡は曲率半径4mで作製されています。奇数番目の凹面鏡で結像するように5枚の凹面鏡をレイアウトすれば、それで正確に20mの光路を作ることができるんですよ。
 図1.5.47 論文抜粋(1) |
|
 | お~、考えましたね!! | |
 | そして、ハーフミラーに到達した光は、一部が透過して観測者の目に届きます。 | |
 | 教授。図1.5.46にも回転歯車っていうのがありますけど?? | |
 |
これもFoucaultのアイデアの1つですね。回転ミラーで反射した光は、その回転周期に応じて点滅しているように見えるはず。要するにストロボですね。このストロボ周期と回転歯車の回転周期が整数倍で同期すると、回転歯車はあたかも止まっているように見えるでしょ??
|
|
 | はいはい、よくダンス・パフォーマンスで見ますね。 | |
 |
回転歯車の方は小型軽量にしておいて、懐中時計と同じような原理でゆっくり回転させれば、非常に正確に回転速度を保つことができます。この回転歯車が止まって見えるように回転ミラーを制御することで、回転ミラーを高速で回転させても高い精度で回転速度を求めることができるわけです。これで、Fizeauの測定のときに懸案事項だった回転速度の精度問題が解消されます。
 図1.5.48 論文抜粋(2) (ストロボの原理が述べられている箇所) |
|
 | 頭いいなぁ。 | |
 |
さて、光が回転ミラーに入射した瞬間の様子が図1.5.49の(a)です。その後、光は距離\(l\)(=20m)を往復して回転ミラーに戻ってきます。しかし、この間に回転ミラーは\(\theta\)だけ回転しているので、反射した光は入射した光と別の光路を辿り、少しずれた(=\(d\))ところに到達します(b)。
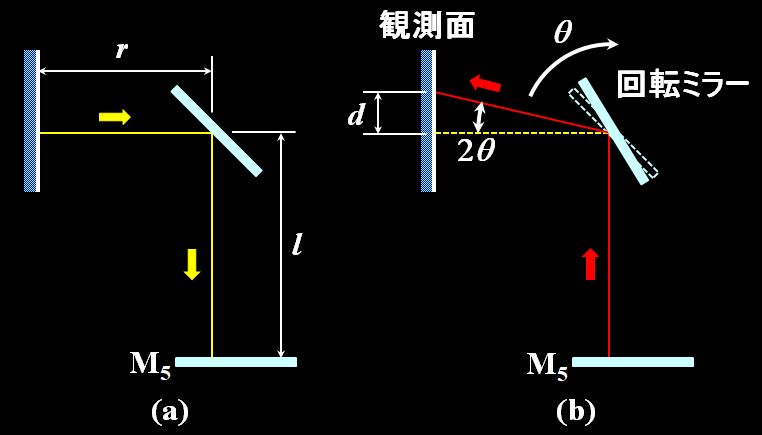 図1.5.49 回転ミラーと光路(余分な部品は省略した) 光の偏角は\(2\theta\)ですから、 \[ d = r \tan \left( 2 \theta \right) \approx 2 r \theta \quad \Leftrightarrow \quad \theta = \frac{ d }{ 2r } \tag{1.5.4} \] また、回転周波数を\(n\)とすれば、回転ミラーが\(\theta\)だけ傾くのに掛かる時間\(t\)は、 \[ t : \frac{1}{n} = \theta : 2 \pi \quad \Leftrightarrow \quad t = \frac{ \theta }{ 2 \pi n } \] 一方で、\(t\)は光の行って帰っての時間(=\(\cfrac{2l}{c}\))でもあるので、 \[ \frac{ 2 l }{c} = \frac{ \theta }{ 2 \pi n } \quad \Leftrightarrow \quad c = \frac{ 4 \pi n l }{ \theta } \tag{1.5.5} \] というわけで、式1.5.4を式1.5.5に代入すると、 \[ c = \frac{ 8 \pi n l r }{ d } \] ほら、論文と同じ式(論文)が導けました。  図1.5.50 論文抜粋(3) |
|
 | いよいよですねぇ。 | |
 |
\(n\)については、このような記載があります。
 図1.5.51 論文抜粋(4) 気を付けなければいけないのは、この回転ミラーは裏表の2面なので、実効的な周波数は2倍になるという点です。 |
|
 | つまり、\(n\)=800Hzってことか。 | |
 |
\(d\)については、\(d\)=0.7mmと記載されています。
 図1.5.52 論文抜粋(5) 残念ながら\(r\)の記載は論文中にはないのですが、\(r\)=0.52mとしましょう。従って―。 |
|
 |
えっと、 \(c\)= ( 8 × 3.14 × 800 Hz × 20 m × 0.52 m ) ÷ 0.7mm ≒ 2.98×108 m/s ですね。 |
|
 |
というわけで、論文と同じ数字が導けました。
 図1.5.53 論文抜粋(6) で、実際の光速\(c\)=299,792,458m/sと比較すると―。 |
|
 | お~、これは凄い。0.74%しか違わない!! | |
 | これは、当時の測定精度からすると驚異的な数値です。これこそFoucaultの実験センスの成せる業ですね。 | |
 | でも、Galileoからずいぶん時間が掛かりましたねぇ。 | |
 | そうですね。でも、人類の叡智がよく分かったんじゃないですか?? | |
 | 現在の数値は誰が決めたんですか?? | |
 |
1973年にEvensonが、レーザの波長と周波数を使って測定した数値(論文)をそのまま採用しているんです。
 Kenneth Melvin Evenson(1932~2002) 1983年の国際度量衡総会で、光速を基本定数にすることが決まったんですよ。 |
| 前頁へ | 戻る | 次頁へ |