 | Maxwellは、式1.4.8で光は電磁波であることを見破ったって話でしたけど、誰のデータに基づいて、そういう結論を出したんですか?? | |
 | Maxwellの論文が1864年に提出されているので、Fizeauのデータと比較したと言われてますね。さて、Maxwellは、真空中の光速\(c\)が不変定数だと主張したわけですが、これは当時の物理学会に対して真っ向勝負を挑む発言になります。 | |
 | 喧嘩上等!! | |
 | というのは、Maxwell方程式は、GalileoやNewtonの作り上げた古典力学の世界観と矛盾するからなんです。 | |
 | 矛盾?? | |
 |
例えば、50km/hで走る電車の中にいる人が140km/hでボールを投げたとしましょう。
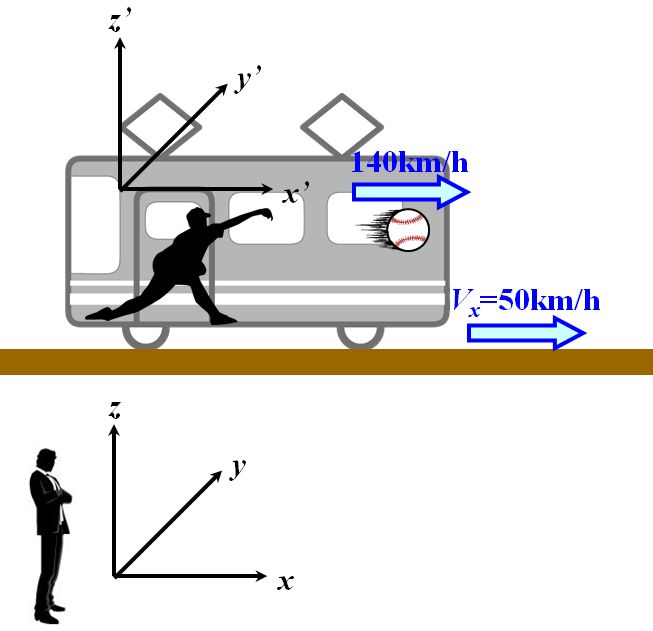 図1.6.1 Galilei変換 電車の外にいる人がこのボールを観測したら、その速さは?? |
|
 |
単純な足し算です。 50 km/h + 140 km/h = 190 km/h |
|
 | この速度の変換は、我々の感覚にも合ってますよね。この話を、もう少し格式高く表現すると、慣性系S\((x,y,z,t)\)に対し、速度\(V_x\)で運動している慣性系S'\((x^{\thinspace \prime},y^{\thinspace \prime},z^{\thinspace \prime},t^{\thinspace \prime})\)がある場合、慣性系Sと慣性系S'の間には次のような変換式が成立する、となります。 \[ x = x^{\thinspace \prime} + V_x t^{\thinspace \prime} \tag{1.6.1} \] \[ y = y^{\thinspace \prime} \tag{1.6.2} \] \[ z = z^{\thinspace \prime} \tag{1.6.3} \] \[ t = t^{\thinspace \prime} \tag{1.6.4} \] これをGalilei変換と言います。式1.6.1を時間で微分すると?? | |
 | こうですね。 \[ v_x = \frac{ dx }{ dt } = \frac{ dx }{ dt^{\thinspace \prime} } = \frac{ d }{ dt^{\thinspace \prime} } \left( x^{\thinspace \prime} + V_x t^{\thinspace \prime} \right) = \frac{ dx^{\thinspace \prime} }{ dt^{\thinspace \prime} } + V_x = {v_x}^{\thinspace \prime} + V_x \tag{1.6.5} \] なるほど。さっきの計算の一般式が出るわけですね。 | |
 |
このようなGalilei変換が成立するのが古典力学の世界観です。しかし、この問題を次のように変更してみましょう。光速で飛行するロケットにいる人が光を放出した場合、ロケットの外にいる人がこの光を観測したら、その速さは??
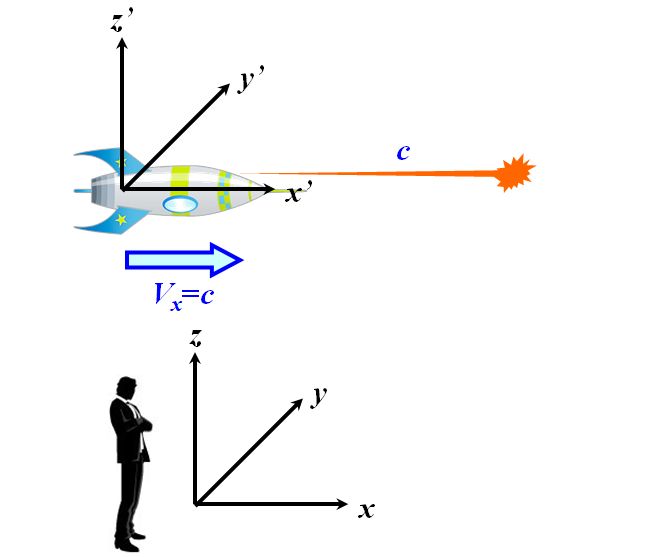 図1.6.2 Galilei変換、破れたり |
|
 |
単純な足し算です。 \(c + c = 2c\) |
|
 | そうはならない、というのがMaxwellの主張なんですよ。 | |
 | ムムム。光速は不変定数だからってこと?? | |
 | そうです。 | |
 | それはおかしいです。Maxwellが間違っているんですよ。 | |
 | はい。Maxwellの論文が提出されたとき、学会も同じ反応を示しました。「Maxwell方程式には不備がある」と受け止められたのです。とにかく、この頃のNewtonていうのは神様みたいな絶対的な存在でしたし、それに歯向かうような考え方を口にするなんて、早い話、愚か者なわけです。 | |
 | う~ん、愚か者っていうのはオーバーなような…。Maxwellって天才なんじゃなかったでしたっけ…。 | |
 |
しかし、若い人たちというのは発想が柔軟ですから、寧ろMaxwell方程式が正しくNewton方程式に不備があるのではないか、という見方が徐々に生まれてきます。そして、Maxwell方程式と矛盾しないようにNewton方程式を書き換えたらどうなるか、という視点で発表されたのが1905年のEinsteinの論文(論文)だったわけです。通称、特殊相対性理論と呼ばれているものですね。
 Albert Einstein(1879~1955) |
|
 | おぉ。そういうことなのかぁ。それでEinsteinはノーベル物理学賞をgetするわけですね。 | |
 | 違います。Einsteinがノーベル物理学賞を受賞するのは光電効果の理論的解明の方ですよ。 | |
 | あれ??そうでしたっけ?? | |
 |
はい。勘違いしている人、多いですけど。さて、次のようなことを考えてみましょう。速度\(V_x\)で運動している電車の中で、光を上から下へ放出させます。この電車の中に設置された時計で測ったとき、光が床に到達する時間を\(\Delta t^{\thinspace \prime}\)としましょう。
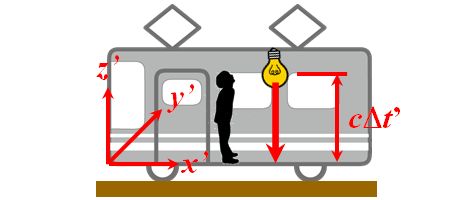 図1.6.3 電車の中で光を観測(慣性系S') 一方、この光を電車の外にある慣性系Sで観測すると、図1.6.4のように斜めの軌跡を描いているように見えるはずです。 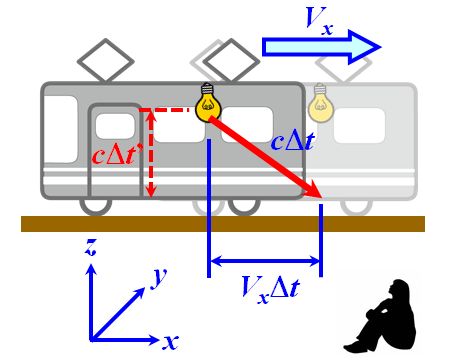 図1.6.4 電車の外から光を観測(慣性系S) |
|
 | そうですね。 | |
 | しかし、慣性系Sで観測している人にとっても、この軌跡を描いているのはあくまで光です。従って、その運動は光速\(c\)でなければなりません。Maxwellが主張していることは、そういうことです。 | |
 | なるほど。 | |
 | 慣性系Sに設置された時計で測ったとき、光が床に到達した時間を\(\Delta t\)としましょう。そうすると、次のようなPythagorasの定理が成立します。 \[ \left( c \Delta t \right)^2 = \left( V_x \Delta t \right)^2 + \left( c \Delta t^{\thinspace \prime} \right)^2 \] | |
 | ということは、 \[ \left( c \Delta t^{\thinspace \prime} \right)^2 = \left( c \Delta t \right)^2 - \left( V_x \Delta t \right)^2 = \left( c^2 - {V_x}^2 \right) \Delta t^2 \quad \Leftrightarrow \quad \Delta t^{\thinspace \prime 2} = \left[ 1 - \left( \frac{ V_x }{ c } \right)^2 \right] \Delta t^2 \] \[ \Leftrightarrow \quad \Delta t^{\thinspace \prime} = \Delta t \sqrt{ 1 - \left( \frac{ V_x }{ c } \right) ^2 } \tag{1.6.6} \] ですね。 | |
 | ルートの部分は\(1\)より小さいので\(\Delta t^{\thinspace \prime}< \Delta t\)ですが、これは何を意味しているかというと、慣性系Sに設置された時計で測った時間の進み方に対して、慣性系S'に設置された時計で測った時間はゆっくり進むということなのです。 | |
 | ん??ということは、光速に近い速度で動いている人は歳をとらないってこと?? | |
 | ではなくて、そういう人を慣性系Sで観測したら、歳のとり方がゆっくりに見える、ということです。 | |
 | あれ??ちょっと待って。その人から慣性系Sを見た場合、慣性系Sの方が光速に近い速度で動いているように見えませんか?? | |
 | そうですね。 | |
 | ということは、その人からすれば、慣性系Sにいる人の歳のとり方の方がゆっくり見えるってこと?? | |
 | はい。 | |
 | え~。だったら、どっちもどっちじゃないですか。 | |
 | 特殊相対性理論の「相対」っていうのは、つまり、そういうことなんですよ。 | |
 | 何か、特殊相対性理論って、つまんないですね。 | |
 | つまらないですか?? | |
 | だって、そんな「お互い様」の理論だったら、特殊相対性理論の正当性も証明しようがないじゃないですか。 | |
 | そんなことないですよ。特殊相対性理論が成立していることは、いくつかの事実によって証明されています。 | |
 | そうなんですか?? | |
 | はい。 | |
 | 例えば?? | |
 |
素粒子の1つにミュー粒子があります。これは、Andersonと、
 Carl David Anderson(1905~1991) Neddermeyerによって、1936年に宇宙線の中から観測されました(論文)。  Seth Henry Neddermeyer(1907~1988) ミュー粒子の静止しているときの平均寿命を初めて測定した(論文)のはRasettiですが、その後も何度もいろいろな人が繰り返して測定し、現在のところ2.2μsが標準的に使われる数値となっています(論文)。  Franco Dino Rasetti(1901~2001) |
|
 | 寿命が2.2μsしかないなんて、儚いですね。 | |
 | ところがですね。このミュー粒子が地球上で観測されるのは、ちょっと奇妙なんですよ。 | |
 | ん??なぜ?? | |
 | 仮に、ミュー粒子が光速で飛翔したとして、平均寿命の間に進む距離は、いくらですか?? | |
 |
それは簡単ですね。 3×108 m/s × 2.2×10-6 s = 6.6 × 102 m |
|
 |
つまり、660mしか進めません。ミュー粒子は、パイ中間子が、成層圏を構成している原子とぶつかって生成されます。成層圏は地表から10kmも上空にありますから、地表に到達することは殆どない、ということになります。
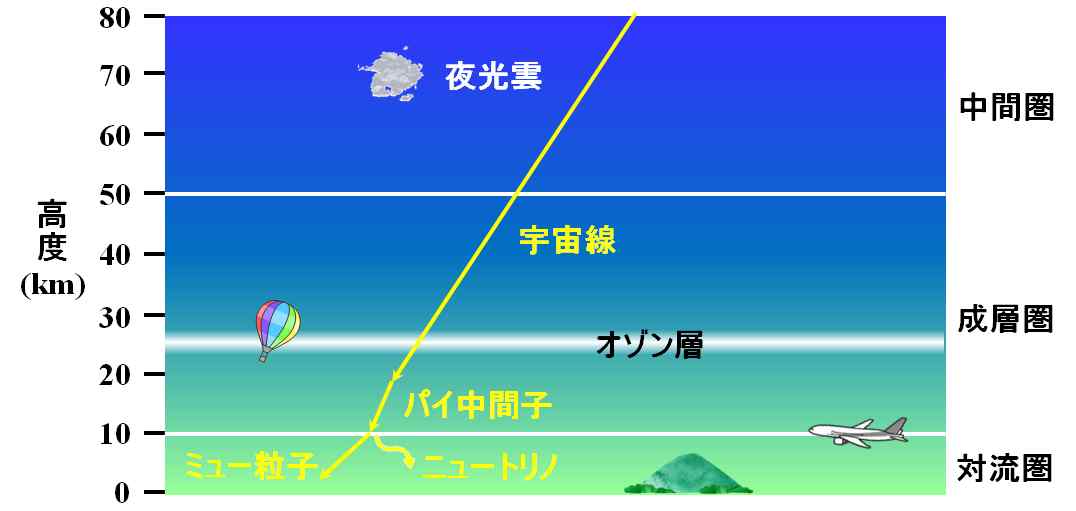 図1.6.5 ミュー粒子の生成 |
|
 | なるほど。 | |
 |
ところが、1963年に、Frischが行った正確な測定によると、ワシントン山で1時間あたり563±10個(6回の測定)、海面水準で1時間あたり408±9個(5回の測定)のミュー粒子が確認されました(論文)。
 David Henry Frisch(1918~1991) |
|
 | 結構、多いですね。 | |
 | また、シンチレーターに到達したときの運動エネルギーから、ミュー粒子の速度は、\(0.9950c\)と\(0.9954c\)の間であることも割り出しています。 | |
 | 光速には届かないけど、それでもかなり速いってことですね。 | |
 | 仮に、\(V_x=0.9950c\)として、地球から見たミュー粒子の寿命を計算してみましょう。 | |
 | それは、式1.6.6から、 \[ \Delta t = \cfrac{\Delta t^{\thinspace \prime}}{\sqrt{ 1 - \left( \cfrac{ V_x }{ c } \right) ^2 }} = \cfrac{2.2 \times 10^{-6}}{\sqrt{ 1 - \left( \cfrac{ 0.9950c }{ c } \right) ^2 }} = 2.2 \times 10^{-5} \] ですね。 | |
 | つまり、地球から見たミュー粒子は寿命が約10倍伸びるわけです。 | |
 | お~、そういうことか。いいじゃないですか。 | |
 | よって、先程は660mしか飛翔しなかったのが、約7kmも飛翔できることになるのです。 | |
 | 成層圏は10km上空だって言ってませんでしたっけ?? | |
 | 元気のいいパイ中間子は、もっと対流圏にまで潜り込んでミュー粒子を生成する可能性がありますし、そもそもここで言う平均寿命の定義というのは、「素粒子が崩壊することによって、その数が\(\cfrac{1}{\mathrm{e}}\)になるまでの時間」ですから、100個のミュー粒子があったとすると、37個は平均寿命よりも長生きするのです。 | |
 | 平均寿命って、半減期みたいなもの?? | |
 |
いえ。半減期は、粒子の数が文字どおり\(\cfrac{1}{2}\)になるまでの時間です。
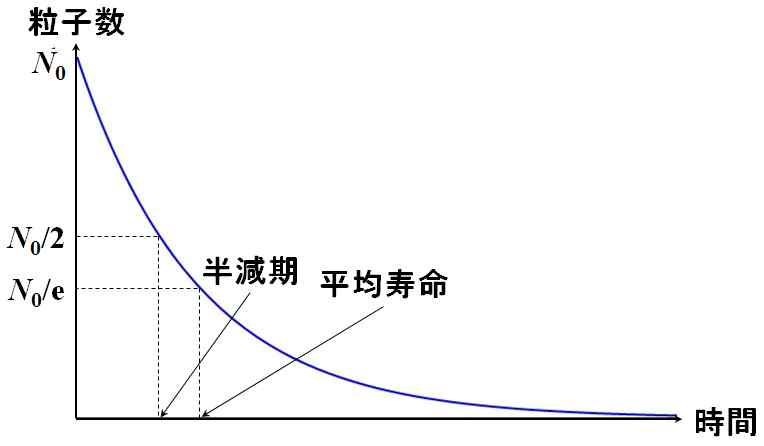 図1.6.6 平均寿命と半減期 |
|
 | 微妙に違うのか…。 | |
 | もし10km飛翔させたければ、平均寿命より約1.67倍以上も長生きするミュー粒子がいないといけませんが、それでも100個のうち約19個は存在します。よって、地上でカウントできても不思議はないですね。 | |
 | でも、今の話って、何だか違和感ありますね。 | |
 | そうですか?? | |
 | だって、ミュー粒子の立場になってみると、自分は2.2μsの寿命を全うしたと思っているわけじゃないですか。そうすると、結局、ミュー粒子は660mしか飛翔してない、って思ってますよ??何で、大気圏を突破できるんですか?? | |
 | なるほど。それについては、この後の議論で検証してみましょう。 | |
 | ひとまず、特殊相対性理論は正しい、だから、そのベースになっているMaxewllも正しい、ってことなのかな?? | |
 | 論理的にそうなるでしょう。となると、Newton方程式の方を修正しないといけない、ということになります。 | |
 | お、いよいよ権威の失墜ですね。 | |
 | いま見てきたように、慣性系によって時間が伸び縮みするということになると、物体の速度が、観測している慣性系によって異なるということになります。しかし、これでは何かと不都合なので、慣性系による不公平感を解消するために、速度\(\vec{\mathstrut v}\)で運動する物体に時計を持たせて、その時間\(\tau\)を使うということにしましょう。これを固有時間と言います。そうすると、この物体の運動量\(\vec{\mathstrut p}\)は、質量を\(m\)として、 \[ \vec{\mathstrut p } = m \frac{ d \vec{\mathstrut r} }{ d \tau } = m \frac{ d \vec{\mathstrut r} }{dt} \frac{ dt }{ d \tau } = m \vec{\mathstrut v } \frac{ dt }{ d \tau } \tag{1.6.7} \] と書けます。 | |
 | 式1.6.6が適用できるのでは?? | |
 | はい。\(\vec{\mathstrut v^2}=v^2\)ですから、 \[ d \tau = dt \sqrt{ 1 - \frac{ v^2 }{ c^2 } } \quad \Leftrightarrow \quad \frac { dt }{ d \tau } = \cfrac{ 1 }{ \sqrt{ 1 - \cfrac{v^2}{c^2} } } \] というわけで、式1.6.7は、\(\beta \equiv \cfrac{v}{c}\)として、 \[ \vec{\mathstrut p } = \cfrac{ m \vec{\mathstrut v} }{ \sqrt{ 1 - \beta^2 } } \tag{1.6.8} \] となりますね。 | |
 | そうすると、式1.3.5は、 \[ \vec{\mathstrut F } = \frac{ d }{ dt } \bigg( \cfrac{ m \vec{\mathstrut v} }{ \sqrt{ 1 - \beta^2 } } \bigg) \] に変更されるのかぁ。 | |
 | これが、相対論的運動方程式になります。また、 \[ \frac{ 1 - \beta^2 }{ 1 - \beta^2 } = 1 \] という恒等式が成立しますが、この両辺に\((mc^2)^2\)を掛けると、 \[ \frac{ \left( m c^2 \right)^2 }{ 1 - \beta^2 } - \frac{ \left( m c^2 \right)^2 \beta^2 }{ 1 - \beta^2 } = \left( m c^2 \right)^2 \] この左辺の第2項は、式1.6.8を使うと、\(\vec{\mathstrut p^2}=p^2\)ですから、 \[ \frac{ \left( m c^2 \right)^2 \beta^2 }{ 1 - \beta^2 } = \frac{ m^2 c^4 \beta^2 }{ 1 - \beta^2 } = c^2 \frac{ m^2 c^2 \beta^2 }{ 1 - \beta^2 } = c^2 \frac{ m^2 \left( c \beta \right)^2 }{ 1 - \beta^2 } = c^2 \frac{ m^2 v^2 }{ 1 - \beta^2 } = c^2 p^2 = \left( cp \right)^2 \] ですね。更に、左辺の第1項については、 \[ E \equiv \frac{ m c^2 }{ \sqrt{ 1 - \beta^2 } } \] という相対論的エネルギー\(E\)を定義します。 | |
 | てことは、 \[ E^2 - \left( cp \right)^2 = \left( m c^2 \right)^2 \] ってこと?? | |
 | はい。これ、どっかで見たことないですか?? | |
 | う~ん、記憶に…ない…かも…。 | |
 | 少し変形しましょうか。 \[ E^2 = \left( cp \right)^2 + \left( m c^2 \right)^2 \quad \Leftrightarrow \quad E = \sqrt{ \left( cp \right)^2 + \left( m c^2 \right)^2 } \tag{1.1.16} \] これで思い出せるのでは??前にやった相対論的な運動量とエネルギーの関係です。 | |
 | 朧げながら、記憶が戻って…きた…かも…。 | |
 | いずれにせよ、Maxwell方程式がなければ時空に関する反省はなかっただろうし、Einsteinが特殊相対理論を提出することもなかったってことです。そういう意味で、Maxwell方程式は20世紀の物理学の足掛かりとして非常に重要な位置にあると言えるんですよ。 | |
 | で、Galilei変換はどう修正されるんですか?? | |
 | それに対応するLorentz変換という変換式が用意されています。 \[ x^{\thinspace \prime} = \frac{ x - V_x t }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } \tag{1.6.9} \] \[ y^{\thinspace \prime} = y \tag{1.6.10} \] \[ z^{\thinspace \prime} = z \tag{1.6.11} \] \[ t^{\thinspace \prime} = \frac{ t-\left( \cfrac{V_x}{c^2} \right) x }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } \tag{1.6.12} \] | |
 | Galilei変換からLorentz変換へ様変わりかぁ。 | |
 | では、先程やり残した議論を片づけますか。 | |
 | ミュー粒子の立場になった場合の話ですね。 | |
 | そこで、慣性系Sの\(x\)座標に沿って置かれた、1本の棒を考えます。この両端の座標を\(x_1\)、\(x_2\)とすると、棒の長さ\(L_0\)は、 \[ L_0 = x_2 - x_1 \tag{1.6.13} \] です。 | |
 | 当然ですね。 | |
 | さて、この棒を慣性系S'で見た場合にどうなるか、が問題です。 | |
 | 式1.6.9を使えばいいのでは?? | |
 | それではダメですね。 | |
 | え、何で?? | |
 | おそらく、 \[ x = x^{\thinspace \prime} \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } + V_x t \] ということをイメージしているのでしょうが、右辺には慣性系Sと慣性系S'のパラメータが混在しているでしょう?? | |
 | う~ん。確かに…。 | |
 | というわけで、式1.6.9と式1.6.12をまとめて処理することを考えないといけません。 | |
 | \(x\)と\(t\)を\(x^{\thinspace \prime}\)と\(t^{\thinspace \prime}\)に変換するのが式1.6.9と式1.6.12だから、その逆か…。あ、行列で考えればいいのでは?? | |
 | そうですね。 \[ \left( \begin{array}{c} x^{\thinspace \prime} \\ t^{\thinspace \prime} \end{array} \right) = \frac{ 1 }{ \sqrt{1-\left(\cfrac{V_x}{c}\right)^2} } \left( \begin{array}{cc} 1 & -V_x\\ -\cfrac{V_x}{c^2} & 1 \end{array} \right) \left( \begin{array}{c} x \\ t \end{array} \right) \] と整理しておくと見通しがよさそうです。 | |
 | この行列の行列式は、 \[ \frac{ 1 }{ \sqrt{1-\left(\cfrac{V_x}{c}\right)^2} } \left( 1 - V_x \times \cfrac{V_x}{c^2} \right) = \frac{ 1-\left(\cfrac{V_x}{c}\right)^2 }{ \sqrt{1-\left(\cfrac{V_x}{c}\right)^2} } = \sqrt{1-\left(\cfrac{V_x}{c}\right)^2} \] だから、逆行列は、 \[ \frac{ 1 }{ \sqrt{1-\left(\cfrac{V_x}{c}\right)^2} } \left( \begin{array}{cc} 1 & V_x\\ \cfrac{V_x}{c^2} & 1 \end{array} \right) \] ですね。 | |
 | つまり、 \[ \left( \begin{array}{c} x \\ t \end{array} \right) = \frac{ 1 }{ \sqrt{1-\left(\cfrac{V_x}{c}\right)^2} } \left( \begin{array}{cc} 1 & V_x\\ \cfrac{V_x}{c^2} & 1 \end{array} \right) \left( \begin{array}{c} x^{\thinspace \prime} \\ t^{\thinspace \prime} \end{array} \right) \] ですから、 \[ x = \frac{ x^{\thinspace \prime} + V_x t^{\thinspace \prime} }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } \tag{1.6.14} \] \[ t = \frac{ t^{\thinspace \prime} + \cfrac{V_x}{c^2} x^{\thinspace \prime} }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } \tag{1.6.15} \] を用いる必要があるわけです。 | |
 | そうすると、 \[ \begin{align*} L_0 &= x_2 - x_1 = \frac{ {x_2}^{\thinspace \prime} + V_x {t_2}^{\thinspace \prime} }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } - \frac{ {x_1}^{\thinspace \prime} + V_x {t_1}^{\thinspace \prime} }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } \\ &= \frac{ {x_2}^{\thinspace \prime} - {x_1}^{\thinspace \prime} }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } - V_x \frac{ {t_2}^{\thinspace \prime}- {t_1}^{\thinspace \prime} }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } \tag{1.6.16} \end{align*} \] になります。 | |
 | ここで吟味しなければならないのは、慣性系S'における長さとは何か、という問題です。 | |
 | 何だか、哲学めいてますね。 | |
 | 長さを測るとき、\({x_1}^{\thinspace \prime}\)と\({x_2}^{\thinspace \prime}\)の座標は、慣性系S'において同時刻で決められたものでなければ意味がありません。 | |
 | う~ん。言われれば、確かにそうですね。 | |
 | よって、式1.6.16において、\({t_1}^{\thinspace \prime}={t_2}^{\thinspace \prime}\)としたときに、慣性系S'から見た棒の長さ\(L\)が決まるのです。 | |
 | ひょっとして、 \[ L_0 = \frac{ {x_2}^{\thinspace \prime} - {x_1}^{\thinspace \prime} }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } = \frac{ L }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } \tag{1.6.17} \] ってこと?? | |
 |
はい。ルートの部分は\(1\)より小さいので\(L < L_0\)ですから、慣性系S'からは、棒の長さは縮んでいるように見えるということなのです。これをLorentz-Fitzgerald収縮と言います。
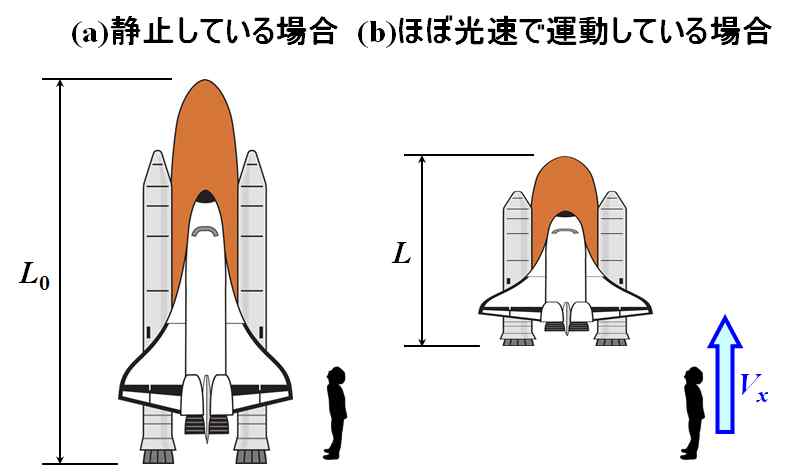 図1.6.7 Lorentz-Fitzgerald収縮 |
|
 | お、痩せているように見せることができるってこと??いいじゃないですか~。 | |
 | 相手に光速で走ってもらわないといけませんけど。それなら、真面目にダイエットした方が現実的です。 | |
 | 教授は、本当に夢がないですね。 | |
 | …。さて、ここまで来ると、ミュー粒子の立場が理解できませんか?? | |
 | あ、忘れてた。 | |
 | ミュー粒子が光速で地球に近づいているわけですから、大気圏の厚さは―。 | |
 | 進行方向に縮んでいるように見えているわけか!!だから、2.2μsの寿命を全うしたときに、大気圏を突き抜けてもおかしくない、ということなんですね。 | |
 | そういうことです。 | |
 | 産まれてから死ぬまで動きまわっているミュー粒子にしてみると、Lorentz-Fitzgerald収縮が起こっているのかどうか、知りようがないですね。 | |
 | 静止したときの長さを知って初めて、運動したときにLorentz-Fitzgerald収縮が起こったと認識できるはずなので、そのとおりでしょう。 | |
 | 現象はお互い様でも、特殊相対性理論が証明できる、ということは分かりました。 | |
 | ついでに、Lorentz変換に従う速度合成則を導いてみましょう。まず、式1.6.9から、 \[ dx^{\thinspace \prime} = \frac{ dx - V_x dt }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } \] また、式1.6.12から、 \[ dt^{\thinspace \prime} = \frac{ dt - \cfrac{V_x}{c^2} dx }{ \sqrt{ 1 - \left( \cfrac{V_x}{c} \right)^2 } } \] なので、両辺を割ってください。 | |
 | これは…。ん~と、 \[ {v^{\thinspace \prime}}_x = \frac{ dx^{\thinspace \prime}}{ dt^{\thinspace \prime} } = \frac{ dx - V_x dt }{ dt - \cfrac{V_x}{c^2} dx } = \frac{ v_x - V_x }{ 1 - \cfrac{V_x}{c^2} v_x } \tag{1.6.18} \] かな。式1.6.5とはずいぶん違いますね。 | |
 | しかし、式1.6.18で\(V_x\)が\(c\)に比べてとても小さいと、分母は\(1\)に近似できるので、 \[ {v^{\thinspace \prime}}_x \approx v_x - V_x \] となり、式1.6.5が導かれます。 | |
 | なるほど。図1.6.2だと、\({v^{\thinspace \prime}}_x=V_x=c\)だから、 \[ c = \frac{ v_x - c }{ 1 -\left( \cfrac{c}{c^2} v_x \right) } = \frac{ v_x - c }{ 1 -\left( \cfrac{v_x}{c} \right) } \quad \Leftrightarrow \quad c - v_x = v_x - c \quad \Leftrightarrow \quad v_x = c \] か…。お~、慣性系Sでも、放出した光は光速\(c\)で見えるってことかぁ。 | |
 |
つまり、Lorentz変換の下であれば、Maxwellの主張に矛盾が生じない(論文)わけです。
 Hendrik Antoon Lorentz(1853~1928) |
|
 | ときどき、Einsteinの相対性理論は間違っている、って主張する人がいますよね?? | |
 | いますね。 | |
 | それについて、教授はどう考えているんですか?? | |
 | そういう主張には2種類あると思います。1つは、本気で間違っていると主張している人たちですね。 | |
 | 本まで出版してますけど?? | |
 | そういう主張の多くは勘違いですね。基本的な数式が間違ってたりしますから、読むだけ無駄です。 | |
 | もう1つは?? | |
 | Einsteinとは別の理論で説明できる、という主張です。 | |
 | それについては?? | |
 |
物理学でやっていることは、人間が自然を理解するためのモデルの構築です。だから、上手く説明できるモデルだったら何でもいいんですよ。重要なのは、 ①そのモデルで、既知の現象が充分に説明できること ②そのモデルを数式で記述できること ③そのモデルから新しい現象を予言できること ④その予言を実験的に証明できること が満たされることです。 |
|
 | Einsteinのモデルは、それができている?? | |
 | はい。しかし、Einsteinとは別の理論で説明できると主張している人たちの中で、少なくとも③と④に発展させた学説を見たことがありません。また、①や②についても、あえてその人たちの理論を採用しようとは思えませんし。 | |
 | なぜですか?? | |
 |
エレガントでないからです。次から次へ辻褄合わせをする理論は、たとえ整合性があったとしても美しくありません。しかし、Einsteinの理論は、 1.自然法則はすべての慣性系において同等である。 2.真空中において、光の速度は光源の速度に依らず一定である。 という2つの公理を認めさえすれば、あらゆることが説明できます。 |
|
 | これ以上、何も望むものがないってことですね。 | |
 | そういうことです。 |
| 前頁へ | 戻る | 次頁へ |