 | 新しい章に突入ですね。 | |
 |
光は粒子か波動か、という論争は非常に長い間、物理学会の未解決問題だったわけですが、いち早く光の波動説を唱えたのはHookeです。
 Robert Hooke(1635〜1703) |
|
 | Hookeの法則の?? | |
 | そうです。Hookeは大変に優れた実験家で、 Newtonよりも早くいろいろな法則を見出していたんですが、いかんせん数学の力が不足していました。 | |
 | その点はFaradayとよく似てますね。 | |
 | Hookeの不幸だったのは、少し遅れて王立協会の会員になったNewtonがプライドの塊のような人物だった、という点でしょう。そのうえ、数学の天才で、数々の法則を体系的な理論にまとめ上げてしまうと、殆どの成果はNewtonの手柄という風潮が定着してしまうのです。 | |
 | でも、それならHookeが黙ってないでしょう?? | |
 | ですから、この2人は始終論争を巻き起こしていました。そして、Hookeが先に亡くなると、Newtonは徹底的にHookeの業績を抹殺することに奔走するわけです。 | |
 | 酷いですね〜。 | |
 | Hookeの肖像画も残さないという徹底ぶりだったようですね。 | |
 | ん??すると、上の人物画は?? | |
 | 想像画ですよ。いずれにしても、Newtonが学会に君臨することにより、光の粒子説が主流となるのです。ただ、Newton自身は、光の正体が粒子なのか波動なのかという問題については慎重に考えていて、自分の意見を結構コロコロ変えています。Newtonが生きていた時代に明らかになっていた光の性質を上手く説明できるのは粒子の方だと考察を進めていったのは間違いないのですが、これを"粒子説"として固めたのは、どちらかと言うとNewton信奉者なのです。 | |
 | そう言えば、クラシック音楽でもBrahmsとWagnerの仲が悪かったってよく言われるけど、実際はBrahms派と呼ばれる保守派と、Wagner派と呼ばれる急進派の派閥闘争だって言われてますね。 | |
 |
同じようなイメージですね。ところが、その論争に止めを刺す発見がもたらされます。それが干渉という現象ですね。Youngによって発見され(論文)ました。
 Thomas Young(1773〜1829) |
|
 | Youngって、弾性力学を勉強するとYoung率って出てくるけど、その人ですか?? | |
 | そうです。Youngの専門は医者でして、網膜の研究と絡めて光の解明に尽力しました。14歳で8ヶ国語を話せたという語学の達人でもあります。 | |
 | 8ヶ国語??私、日本語しか話せないですよ…。 | |
 |
Napolèonがエジプト遠征で持ち帰ったロゼッタ・ストーンて知ってますか??
 図3.1.1 ロゼッタ・ストーン |
|
 | ヒエログリフ?? | |
 |
はい。それを解読したのは、一般にはChampollionと言われてますが、実はYoungも語学が堪能であったということから、大きな貢献をしています。
 Jean-François Champollion(1790〜1832) ですから、どちらが解読への貢献度が大きかったのかという問題は、いまだにイギリスとフランスの間で論争の種になっているようです。 |
|
 | そういう論争は平和でいいですね。 | |
 | さて、実はYoungが波動説を唱えたとき、物理学会は、それでも尚、粒子説に固執していて、干渉だとか、後で説明する回折といった現象をどうにか粒子説で説明できないか、ということに躍起になっていました。 | |
 | え〜、さすがにそれは無理があるような…。 | |
 | そこで、LaplaceとかBiotといった物理学者たちによって構成されていたフランス科学アカデミーは、とうとう懸賞金を掛けるまでになります。その懸賞問題に論文投稿したのがFresnelだったんですね。 | |
 | へぇ、あの冴えない顔をした人ですね。 | |
 | ところが、Fresnelの論文はフランス科学アカデミーの思惑とは真っ向勝負を挑むもので、寧ろ波動説で光の直進性や反射、屈折が説明でき、しかも回折や干渉などにも展開できる、ということを証明したものでした。 | |
 | お、なかなか、やりますね〜。 | |
 |
そこで、その審査員だったPoissonがFresnel理論の反証として、ある実験を思い付きます。
 Siméon Denis Poisson(1781〜1840) |
|
 | こうなってくると、もはや果たし合いみたいですね。 | |
 |
Poissonの主張は、「もし、Fresnelの理論が正しければ、光源の後ろに球状の障害物があったとしても、光はその障害物をまわり込んで干渉するから、障害物の影の中心部に明るい点ができるはずだ」というものでした。
左側にあるスクリーンに、照明の当たったコインの像が映りますが、その中心に明るい点ができていることが分かりますね?? |
|
 | う〜ん。だったら、同じような実験で確認すれば済む話ですよね。 | |
 | Poissonがこの実験を反証に持ってきたのは、これが日常では観測されないことを知っていたからですよ。これを当時の実験技術で再現するのは無理難題だったのです。 | |
 | 意地悪ですね。そんなの、かぐや姫の要求した宝物みたいなものじゃないですか。 | |
 |
ところが、アカデミーの委員長を務めていたAragoが見事、実験でPoissonの主張を証明(論文)してしまうのです。
 Dominique François Jean Arago(1786〜1853) そのため、この点はAragoスポットと呼ばれますね。これで、いよいよPoissonも波動説に鞍替えせざるを得なくなり、光の波動説が一気に主流になっていくのです。 |
|
 | どうして、Aragoは一肌脱ぐことにしたのかな?? | |
 | AragoはFresnelの共同研究者で、フランス科学アカデミーの懸賞問題に論文投稿するようFresnelをけしかけた張本人だからですよ。 | |
 | 共犯者か〜。そう言えば、この人ってFizeauの実験のときにも登場してましたね。 | |
 | 知らない人が多いんですが、Arago家っていうのは、フランスの政治において必ず主要メンバーに入っているくらいの名門中の名門です。この人も、最終的には首相にまで上り詰めるんですが、若い頃は数学と物理学に興味を示し、そちらでも優れた才能を発揮させました。 | |
 | 政治に物理に、凄いな…。 | |
 |
そして、Laplaceに認められて、パリ子午線の測量メンバーに選出されます。
 Pierre-Simon Laplace(1749〜1827) これは、1メートルを定義するための重要な測量だったんですが、不幸なことにスペインで測量中、祖国フランスがスペインと戦争を始めて、スパイ容疑で捕虜になってしまいます。 |
|
 | お〜。 | |
 | 更に、脱走に成功したのに、マルセイユ行きの船が難破して、スペインよりも性質の悪いイスラム教徒に捕まってしまいます。 | |
 | シンドバッドの冒険みたいですね…。波乱万丈…。 | |
 | ところが、Aragoは機転を利かせてイスラム教へ改宗し、紆余曲折を経て、3年後フランスに戻ることに成功します。 | |
 | それにしても強運の持ち主ですねぇ。 | |
 | ラッキーだったのは、測量結果が奇跡的に無事だったことで、そのためAragoはたちまち有名人になり、いろいろな団体の重要メンバーを兼任することになるのです。 | |
 | お〜、英雄だ。 | |
 | が、そのお陰で、Aragoは科学技術へ直接関わることができなくなってしまいます。特に、光速の高精度の測定は、航海技術に重要だったため、Aragoは高い関心を寄せていたわけですが、そこで白羽の矢を立てたのが、 FizeauとFoucaultだったというわけです。 | |
 | なるほど〜。 | |
 | こうしてみると、Aragoは、光に関していろいろな人たちに影響を与え、その進歩を促したポジションにいたことが分かりますね。 | |
 | 明治維新の坂本龍馬みたいな感じですね。 |
〜干渉の基本〜
 |
さて、波動の干渉は、このような現象です。
|
|
 | 光の性質としては有名な現象ですけど、日常では殆ど見掛けないですね。 | |
 | そうですね。蛍光灯の光が干渉して、床がまだら模様に見えるということはありません。 | |
 | どうしてですか?? | |
 | 光の干渉は、同一光源を分割して合成するという手続きを踏まないと、殆ど観測することができないからです。 | |
 | お風呂でチャプチャプ波紋を発生させたり、音波の場合だと干渉って簡単に観察できますけど?? | |
 | それは、波長のレベルがまったく違うからですね。可視光だと数100nm程度なので、目視で干渉を観察するのが格段に難しくなるんですよ。 | |
 | なるほど。 | |
 | さて、干渉は2つの波動の重ね合わせで生じるので、 \[ \left\{ \ \begin{array}{l} E_1 = A_1 \exp \big[ i \left( k_1 x -\omega_1 t + \phi_1 \right) \big] \\ E_2 = A_2 \exp \big[ i \left( k_2 x -\omega_2 t + \phi_2 \right) \big] \end{array} \right. \] という2つの波動を合成し、\(x=0\)で観察したことを考えてみましょう。そのときの強度\(I\left(t\right)\)はどうなりますか?? | |
 | いきなり強度かぁ。 \[ \begin{align*} I \left( t \right) &= \left| E_1 + E_2 \right|^2 \\ &= \left| E_1 \right|^2 + E_1 {E_2}^{*} + {E_1}^{*} E_2 + \left| E_2 \right|^2 \\ &= {A_1}^2 + {A_2}^2 + A_1 A_2 \mathrm{e}^{ i \big[ \left( \omega_2 - \omega_1 \right) t - \left( \phi_2 - \phi_1 \right) \big] } + A_1 A_2 \mathrm{e}^{ - i \big[ \left( \omega_2 - \omega_1 \right) t - \left( \phi_2 - \phi_1 \right) \big] } \\ &= {A_1}^2 + {A_2}^2 + 2 A_1 A_2 \cos \big[ \left( \omega_2 - \omega_1 \right) t - \left( \phi_2 - \phi_1 \right) \big] \end{align*} \] かな…。 | |
 | 実際は、検知されるエネルギーは有限時間内での時間平均なので、 \[ I = \langle I \left( t \right) \rangle = \frac{1}{T_0} \int_0^{T_0} I \left( t \right) \] \[ \phantom{I} = {A_1}^2 + {A_2}^2 + 2 A_1 A_2 \langle \cos \big[ \left( \omega_2 - \omega_1 \right) t - \left( \phi_2 - \phi_1 \right) \big] \rangle \tag{3.1.1} \] とするべきでしょう。 | |
 | < >は?? | |
 | 有限時間\(T_0\)内における平均を表します。式3.1.1の右辺の第1項と第2項は、2つの波動がそれぞれ単独で存在したときの強度であり、第3項は干渉項と呼ばれています。 | |
 | 干渉によって出現した新しい項ってことですね。 | |
 | 干渉項を分析することで、いくつかのケースに整理することができます。そこで、干渉項の第1項を、 \[ \left( \omega_2 - \omega_1 \right) t = \left( \frac{2 \pi}{T_2} - \frac{2 \pi}{T_1} \right) t = 2 \pi \left( \nu_2 - \nu_1 \right) t \] と変形しておきましょう。 | |
 | \(\nu\)は周波数でしたっけ…。 | |
 | そうです。周波数の差はビート現象を意味します。 | |
 | でも、実際にビート現象が生じるときって、2つの周波数の差は小さくないといけないですよね?? | |
 | もう少し厳密に言うと、 \[ \frac{1}{\nu_2 - \nu_1} \leq T_0 \tag{3.1.2} \] の条件では、ビート現象は生じません。そして、このとき干渉項は\(0\)になるので、干渉を観察することができないわけです。 | |
 | 式3.1.2の条件から外れると、ビート現象が観察できるわけですね。 | |
 | そのような干渉はヘテロダイン干渉と言いますが、ただ、これを観察しようとすると、それなりの方法を用いないと難しいです。今回は、ヘテロダイン干渉には立ち入りません。 | |
 | \(\omega_2-\omega_1=0\)という条件でもビート現象が消える気がするんですけど。 | |
 | そのときは、式3.1.1が、 \[ I = {A_1}^2 + {A_2}^2 + 2 A_1 A_2 \langle \cos \big[ \left( \phi_1 - \phi_2 \right) \big] \rangle \tag{3.1.3} \] と書けます。このような干渉をホモダイン干渉と言います。通常は、式3.1.3の干渉項が一定値になるケースを議論の対象にしますね。その場合は、 \[ \langle \cos \big[ \left( \phi_1 - \phi_2 \right) \big] \rangle = \cos \big[ \left( \phi_1 - \phi_2 \right) \big] \] なので、議論の見通しがよくなります。 | |
 | 位相の差によって\(I\)が変化するわけか。 | |
 |
例えば、図3.1.2のように2つの光源P1、P2があって、観測点をQとしたとき、それぞれの光路長の差\(\overline{{\rm P}_1{\rm Q}}-\overline{{\rm P}_2{\rm Q}}\)から位相差を求めることで、その観測点における強度\(I\)が分かります。
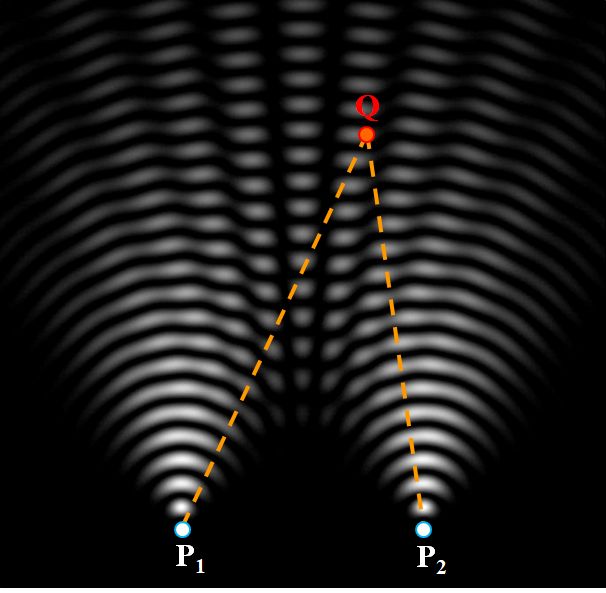 図3.1.2 干渉 |
|
 | そうすると、\(m\)を整数(=次数)として、 \[ \left( 2m - \frac{1}{2} \right) \pi < \phi_1 - \phi_2 < \left( 2m + \frac{1}{2} \right) \pi \tag{3.1.4} \] が強め合う条件で、 \[ \left( 2m + \frac{1}{2} \right) \pi < \phi_1 - \phi_2 < \left( 2m + \frac{3}{2} \right) \pi \tag{3.1.5} \] が弱め合う条件になりますね。 | |
 | 更に、 \[ \phi_1 - \phi_2 = 2m \pi \tag{3.1.6} \] が\(I_{max}\)条件で、 \[ \phi_1 - \phi_2 = \left( 2m + 1 \right) \pi \tag{3.1.7} \] が\(I_{min}\)条件になります。以上が、光が干渉すると図3.1.2のように、まだら模様に見える理由です。 |
| 前頁へ | 戻る | 次頁へ |