 | ここまで複屈折について見てきましたが、これは結晶の持つ特有の性質として発現するだけでなく、等方性媒質でも圧力を与えることで生じることがあります。 | |||||||||||||||||||||||||||||
 | 応力複屈折ですね。 | |||||||||||||||||||||||||||||
 | 応力複屈折については以前触れましたが、光路長差を\(\Delta l\)とし、媒質の厚み\(d\)、歪みの大きさ(応力)\(F\)、光弾性係数\(\beta\)を使って、 \[ \Delta l = d \times F \times \beta \tag{2.9.1} \] と定式化できました。 | |||||||||||||||||||||||||||||
 | そうでしたね。 | |||||||||||||||||||||||||||||
 |
そうすると、例えばプラスチックでレンズを成型した場合、いろいろと問題が発生しそうだな、ということが予想されます。樹脂レンズは、ペレット状になったプラスチック材料を、スクリューで型に送り込む過程でヒーターにより溶融し、何tという圧力をかけて型に流し込んだ後、それを冷やして取り出すというプロセスで成型されます。
|
|||||||||||||||||||||||||||||
 | 何か、いかにも歪みが発生しそうな方式ですね。 | |||||||||||||||||||||||||||||
 | 特に、プラスチックを使ってレンズを成型するのは、レンズ面が複雑な形状をしていてガラスでの研磨加工ができないのが理由ですから、そもそも型内部の圧力を均等にすることが難しいのです。そうすると、圧力のムラが発生し、好ましくない歪みを生み出すことになります。 | |||||||||||||||||||||||||||||
 | でも、式2.9.1を見ると、\(\Delta l\)を小さくするパラメータは3つしかないですよね。\(F\)の制御は難しいし、\(d\)はレンズ設計で決まっちゃうのでは?? | |||||||||||||||||||||||||||||
 |
そうですね。だから、光弾性係数の小さい材料を選定することがセオリーになります。しかし、樹脂レンズに適用できる材料は非常に限られていて、アクリル(PMMA)、ポリカーボネート(PC)、シクロオレフィン樹脂(CO)の3つしかありません。
|
|||||||||||||||||||||||||||||
 | 3つ??たった?? | |||||||||||||||||||||||||||||
 | 厳密には、樹脂は大きく熱可塑性樹脂、熱硬化性樹脂、光硬化性樹脂の3つに分けられますが、複写機などのLSUに利用されるような高精度のレンズには熱可塑性樹脂しか使うことができず、その中でも3つしかない、と言うべきでしょう。 | |||||||||||||||||||||||||||||
 | なぜですか?? | |||||||||||||||||||||||||||||
 | まず、光硬化性樹脂は、その用途がほぼ接着剤に限定されます。最近では、3Dプリンターの材料で使われることもありますが、レンズの候補にはなり得ませんね。 | |||||||||||||||||||||||||||||
 | 眼鏡レンズの材料は熱硬化性樹脂じゃなかったでしたっけ?? | |||||||||||||||||||||||||||||
 | そうです。熱硬化性樹脂は、一般に流動性を有する低分子の状態で存在しており、ある温度以上に加熱されると、低分子同士が架橋反応により高分子の立体網目状構造へと材質の構造変化を引き起こし硬化します。ところが、架橋反応による体積収縮が大きく、熱可塑性樹脂よりも成型収縮率が高い。このため、高精度なレンズを成型することが難しく、また成型時間が長いというのも課題となります。要するに、量産性が極端に悪くなるんです。 | |||||||||||||||||||||||||||||
 | 眼鏡レンズは一点ものだから量産性は気にしなくていいってことか。でも、精度については、どうなっているんですか?? | |||||||||||||||||||||||||||||
 | 人間の脳の補正能力が高いので、そこそこの精度でも実用上は問題ないんですよ。 | |||||||||||||||||||||||||||||
 | へぇ、人間の脳って優秀なんですね。 | |||||||||||||||||||||||||||||
 | 熱可塑性樹脂は結晶性樹脂と非晶性樹脂に大別できますが、レンズに使えるのは非晶性樹脂のみです。 | |||||||||||||||||||||||||||||
 | 結晶化すると透明じゃなくなるからですね。 | |||||||||||||||||||||||||||||
 | 実用的には耐久性も考えないといけませんし、そうやって高精度レンズに求められる制約を満たす材料という具合に絞り込んでいくと、結果としてと3つしか残らない、ということなんですよ。 | |||||||||||||||||||||||||||||
 | 教授。表を見ると、PCはやたらに光弾性係数が高くないですか?? | |||||||||||||||||||||||||||||
 | そうですね。ところが、シクロオレフィン樹脂が登場するまではPC以外に適当な材料がなく、そのため生産区はPCの応力複屈折をいかに低減するか、という取り組みに大変苦労したという話を聞いたことがあります。その中で注目に値する技術としてゲートシール法がありますね。 | |||||||||||||||||||||||||||||
 | ゲート??シール?? | |||||||||||||||||||||||||||||
 |
ゲートというのは、レンズに樹脂を流し込む入り口のことですが、その入り口に小さな部屋を作っておいて、金属のボールを入れておきます(図2.9.1)。樹脂が流れている間は、ボールはレンズ側に寄っていますが(a)、型に樹脂が充填され、圧力の関係が逆転すると、今度はボールが注入側に押し戻され、封止されるわけです(b)。
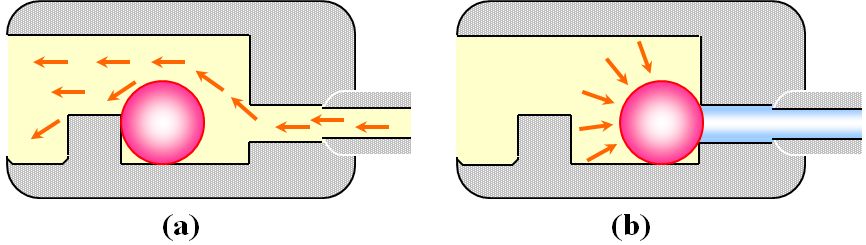 図2.9.1 ゲートシール法 |
|||||||||||||||||||||||||||||
 |
ラムネの原理と同じですね。
 図2.9.2 ラムネ(飲み口は炭酸の内部圧力によりビー玉で封止される) |
|||||||||||||||||||||||||||||
 |
はい。気づいてみれば単純なことなんですが、画期的なアイデアですね。図2.9.3のレンズが、ゲートシール法で成型されたものです。
 図2.9.3 ゲートシール法で成型されたレンズ(ゲート側に金属のボールが見える) |
|||||||||||||||||||||||||||||
 |
本当ですね。拡大すると、よく分かりますね。
 図2.9.4 ゲート部分の拡大写真 |
|||||||||||||||||||||||||||||
 | この発明により型内部の圧力を維持しながら時間をかけて樹脂を冷却することが可能となり、複屈折を抑えた成型ができるようになったのです。 | |||||||||||||||||||||||||||||
 | 現在の主流はシクロオレフィン樹脂ですか?? | |||||||||||||||||||||||||||||
 | そうですね。LSUに実装されている樹脂レンズのほぼ100%がシクロオレフィン樹脂を使っていると思います。 | |||||||||||||||||||||||||||||
 | 教授。PMMAはシクロオレフィン樹脂と同じくらい光弾性係数が小さいですけど?? | |||||||||||||||||||||||||||||
 | PMMAはキロ単価も安い材料なので広く使いたいところですが、屈折率が小さいのと、飽和吸水率が大きいのが欠点です。 | |||||||||||||||||||||||||||||
 | 飽和吸水率とは?? | |||||||||||||||||||||||||||||
 | 大気中の水分の吸収のしやすさですね。 | |||||||||||||||||||||||||||||
 | どうして困るんですか?? | |||||||||||||||||||||||||||||
 | 水分を吸収すると密度が高くなるため、屈折率が変化するからですよ。 |
~Lorentz-Lorenzの式~
 | 密度と屈折率って、何か関係性があるんですね?? | |
 |
あります。それをLorentz-Lorenzの式と言います。
 Ludvig Valentin Lorenz(1829~1891) |
|
 | ん??Lorentz-Lorenz??Duran Duranみたいなやつ?? | |
 | まったく違います。Duran Duranはグループの名前ですが、Lorentz-Lorenzは2人の物理学者の名前ですよ。同じ時期に独立に論文(論文)を発表したので、そのように呼ばれるのです。 | |
 | 偶然とは言え、同じ名前の人が同じ理論を考えるなんて、びっくりですね。 | |
 | この式は、誘電体外部から電場\(E\)を与えたとき、局所的な原子に対して、どのような電場が掛かっているか、というアプローチから導くことができます。 | |
 | どのような電場??外部電場\(E\)じゃないんですか?? | |
 | 注目している原子の周りで誘電分極が起こっているので、その寄与も考慮しないといけないですよね?? | |
 | あ、そうか。 | |
 | 注目している局所的な電場をLorentz電場と言いますが、これを\(\vec{\mathstrut E}_{\rm loc}\)と書きましょう。また、近くにある分極した原子からの寄与を\(\vec{\mathstrut E}_{\rm cont}\)とすれば、 \[ \vec{\mathstrut E}_{\rm loc} = \vec{\mathstrut E} + \vec{\mathstrut E}_{\rm cont} \tag{2.9.2} \] です。 | |
 | \(\vec{\mathstrut E}_{\rm cont}\)の形が分からないですね。 | |
 |
そこで、注目している原子を中心とする半径\(a\)の球を誘電体からくり抜くことを考えます。
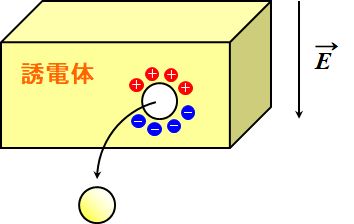 図2.9.5 誘電体に作られた球孔 すると、できた孔の表面に分極電荷が発生しますが、\(\vec{\mathstrut E}_{\rm cont}\)を「分極電荷によって生じる孔の中心位置の電場」というふうに読み替えてやるのです。 | |
 | 分極電荷の影響をすべて足し合わせないといけないのかぁ。 | |
 |
そこで、誘電分極\(\vec{\mathstrut P}\)と同じ向きに\(z\)軸を設定し、\(\theta\)を\(z\)軸から測った角度と定義します。このとき、分極電荷の面密度は\(P\cos\theta\)と表すことができます。
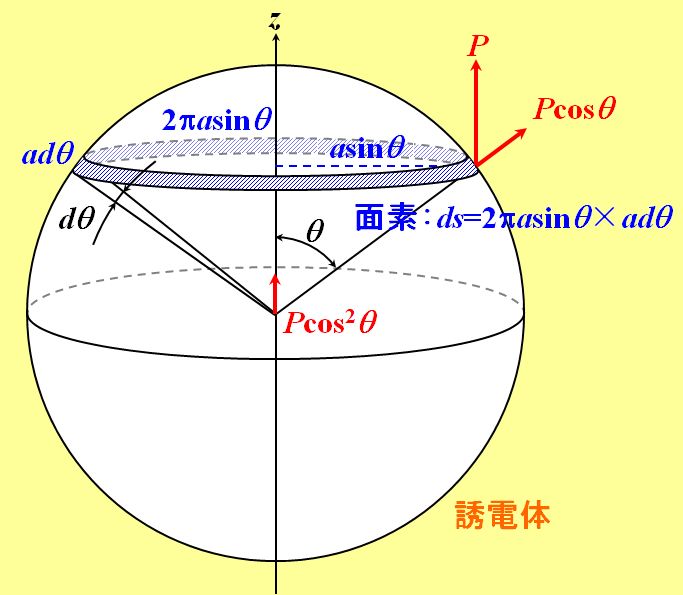 図2.9.6 \(\vec{\mathstrut E}_{\rm cont}\)の解法 |
|
 | これ、任意の\(z\)の位置にある帯で足し合わせると、\(xy\)平面では対称性が成立するから、\(z\)成分しか残らないですよね?? | |
 | そのとおりです。よって、ある\(z\)における分極電荷の寄与\(dE_{\rm cont}\)は、その位置での細い帯の面積を\(ds\)としたとき、Coulombの法則から、 \[ dE_{\rm cont} = \frac{1}{4 \pi \varepsilon_0} \frac{P \cos^2 \theta}{a^2} ds \tag{2.9.3} \] と書けます。 | |
 | 教授。Coulombの法則って、2つの電荷粒子に働く力の関係を示したものでは?? | |
 | そうですね。しかし、電場の定義は「単位電荷を置いたときに、その電荷が受ける静電気力」ですから、それを数式化すると、 \[ F = q_2 E \] です(\(q_2\)は荷電粒子の電荷)。Coulombの法則、 \[ F = k \frac{ q_1 q_2 }{ r^2 } \] と見比べれば、 \[ E = k \frac{ q_1 }{ r^2 } \] であるのは明らかであり、この式もCoulombの法則と呼ぶことがあります。 | |
 | \(k\)は比例定数だったけど、具体的には\(\cfrac{1}{4 \pi \varepsilon_0}\)ってことですね。 | |
 | 真空中の場合、という条件がありますけど。 | |
 | で、このケースだと、\(q_1\)は分極電荷の面密度ってことか。 | |
 | 正確には、さっき指摘していた「\(z\)成分しか残らない」ことを考慮し、 \[ dE_{\rm cont} = k \frac{P \cos \theta ds}{a^2} \times \cos \theta = k \frac{P \cos^2 \theta}{a^2} ds \] と計算したわけです。 | |
 | なるほど。 | |
 | では、\(ds\)はどう書けますか?? | |
 | 帯の円周が\(2\pi a\sin\theta\)で、帯の幅が\(ad\theta\)だから、 \[ ds = 2 \pi a \sin \theta \times a d \theta = 2 \pi a^2 \sin \theta d \theta \] かな?? | |
 | そうですね。\(E_{\rm cont}\)は式2.9.3を\(\theta\colon 0\sim\pi\)で積分すればOKです。 | |
 | ん~と。 \[ E_{\rm cont} = \int_0^{\pi} dE_{\rm cont} = \frac{1}{4 \pi \varepsilon_0} \int_0^{\pi} \frac{P \cos^2 \theta}{a^2} ds = \frac{1}{4 \pi \varepsilon_0} \int_0^{\pi} \frac{P \cos^2 \theta}{a^2} 2 \pi a^2 \sin \theta d \theta \] \[ = \frac{P}{2 \varepsilon_0} \int_0^{\pi} \cos^2 \theta \sin \theta d \theta = \frac{P}{2 \varepsilon_0} \left[ - \frac{1}{3} \cos^3 \theta \right]_0^{\pi} = \frac{P}{3 \varepsilon_0} \tag{2.9.4} \] | |
 | 式2.9.4を式2.9.2に代入すると、Lorentz電場が求まります。 \[ \vec{\mathstrut E_{\rm loc}} = \vec{\mathstrut E} + \frac{\vec{\mathstrut P}}{3 \varepsilon_0} \tag{2.9.5} \] | |
 | 結果だけ見ると、球の半径\(a\)は関係なくなっちゃうんですね。 | |
 | さて、局所的な電場が分かったので、局所的な電気双極子モーメント\(\vec{\mathstrut P_{\rm loc}}\)は、比例定数を\(\alpha\)と置いて、 \[ \vec{\mathstrut P_{\rm loc}} = \alpha \vec{\mathstrut E_{\rm loc}} \tag{2.9.6} \] と計算できます。この\(\alpha\)は分極率と言います。そして、\(\vec{\mathstrut P_{\rm loc}}\)が\(N\)個集まったものが誘電分極\(\vec{\mathstrut P}\)ですから、 \[ \vec{\mathstrut P} = N \vec{\mathstrut P_{\rm loc}} = N \alpha \vec{\mathstrut E_{\rm loc}} \tag{2.9.7} \] となるわけです。 | |
 | \(N\)は、前にやった「単位体積あたりの誘電分極に寄与する電子の数」ですね。式2.9.7に式2.9.5を代入すると、 \[ \vec{\mathstrut P} = N \alpha \left(\vec{\mathstrut E} + \frac{\vec{\mathstrut P}}{3 \varepsilon_0}\right) \quad \Leftrightarrow \quad \vec{\mathstrut P} \left( 1 - \frac{N \alpha}{3 \varepsilon_0} \right) = N \alpha \vec{\mathstrut E} \tag{2.9.8} \] となりますね。 | |
 | ここで、式1.9.5を思い出して、 \[ \vec{\mathstrut P} = \varepsilon_0 \left( \varepsilon_r - 1 \right) \vec{\mathstrut E} \tag{1.9.5} \] 式2.9.8を式1.9.5で割ります。 | |
 | ん~。教授。式1.9.5の議論では、外部電場は電磁波だから振動しているけど、式2.9.8を出すまでのここでの議論って、外部電場は静的なのでは?? | |
 | なかなか鋭い質問ですね。そのとおりです。静電場の議論が振動電場でも同じように成立するかどうかは自明ではありません。ですから、この議論は近似的に成立するという割り切りが必要です。 | |
 | ふ~ん。そうすると、 \[ 1 - \frac{N \alpha}{3 \varepsilon_0} = \frac{N \alpha}{\varepsilon_0 \left( \varepsilon_r - 1 \right)} \quad \Leftrightarrow \quad 1 = \frac{N \alpha}{3 \varepsilon_0} \left( 1 + \frac{3}{ \varepsilon_r - 1 } \right) = \frac{N \alpha}{3 \varepsilon_0} \frac{\varepsilon_r + 2}{\varepsilon_r - 1} \] \[ \Leftrightarrow \quad \frac{\varepsilon_r - 1}{\varepsilon_r + 2} = \frac{N \alpha}{3 \varepsilon_0} \tag{2.9.9} \] | |
 |
この式をClaudius-Mossottiの式と言います。
 Rudolf Julius Emmanuel Clausius(1822~1888) これに式1.8.5を代入したものが、Lorentz-Lorenzの式ですね。 \[ \frac{n^2 - 1}{n^2 + 2} \approx \frac{N \alpha}{3 \varepsilon_0} \tag{2.9.10} \] |
|
 | 教授。式2.9.10には、パラメータに密度ってないですけど?? | |
 | そこで、分子量を\(M\)、密度を\(d\)、Avogadro定数を\(N_A\)とすると、 \[ N = N_A \frac{d}{M} \tag{2.9.11} \] ですから、これを式2.9.10に代入すれば、 \[ \frac{n^2 - 1}{n^2 + 2} = \frac{N_A \alpha}{3 \varepsilon_0}\frac{d}{M} \tag{2.9.12} \] 密度との関係が導かれるわけです。 | |
 | なるほど。 | |
 | ちなみに、ここまでの議論では、媒質を構成している原子は1種類と仮定してましたが、複数ある場合は、\(i\)番目の原子の分極率を\(\alpha_i\)として、 \[ \frac{n^2 - 1}{n^2 + 2} = \sum_{i} \frac{N_A \alpha_i}{3 \varepsilon_0}\frac{d}{M} \tag{2.9.13} \] とすればOKです。 |
~樹脂の屈折率の求め方~
 | 式2.9.13を出発点にして、樹脂の屈折率を理論的に概算することができます。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | う~ん。\(\alpha\)が分かれば、確かに求まりそうだけど…。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | もう少し分かりやすいパラメータで置き換えてみましょう。 \[ \left[ R_i \right] \equiv \frac{N_A \alpha_i}{3 \varepsilon_0} \tag{2.9.14} \] \[ V_{\rm mol} \equiv = \frac{M}{d} \tag{2.9.15} \] ここで、\(\left[R_i\right]\)を原子屈折、\(V_{\rm mol}\)を分子容と言います。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 式2.9.13が、 \[ \frac{n^2 - 1}{n^2 + 2} = \sum_{i} \frac{\left[ R_i \right]}{V_{\rm mol}} \tag{2.9.16} \] に変わっただけで、分かりやすくなったようには思えないですけど?? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
原子屈折はデータがリスト化(下表はd線の結果)されてますし、分子容は組成式と密度が分かれば求まりますよね??
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 何か具体例を出してくださいよ~。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | その前に、式2.9.16を\(n\)の等式に直しましょう。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | それは…。 \[ n^2 - 1 = \left( n^2 + 2 \right) \sum \frac{\left[ R_i \right]}{V_{\rm mol}} \quad \Leftrightarrow \quad n^2 \left( 1 - \sum \frac{\left[ R_i \right]}{V_{\rm mol}} \right) = 1 + 2 \sum \frac{\left[ R_i \right]}{V_{\rm mol}} \] \[ \Leftrightarrow \quad n^2 = \frac{1 + 2 {\displaystyle \sum \cfrac{\left[ R_i \right]}{V_{\rm mol}}}}{1 - {\displaystyle \sum \cfrac{\left[ R_i \right]}{V_{\rm mol}}}} \quad \Leftrightarrow \quad n = \sqrt{ \frac{1 + 2 {\displaystyle \sum \cfrac{\left[ R_i \right]}{V_{\rm mol}}}}{1 - {\displaystyle \sum \cfrac{\left[ R_i \right]}{V_{\rm mol}}}} } \tag{2.9.17} \] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
では、PCを題材に屈折率を求めてみましょうか。
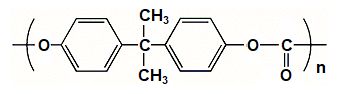 図2.9.7 PC(ポリカーボネート) まず、分子量\(M\)を求めます。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
炭素(C)が16個、酸素(O)が3個、水素(H)が14個だから、 \(M\) = 16 × 12.01 + 3 × 16 + 14 × 1.008 = 254.272 g/mol ですね。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 密度はカタログなどを見ればいいので、\(d\)=1.20g/cm3です。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
そうすると、分子容\(V_{\rm mol}\)は、 \(V_{\rm mol}\) = 254.272 g/mol ÷ 1.20 g/cm3 = 211.89 cm3/mol かな。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
で、原子屈折の用い方ですが、図2.9.7の構造式を図2.9.8のように分解するのです。
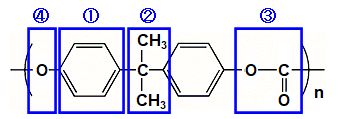 図2.9.8 PC(ポリカーボネート)の分子屈折 例えば、ベンゼン環(①)に注目すると、Cが6個、Hが4個、Cの2重結合が3個、6C環が1個と読めるので、この部分の分子屈折は、 \([R\)①\(]\) = 6 × 2.591 + 4 × 1.028 + 3 × 1.575 - 0.15 = 24.233 となります。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
じゃぁ、②の部分は、Cが3個、Hが6個で、 \([R\)②\(]\) = 3 × 2.591 + 6 × 1.028 = 13.941 ですか?? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | そうですね。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ③の部分はCOO(エステル基)で6.200、④の部分はO(エーテル基)で1.764ですね?? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
はい。というわけで、PCの分子屈折は、 \(\left[R\right]\) = 24.233 × 2 + 13.941 + 6.200 + 1.764 = 70.371 となり、屈折率は式2.9.17を使って、 \(n^2\) = ( 1 + 2 × 70.371 / 211.89 ) ÷ ( 1 - 70.371 / 211.89 ) = 2.4918 ∴\(n=1.58\) です。ほら、上の表と同じような数値(1.584)になってますよね?? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 本当だ~。PMMAも求まります?? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
PMMAの構造式は図2.9.9のようになっています。
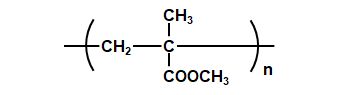 図2.9.9 PMMA(アクリル) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
そうすると、分子量\(M\)は、炭素(C)が5個、酸素(O)が2個、水素(H)が8個だから、 \(M\) = 5 × 12.01 + 2 × 16 + 8 × 1.008 = 100.114 g/mol |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 密度\(d\)は1.19g/cm3ですね。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
そうすると、分子容\(V_{\rm mol}\)は、 \(V_{\rm mol}\) = 100.114 g/mol ÷ 1.19 g/cm3 = 84.13 cm3/mol それで、構造式を分解して―。 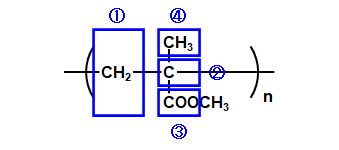 図2.9.10 PMMA(アクリル)の分子屈折 \([R\)①\(]\)はCH2(メチレン基)で4.647、\([R\)②\(]\)は2.591、\([R\)③\(]\)はCOO(エステル基)で6.200、\([R\)④\(]\)は2.591+3×1.028=5.675だから、PMMAの分子屈折は、 \(\left[R\right]\) = 4.647 + 2.591 + 6.200 + 2 × 5.675 = 24.788 よって、 \(n^2\) = ( 1 + 2 × 24.788 / 84.13 ) ÷ ( 1 - 24.788 / 84.13 ) = 2.2531 ∴\(n=1.50\) そこそこ合っている感じかな…(\(1.492\))。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | あくまで概算ですから、ピタッと一致することはないですよ。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | シクロオレフィン樹脂はどうかな?? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
シクロオレフィン樹脂はいろいろな種類がありますが、代表的なのは図2.9.11ですね(ZEONEX)。
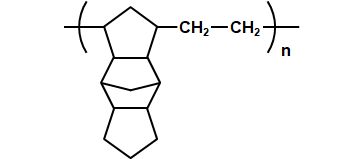 図2.9.11 CO(シクロオレフィン樹脂) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
そうすると、分子量\(M\)は、炭素(C)が15個、水素(H)22個だから、 \(M\) = 15 × 12.01 + 22 × 1.008 = 202.326 g/mol |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 密度\(d\)は1.01g/cm3ですね。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
そうすると、分子容\(V_{\rm mol}\)は、 \(V_{\rm mol}\) = 202.326 g/mol ÷ 1.01 g/cm3 = 200.32 cm3/mol それで、構造式を分解して―。 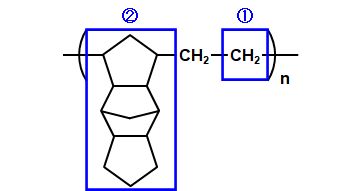 図2.9.12 CO(シクロオレフィン樹脂)の分子屈折 \([R\)①\(]\)はCH2(メチレン基)で4.647。\([R\)②\(]\)はCが13個、Hが18個、5C環が2個、6C環が1個だから、 \([R\)②\(]\) = 13 × 2.591 + 18 × 1.028 - 2 × 0.19 - 0.15 = 51.657 となって、シクロオレフィン樹脂の分子屈折は、 \(\left[R\right]\) = 2 × 4.647 + 51.657 = 60.951 よって、 \(n^2\) = ( 1 + 2 × 60.951 / 200.32 ) ÷ ( 1 - 60.951 / 200.32 ) = 2.3120 ∴\(n=1.52\) いい線、行ってますね(\(1.531\))。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | レンズ設計を考慮すると、プラスチックも高屈折率であることが望まれるわけですが、式2.9.17から、プラスチックの屈折率を大きくしたければ、分子屈折を高め、分子容を小さくすればいいことが分かります。しかし、たいていの樹脂の分子容は似たり寄ったりなので、原子屈折の高いものを組み合わせて分子屈折を高くするしかありません。そのための指針としては、①ベンゼン環を使う、②フッ素を除くハロゲン原子を使う、③硫黄原子を使う、などがありますね。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | PCの屈折率が比較的大きいのは、構造式の中にベンゼン環があるからなんですね。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ところが、ベンゼン環を持つポリマーは、1分子あたりの環の分極率が平面方向で123.1×10-25cm3、垂直方向で63.5×10-25cm3と差が大きいのが問題です。複屈折の起こりやすさは主分極率の差に比例するため、一般にベンゼン環を化学構造内に有するポリマーは複屈折を起こしやすいという欠点を持っています。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | PCの光弾性係数が大きいのは、そのせいなのか…。ベンゼン環は高屈折率を作れても副作用が大きいわけですね。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ハロゲン原子を使うと、射出成型時に脱ハロゲン化水素反応が起こりやすく、ポリマーの着色劣化による透過率の低下や、成型機のスクリューやシリンダの腐食といった悪影響を及ぼす欠点がありますね。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | そうすると、③しか残らないですけど?? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 硫黄原子を含むポリマーは、たいてい熱硬化性樹脂ですよ。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 射出成型では難しい、と…。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | というわけで、なかなか望みどおりの樹脂は手に入りにくいのが現状ですね。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 前にやったメタマテリアルが実用化したら、屈折率が自由に制御できるのでは?? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 可能性はありますね。そうなると、新しいレンズ設計の概念も誕生するかもしれません。 |
| 前頁へ | 戻る | 次頁へ |