 | 前回、4つのFresnel係数を導出しました。 | |
 | これですね。 \[ r_p \equiv \frac{ {a_p}^{\left( r \right)} }{ {a_p}^{\left( i \right)} } = \frac{ \tan \left( \theta_1 - \theta_2 \right) }{ \tan \left( \theta_1 + \theta_2 \right) } \tag{2.2.29} \] \[ t_p \equiv \frac{ {a_s}^{\left( t \right)} }{ {a_s}^{\left( i \right)} } = \frac{ 2 \sin \theta_2 \cos \theta_1 }{ \sin \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 - \theta_2 \right) } \tag{2.2.31} \] \[ r_s \equiv \frac{ {a_s}^{\left( r \right)} }{ {a_s}^{\left( i \right)} } = -\frac{ \sin \left( \theta_1 - \theta_2 \right) }{ \sin \left( \theta_1 + \theta_2 \right) } \tag{2.2.33} \] \[ t_s \equiv \frac{ {a_s}^{\left( t \right)} }{ {a_s}^{\left( i \right)} } = \frac{ 2 \sin \theta_2 \cos \theta_1 }{ \sin \left( \theta_1 + \theta_2 \right) } \tag{2.2.35} \] | |
 |
例えば、\(n_1=1\)、\(n_2=1.5\)とすると、それぞれは図2.3.1のようになります。
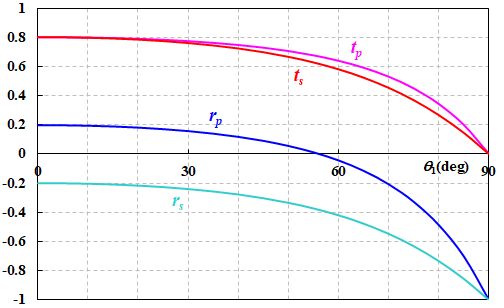 図2.3.1 Fresnel係数(振幅)の入射角依存性 |
|
 | \(r_p\)だけ\(0\)になる入射角があるんですね。 | |
 |
その角度\(\theta_{\rm B}\)を発見者(論文)の名前をとってBrewster角と言います。
 Sir David Brewster(1781~1868) Brewsterは1816年に万華鏡を発明して、それをカレイドスコープと命名し、3ヶ月で30万個売って結構なお金持ちになったことでも有名です。 |
|
 | 私も、そういう発明がしたいです!! | |
 | Brewster角の条件は\(r_p=0\)ですから、式2.2.29を使って、 \[ r_p = \frac{ \tan \left( \theta_1 - \theta_2 \right) }{ \tan \left( \theta_1 + \theta_2 \right) } = 0 \quad \Leftrightarrow \quad \tan \left( \theta_1 + \theta_2 \right) = \infty \quad \Leftrightarrow \quad \theta_1 + \theta_2 = \frac{ \pi }{ 2 } \] なので、これを式2.2.25に代入すると、 \[ r_p = \frac{ n_2 \cos \theta_1 - n_1 \cos \theta_2 }{ n_2 \cos \theta_1 + n_1 \cos \theta_2 } = 0 \\ \Leftrightarrow \quad n_2 \cos \theta_1 = n_1 \cos \theta_2 = n_1 \cos \left( \frac{ \pi }{ 2 } - \theta_1 \right) = n_1 \sin \theta_1 \\ \Leftrightarrow \quad \frac{ n_2 }{ n_1 } = \frac{ \sin \theta_1 }{ \cos \theta_1 } = \tan \theta_1 \] つまり、 \[ \theta_{\rm B } = \tan^{-1} \left( \frac{ n_2 }{ n_1 } \right) \tag{2.3.1} \] となります。 |
~カワセミはBrewster角を知っているか??~
 |
下の動画はカワセミが水面下の魚を捕まえる瞬間を捉えたものです。
|
|
 | 上手に魚をgetしますよね~。 | |
 | これを見て、不思議に思いませんか?? | |
 | う~ん。どうだろ?? | |
 | 我々は、水面に反射する太陽の光で水面下の様子は分かりませんよね。では、どうやってカワセミは水面下の情報を得ているのでしょう?? | |
 | お、そういうことか。 | |
 |
それについて考えてみましょう。太陽光はいろいろな偏光方向の光の寄せ集めですから、無偏光と呼ばれます。それが水面に反射したとしましょう。もし、カワセミがBrewster角を満たす角度で水面を観察したとすると、反射光はすべて\(s\)偏光となっていることになります。
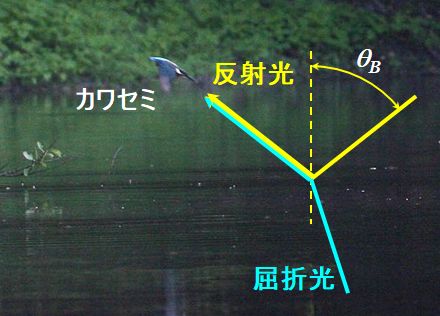 図2.3.2 カワセミはBrewster角を知っているか?? |
|
 | 水の屈折率は\(1.333\)くらいだから、\(\theta_{\rm B}=\tan^{-1}\left(1.333\right)=53.12^{\circ}\)ってところかな。 | |
 | ここで、カワセミの目は\(s\)偏光の光をカットするフィルターを持っている、とすると、カワセミには反射光が殆ど見えなくなります。つまり、ギラギラが消えわけです。 | |
 | でも、水面下から届く\(s\)偏光の光もカットされてしまいますよ?? | |
 | しかし、\(p\)偏光の成分は残ってますよね?? | |
 | そっか。だから、水面下の情報だけがくっきり見えるわけですね。 | |
 | こういうカラクリで、狙いの魚がどこを泳いでいるか一発で感知できるのです。写真撮影するときに、同様の機能を持つ偏光フィルターを使うことがよくありますね。 | |
 | 偏光フィルターが手に入れば、私たちも水面のギラギラが見えなくなる?? | |
 |
はい。これは、カメラの前に偏光フィルターをセットして水面を撮影し、偏光フィルターを回転させると、水面下がくっきり見えるデモンストレーション映像です。
|
|
 | お~。池の鯉がバッチリ見えますね!! | |
 | 自然界では、Brewster角が意外と重要な役割をしていることが分かります。 |
~強度換算のFresnel係数~
 | さて、Fresnel係数ですが、振幅での結果はあまり嬉しくありません。 | |
 | なぜですか?? | |
 | 測定できないからです。そこで、強度に変換したFresnel係数を求めておきましょう。 | |
 | 式2.2.29、式2.2.31、式2.2.33、式2.2.35を2乗すればいいのでは?? | |
 |
そう単純な話ではありません。まず、この議論では電磁波のエネルギーを考える必要があります。単位時間、単位面積あたりの電磁波のエネルギーは、
\[
\vec{\mathstrut S}=\vec{\mathstrut E} \times \vec{\mathstrut H} \tag{2.3.2}
\]
という計算で与えられます(論文)。これをPoyntingベクトルと言います。
 John Henry Poynting(1852~1914) |
|
 | Poyntingって、人の名前なの?? | |
 | そうですよ。それと、検知されるエネルギーは\(\vec{\mathstrut S}\)の時間平均であることを考慮しないといけません(\(T_0\)は観測時間)。 \[ \begin{align*} I &= \frac{ 1 }{ T_0 } \int_{0}^{T_0} \big| \vec{\mathstrut S} \big| dt = \frac{ \Big| \vec{\mathstrut E^{ \left(0\right)}} \Big| \Big| \vec{\mathstrut H^{ \left(0\right)}} \Big| }{ T_0 } \int_{0}^{T_0} \cos^2 \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi_0 \big) dt \\ &= \frac{ \Big| \vec{\mathstrut E^{ \left(0\right)}} \Big| \Big| \vec{\mathstrut H^{ \left(0\right)}} \Big| }{ T_0 } \int_{0}^{T_0} \frac{ \cos 2 \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi_0 \big) + 1 }{ 2 } dt \\ &= \frac{ \Big| \vec{\mathstrut E^{ \left(0\right)}} \Big| \Big| \vec{\mathstrut H^{ \left(0\right)}} \Big| }{ T_0 } \bigg[ \int_{0}^{T_0} \frac{ \cos 2 \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi_0 \big) }{ 2 } dt + \int_{0}^{T_0} \frac{ 1 }{ 2 } dt \bigg] \\ &= \frac{ \Big| \vec{\mathstrut E^{ \left(0\right)}} \Big| \Big| \vec{\mathstrut H^{ \left(0\right)}} \Big| }{ T_0 } \int_{0}^{T_0} \frac{ 1 }{ 2 } dt = \frac{ \Big| \vec{\mathstrut E^{ \left(0\right)}} \Big| \Big| \vec{\mathstrut H^{ \left(0\right)}} \Big| }{ T_0 } \left[ \frac{ t }{ 2 } \right]_0^{T_0} = \frac{ \Big| \vec{\mathstrut E^{ \left(0\right)}} \Big| \Big| \vec{\mathstrut H^{ \left(0\right)}} \Big| }{ 2 } \\ &= \frac { Y }{ 2 } \Big| \vec{\mathstrut E^{ \left(0\right)}} \Big|^2 \tag{2.3.3} \end{align*} \] | |
 | \(Y\)はアドミタンスですね。 | |
 | しかも、入射角\(\theta\neq0^{\circ}\)の場合は、\(\theta\)の分も考慮しないといけない。 | |
 | そうすると、\(p\)偏光のエネルギー反射率\(R_p\)は、 \[ R_p = \frac{ {I_p}^{\left(r\right)} }{ {I_p}^{\left(i\right)} } = \frac{ \cfrac{Y_1}{2} \{ {a_p}^{\left(r\right)} \}^2 \cos \theta_1 }{ \cfrac{Y_1}{2} \{ {a_p}^{\left(i\right)} \}^2 \cos \theta_1 } = \left( \frac{ {a_p}^{\left(r\right)} }{ {a_p}^{\left(i\right)} } \right)^2 = \frac{ \tan^2 \left( \theta_1 - \theta_2 \right) }{ \tan^2 \left( \theta_1 + \theta_2 \right) } \tag{2.3.4} \] \(s\)偏光のエネルギー反射率\(R_s\)は、 \[ R_s = \frac{ {I_s}^{\left(r\right)} }{ {I_s}^{\left(i\right)} } = \frac{ \cfrac{Y_1}{2} \{ {a_s}^{\left(r\right)} \}^2 \cos \theta_1 }{ \cfrac{Y_1}{2} \{ {a_s}^{\left(i\right)} \}^2 \cos \theta_1 } = \left( \frac{ {a_s}^{\left(r\right)} }{ {a_s}^{\left(i\right)} } \right)^2 = \frac{ \sin^2 \left( \theta_1 - \theta_2 \right) }{ \sin^2 \left( \theta_1 + \theta_2 \right) } \tag{2.3.5} \] ってこと?? | |
 | そうです。同じようにエネルギー透過率の方も求めてみてください。 | |
 | \(p\)偏光のエネルギー透過率\(T_p\)は、 \[ \begin{align*} T_p &= \frac{ {I_p}^{\left(t\right)} }{ {I_p}^{\left(i\right)} } = \frac{ \cfrac{Y_2}{2} \{ {a_p}^{\left(t\right)} \}^2 \cos \theta_2 }{ \cfrac{Y_1}{2} \{ {a_p}^{\left(i\right)} \}^2 \cos \theta_1 } = \left( \frac{ {a_p}^{\left(t\right)} }{ {a_p}^{\left(i\right)} } \right)^2 \frac{ \sqrt{\cfrac{\varepsilon_2}{\mu_2}} \cos \theta_2 }{ \sqrt{\cfrac{\varepsilon_1}{\mu_1}} \cos \theta_1 } \\ & \approx \left( \frac{ {a_p}^{\left(t\right)} }{ {a_p}^{\left(i\right)} } \right)^2 \frac{ \sqrt{\varepsilon_2} \cos \theta_2 }{ \sqrt{\varepsilon_1} \cos \theta_1 } \approx \left( \frac{ {a_p}^{\left(t\right)} }{ {a_p}^{\left(i\right)} } \right)^2 \frac{ n_2 \cos \theta_2 }{ n_1 \cos \theta_1 } = \left( \frac{ {a_p}^{\left(t\right)} }{ {a_p}^{\left(i\right)} } \right)^2 \frac{ \sin \theta_1 \cos \theta_2 }{ \sin \theta_2 \cos \theta_1 } \\ &= \frac{ 4 \sin^2 \theta_2 \cos^2 \theta_1 }{ \sin^2 \left( \theta_1 + \theta_2 \right) \cos^2 \left( \theta_1 - \theta_2 \right) } \frac{ \sin \theta_1 \cos \theta_2 }{ \sin \theta_2 \cos \theta_1 } = \frac{ 2 \sin \theta_1 \cos \theta_1 \times 2 \sin \theta_2 \cos \theta_2 }{ \sin^2 \left( \theta_1 + \theta_2 \right) \cos^2 \left( \theta_1 - \theta_2 \right) } \end{align*} \] \[ \phantom{T_p}= \frac{ \sin 2 \theta_1 \sin 2 \theta_2 }{ \sin^2 \left( \theta_1 + \theta_2 \right) \cos^2 \left( \theta_1 - \theta_2 \right) } \tag{2.3.6} \] \(s\)偏光のエネルギー透過率\(T_s\)は、 \[ \begin{align*} T_s &= \frac{ {I_s}^{\left(t\right)} }{ {I_s}^{\left(i\right)} } = \frac{ \cfrac{Y_2}{2} \{ {a_s}^{\left(t\right)} \}^2 \cos \theta_2 }{ \cfrac{Y_1}{2} \{ {a_s}^{\left(i\right)} \}^2 \cos \theta_1 } = \left( \frac{ {a_s}^{\left(t\right)} }{ {a_s}^{\left(i\right)} } \right)^2 \frac{ \sqrt{\cfrac{\varepsilon_2}{\mu_2}} \cos \theta_2 }{ \sqrt{\cfrac{\varepsilon_1}{\mu_1}} \cos \theta_1 } \\ & \approx \left( \frac{ {a_s}^{\left(t\right)} }{ {a_s}^{\left(i\right)} } \right)^2 \frac{ \sqrt{\varepsilon_2} \cos \theta_2 }{ \sqrt{\varepsilon_1} \cos \theta_1 } \approx \left( \frac{ {a_s}^{\left(t\right)} }{ {a_s}^{\left(i\right)} } \right)^2 \frac{ n_2 \cos \theta_2 }{ n_1 \cos \theta_1 } = \left( \frac{ {a_s}^{\left(t\right)} }{ {a_s}^{\left(i\right)} } \right)^2 \frac{ \sin \theta_1 \cos \theta_2 }{ \sin \theta_2 \cos \theta_1 } \\ &= \frac{ 4 \sin^2 \theta_2 \cos^2 \theta_1 }{ \sin^2 \left( \theta_1 + \theta_2 \right) } \frac{ \sin \theta_1 \cos \theta_2 }{ \sin \theta_2 \cos \theta_1 } = \frac{ 2 \sin \theta_1 \cos \theta_1 \times 2 \sin \theta_2 \cos \theta_2 }{ \sin^2 \left( \theta_1 + \theta_2 \right) } \end{align*} \] \[ \phantom{T_s}= \frac{ \sin 2 \theta_1 \sin 2 \theta_2 }{ \sin^2 \left( \theta_1 + \theta_2 \right) } \tag{2.3.7} \] | |
 | ついでに、式2.2.25、式2.2.32、式2.2.30、式2.2.34のアプローチからも計算しておきましょう。 | |
 | え~と。 \[ R_p = \left( \frac{ {a_p}^{\left(r\right)} }{ {a_p}^{\left(i\right)} } \right)^2 = \left( \frac{ n_2 \cos \theta_1 - n_1 \cos \theta_2 }{ n_2 \cos \theta_1 + n_1 \cos \theta_2 } \right)^2 \tag{2.3.8} \] \[ R_s = \left( \frac{ {a_s}^{\left(r\right)} }{ {a_s}^{\left(i\right)} } \right)^2 = \left( \frac{ n_1 \cos \theta_1 - n_2 \cos \theta_2 }{ n_1 \cos \theta_1 + n_2 \cos \theta_2 } \right)^2 \tag{2.3.9} \] \[ \begin{align*} T_p &= \left( \frac{ {a_p}^{\left(t\right)} }{ {a_p}^{\left(i\right)} } \right)^2 \frac{ n_2 \cos \theta_2 }{ n_1 \cos \theta_1 } = \frac{ 4 {n_1}^2 \cos^2 \theta_1 }{ \left( n_1 \cos \theta_2 + n_2 \cos \theta_1 \right)^2 } \frac{ n_2 \cos \theta_2 }{ n_1 \cos \theta_1 } \\ &= \frac{ 4 n_1 n_2 \cos \theta_1 \cos \theta_2 }{ \left( n_1 \cos \theta_2 + n_2 \cos \theta_1 \right)^2 } \tag{2.3.10} \end{align*} \] \[ \begin{align*} T_s &= \left( \frac{ {a_s}^{\left(t\right)} }{ {a_s}^{\left(i\right)} } \right)^2 \frac{ n_2 \cos \theta_2 }{ n_1 \cos \theta_1 } = \frac{ 4 {n_1}^2 \cos^2 \theta_1 }{ \left( n_1 \cos \theta_1 + n_2 \cos \theta_2 \right)^2 } \frac{ n_2 \cos \theta_2 }{ n_1 \cos \theta_1 } \\ &= \frac{ 4 n_1 n_2 \cos \theta_1 \cos \theta_2 }{ \left( n_1 \cos \theta_1 + n_2 \cos \theta_2 \right)^2 } \tag{2.3.11} \end{align*} \] | |
 | こちらの方が、エネルギー保存則を確認しやすいですね。例えば、\(p\)偏光だと、 \[ \begin{align*} R_p + T_p &= \left( \frac{ n_2 \cos \theta_1 - n_1 \cos \theta_2 }{ n_2 \cos \theta_1 + n_1 \cos \theta_2 } \right)^2 + \frac{ 4 n_1 n_2 \cos \theta_1 \cos \theta_2 }{ \left( n_1 \cos \theta_2 + n_2 \cos \theta_1 \right)^2 } \\ &= \frac{ {n_2}^2 \cos^2 \theta_1 - 2 n_1 n_2 \cos \theta_1 \cos \theta_2 + {n_1}^2 \cos^2 \theta_2 + 4 n_1 n_2 \cos \theta_1 \cos \theta_2 }{ \left( n_2 \cos \theta_1 + n_1 \cos \theta_2 \right)^2 } \\ &= \frac{ {n_2}^2 \cos^2 \theta_1 + 2 n_1 n_2 \cos \theta_1 \cos \theta_2 + {n_1}^2 \cos^2 \theta_2 }{ \left( n_2 \cos \theta_1 + n_1 \cos \theta_2 \right)^2 } \\ &= \frac{ \left( n_2 \cos \theta_1 + n_1 \cos \theta_2 \right)^2 }{ \left( n_2 \cos \theta_1 + n_1 \cos \theta_2 \right)^2 } = 1 \end{align*} \] | |
 | \(s\)偏光だと、 \[ \begin{align*} R_s + T_s &= \left( \frac{ n_1 \cos \theta_1 - n_2 \cos \theta_2 }{ n_1 \cos \theta_1 + n_2 \cos \theta_2 } \right)^2 + \frac{ 4 n_1 n_2 \cos \theta_1 \cos \theta_2 }{ \left( n_1 \cos \theta_1 + n_2 \cos \theta_2 \right)^2 } \\ &= \frac{ {n_1}^2 \cos^2 \theta_1 - 2 n_1 n_2 \cos \theta_1 \cos \theta_2 + {n_2}^2 \cos^2 \theta_2 + 4 n_1 n_2 \cos \theta_1 \cos \theta_2 }{ \left( n_1 \cos \theta_1 + n_2 \cos \theta_2 \right)^2 } \\ &= \frac{ {n_1}^2 \cos^2 \theta_1 + 2 n_1 n_2 \cos \theta_1 \cos \theta_2 + {n_2}^2 \cos^2 \theta_2 }{ \left( n_1 \cos \theta_1 + n_2 \cos \theta_2 \right)^2 } \\ &= \frac{ \left( n_1 \cos \theta_1 + n_2 \cos \theta_2 \right)^2 }{ \left( n_1 \cos \theta_1 + n_2 \cos \theta_2 \right)^2 } = 1 \end{align*} \] ですね。 | |
 | それと、垂直入射のときの反射率、透過率も計算できますね。 | |
 | それは、 \[ R_p = R_s = \frac{ \left( n_2 - n_1 \right)^2 }{ \left( n_2 + n_1 \right)^2 } \tag{2.3.12} \] \[ T_p = T_s = \frac{ 4 n_1 n_2 }{ \left( n_1 + n_2 \right)^2 } \tag{2.3.13} \] かな。 | |
 | 式2.3.12はよく使うので、覚えておくといいですよ。覚えやすい形してますしね。 |
~Lambert-Beerの法則~
 | 例えば、どういうときに使いますか?? | |
 |
これは㈱帝人のPCのスペック表です。
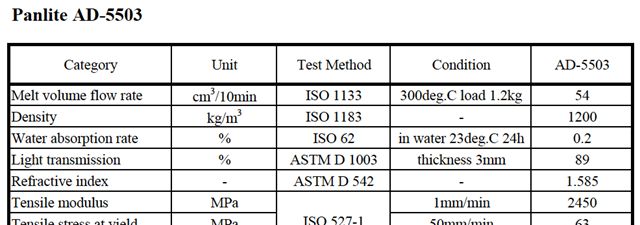 図2.3.3 PCのスペック表(㈱帝人) これを見て、肉厚が30mmのレンズをPCで作る場合、透過率はいくらになるか、というのを概算するときに使ったりします。 |
|
 | あれ??透過率が\(89\%\)??入射面の反射率\(R\)って、\(\cfrac{\left(1.585-1\right)^2}{\left(1.585+1\right)^2}=5.12\%\)だから、入射面の透過率\(T=94.88\%\)ですよね。2面あるから\(\left(94.88\%\right)^2=90.02\%\)になるのでは?? | |
 | つまり、その差額はレンズに吸収されているんですよ。 | |
 | ムムム。吸収を考慮しないといけない?? | |
 |
そうです。この場合の吸収率はLambertの法則に従う点に注意です。
 Johann Heinrich Lambert(1728~1777) |
|
 | どういう法則?? | |
 | 媒質に吸収される光エネルギーは、媒質の厚さが増加するに従って増加する、という法則です(論文)。 | |
 | それって、当たり前のような。だって、単位厚みあたりの吸収率を\(\alpha\)とすれば、そのときの透過エネルギーは\(\left(1-\alpha\right)\)ですよね。てことは、厚み\(d\)だったら、透過する光エネルギーは\(\left(1-\alpha\right)^d\)だけ低減するに決まってるじゃないですか。 | |
 | そう言えるのは、現代の感覚だからですよ。ただ、考え方は正しいです。 | |
 | モデル的には、媒質の原子とか分子が光を吸収するってことですよね?? | |
 | そうですね。厚みが増えると、それだけ光を吸収する原子や分子が増加するから、上記のような議論になっていきます。 | |
 | ということは、厚みを増やさなくても、単位厚みの媒質の中に存在する原子とか分子の数を増やしても、同じことでは?? | |
 |
なかなか鋭いですね。つまり、濃度によっても同じような法則が成立します。これをBeerの法則(論文)と言います。
 Pierre Bouguer(1698~1758) |
|
 | あら。すでに知られている?? | |
 | 1852年には。 | |
 | な~んだ。 | |
 | なので、併せてLambert-Beerの法則と呼ぶのが一般的ですね。さて、そうすると、この問題では、まず吸収率\(\alpha\)を求める必要があります。 | |
 | う~ん。入射面で透過率\(T=94.88\%\)だから、これが媒質を透過する過程で\(\left(1-\alpha\right)^3\)に低下して出射面に到達するのか。で、そこでまた透過率\(T=94.88\%\)が成立するから、\(89\%=94.88\%×\left(1-\alpha\right)^3\times94.88\%\)となりそうですね。 | |
 | つまり、\(\left(1-\alpha\right)^3=89\%\div\left(94.88\%\times94.88\%\right)=98.86\%\)です。求めたいのは、30mmの厚さだから…。 | |
 | \(\left(1-\alpha\right)^{30}=\left(98.86\%\right)^{10}=89.17\%\)。てことは、\(T=94.88\%\times89.17\%\times94.88\%=80.27\%\)が正解?? | |
 | はい。例えば、あるメーカーが新しいレンズの材料を開発したから検討してほしい、というような話はちょくちょくあるのです。そのときに、この式を知っていると、スペック表から、こういう計算をササッと電卓でやって、その場で使える材料か使えない材料かが判断できるんですよ。 | |
 | なるほど。 | |
 |
最後に、\(n_1=1\)、\(n_2=1.5\)の場合のFresnel係数の入射角依存性を確認しておきましょう。
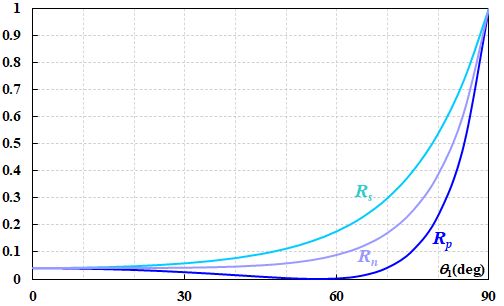 図2.3.4 Fresnel係数(エネルギー)の入射角依存性(反射率) 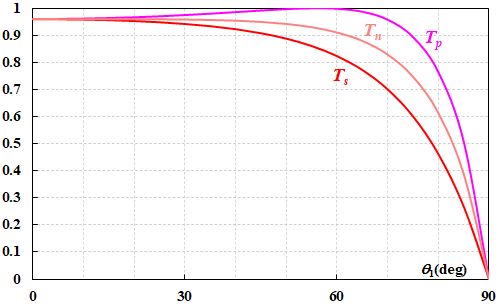 図2.3.5 Fresnel係数(エネルギー)の入射角依存性(透過率) |
|
 | \(R_n\)とか\(T_n\)がありますけど?? | |
 | それは自然光という意味です。つまり、無偏光のとき、或いは円偏光のときの結果になります。ちょうど\(p\)偏光と\(s\)偏光がevenに混ざっている状況と等価ですね。 | |
 | \(R_p=0\)になるところがBrewster角ですね。 | |
 | そうです。このグラフの形も覚えておくといいですよ。 |
| 前頁へ | 戻る | 次頁へ |