 |
前回までは\(n_1 < n_2 \)という条件で議論しましたが、今回は\(n_1=1.5\)、\(n_2=1\)のケースを考えましょう。
 図2.4.1 \(n_1>n_2\) このとき、エネルギー反射率は次のようなグラフになります。 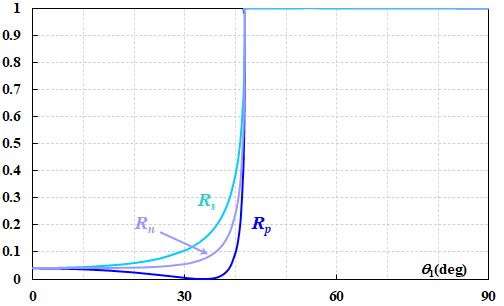 図2.4.2 エネルギー反射率の入射角依存性 |
|
 | あれ??途中から反射率が\(100\%\)にへばりついてますね。 | |
 | そのような現象は全反射と呼ばれ、その始まりの角度\(\theta_C\)を臨界角と言います。 | |
 | 今度は臨界角かぁ。 | |
 | 臨界角の条件は\(\theta_2=90^{\circ}\)ですから、式2.2.26より、 \[ n_1 \sin \theta_C = n_2 \quad \Leftrightarrow \quad \sin \theta_C = \frac{ n_2 }{ n_1 } \quad \Leftrightarrow \quad \theta_C = \sin^{-1} \frac{ n_2 }{ n_1 } \tag{2.4.1} \] となります。 |
〜エバネッセント波〜
 | 実は、全反射の領域では、なかなか興味深い現象が起こっています。 | |
 | 特異点だから、何かありそうですね。 | |
 | \(\theta_1>\theta_C\)の条件のとき、 \[ \begin{align*} \cos \theta_2 &= \pm \sqrt{ 1 - \sin^2 \theta_2 } = \pm \sqrt{ 1 - \left( \frac{ n_1 \sin \theta_1 }{ n_2 } \right)^2 } = \pm \sqrt{ \frac{ {n_2}^2 - {n_1}^2 \sin^2 \theta_1 }{ {n_2}^2 } } \\ &= \pm \sqrt{ -1 \times \left( \frac{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 }{ {n_2}^2 } \right) } = \pm i \frac{ \sqrt{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 }}{n_2 } \end{align*} \] ですね?? | |
 | 何か、強引に計算している感じがしますけど…。 | |
 | まぁ、そこは目を瞑ります。そうすると、屈折光の波数の単位ベクトルが、次のように書けます。 \[ {s_x}^{\left(t\right)} = \sin \theta_2 = \frac{ n_1 \sin \theta_1 }{ n_2 } \] \[ {s_z}^{\left(t\right)} = \cos \theta_2 = \pm i \frac{ \sqrt{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 }}{n_2 } \] | |
 | \({s_y}^{\left(t\right)}\)は入射平面内にあるから、\(0\)ってことですね。 | |
 | これらを、式2.2.2に代入すると、 \[ \begin{align*} \vec{\mathstrut E^{\left(t\right)}} &= a^{\left(t\right)} \exp \left[ i \omega \left( \frac{ {s_x}^{ \left(t\right)} x + {s_z}^{\left(t\right)} z }{ v_2 } - t \right) \right] \\ &= a^{\left(t\right)} \exp \left[ i \omega \frac{ {s_z}^{\left(t\right)} z }{ v_2 } \right] \exp \left[ i \omega \left( \frac{ {s_x}^{ \left(t\right)} x }{ v_2 } - t \right) \right] \\ &= a^{\left(t\right)} \exp \left[ \pm \omega \frac{ \sqrt{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 }}{ n_2 } \frac{ z }{ v_2 } \right] \exp \left[ i \omega \left( \frac{ n_1 \sin \theta_1 }{ n_2 } \frac{ x }{ v_2 } - t \right) \right] \\ &= a^{\left(t\right)} \exp \left[ \pm \omega \frac{ \sqrt{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 }}{ c } z \right] \exp \left[ i \omega \left( \frac{ n_1 \sin \theta_1 }{ c } x - t \right) \right] \tag{2.4.2} \end{align*} \] となります。 | |
 | 右辺の1つ目の指数関数は、プラスだと\(z\)の増加に伴って発散しちゃいますね。 | |
 | というわけで、式2.4.2で意味のあるのはマイナスのみだと分かります。 \[ \vec{\mathstrut E^{\left(t\right)}} = a^{\left(t\right)} \exp \left[ - \omega \frac{ \sqrt{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 }}{ c } z \right] \exp \left[ i \omega \left( \frac{ n_1 \sin \theta_1 }{ c } x - t \right) \right] \tag{2.4.3} \] | |
 | 教授。この式が意味していることって何ですか?? | |
 |
全反射という現象は、境界面を越えたエネルギーの流れが存在しないということであって、媒質2に電磁場が存在しないわけではない、ということです。
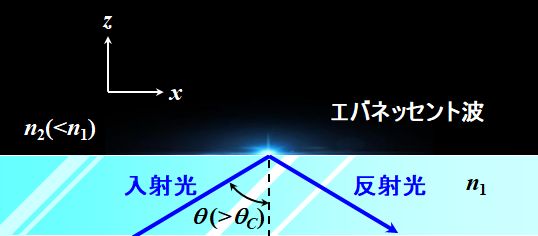 図2.4.3 エバネッセント波 |
|
 | ん??媒質2にジワッと染み出しているってこと?? | |
 | そうです。全反射が起こるまでは屈折光として媒質2を伝搬するパスがあったのに、臨界角でそのパスが突然なくなってしまうわけですから、光の立場からすると「アレ??」ってなりますよね。 | |
 | 車は急に止まれない、ってやつ?? | |
 | イメージ的には。 | |
 | ふ〜ん。そういう"おっとっと光"が存在するってことか。 | |
 | 名前がありますよ。エバネッセント波と言います。 | |
 | エバネッセント?? | |
 | 儚いとか、そういう意味ですね。 | |
 | 儚い光かぁ。ロマンチックですね〜。 | |
 | どのくらい儚いかというと、振幅の\(\cfrac{1}{\mathrm{e}}\)くらいが意味のある染み出し量なので、 \[ \frac{ \omega }{ c } \sqrt{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 } \cdot z_d = 1 \quad \Leftrightarrow \quad k \sqrt{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 } \cdot z_d = 1 \\ \Leftrightarrow \quad z_d = \frac{ 1 } { k \sqrt{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 } } = \frac{ \lambda } { 2 \pi \sqrt{ {n_1}^2 \sin^2 \theta_1 -{n_2}^2 } } \] 高々、波長くらいの深さしか染み出してません。 | |
 | \(n_1=1.5\)、\(n_2=1\)、\(\theta=45^{\circ}\)だと、\(z_d=0.45\lambda\)ですね。 | |
 | このエバネッセント波は媒質2を伝搬しないので、前にやった局在波だと考えられます。 | |
 | ということは、エバネッセント波を利用すると、微小な情報を得ることが可能ってことですね?? | |
 |
例えば、エバネッセント波に極細のプローブを当ててやると散乱しますので、その微弱散乱光を検知することでプローブの高さ方向の情報が得られます。その原理を利用すれば、プローブを走査させることで被検物の形状を取得することができるのです。
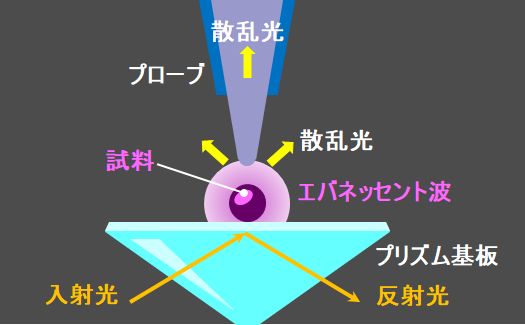 図2.4.4 SNOM こういう装置は、走査型近接場光顕微鏡(SNOM:scanning near field optical microscopy)と呼ばれます。 |
|
 | なるほど。 | |
 |
SNOMは被検物に殆どダメージを与えないというメリットがありますし、真空中や乾燥といった環境に弱い細胞などを観察するときにも利用できます。この顕微鏡はSyngeによって提案された(論文)のですが、実現性が乏しいということで一時期、忘れ去られていました。
 Edward Hutchinson Synge(1890〜1957) |
|
 | う〜ん。早すぎるアイデアって損ですね…。 | |
 |
しかし、1984年になってPohlの研究(論文)により実用化の目途が付くのです。
 Wolfgang Dieter Pohl(1938〜) |
|
 | 教授。式2.4.3を見ると、エバネッセント波って、\(x\)方向に伝搬してますよね?? | |
 | そうですね。エネルギーの流れは\(x\)方向にのみ存在します。 | |
 | ってことは、はみ出した光は、元の位置に戻って来ないってこと?? | |
 | そういうことになりますね。 | |
 | え〜。冗談で言ったのに〜。入射するポイントと反射するポイントは一致してないんですね?? | |
 |
この現象(論文)はGoos-Hänschensシフトと言います。可視光だと数μm程度ずれますよ。
 図2.4.5 Goos-Hänschensシフト |
|
 | うっ!!意外と大きい…。 | |
 | 全反射は、波動光学で考えると、面白い結果がいろいろ出てくるんですよ。 |
〜光ファイバー〜
 | 全反射という現象を上手く利用すると光を閉じ込めることができます。 | |
 | そっか。屈折率の高い媒質を、屈折率の低い媒質で包むと閉じ込められそうですね。 | |
 |
その最もポピュラーな具体例は光ファイバーでしょう。
 図2.4.6 光ファイバー 光ファイバーの屈折率の高い方(\(n_f\))をコア、低い方(\(n_c\))をクラッドと言います。 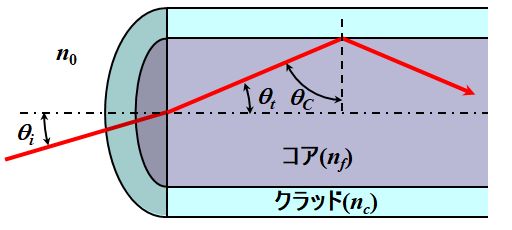 図2.4.7 光ファイバーの構造 |
|
 | コアに光を入射する角度が重要ですね。 | |
 | まず、コアとクラッドの境界面で全反射を起こす条件がありますね。 \[ n_f \sin \theta_C \geq n_c \tag{2.4.4} \] それと、コアに入射するときにSnellの法則が成立します。 \[ n_0 \sin \theta_i = n_f \sin \theta_t = n_f \sin \left( \frac{\pi}{2} - \theta_C \right) = n_f \cos \theta_C \tag{2.4.5} \] | |
 | そしたら、式2.4.4に式2.4.5を代入すればよさそうですね。 \[ \begin{align*} &n_f \sqrt{ 1 - \cos^2 \theta_C } \geq n_c \quad \Leftrightarrow \quad \sqrt{ 1 - \left( \frac{ n_0 }{ n_f } \sin \theta_i \right)^2 } \geq \frac { n_c }{ n_f } \\ &\Leftrightarrow \quad 1 - \left( \frac{ n_0 }{ n_f } \sin \theta_i \right)^2 \geq \left( \frac { n_c }{ n_f } \right)^2 \quad \Leftrightarrow \quad { n_0 }^2 \sin^2 \theta_i \leq {n_f}^2 - { n_c }^2 \\ &\Leftrightarrow \quad n_0 \sin \theta_i \leq \sqrt { {n_f}^2 - { n_c }^2 } \tag{2.4.6} \end{align*} \] | |
 |
図2.4.7のタイプはステップ・インデックス型と呼ばれている基本的なものですが、他にも用途に合わせていろいろなタイプが提案されてます。元々は、インド国籍の物理学者Kapanyによって発明されました(論文)が、最初は上手く伝送させることができませんでした。
 Narinder Singh Kapany(1926〜2020) |
|
 | なぜですか?? | |
 | コア部分のエネルギー損失が大きかったからです。尤も、Kapanyは内視鏡の画像伝送技術に光ファイバーを応用しようと考えていたので、長距離通信に発展させる発想はなかったと思いますし、他の研究者も理想状態における理論構築をメインにしていたので、エネルギー損失に着目する研究者がいませんでした。そこにメスを入れたのがKaoという物理学者です。 | |
 | この発想の切り替えが重要なんだよなぁ。 | |
 |
Kaoが研究するまで、エネルギー損失は反射部の散乱によるもので、物理学的には止むを得ないと考えられていたのですが、Kaoが主張したことは、その主要因はコア部分の不純物によるもので、損失率が1kmあたり20dB以下になれば通信に応用できるという画期的なもの(論文)だったのです。
 Sir Charles Kuen Kao(1933〜 2018) |
|
 | エネルギー損失が人工的に解決できる問題によるものだ、と分かれば、後の開発は一気に加速しますよね。 | |
 | 尤も、損失率だけで光ファイバーの課題がすべてクリアできるわけではありませんが、実用化を大きくドライブさせたのは間違いないでしょう。Kaoは、この功績により2009年にノーベル物理学賞をとってます。 | |
 | ということは、Kapanyとの共同受賞?? | |
 | いえ。光ファイバーとしては単独です。 | |
 | え〜、それは変じゃないですか?? | |
 |
理由は分からないですが、ノーベル賞に関しては、人種差別意識があるという批判は昔からあって、例えばBose粒子で有名なSatyendra Nath Boseや、
 Satyendra Nath Bose(1894〜1974) 量子光学で有名なSudarshanも超重要人物ですが、  Ennackal Chandy George Sudarshan(1931〜2018) ノーベル物理学賞は獲ってません。いずれもインド国籍です。 |
|
 | ふ〜ん。21世紀になっても、そういう問題は完全にはなくならないものなんですね。 | |
 | 政治的な事情もあったりしますしね。 | |
 | 光ファイバーの実用上の問題って、他には何がありますか?? | |
 | 温度による屈折率変動とか、ファイバーの曲げ損失とか、ですかね。今どきは工作キットとかで安く手に入りますが、測定器などで使用されるファイバーは高価なので、取り扱いは要注意です。折れたら修復がきかないので。 | |
 | う〜ん。あまり触らないようにしよっと。 | |
 | また、通信で使う場合は、大量の情報を伝送させるため、光ファイバーを束ねることがありますが、その際は伝送経路による遅延時間を気にしないといけないでしょう。 | |
 | 入射角によって伝送経路が違ってきそうですね。 | |
 | 一番早く伝送するのは\(\theta_i\)がいくつのときですか?? | |
 | \(\theta_i=0^{\circ}\)だと、そのまま中心をズドンと伝送するから最短経路だと思います。 | |
 | では、一番遅く伝送するのは、どういう条件を満たすときですか?? | |
 |
それは、臨界角\(\theta_C\)で伝送するときでは??
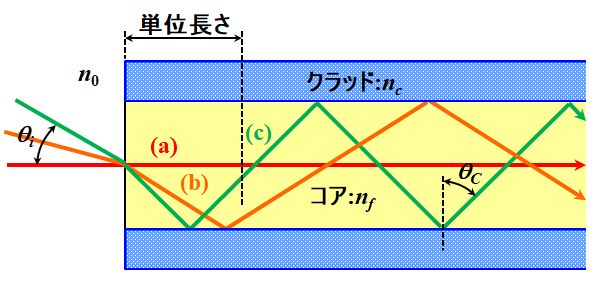 図2.4.8 遅延時間 |
|
 | とすると、最小経路(a)と最大経路(c)の単位長さあたりの遅延距離\(\Delta d\)は、 \[ \Delta d = \frac{ 1 }{ \sin \theta_C } - 1 = \frac{ n_f }{ n_c } - 1 \tag{2.4.7} \] となりますね?? | |
 | てことは、コアを伝送する光の速度を\(v_f\)とすると、遅延時間\(\Delta t\)は、 \[ \Delta t \leq \frac{ \Delta d }{ v_f } = \frac{ 1 }{ v_f } \left( \frac{ n_f }{ n_c } - 1 \right) = \frac{ n_f }{ c } \left( \frac{ n_f }{ n_c } - 1 \right) \tag{2.4.8} \] ですね。 | |
 | 例えば\(n_f=1.5\)、\(n_c=1.489\)とすると1kmで37nsの差異が発生しうることになります。 | |
 | 札幌から沖縄まで2,246kmだから、約80μsの遅延ですね。意外と大きいかも。 | |
 | これを改善するには、コアとクラッドの屈折率差を小さくしていけばいいのです。よく利用されるのは、屈折率差が0.2〜0.3%程度の組み合わせですね。 | |
 | 通信技術はどんどん高速化していくから、もっといろんな工夫が必要になってきそうですね。 |
| 前頁へ | 戻る | 次頁へ |