 | ん??前にやりませんでしたっけ?? | |
 | よく見てください。吸収媒質に変わってます。 | |
 | あ、本当だ!!ということは、誘電体ではない?? | |
 | 光を吸収するのは自由電子ですから、これは金属とか半導体が具体例となります。 | |
 | そうすると、\(\vec{\mathstrut j}\neq0\)だし、\(\rho\neq0\)ってこと?? | |
 | それはそうなんですが…。とりあえず、式1.3.1に式1.3.7、式1.3.8を代入した、 \[ \nabla \times \vec{\mathstrut H} = \vec{\mathstrut j} + \frac{ \partial \vec{\mathstrut D} }{ \partial t } = \frac{ \sigma }{ \varepsilon } \vec{\mathstrut D} + \frac{ \partial \vec{\mathstrut D} }{ \partial t } \tag{2.5.1} \] を考え、この両辺に\(\nabla\)・を演算してください。 | |
 | え〜と。 \[ \nabla \cdot \big( \nabla \times \vec{\mathstrut H} \big) = \frac{ \sigma }{ \varepsilon } \big( \nabla \cdot \vec{\mathstrut D} \big) + \frac{ \partial }{ \partial t } \big( \nabla \cdot \vec{\mathstrut D} \big) = \frac{ \sigma }{ \varepsilon } \rho + \frac{ \partial \rho }{ \partial t } \tag{2.5.2} \] 最後は、式1.3.3を代入しましたけど…。 | |
 | 左辺は公式により\(0\)です。 | |
 | お、そうすると―。 \[ \begin{align*} &\frac{ \partial \rho }{ \partial t } = - \frac{ \sigma }{ \varepsilon } \rho \quad \Leftrightarrow \quad \frac{ d \rho }{ \rho } = - \frac{ \sigma }{ \varepsilon } dt \quad \Leftrightarrow \quad \ln \frac{ \rho }{ \rho_0 } = - \frac{ \sigma }{ \varepsilon } t \\ &\Leftrightarrow \quad \frac{ \rho }{ \rho_0 } = \exp \left( - \frac{ \sigma }{ \varepsilon } t \right) \quad \Leftrightarrow \quad \rho = \rho_0 \exp \left( - \frac{ \sigma }{ \varepsilon } t \right) \tag{2.5.3} \end{align*} \] \(\rho_0\)は\(t=0\)のときの電荷密度としました。 | |
 | \(\cfrac{\varepsilon}{\sigma}\)は緩和時間と言いますが、例えば銅の緩和時間は2.7×19-14sです。従って、\(\rho\)は短い時間で急速に\(0\)になると考えてよく、無視して構いません。 | |
 | そうすると、 \[ \nabla \times \vec{\mathstrut H} = \vec{\mathstrut j} + \frac{ \partial \vec{\mathstrut D} }{ \partial t } \quad \Big( \Leftrightarrow \nabla \times \vec{\mathstrut H} = \sigma \vec{\mathstrut E} + \varepsilon \frac{ \partial \vec{\mathstrut E} }{ \partial t } \Big) \tag{2.5.4} \] \[ \nabla \times \vec{\mathstrut E} = - \frac{ \partial \vec{\mathstrut B} }{ \partial t } \quad \Big( \Leftrightarrow \nabla \times \vec{\mathstrut E} = - \mu \frac{ \partial \vec{\mathstrut H} }{ \partial t } \Big) \tag{2.5.5} \] \[ \nabla \cdot \vec{\mathstrut D} = 0 \quad \Big( \Leftrightarrow \nabla \cdot \vec{\mathstrut E} = 0 \Big) \tag{2.5.6} \] \[ \nabla \cdot \vec{\mathstrut B} = 0 \quad \Big( \Leftrightarrow \nabla \cdot \vec{\mathstrut H} = 0 \Big) \tag{2.5.7} \] ですね。 | |
 | では、まず式2.5.5に\(\nabla\times\)を演算してください。 | |
 | 前と同じかな…。まず、左辺から―。 \[ \nabla \times \big( \nabla \times \vec{\mathstrut E} \big) = - \nabla^2 \vec{\mathstrut E} \] ですね。で、右辺は、 \[ - \nabla \times \mu \frac{ \partial \vec{\mathstrut H} }{ \partial t } = - \mu \frac{ \partial }{ \partial t } \big( \nabla \times \vec{\mathstrut H} \big) = - \mu \frac{ \partial }{ \partial t } \Big( \sigma \vec{\mathstrut E} + \varepsilon \frac{ \partial \vec{\mathstrut E} }{ \partial t } \Big) = - \mu \sigma \frac{ \partial \vec{\mathstrut E} }{ \partial t } - \mu \varepsilon \frac{ \partial^2 \vec{\mathstrut E} }{ \partial t^2 } \] だから、 \[ \nabla^2 \vec{\mathstrut E} = \mu \sigma \frac{ \partial \vec{\mathstrut E} }{ \partial t } + \mu \varepsilon \frac{ \partial^2 \vec{\mathstrut E} }{ \partial t^2 } \tag{2.5.8} \] かな。 | |
 | そしたら、この解を式1.9.2のように置いてみましょう。\[ \vec{E} \big( \vec{\mathstrut r}, t \big) = E \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } \tag{1.9.2} \] | |
 | 式2.5.8に式1.9.2を代入すればいいのか…。 \[ \begin{align*} &\nabla^2 E \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } = -i \mu \sigma \omega E \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } - \mu \varepsilon \omega^2 E \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } \\ &\Leftrightarrow \quad \nabla^2 E \big( \vec{\mathstrut r} \big) = - \omega^2 \left( \varepsilon + i \frac{ \sigma }{ \omega } \right) \mu E \big( \vec{\mathstrut r} \big) \tag{2.5.9} \end{align*} \] | |
 | ここで、 \[ \tilde{\varepsilon} \equiv \varepsilon + i \frac{ \sigma }{ \omega } \tag{2.5.10} \] とし、これを複素誘電率と定義しましょう。また、式1.4.7に対応させて、 \[ \tilde{v} \equiv \frac{ 1 }{ \sqrt{ \tilde{\varepsilon} \mu } } \tag{2.5.11} \] を複素位相速度、式1.8.4に対応させて、 \[ \tilde{n} \equiv \frac{ c }{ \tilde{ v } } \tag{2.5.12} \] を複素屈折率、式1.11.6に対応させて、 \[ \tilde{k} \equiv \frac{ \omega }{ \tilde{ v } } = \frac{ \omega }{ c } \tilde{n} = \frac{ 2 \pi }{ c T } \tilde{n} = \frac { 2 \pi }{ \lambda } \tilde{n} \tag{2.5.13} \] を複素波数と定義します。 | |
 | 要するに、すべて複素数になったってことですね。 | |
 | 特に、複素屈折率は、 \[ \tilde{n} = n + i \kappa \tag{2.5.14} \] と書くことがあります。\(\kappa\)は消衰係数と呼びます。 | |
 | 消衰?? | |
 | 非吸収媒質にはなかった項が吸収媒質で出現したわけですから、意味としては光の吸収の程度を表していると考えればよいです。名前の由来は、次のように考えると理解できるでしょう。この媒質中を伝搬する電場は式1.1.13から、 \[ \begin{align*} \vec{\mathstrut E} \big( \vec{\mathstrut r},t \big) &= \vec{\mathstrut E^{\left(0\right)}} \exp \bigg[ i \Big( \tilde{k} \vec{\mathstrut s} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \Big) \bigg] = \vec{\mathstrut E^{\left(0\right)}} \exp \bigg[ i \Big( \frac { 2 \pi }{ \lambda } \tilde{n} \vec{\mathstrut s} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \Big) \bigg] \\ &= \vec{\mathstrut E^{\left(0\right)}} \exp \bigg[ i \Big( \frac { 2 \pi }{ \lambda } \big[ n + i \kappa \big] \vec{\mathstrut s} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \Big) \bigg] \end{align*} \] \[ \phantom{\vec{\mathstrut E} \big( \vec{\mathstrut r},t \big)}= \vec{\mathstrut E^{\left(0\right)}} \exp \bigg[ - \frac { 2 \pi }{ \lambda } \kappa \vec{\mathstrut s} \cdot \vec{\mathstrut r} \bigg] \exp \bigg[ i \Big( \frac { 2 \pi }{ \lambda } n \vec{\mathstrut s} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \Big) \bigg] \tag{2.5.15} \] と書けます。式2.5.15の右辺の2つ目の指数関数は通常の波動を意味しますが―。 | |
 | 1つ目の指数関数は波動が進行するにつれて減衰していきますね。だから、消衰係数なのか…。 | |
 | というわけで、金属や半導体の境界面における現象は殆ど反射によってのみ観測されるということになります。 |
〜Fresnelの反射係数〜
 | そうすると、Fresnel係数も反射率だけをケアすればいい?? | |
 | そうですね。基本的には式2.2.29と式2.2.33を使えばよいです。 \[ r_p = \frac{ \tan \left( \theta_1 - \theta_2 \right) }{ \tan \left( \theta_1 + \theta_2 \right) } \tag{2.2.29} \] \[ r_s = -\frac{ \sin \left( \theta_1 - \theta_2 \right) }{ \sin \left( \theta_1 + \theta_2 \right) } \tag{2.2.33} \] | |
 | でも、Snellの法則が、 \[ n_1 \sin \theta_1 = \tilde{n}_2 \sin \theta_2 \tag{2.5.16} \] になるから、\(\theta_2\)は複素数になりますよね。そうすると、Fresnel係数も複素数?? | |
 | 当然そうなりますね。そこで、それぞれの係数を、 \[ r_p = \rho_p \mathrm{e}^{i \psi_p} \tag{2.5.17} \] \[ r_s = \rho_s \mathrm{e}^{i \psi_s} \tag{2.5.18} \] と書きましょう。 | |
 | 指数関数がくっ付いてますけど?? | |
 | 誘電体の場合、屈折率の大きい媒質に入射した光の反射光は\(\pi\)の位相変化を受けましたね?? | |
 | はい。 | |
 | とすると、ここで扱っている媒質の反射光も位相変化を受けると考えるべきです。 | |
 | でも、誘電体ではないから\(\pi\)とは限らないってことかぁ。 | |
 | そこで、\(p\)偏光の位相変化を\(\psi_p\)、\(s\)偏光の位相変化を\(\psi_s\)としているのです。一般論としては、入射光が直線偏光であっても、反射光は楕円偏光になります。 | |
 | 複素数になるだけで、ずいぶん様相が変わりますね…。 | |
 |
例えば、入射光の直線偏光が入射平面に対して方位角\(\alpha^{\left(i\right)}\)だけ傾いている場合、
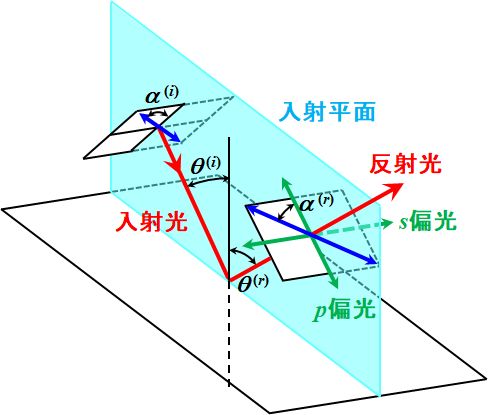 図2.5.1 直線偏光の方位 反射光の方位角\(\alpha^{\left(r\right)}\)との間には、 \[ \begin{align*} \tan \alpha^{\left(r\right)} = \frac{ {a_s}^{\left( r \right)} }{ {a_p}^{\left( r \right)} } = \frac{ \cfrac{ {a_s}^{\left( r \right)} }{ {a_s}^{\left( i \right)} } \times {a_s}^{\left( i \right)} }{ \cfrac{ {a_p}^{\left( r \right)} }{ {a_p}^{\left( i \right)} } \times {a_p}^{\left( i \right)} } = \frac{ r_s }{ r_p } \frac{ {a_s}^{\left( i \right)} }{ {a_p}^{\left( i \right)} } = \frac{ r_s }{ r_p } \tan \alpha^{\left(i\right)} \\ \end{align*} \] \[ \begin{align*} \Leftrightarrow \quad \frac{ 1 }{ \tan \alpha^{\left(r\right)} } &= \frac{ r_p }{ r_s } \frac{ 1 }{ \tan \alpha^{\left(i\right)} } = \frac {\rho_p \mathrm{e}^{i \psi_p}}{\rho_s \mathrm{e}^{i \psi_s}} \frac{ 1 }{ \tan \alpha^{\left(i\right)} } = P \mathrm{e}^{i \psi} \frac{ 1 }{ \tan \alpha^{\left(i\right)} } \tag{2.5.19} \\ &= - \frac{ \tan \left( \theta_1 - \theta_2 \right) }{ \tan \left( \theta_1 + \theta_2 \right) } \div \frac{ \sin \left( \theta_1 - \theta_2 \right) }{ \sin \left( \theta_1 + \theta_2 \right) } \frac{ 1 }{ \tan \alpha^{\left(i\right)} } \\ &= - \frac{ \sin \left( \theta_1 - \theta_2 \right) \cos \left( \theta_1 + \theta_2 \right) }{ \sin \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 - \theta_2 \right) } \times \frac{ \sin \left( \theta_1 + \theta_2 \right) }{ \sin \left( \theta_1 - \theta_2 \right) } \frac{ 1 }{ \tan \alpha^{\left(i\right)} } \\ &= - \frac{ \cos \left( \theta_1 + \theta_2 \right) }{ \cos \left( \theta_1 - \theta_2 \right) } \frac{ 1 }{ \tan \alpha^{\left(i\right)} } \tag{2.5.20} \end{align*} \] が成立します。但し、 \[ P \equiv \frac {\rho_p}{\rho_s} \tag{2.5.21} \] \[ \psi \equiv \psi_p - \psi_s \tag{2.5.22} \] です。 |
|
 | \(\cfrac{1}{\tan\alpha^{\left(r\right)}}\)は、2とおりの表記方法があるわけですね。これ、\(\theta_1=0\)のとき\(\theta_2=0\)だから、 \[ \tan \alpha^{\left(r\right)} = - \tan \alpha^{\left(i\right)} \] になりますよね。 | |
 | 垂直入射の場合、\(\alpha^{\left(r\right)}=-\alpha^{\left(i\right)}\)、つまり入射光と反射光の方位角は\(180^{\circ}\)変化していると言えます。 | |
 | ん??直線偏光が\(180^{\circ}\)回転したら、元に戻るのでは?? | |
 | というわけで、垂直入射は入射光と反射光の方位が変化しない特殊なケースの1つとなります。このとき、 \[ P = 1 \] \[ \psi = - \pi \] ということでもありますね。 | |
 | 特殊なケースの1つ??別のケースがあるってこと?? | |
 | 水平入射です。まぁ、実際は境界面すれすれに入射するってことなんですけど。 | |
 | それって、\(\theta_1=90^{\circ}\)ってこと?? | |
 | そうです。 | |
 | その場合、式2.5.20は、 \[ \frac{ \cos \left( 90^{\circ} + \theta_2 \right) }{ \cos \left( 90^{\circ} - \theta_2 \right) } = - \frac{ \sin \theta_2 }{ \sin \theta_2 } = -1 \] だから、 \[ \tan \alpha^{\left(r\right)} = \tan \alpha^{\left(i\right)} \] ですね。つまり、\(α^{\left(r\right)}=\alpha^{\left(i\right)}\)だ。 | |
 | このとき、 \[ P = 1 \] \[ \psi = 0 \] ですから、位相差も発生してない、ということになります。 | |
 | この2つが特殊ケースなのかぁ。 | |
 | 実は、もう1つ注目すべきケースがあります。 | |
 | う〜ん。式2.5.19とか式2.5.20を見ても、思い付かないですけど…。 | |
 |
では、\(P\)と\(\psi\)をグラフにしてみましょう。
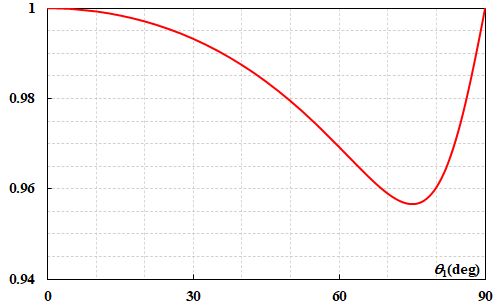 図2.5.2 \(P\)の入射角依存性(銀:\(0.20-i3.44\)) 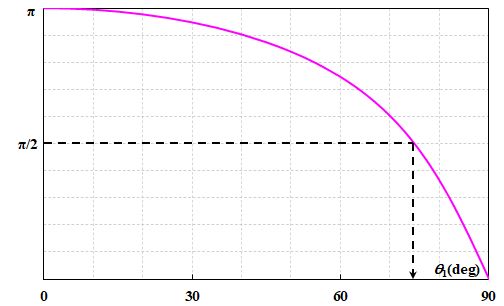 図2.5.3 \(\psi\)の入射角依存性(銀:\(0.20-i3.44\)) これを見ると、\(\psi=90^{\circ}\)になる入射角\(\theta_1\)が存在することが分かります。この入射角を主入射角と言います。 |
|
 | それが何か?? | |
 | 一般には、反射光は楕円偏光になると言いましたが、主入射角のとき、その楕円の軸が入射平面に平行及び垂直になっているということです。 | |
 | ん??とすると、\(p\)偏光と\(s\)偏光の振幅が同じだと円偏光になっているということ?? | |
 | そうです。図2.5.1から分かるように、 \[ \tan \alpha^{\left(r\right)} = \frac{ {a_s}^{\left(r\right)} }{ {a_p}^{\left(r\right)} } = \frac{ {A_s}^{\left(r\right)} \mathrm{e}^{i\phi_s}}{ {A_p}^{\left(r\right)} \mathrm{e}^{i\phi_p}} = \frac{ {A_s}^{\left(r\right)} }{ {A_p}^{\left(r\right)} }\mathrm{e}^{i\delta} \] ですから、円偏光の条件:\(A_p=A_s\)、\(\delta=\cfrac{\pi}{2}\)を考慮すると、 \[ \tan \alpha^{\left(r\right)} = i \] ですね。\(\psi=\cfrac{\pi}{2}\)なので、式2.5.19から、 \[ \frac{ P }{ \tan \alpha^{\left(i\right)} } = 1 \] である場合に、円偏光になることが分かります。 | |
 | 図2.5.2を見ると、主入射角のとき\(P\)が最低値になってますね。 | |
 | \(P\)が最低値になる入射角は準入射角と言いますが、厳密には、主入射角≠準入射角です。ただ、その差は僅かなので、ほぼ一致していると考えて構いません。 | |
 | あれ??ちょっと気が付いたんですけど、もし\(P\)の最低値が\(0\)になるとすれば、\(r_p=0\)ってことですよね??そのときの入射角はBrewster角だから、準入射角って誘電体の場合のBrewster角に対応するのでは?? | |
 |
なかなかの着眼点ですね。実際、\(n_1=1\)、\(n_2=1.5\)とすると、図2.5.2、図2.5.3のグラフは下図のように変わります。
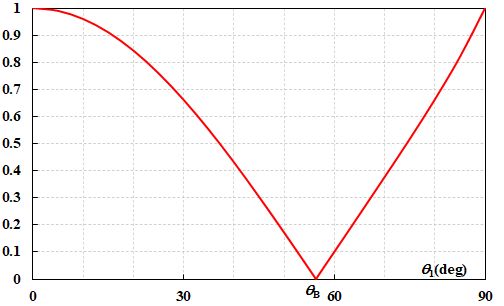 図2.5.4 \(P\)の入射角依存性(\(n_2=1.5\)) 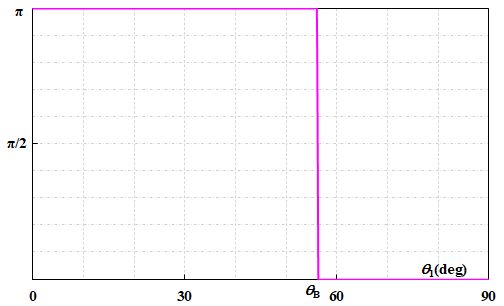 図2.5.5 \(\psi\)の入射角依存性(\(n_2=1.5\)) 確かに、\(P=0\)となる入射角はBrewster角と一致します。 |
|
 | へぇ。Brewster角の前後で、位相が\(180^{\circ}\)ずれているんですね。 | |
 | はい。ですが、直線偏光なので、実質的には何も変わってないように見えるのです。 | |
 | そう言えば、振幅のFresnel係数は嬉しくないんですよね?? | |
 |
誘電体のときと同じで、エネルギー反射率は振幅反射率の2乗だったことを思い出せば、式2.5.17と式2.5.18をそれぞれ2乗すれば計算できます。
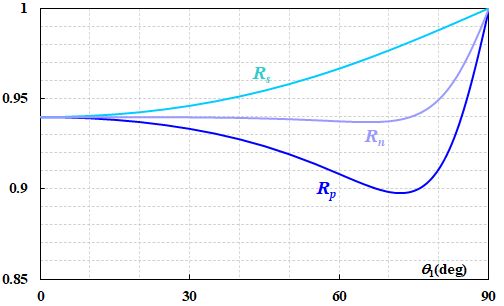 図2.5.6 エネルギー反射率(銀:\(0.20-i3.44\)) 図2.5.6は波長589.3nmにおける銀の結果です(複素屈折率:\(0.20-i3.44\))。アルミニウムや金であれば、それぞれの複素屈折率を\(1.44-i5.23\)、\(0.47-i2.83\)として、同じようなグラフを得ることができます。 |
|
 | 教授。図2.5.2〜図2.5.6って、ここでの議論だけで描けないような気がするんですけど…。 | |
 | \(\rho_p\)、\(\rho_s\)、\(\psi_p\)、\(\psi_p\)の正体を明かしてませんからね。 | |
 | それは?? | |
 | 市販されている教科書で、この形に言及しているものは見たことないですね。ただ、気になるなら、次回やることにしましょう。 |
| 前頁へ | 戻る | 次頁へ |