 | 次は式1.3.2です。 \[ \nabla \times \vec{\mathstrut E} = - \frac{ \partial \vec{\mathstrut B} }{ \partial t } \tag{1.3.2} \] これは、Faradayの(電磁誘導の)法則と呼ばれています。 | |
 | コンデンサーの静電容量の単位をF(ファラド)って言いますね。 | |
 |
はい。Faradayの名にちなんでいます。
 Michael Faraday(1791~1867) この人は存在そのものが奇跡と言えるような物理学者で、生涯の業績が凄すぎます。ちょっと列記するだけでも…。 1812年(21歳) 硫酸マグネシウムの電気分解実験 1813年(22歳) 2種類の新たな炭素塩化物の発見、Bunsenバーナーの原型を発明 1820年(29歳) C2Cl6とC2Cl4を合成、塩素の包接水和物の構成を特定 1823年(32歳) 塩素の液化に成功 1825年(34歳) ベンゼンの発見 1831年(40歳) 電磁誘導の発見 1833年(42歳) 電気分解の法則を発見 1835年(44歳) 相互誘導の発見 1837年(46歳) 静電誘導の発見 1838年(47歳) 真空放電現象の発見、発電機の製作 1839年(48歳) 電気の基本的性質の完成 1845年(54歳) 反磁性の発見、Faraday効果の発見 1847年(56歳) 金コロイドの光学特性の研究 1850年(59歳) 近接作用的概念の導入 1862年(71歳) Zeeman効果の考察 こんなにあります。 |
|
 | こ、これは…。とすると、Maxewllみたいな天才ってことですね。 | |
 | う~ん。天才は天才でしょうが、この人は子供の頃、貧乏だったので学校へ行ってないですよ。 | |
 | え、嘘??信じられない。どこで勉強したんですか?? | |
 | 14歳のとき、近所の本屋さんに年季奉公に入るんですが、働きながら立ち読みして勉強したんです。 | |
 | ますます、信じられないです。 | |
 |
だから、イギリスって不思議な国なんですよ。そして、22歳のときに運よくDavyの実験助手に雇われます。
 Sir Humphry Davy(1778~1829) で、なまじ数学の知識がなかったため、優れた洞察力と直観力だけでこれだけの発見をしたのです。 |
|
 | そう言われてみると、○○の発見っていうのが多いですね。 | |
 | 実験的な発見は、どっちかというとセンスに依るところが大きいですからね。で、この中でも、とりわけ重要なのが、初めて場という概念を導入した、という部分です。 | |
 | そう言えば前回、磁場っていうのが出てきましたね。 | |
 | はい。この概念は20世紀以降の物理学ではとても重要なもので、"場"の概念なしに宇宙論も量子論も語ることはできません。 | |
 | "場"って、何か抽象的な概念ですよね。 | |
 |
定義としては、「ある物理量を想定すると、それによって空間の様子が変化するという考え方」といったところでしょうか。質量を持った粒子の周囲の空間が歪む、という話を聞いたことありませんか??
 図1.3.8 重力場のイメージ図 |
|
 | 一般相対性理論ですね。 | |
 |
これは重力場と呼ばれる考え方になります。もちろん、重力場なんていうものは我々の目には見えません。でも、ここにもう1つの粒子を持ってくると、この歪みに沿って粒子の運動が変わってしまう。これが重力場による万有引力のメカニズムになります。
|
|
 | 日本語でも"場"の空気って言ったりしますもんね。その人が入ってくると、目には見えないけど急に緊張感が漂う、みたいな。 | |
 | イメージ的には同じです。物理学の場合は、それを数値として議論できるっていうだけの話。しかし、こういう概念を初めて導入するのには、相当柔軟な発想力が要求されると思います。例えば、学校で落ちこぼれる、と言った場合、勉強をしなくて自分から落ちこぼれるか、学校の授業が悪いので落ちこぼれるか、のどちらかを考えるのが普通で、「落ちこぼれの生ずる状況」が法則として作られている、つまり、学校というものが存在すると、その周囲の空間は落ちこぼれが生ずるように変化するのだ、とは考えないでしょう?? | |
 | う~ん、頓智みたいですね。 | |
 |
Maxwell方程式の素晴らしいのは、この"場"の考え方を数式に反映できているところです。例えば、Coulombの法則は次のような式です(\(r\)は荷電粒子間の距離、\(k\)は比例定数)。
\[
F = k \frac{ q_1 q_2 }{ r^2 }
\]
これは電荷\(q_1\)と\(q_2\)の荷電粒子による直接的な相互作用を表わして(論文)います。
 Charles-Augustin de Coulomb(1736~1806) しかし、これに対応する式1.3.3は、荷電粒子が1つ(厳密には電荷密度\(\rho\))存在すると、その周りの空間の様子が変わる(この場合は電気的な性質が変わる)のだ、と言っているわけです。 \[ \nabla \cdot \vec{\mathstrut D} = \rho \tag{1.3.3} \] これを「電場(厳密には電束密度)が生じる」と表現します。 |
|
 | そうすると、式1.3.3が意味していることは、もしもう1つの荷電粒子がやってくれば起こるであろう相互作用のお膳立てを示している、という理解でいいですか?? | |
 | そうです。そこが本質的に違う点です。この考え方の違いは、物理学に大きなパラダイム・シフトを起こすことになるんですよ。 | |
 | こういう発想をする人って、どういう頭の構造になっているのかな…。 | |
 | 凡人の想像を超えてますね。さて、Faradayの法則について見ていきましょう。この法則はAmpèreの法則の逆で、磁束密度が時間的に変化すると、その周りに電場が発生しますよ、ということを言っています。 | |
 | ん??ちょっと待ってください。磁場\(\vec{\mathstrut H}\)と磁束密度\(\vec{\mathstrut B}\)、電場\(\vec{\mathstrut E}\)と電束密度\(\vec{\mathstrut D}\)??紛らわしいのがいっぱい出てきましたね。 | |
 | ざっくり言ってしまうと、磁場と磁束密度、電場と電束密度は同じものです。しかし、厳密には違います。 | |
 | 何か、ややこしいなぁ…。 | |
 | 先ほど、"場"というのは「ある物理量を想定したときに変化する空間の様子」と言いました。一方、これに対となる"束"という概念は「"場"によって生じる流れ」というイメージです。 | |
 |
ん~、何となく分かるような。確か、Ohmの法則って、そんな感じですよね。
 Georg Simon Ohm(1789~1854) |
|
 |
あ~。それでいいんですよ。Ohmの法則(論文)は、電場\(\vec{\mathstrut E}\)によって電気の流れ\(\vec{\mathstrut j}\)(電流密度)が発生するということですからね。そして、その流れやすさが導電率\(\sigma\)と呼ばれるものです。
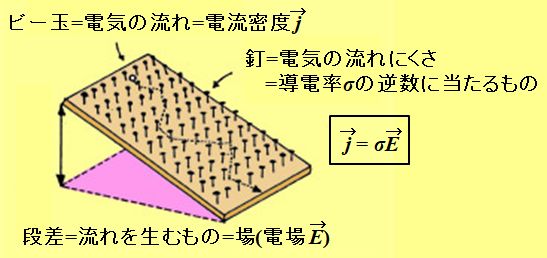 図1.3.9 Ohmの法則 式で書くとこうなりますね。 \[ \vec{\mathstrut j} = \sigma \vec{\mathstrut E} \tag{1.3.7} \] |
|
 | とすると、電場\(\vec{\mathstrut E}\)によって、電流以外にも、空間に何か流れみたいなものが生じるってこと?? | |
 | そうです。前回やったように、電流には閉回路を流れる伝導電流と、それ以外の変位電流がある、と言いましたよね。Ohmの法則は伝導電流に対応するもの、一方で変位電流に対応する流れが電束密度\(\vec{\mathstrut D}\)であり、その流れやすさが誘電率\(\varepsilon\)です。式だと、こう書けます。 \[ \vec{\mathstrut D} = \varepsilon \vec{\mathstrut E} \tag{1.3.8} \] | |
 | 磁場\(\vec{\mathstrut H}\)と磁束密度\(\vec{\mathstrut B}\)も同じことか…。 | |
 | 磁束密度と磁場の間には、透磁率\(\mu\)を使って次のような関係があります。 \[ \vec{\mathstrut B} = \mu \vec{\mathstrut H} \tag{1.3.9} \] | |
 | なるほど。この3つの式はよく似てますね。 | |
 | 式1.3.7~1.3.9をまとめて物質方程式と呼んだりします。 | |
 | そうすると、Ampèreの法則っていうのは、電気的な流れみたいなものによって磁場が発生する、ということなんですね?? | |
 | そういうイメージですね。 | |
 | 一方のFaradayの法則っていうのは、磁気的な流れみたいなものによって電場が発生する、ということか。 | |
 |
そういうことになります。さて、ここで次の動画を見てください。
|
|
 | お、磁石を動かすと電流計が反応しますね。 | |
 | はい。つまり、磁石を動かすことによって、電流計を反応させるような「何か」が発生したということです。この「何か」が電場です。 | |
 | 正確には、磁束密度の時間的な変化によって電場が発生して(Faradayの法則)、その電場によって電流密度が発生して(Ohmの法則)、それが電流計を反応させた、ってこと?? | |
 | そうですね。 | |
 | でも、電流計の反応は一瞬ですね…。 | |
 |
つまり、磁石は動き続けてないとダメなんです。そうだなぁ。ぶんぶんごまって知ってますか??
 図1.3.10 ぶんぶんごま |
|
 | あ~、子どもの頃、遊んだことありますよ。 | |
 |
この独楽の部分をネオジウム磁石に代えて、コイルの上でブンブンまわすと、LEDを点灯させることができます。
|
|
 | お~、これは面白い!! | |
 | これも、磁石が反転する瞬間は回転がストップするのでLEDが消灯してしまうんですが、何にせよ、磁束密度が時間的に変化していることがポイントです。だから、式1.3.2の右辺は\(\cfrac{\partial \vec{\mathstrut B}}{\partial t}\)なんですよ。 | |
 | マイナスの符号がありますね…。 | |
 | この符号は重要です。 | |
 | どうしてですか?? | |
 |
マイナス符号がないと仮定してみましょう(図1.3.11)。磁束密度\(\vec{\mathstrut B}_0\)を時間的に変化させるとその周りに電場\(\vec{\mathstrut E}\)が発生します(a)。そして、その電場\(\vec{\mathstrut E}\)によって電束密度\(\vec{\mathstrut D}\)が生じます。この電束密度\(\vec{\mathstrut D}\)も時間的に変化しますから、Ampèreの法則に従い磁場\(\vec{\mathstrut H}_1\)を発生させます(b)。この磁場\(\vec{\mathstrut H}_1\)によって磁束密度\(\vec{\mathstrut B}_1\)が生じます。そうすると、磁束密度\(\vec{\mathstrut B}_0\)に磁束密度\(\vec{\mathstrut B}_1\)が加わります(c)。
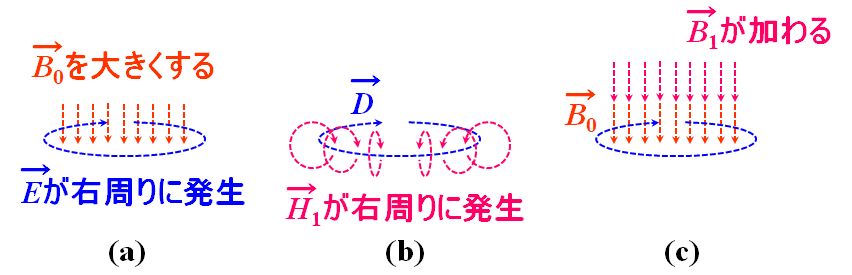 図1.3.11 Lenzの法則がなければ… |
|
 | ムムム。そのループがどんどん繰り返されて、暴走しちゃいますね。大変だ。 | |
 |
ところが、式1.3.2の右辺にマイナス符号がある(図1.3.12)ので、磁束密度\(\vec{\mathstrut B}_0\)を時間的に変化させるとその周りに図1.3.11とは逆向きの電場\(\vec{\mathstrut E}\)が発生します(a)。従って、この電場\(\vec{\mathstrut E}\)(電束密度\(\vec{\mathstrut D}\))によって発生する磁場\(\vec{\mathstrut H}_1\)(磁束密度\(\vec{\mathstrut B}_1\))は磁束密度\(\vec{\mathstrut B}_0\)と向きが逆になるのです(b、c)。
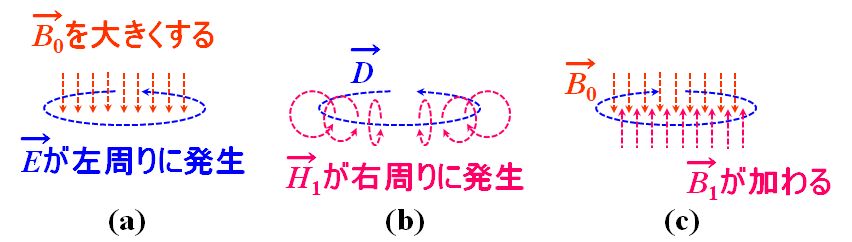 図1.3.12 Lenzの法則があるので… |
|
 | 打ち消し合うってこと?? | |
 |
そうです。つまり、暴走システムが回避されるように、この自然は設計されているということです。これをLenzの法則と言います(論文)。
 Heinrich Friedrich Emil Lenz(1804~1865) |
|
 | 上手くできてますねぇ。 | |
 |
化学の世界でも、反応が暴走しないで平衡状態になるようなシステムがありますね。Le Chatelierの原理と言いますが。
 Henry Louis le Chatelier(1850~1936) |
|
 |
磁石を動かして発生する電場も、磁石を取り囲むようにクルクルしているのかぁ。
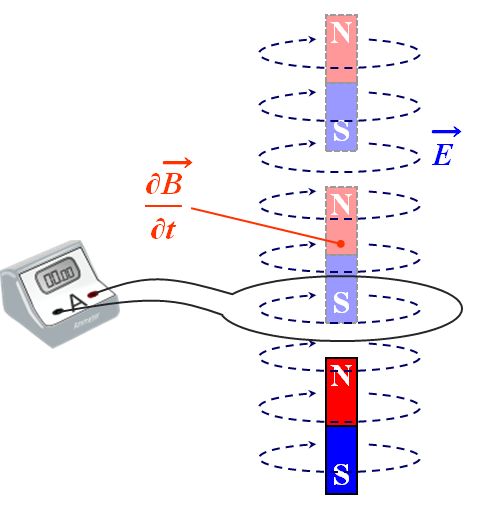 図1.3.13 磁束密度と電場の関係 |
|
 | だから、式1.3.2の左辺は\(\nabla \times \vec{\mathstrut E}\)となっているわけです。 | |
 | 電場はelectric fieldだからアルファベットの\(E\)を使うのは分かるんですけど、磁束密度って、英語ではmagnetic flux densityですよね?? | |
 |
磁束密度にアルファベットの\(B\)を用いるのは、やはり磁場の研究を先駆的に行ったJean-Baptiste Biotにちなんでます。その頭文字の\(B\)を持ってきているんですよ。
 Jean-Baptiste Biot(1774~1862) |
|
 | そう言えば、Biot-Savartの法則なんていうのがありましたね。 |
~発電のいろいろ~
 | さて、先ほどのぶんぶんごま発電は、ネオジウム磁石を回転させる駆動源は人間でした。この駆動源を別のものに代えて、磁石をもっと大きくすれば、より安定的で大きな電気を生むことができます。この駆動源を、水が流れるエネルギーとすれば、それが水力発電になります。 | |
 | お~。 | |
 |
図1.3.14は水力発電の仕組みです。
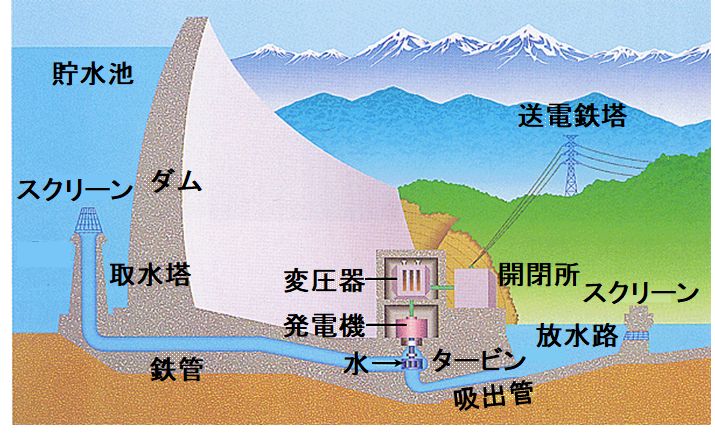 図1.3.14 水力発電の仕組み |
|
 | 鉄管を通った水がタービンを回転させて、それと連動した発電機が電気を作ると。 | |
 |
更に、その発電機は図1.3.15のような構造になっています。
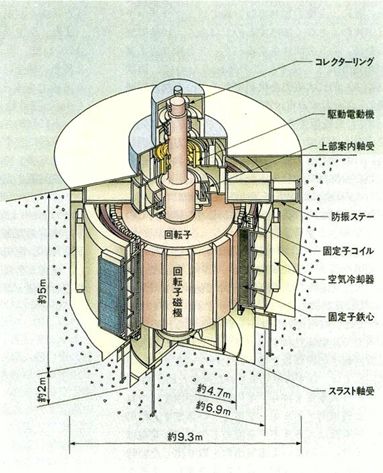 図1.3.15 発電機の仕組み |
|
 | あ、回転子磁極っていうのがたくさん並んでますね。これが、ぶんぶんごまに相当するのか。 | |
 | 基本的に、電力の発生メカニズムはすべてこれです。その動力源によって、火力発電、風力発電、潮力発電、地熱発電、原子力発電というように分類しているんですよ。 | |
 | いろいろあるけど、主流はどれですか?? | |
 |
2019年の資料によると、国内では火力発電が圧倒的ですね。
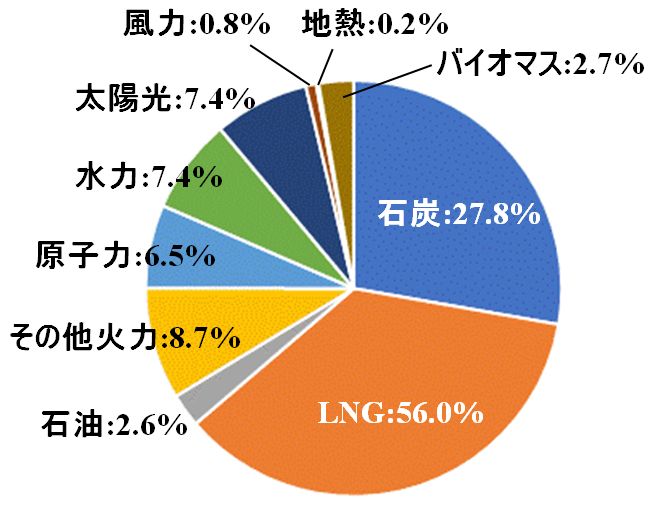 図1.3.16 国内の発電方式の内訳 |
|
 | でも、温室効果ガス(GHG)の問題がありますよね?? | |
 |
そうですね。ダントツで多いです。
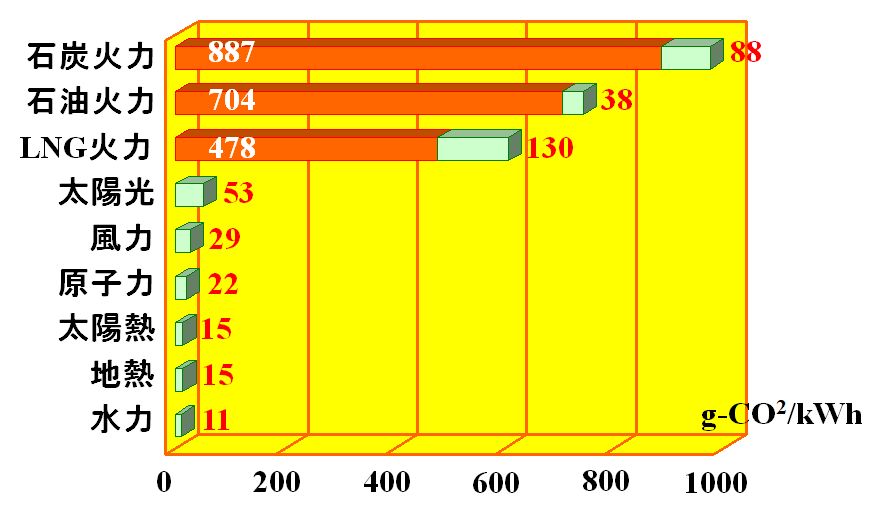 図1.3.17 発電方式別のGHG排出量 |
|
 | 橙色と緑色に分かれてますけど?? | |
 | 橙色は発電に直接的に関係する排出量、緑色は原料採掘や設備建設、燃料輸送、運輸、保守といった間接的に関係する排出量を意味します。 | |
 | 太陽光発電から水力発電までは、直接的な温室効果ガス排出量は原理的に0ってことか。 | |
 |
だから、環境に優しい方式に移行したいのですが、もう1つ考えないといけないのは単価の問題です。
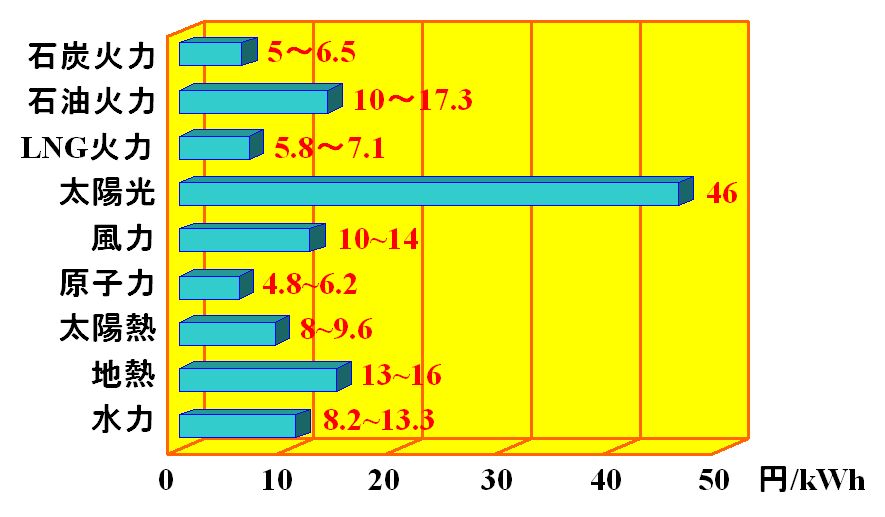 図1.3.18 発電方式別の発電単価 |
|
 | 太陽光発電がダントツですね。 | |
 | そうなんです。というわけで、図1.3.17と図1.3.18を併せて考えると、原子力発電がいいよね、という話になってしまうのです。 | |
 | でも、安全性の問題と廃棄物処理の問題があるもんなぁ。 | |
 | そこです。非常に悩ましい。 | |
 | 太陽光発電は、Faradayの法則とは無縁ですよね?? | |
 | あ、そうですね。これは半導体の性質を利用したもので、まったくメカニズムが異なります。 | |
 | 太陽なんて、ほぼ無尽蔵のエネルギー源だと思うんだけど…。 | |
 | ところが、半導体に吸収される波長帯域が限定的なので、思ったほど太陽の恵みを享受できてないんですよ。シリコン系だとか色素増感型だとか、いろいろタイプはありますが、これだけで多くの人々の生活を賄う電力を生むのは並大抵ではありません。 | |
 | 他に、もっといい発電方法があればいいんですけど…。 | |
 | 発電方法だけ見れば、いろいろ考えられます。要するに、あるエネルギーが最終的に電気エネルギーに変換されればいいわけですから。 | |
 | 例えば?? | |
 | 普通に使っている乾電池は、化学エネルギーから電気エネルギーに変換しているものですし、熱とか圧力とか摩擦とか、電気エネルギーに変換できるものはたくさんあります。 | |
 | 熱から電気?? | |
 |
Seebeck効果って言うんですけど、
 Thomas Johann Seebeck(1770~1831) 異なる金属を繋げて温度差を与えると、電圧差が発生(論文)します。それを利用するんですよ。 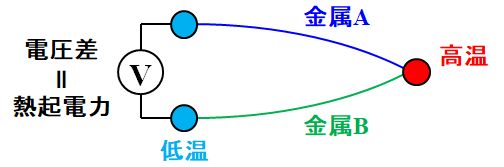 図1.3.19 Seebeck効果 例えば、温度を測定するとき熱電対を使ったこと、ありませんか?? |
|
 |
あ~、この前の測定で使いました。
 図1.3.20 熱電対 |
|
 | それがSeebeck効果の最たる応用例です。 | |
 | これ、使っているうちに、金属どうしの接合点がよく取れちゃうんですよね。 | |
 | その場合は、半田で修理すれば問題ないですよ。最悪、金属どうしを縒っちゃえばいいですし。それよりも、熱電対を使用する場合は、何の金属が接合されているのか、チェックしないといけません。 | |
 | え??そうなんですか?? | |
 | そりゃそうですよ。対になる金属の種類によって発生する熱起電力は違いますからね。K型とかT型のようなタイプがあるので、その確認が必要です。そもそも、熱電対のレコーダー側に、そのタイプをセットする項目があるでしょう。 | |
 | え~、この前の測定、ひょっとしたら全部やり直しだ~。 | |
 |
しかも、タイプごとに適用温度範囲が違うから、どんな温度でも1タイプの熱電対でカバーできると思ったら大間違いです。
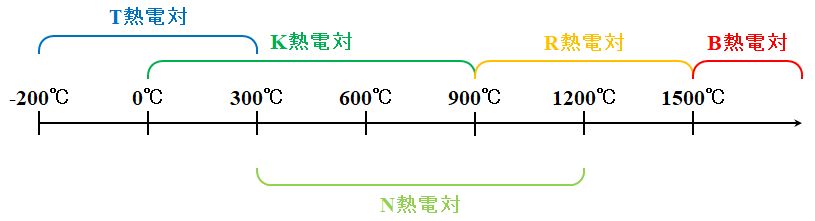 図1.3.21 熱電対のタイプと適用温度範囲 |
|
 | 後でチェックしとかなきゃ…。 | |
 | お願いします。 | |
 | 教授。電圧差を与えたら温度が発生するみたいな、逆パターンはできるんですか?? | |
 |
エネルギーの変換は一方通行ではないので、当然できます。それはPeltier効果と言いますね(論文)。
 Jean-Charles Peltier(1785~1845) パソコンのCPUを冷却するのにPeltier素子が使われてますよ。  図1.3.22 Peltier素子 |
|
 | 圧力から電気は?? | |
 |
ピエゾ効果って言うんですけど、圧力を与えると電圧が発生する材料が存在します。
圧電素子を指で押さえるだけで、LEDが点灯するのが分かるでしょう?? |
|
 | どんな材料ですか?? | |
 |
いろいろありますが、圧倒的によく利用されるのは、1952年に白根元先生が発見したチタン酸ジルコン酸鉛(論文)ですね。PZTの呼び方で知られていると思います。
 白根元(1924~2005) |
|
 | あれ??でも鉛が使われている?? | |
 | そうです。なので、現在は鉛フリーの圧電素子の開発に関心が集まってます。中でもPZTに特性が近い ニオブ酸ナトリウムカリウム(論文)が注目されていますね。KNNの方が一般的かな。これも日本人が発見したんですよ。 | |
 | ピエゾ効果も、電気から圧力という逆パターンがあり得るんですね?? | |
 |
はい。電圧を与えると変形するので、この性質を利用して、インクジェット・プリンタのインクを吐出させたりもしています。
|
|
 |
摩擦は分かります。これですよね??
 図1.3.23 摩擦帯電 |
|
 |
そうですね。少し前に、摩擦帯電を利用した発電ゴムなんていうのも開発されました。
 図1.3.24 発電ゴム |
|
 | へぇ。これ、いいじゃないですか。靴底に仕掛けておけば、歩いているだけで、スマホの充電ができそうですよ。 | |
 | 詳細の理屈については未解明な部分があるんですが、シリコーン・ゴムに電子線を照射するとE'センターという欠陥構造が作られます。そうすると、摩擦帯電しやすくなるようですね。ただ、残念ながらスマホの充電には使えません。 | |
 | え~、何でですか?? | |
 | 取り出せる電力が小さいからです。たぶん、1日3億歩くらい歩かないと充電できないですよ。 | |
 | ん??3億歩?? | |
 | 9km/hで歩いたとして、1分間の歩数は90歩くらいですから―。 | |
 | 2時間で1万歩か…。あれ、ちょっと待って…。3億歩だと60,000時間?!?!24時間で充電するにしたって、22,500km/hで歩かないといけない?? | |
 |
図1.3.25みたいなイメージですかね。
 図1.3.25 22,500km/hで走る?? |
|
 | そんなの無理ですよ~。 | |
 |
振動源はいくらでもあるんですが、朝のラッシュ・アワーのエネルギーを利用しても、それを電気エネルギーに変えたところで、使える用途は極めて限定的と言わざるを得ません。
 図1.3.26 この振動を電気に変換しても… |
|
 |
残念です…。あ、電池と言えば、2019年に吉野先生がノーベル化学賞を受賞しましたね。
 吉野彰(1948~) |
|
 |
Liイオン電池ですね。2次電池の開発は、たいてい自動車の電動化ブームとリンクしているようです。最初の大きなブームは、大気汚染が問題化した1970年にアメリカで導入されたMuskie法がきっかけでしょう。このときEVに実装されたのが、Plantèによって発明されたPb蓄電池です。
 Gaston Plantè(1834~1889) |
|
 | でも、流行らなかったですね。 | |
 |
Pb蓄電池はパワーがないからですよ。一方、ガソリン車は三元触媒といった優れた解決手段が開発されて、勢いを盛り返すのです。 次のブームは、1998年のZEV規制がきっかけです。このとき主流になったのはNi-H2充電池ですね。この電池は、Jungnerの発明したNi-Cd蓄電池を改良したものです。  Ernst Waldemar Jungner(1869~1924) |
|
 | 実績はあるんですか?? | |
 |
トヨタ自動車㈱のRAV4とか、プリウスに採用されてます。
 図1.3.27 RAV4 現在は3度目のブームで、きっかけは2005年の京都議定書の発効ですね。これで一躍脚光を浴びたのがLiイオン電池です。三菱自動車工業㈱のi-MiEVに初めて搭載されました。  図1.3.28 i-MiEV |
|
 | 環境問題も含めて、EVが主流になるといいですね。 | |
 |
こうやって考えると、Faradayの発見が、どれだけ人類に大きな貢献をしているかが分かりますね。Faradayが初めて電磁誘導の法則を公開実験したときに、当時首相だったGladstoneから「磁石を使ってほんの一瞬電気を流してみたところで、それがいったい何の役に立つのかね」と笑われたんですが、Faradayは「20年も経てば、あなたがたはその電気に税金を掛けるようになるでしょう」と答えたという逸話があります。
 William Ewart Gladstone(1809~1898) |
|
 | FaradayとMaxwellは面識があったんですか?? | |
 | 当然ですね。ちょうどFaradayの晩年とMaxwellの若い頃が年代的にダブっています。で、FaradayはMaxwellの数学的才能に惚れ込んで、それまでの物理学者たちの業績を定式化するようMaxwellに託すんです。それを見事に現実化したのが4つのMaxwell方程式なんですよ。 |
| 前頁へ | 戻る | 次頁へ |