 | 次は式1.3.3です。 \[ \nabla \cdot \vec{\mathstrut D} = \rho \tag{1.3.3} \] これは、Gaussの法則と呼ばれています。 | |
 | 前回も登場しましたね。 | |
 |
Gaussの名前は、ご存知とは思いますが、
 Johann Carl Friedrich Gauß(1777〜1855) この人も生涯の業績が凄いですね。主なものだけを抜粋しても、 1780年( 3歳) 父親の帳簿の計算間違いを指摘 1781年( 4歳) 酒樽の求積法の概念に到達 1784年( 7歳) 等差数列の和の公式を導出 1792年(15歳) 素数定理の予想 1795年(18歳) 最小二乗法の発見 1796年(19歳) 平方剰余の相互法則の証明、コンパスと定規で正17角形を作図できることを証明 1797年(21歳) 楕円関数の研究、レムニスケート関数の発見 1799年(22歳) 代数学の基本定理の証明(学位論文) 1800年(23歳) 一般楕円関数の発見、モジュラー関数の発見 1801年(24歳) 『整数論の研究』出版、自然数の素数による一意分解の定理を証明 1805年(28歳) 高速Fourier変換を定式化 1807年(30歳) ゲッティンゲンの天文台長就任、Gauss式レンズの設計、最小拘束の原理の発見 1809年(32歳) 『天体運行論』出版、最小二乗法を用いたデータ補正の方法確立、正規分布の研究 1811年(34歳) 複素積分の研究、複素数平面の確立 1818年(41歳) 正規分布の研究、Gauss-Krüger図法の考案 1827年(50歳) 『曲面の研究』出版、微分幾何学を創始 1831年(54歳) 電磁気学におけるGaussの定理、Gaussの法則の発見 ご覧のとおり。ま、正真正銘の"数学の帝王"と呼んでいいでしょう。 |
|
 | え〜っと、4歳で積分、ですか…。怪物ですね…。 | |
 | Gaussはしばらく言語学者になるか数学者になるか悩んでいたんですが、19歳のときに正17角形が定規とコンパスのみで作図できることを証明して、数学者になる決心をします。 | |
 | どうやったら証明できるのか、想像もつかないです。 | |
 | そうですね。まず、「定規とコンパスのみで作図できる」ということを数学の言葉に翻訳しないといけませんが、それがチンプンカンプンだと思います。 | |
 | 17なんて、素数だから割り切れないんですけど…。 | |
 | でも、作図可能なんですよ。64手かかりますけどね。で、Gaussはあまりにも厳格な人物だったゆえに、厳密な証明の与えられていないアイデアは絶対に世の中に発表しようとはしなかったことでも有名です。アイデアは全部、日記に書き留められていて、Gauss以後の数学者は、自分の発見が本当に世界初かどうか、Gaussの日記を調査してから発表しなければならない、というような時代が長く続くことになります。 | |
 | それはそれで迷惑ですね。 | |
 | しかも、日記は暗号で書かれてますし。 | |
 | 困ったもんだ。 | |
 |
Gaussの法則が言っていることは簡単で、空間中に電荷密度\(\rho\)が存在すると、そこから電束密度が発生する、ということを意味しています。
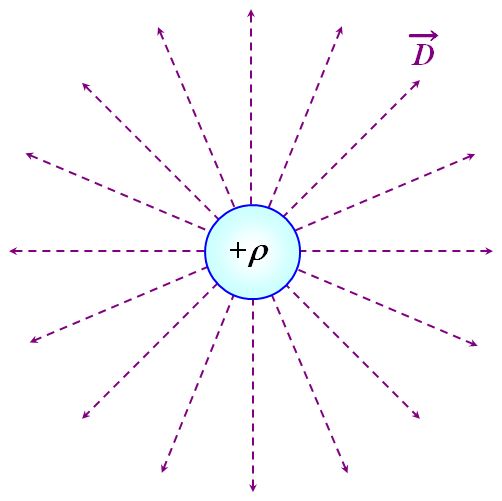 図1.3.29 電荷密度と電束密度の関係 |
|
 | 電荷密度って、英語でcharge densityですけど?? | |
 | 電荷密度は、表面電荷密度と空間電荷密度の2つがあるんですが、ここで言っている電荷密度は空間電荷密度の方です。そして、空間はドイツ語でRaum。アルファベットの\(r\)はギリシャ文字の\(\rho\)なので、\(\rho\)で表すことが多いですね。 | |
 | ドイツ語とは、いきなりの変化球ですね。 | |
 | ちなみに、式1.3.3の左辺にある\(\nabla\)・は\(\mathrm{div}\)とも書きますから―。 | |
 | 電束密度が四方八方に飛び出ているイメージかぁ。 | |
 | そういうことです。電荷密度がプラスのときは湧き出すイメージ、マイナスのときは吸い込まれるイメージです。 | |
 | なるほど〜。イメージしやすい。 |
〜磁束保存の法則〜
 | 最後は式1.3.4です。 \[ \nabla \cdot \vec{\mathstrut B} = 0 \tag{1.3.4} \] | |
 | 式1.3.3とよく似てるけど、右辺が\(0\)ですね。 | |
 | イメージできますか?? | |
 | う〜ん。式1.3.3は、電束密度を発生させる電荷密度が存在するってことだから、そのアナロジーで考えると、磁束密度を発生させる磁荷密度は存在しない、ってこと??でもなぁ。磁石の場合はN極とかS極とか言いますよね?? | |
 | 惜しいですね。\(0\)の解釈の問題です。まず、電荷密度を囲む閉曲面を想定してください。そうすると、図1.3.29は、電荷密度がプラスのとき、閉曲面のどこをとっても、電束密度は閉曲面の内から外への流れを作っていることになります。一方、電荷密度がマイナスのときは、閉曲面のどこをとっても、電束密度は閉曲面の外から内への流れを作る。では、その閉曲面内にプラスの電荷密度とマイナスの電荷密度が同時に存在すると?? | |
 |
プラス・マイナスで\(0\)になりますね。そうすると、式1.3.4は、N極とS極は同時に存在していて、それを囲む閉曲面の磁束密度はプラス・マイナスで\(0\)ってこと??
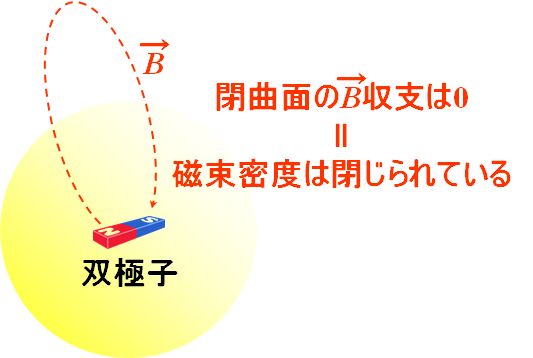 図1.3.30 磁束密度に関するGaussの法則 |
|
 |
そういうことです。つまり、電気と磁気の決定的な違いは、 ・電気の場合、異なる符号の電荷密度は単独で存在する ・磁気の場合、異なる符号の磁荷密度は単独で存在しない という点です。電荷は単極子、磁荷は双極子と言いますが、双極子の作る流れは閉じられている。これを磁束保存の法則と言います。 |
|
 | そう言えば、この世の中にモノポールは存在しないって聞いたことありますね。そうか、式1.3.4があるから存在しないのか。 | |
 | 逆です。 | |
 | 逆?? | |
 | 式1.3.4があるからモノポールが存在しないのではなく、モノポールが存在しないから式1.3.4のように記述するのです。 | |
 | ということは、もしモノポールが発見されたら?? | |
 | Maxwell方程式の方を修正しないといけません。例えば、2014年1月のNatureに、モノポールの振る舞いに関する論文(論文)が掲載されましたが、こういう研究ではMaxwell方程式は役に立ちません。 | |
 | その場合は?? | |
 |
すでに、その方程式はDiracによって用意されて(論文)います。
 Paul Adrien Maurice Dirac(1902〜1984) |
|
 | そうなのか。 | |
 | さて、以上でMaxwell方程式の意味については終了です。復習のために再掲しておくと、 \[ \nabla \times \vec{\mathstrut H} = \vec{\mathstrut j} + \frac{ \partial \vec{\mathstrut D} }{ \partial t } \tag{1.3.1} \] \[ \nabla \times \vec{\mathstrut E} = - \frac{ \partial \vec{\mathstrut B} }{ \partial t } \tag{1.3.2} \] \[ \nabla \cdot \vec{\mathstrut D} = \rho \tag{1.3.3} \] \[ \nabla \cdot \vec{\mathstrut B} = 0 \tag{1.3.4} \] そして、物質方程式がありましたね。 \[ \vec{\mathstrut j} = \sigma \vec{\mathstrut E} \tag{1.3.7} \] \[ \vec{\mathstrut D} = \varepsilon \vec{\mathstrut E} \tag{1.3.8} \] \[ \vec{\mathstrut B} = \mu \vec{\mathstrut H} \tag{1.3.9} \] | |
 | 教授。誘電率の\(\varepsilon\)はelectricの\(e\)をギリシャ文字にしたもの、透磁率の\(\mu\)はmagneticの\(m\)をギリシャ文字にしたものなんでしょうけど、導電率の\(\sigma\)は?? | |
 |
これは、電気工学者のSiemensにちなんでます。頭文字の\(S\)のギリシャ文字を持ってきて\(\sigma\)です。
 Ernst Werner von Siemens(1816〜1892) |
|
 | コンダクタンスの単位はS(ジーメンス)か。物理学系の単位って、人の名前が多いですね。 | |
 | そうですね。 | |
 | もし、日本人の武者小路とかいう名前の人が新しい法則を発見して、新しい単位を導入したら、M(ムシャノコウジ)になったりするんですかね?? | |
 |
あり得ると思いますよ。実際、原子核物理の世界では、1fm=1015mを1Y(ユカワ)と呼んだこともありますしね。もちろん、日本人で初めてノーベル物理学賞をとった湯川秀樹先生にちなんだ単位です。
 湯川秀樹(1907〜1981) |
|
 | へぇ。寿限無寿限無じゃなくてよかったですね。 | |
 | …。では、次回からMaxwell方程式を使った議論を進めていきましょう。 | |
 | お手柔らかに〜。 |
| 前頁へ | 戻る | 次頁へ |