 | さて、Mawell方程式を1つ1つ見ていきましょう。まず、式1.3.1です。 \[ \nabla \times \vec{\mathstrut H} = \vec{\mathstrut j} + \frac{ \partial \vec{\mathstrut D} }{ \partial t } \tag{1.3.1} \] これは、Ampèreの法則と呼ばれています(論文)。 | |
 | 電流の単位をA(アンペア)って言いますね。 | |
 |
はい。Ampèreの名にちなんでいます。
 Andrè-Marie Ampère(1775〜1836) この人はフランスの物理学者で、12歳には微分積分をバリバリ計算していたという天才です。あまりにも進んだ頭脳の持ち主ゆえに、論文を発表してもその内容は誰も理解できなかったというくらいの人物ですね。 |
|
 | 天才が多いですね…。 | |
 | ただ、詐欺師に大金を騙し取られたり、黒板を拭いた布で顔を拭いちゃうというような、ちょっと抜けていたところもあったようです。 | |
 | そういうところは、教授とそっくりですね。 | |
 | …。式1.3.1ですが、Ampèreが発見したのは、 \[ \nabla \times \vec{\mathstrut H} = \vec{\mathstrut j} \tag{1.3.6} \] の部分だけです。 | |
 | 式の意味が分からないですけど?? | |
 | まず、\(\vec{\mathstrut j}\)というのは電流のことです。厳密には電流密度ですね。単位面積当たりの電流を意味します。 | |
 | ということは、電流は\(\vec{\mathstrut j}\)に断面積を掛けたもの?? | |
 |
そういうことになります。さて、ここで次の動画を見てください。
|
|
 | お、電流を流すと方位磁石が動きますね。 | |
 | つまり、電流を流すことによって、方位磁石を動かすような「何か」が発生したということです。この「何か」を磁場と言います。 | |
 |
動画からすると、電流を取り囲むように発生しているように見えますね。
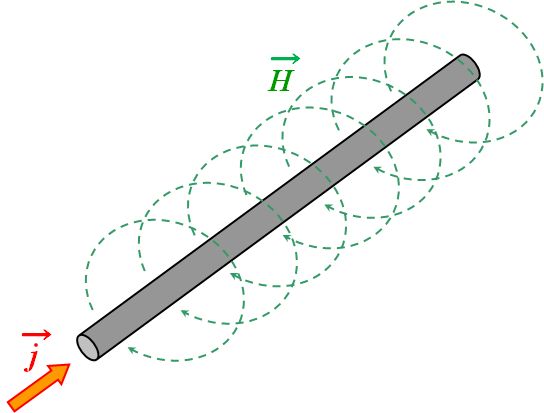 図1.3.2 電流密度と磁場の関係 |
|
 | しかも、電流の向きに応じて、その方向が変わります。ということは、磁場はベクトルで表記した方が都合がいい。だから、\(\vec{\mathstrut H}\)です。 | |
 | 磁場って、英語ではmagnetic fieldですけど、アルファベットの\(H\)なんですね。 | |
 |
これは、磁場の研究を先駆的に行ったJoseph Henryにちなんでます。頭文字の\(H\)を持ってきているんですよ。
 Joseph Henry(1797〜1878) |
|
 | 磁場の単位はH(ヘンリー)か、ふむふむ。 | |
 | また、\(\nabla \times\)は\(\mathrm{rot}\)とも書くと言いましたね?? | |
 | あ〜、なるほど。磁場がクルクル発生している様子が式で表現されているわけですね。 | |
 | そういうことです。これがAmpèreの法則の意味するところです。しかし、です。電流は、このような導線による閉回路によるものだけでしょうか?? | |
 | ん〜、どうだろ?? | |
 |
雷はどうですか??あれも電気の流れですよ。
 図1.3.3 落雷 |
|
 | お、確かに。積乱雲と地面の間には、導線がないですね。 | |
 | つまり、電流には閉回路を流れる伝導電流と、閉回路を必要としないもの、2種類が存在するわけです。そこで、Maxwellは閉回路を必要としない電流を変位電流と呼び、式1.3.6の右辺に新たな第2項として\(\cfrac{\partial \vec{\mathstrut D}}{\partial t}\)を追加したのです。これこそ、Maxwellの最大の功績と言ってもよい部分です。 | |
 | \(\vec{\mathstrut D}\)というのは?? | |
 | 電束密度です。 | |
 | 電束密度はelectric flux densityだから、アルファベットの\(D\)なんですね。 | |
 | はい。この正体は後で触れるとして、そういうものが時間的に変化しても、\(\vec{\mathstrut j}\)と同じように磁場が発生する、というのが式1.3.1の意味するところです。 | |
 | 電気から磁石のような効果が生まれるわけですね。 |
〜地球磁場とダイナモ理論〜
 | ところで、方位磁石って、そもそも東西南北を確認するための道具ですよね。 | |
 |
そうですよ。私、ガールスカウトに参加してたから、シルバーコンパス持ってましたもん。
 図1.3.4 シルバーコンパス |
|
 | どうして、方位磁石を使うと南北の確認ができるか知ってますか?? | |
 | 地球が巨大な磁石になっているからです。そんなの小学生でも知ってますよ。 | |
 | では、なぜ地球は巨大な磁石になっているんでしょうか?? | |
 | え??ん〜と、ん〜と、巨大な棒磁石が…埋まって…いる…わけ…ないか…。 | |
 | Ampèreの法則を使うと、そのメカニズムが理解できます。 | |
 | 何と!! | |
 |
地球の内部は、図1.3.5のような構造になっています。
 図1.3.5 地球の内部構造 |
|
 | 見た人、いるんですか?? | |
 | もちろん、いません。地震波などの研究を積み重ねた推測です。科学者によっては、地球の内部については太陽以上によく分からない、と指摘する人もいます。しかし、概ねこの構造に関してはオーソライズされているようですね。 | |
 | 地殻、マントル、外核、内核の4層構造ですね。 | |
 |
少なくとも、地殻とマントルの間にMohorovicić不連続面という境界があること、
 Andrija Mohorovicić(1857〜1936) マントルと外核の間にGutenberg不連続面という境界があること、  Beno Gutenberg(1889〜1960) 外核と内核の間にLehmann不連続面という境界がある(論文)ことは間違いないと言われています。  Inge Lehmann(1888〜1993) |
|
 | 地震波から、いろいろなことが分かるんですね。 | |
 | そして、外核は、放射性物質による熱と周辺部からの圧力によって高温高圧になっている。だから、その主成分と考えられている鉄やニッケルは、ドロドロに融けた液体状態になっていると予想されます。 | |
 | なるほど。 | |
 |
更に、地球は自転してますから、液体金属もグルグルと回転している。これが電流の元になり―。
|
|
 | Ampèreの法則に従って地磁気が生じていると。お〜、凄い!! | |
 |
これをダイナモ理論と言います。1946年にWalter Elsasserが提唱した理論(論文)ですよ。
 Walter Maurice Elsasser(1904〜1991) ちなみに、地球磁場は弱くなったり強くなったりしていて、60万年に1回の割合でN極とS極がひっくり返ることが知られています。 |
|
 | そんなことまで分かるんですか?? | |
 |
これを提唱したのは日本人の松山基範先生です。
 松山基範(1884〜1958) 兵庫県の玄武洞で岩石の残留磁化を測定し、1929年に世界で初めて唱えました(論文)。  図1.3.6 玄武洞 最初は、なかり冷ややかに受け止められていたようですが、20年くらいしてから測定方法が飛躍的に進歩して、この説が広く認められるようになったんです。 |
|
 | 日本人の地球科学に対する貢献度って大きいんですか?? | |
 |
世界有数の地震国でもありますからね。大きいと思います。それと地球物理学者で有名な寺田寅彦先生の影響もあるでしょう。
 寺田寅彦(1878〜1935) |
|
 | 夏目漱石の小説に登場する?? | |
 | 本名ではなくて、あくまでモデルとして登場するんですけどね。しかし、そのわりに日本の学校教育で地学を教えているケースは多くないです。 | |
 | 言われてみると、私は地学の教育を受けてないですね。 | |
 | そうでしょう。2019年には全国の高校で7〜8%しか授業が開設されてません。この空洞化は、やはり憂うべき事態だと思います。 | |
 | 教授は、地学の授業を受けたんですか?? | |
 | 高校、大学とで経験があります。私の印象ですが、地学を教える先生は変わり種が多いですね。 | |
 | へぇ。 | |
 |
高校のときは三輪主彦先生に教わりましたが、この先生は質問に行っても学校にいることは殆どなく、探しに行ったら近くの戸山公園で新聞紙にくるまってベンチで寝てたりする冒険家でしたしね。「新聞紙は断熱性が高く、防寒性に優れているので、君もやってみるといい」と薦められましたよ。
 三輪主彦(1944〜) |
|
 | うん。確かに変わってる。 | |
 |
大学のときは鈴木隆介先生に教わり、何度か地質学調査に同行したことがありますが、貸し切りバスの中で日本酒をしこたま飲んで、面白そうな断層を見つけるたびにバスを停めさせ、フラフラのまま岩盤を昇って地層の説明をするとかね。でも、遠すぎて説明がまったく聞こえないんですが…。
 鈴木隆介(1937〜) |
|
 | 変人ばっかりですね。 | |
 |
さて、その地磁気ですが、現在はどんな状況にあるかというと、実は年々低下している傾向にあります。
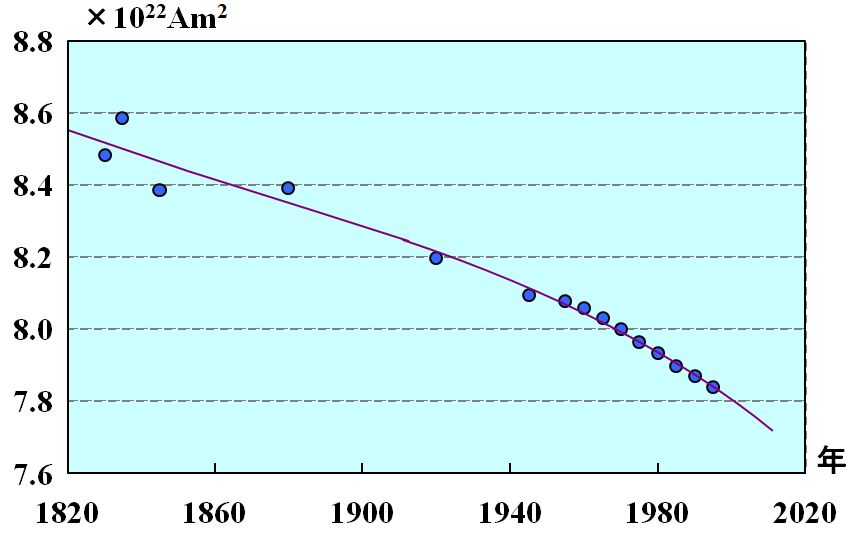 図1.3.7 地磁気の変化 |
|
 | ムムム。このままいくと、1000年後には地磁気が0になりそうですけど?? | |
 | そうですね。 | |
 | え〜。地磁気が0になると、どうなるんですか?? | |
 | 地磁気は、地球に降り注ぐ宇宙線や、太陽からの紫外線を減らす機能がありますからね。人類、或いは地球上の生命にどのような影響があるのかは、ちょっと分からないですね。 | |
 | う〜ん。とても気になりますね。 | |
 | ですが、この話を進めていくと元に戻れなくなるので、ここでやめておきます。 | |
 | な〜んだ。私はMaxwell方程式みたいな小難しい話よりも、こういうネタの方が好きなんですけど。 | |
 | 時間のあるときに調査してみるといいですよ。 |
| 前頁へ | 戻る | 次頁へ |