1.11 電磁波の伝搬

〜電磁波の伝搬〜
この章の最後に、電磁波の伝搬の様子を調べておきましょう。
いよいよ最後かぁ。
この章の、ですけど…。誘電体の中を伝搬する電磁波の電場成分は式1.4.6に帰着できましたね。 \[ \nabla ^2 \vec{\mathstrut E} = \varepsilon \mu \frac{ \partial ^2 \vec{\mathstrut E} }{ \partial t ^2 } \tag{1.4.6} \] この解を3次元の成分に分けて書いてください。
式1.1.13を使えば、振幅を\(\vec{\mathstrut E^{\left(0 \right)}}\)として、 \[ E_x = {E_x}^{\left(0\right)} \exp \big[ i \left( k_x x + k_y y + k_z z - \omega t + \phi _0 \right) \big] \] \[ E_y = {E_y}^{\left(0\right)} \exp \big[ i \left( k_x x + k_y y + k_z z - \omega t + \phi _0 \right) \big] \] \[ E_z = {E_z}^{\left(0\right)} \exp \big[ i \left( k_x x + k_y y + k_z z - \omega t + \phi _0 \right) \big] \] ですね。
では、式1.4.3の左辺を計算してみましょう。 \[ \nabla \cdot \vec{\mathstrut E} = 0 \tag{1.4.3} \]
ん〜と。 \[ \begin{align*} \nabla \cdot \vec{\mathstrut E} &= \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y} + \frac{\partial E_z}{\partial z} = i k_x E_x + i k_y E_y + i k_z E_z \end{align*} \] かな。
つまり、こうですね?? \[ \nabla \cdot \vec{\mathstrut E} = i \vec{\mathstrut k} \cdot \vec{\mathstrut E} = 0 \quad \Leftrightarrow \quad \vec{\mathstrut k} \cdot \vec{\mathstrut E} = 0 \tag{1.11.1} \]
あ、そういうことか…。
内積が\(0\)ということは??
波数ベクトル\(\vec{\mathstrut k}\)と電場ベクトル\(\vec{\mathstrut E}\)は直交している??
そうですね。まず、そのことを押さえておきましょう。次は、式1.4.2を念頭に置いて、左辺の計算です。 \[ \nabla \times \vec{\mathstrut E} = - \mu \frac{ \partial \vec{\mathstrut H} }{ \partial t } \tag{1.4.2} \]
ん〜と。 \[ \begin{align*} \nabla \times \vec{\mathstrut E} &= \left( \frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z}, \quad \frac{\partial E_x}{\partial z}-\frac{\partial E_z}{\partial x}, \quad \frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y} \right) \\ &= \left( i k_y E_z - i k_z E_y, \quad i k_z E_x - i k_x E_z, \quad i k_x E_y - i k_y E_x \right) \\ &= i \vec{\mathstrut k} \times \vec{\mathstrut E} \tag{1.11.2} \end{align*} \] かな。
一方、磁場成分は式1.4.5に帰着できました。 \[ \nabla ^2 \vec{\mathstrut H} = \varepsilon \mu \frac{ \partial ^2 \vec{\mathstrut H} }{ \partial t ^2 } \tag{1.4.5} \] よって、この解は振幅を\(\vec{\mathstrut H^{\left(0\right)}}\)として、 \[ \vec{\mathstrut H} = \vec{\mathstrut H^{\left(0\right)}} \exp \Big[ i \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \big) \Big] \] と書けます。というわけで、式1.4.2の右辺を計算してみてください。 \[ \nabla \times \vec{\mathstrut E} = - \mu \frac{ \partial \vec{\mathstrut H} }{ \partial t } \tag{1.4.2} \]
こうですね。 \[ - \mu \frac{ \partial \vec{\mathstrut H} }{ \partial t } = i \omega \mu \vec{\mathstrut H} \tag{1.11.3} \]
とすると、式1.4.2は??
こんな感じ。 \[ \vec{\mathstrut k} \times \vec{\mathstrut E} = \omega \mu \vec{\mathstrut H} \tag{1.11.4} \]
式1.11.4から分かることは、磁場ベクトル\(\vec{\mathstrut H}\)は、波数ベクトル\(\vec{\mathstrut k}\)と電場ベクトル\(\vec{\mathstrut E}\)に直交するということです。
てことは、すべてのベクトルは直交していることになりますね。
そして、波数ベクトル、電場ベクトル、磁場ベクトルの順番で右手系を構成することも分かります。というわけで、電磁波は図1.11.1のように伝搬していることになるのです。


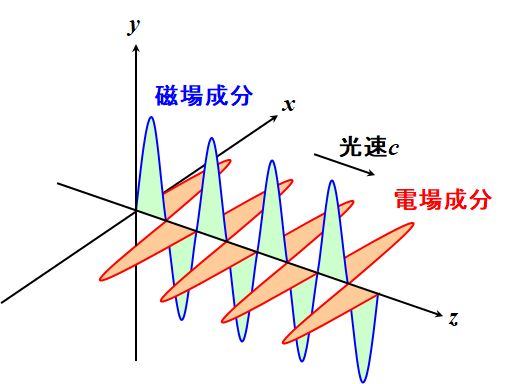図1.11.1 電磁波の伝搬
教授。よく、図1.11.2のように描かれているのを見ますけど??


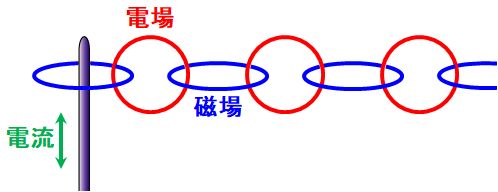図1.11.2 正しくない電磁波の伝搬
図1.11.2は、鎖が連なるように、電場→磁場→電場→磁場→…と交互に伝搬しているモデルで、とても分かりやすいですが、正しくありません。
そうだったんだ…。
また、電場成分と磁場成分の振幅の比は、式1.11.4の絶対値をとれば分かります。
\(\vec{\mathstrut \left|k\right|}=k\)、\(\vec{\mathstrut \left|E\right|}=E^{\left(0\right)}\)、\(\vec{\mathstrut \left|H\right|}=H^{\left(0\right)}\)とすれば、 \[ k E^{ \left(0\right)} = \omega \mu H^{ \left(0\right)} \tag{1.11.5} \]
ここで、式1.1.7に式1.1.9と式1.1.10を代入すると、 \[ v_p T = \lambda \quad \Leftrightarrow \quad v_p \frac{ 2 \pi }{ \omega } = \frac{ 2 \pi } { k } \quad \Leftrightarrow \quad v_p = \frac{ \omega }{ k } \tag{1.11.6} \] ですね。
そうすると式1.11.5は、 \[ \frac{ E^{ \left(0\right)} }{ H^{ \left(0\right)} } = v_p \mu \tag{1.11.7} \]
更に、媒質中の光の位相速度\(v_p\)は式1.4.7で表せました。 \[ v_p = \frac{ 1 }{ \sqrt{ \varepsilon \mu } } \tag{1.4.7} \]
そうすると式1.11.7は、 \[ \frac{ E^{ \left(0\right)} }{ H^{ \left(0\right)} } = \frac{ \mu }{ \sqrt{ \varepsilon \mu } } = \sqrt{ \frac{ \mu }{ \varepsilon } } \tag{1.11.8} \] になりますね。
つまり、式1.11.8が、電場成分と磁場成分の振幅の比を示していることになります。特に、係数の\(\sqrt{\cfrac{\mu}{\varepsilon}}\)は特性インピーダンスと呼ばれます。
インピーダンス??
直流理論での抵抗に相当する、交流理論における電流の流れにくさです。ただ、わざわざ「特性」とついてますよね??
そうですね。
なので、単純なインピーダンスとは厳密には異なります。ちなみに、インピーダンスの逆数をアドミタンスと言い、 \[ Y = \sqrt{ \frac{ \varepsilon }{ \mu } } \tag{1.11.9} \] と定義されています。
何で、電磁波の話に、交流理論の特性値が出てくるんですか??
まぁ、そこが物理学の深遠なところなんですが、ここで交流理論と同じインピーダンスという概念が出てきたことから、交流理論でも、電磁波に起こる現象がそっくり起こり得ることが予想されます。
例えば??
電磁波の場合には媒質の異なる境界面で反射が起こりますが、交流理論でもインピーダンスの異なる境界面で信号の反射が起こる、とかですね。こういう状況はインピーダンス不整合と呼ばれていて、信号の伝送の効率を著しく悪くする要因になります。このときの反射率の公式は、電磁波の公式とそっくりになりますね。
でも、交流理論は、ここでは深入りしない??
一応、光技術基礎なので、交流理論には深入りしません。従って、ここでインピーダンスとかアドミタンスとか言っても、あまり旨味はないかもしれないです。
教授。電磁波は電場成分と磁場成分のセットで取り扱わないといけないから面倒ですね。
しかし、上述の議論から、電場成分が分かれば、磁場成分の振る舞いは計算できますし、その逆もまた真です。ということは、どっちかで取り扱えば充分ということになります。
ムムム。どっちがbetterなんですか??
光について議論する場合には、圧倒的に電場成分でしょう。理由はいくつかありますが、
　@肉眼や光電検出器、写真感光材料などは光の電場成分と作用することが分かっている
　A屈折率が比誘電率の平方根で近似できる
などが、主なものでしょう。
じゃぁ、以降は電場成分だけしか登場しないってことですね。
はい。
よかった〜。手間が省けてナイスで〜す。

〜横波と縦波〜
ちなみに、波動には横波と縦波の2種類があります。
地震にも横揺れと縦揺れってありますね。
同じようなものですよ。横波はこのような伝搬をしています。

今までの電磁波は横波ってことですね。
他にもヴァイオリンの弦の振動が典型的な例です。一方、縦波はこのような伝搬をしています。


一見すると、質点が波動の伝搬方向に動いているように思えますが、実際は、その場で行ったり来たりしているだけだという点に注意してください。
横波の立ったり座ったりが、行ったり来たりに変わっているわけですね。
そうです。音波が縦波の典型的な例でしょう。粗密波と言うこともあります。
そうか。密度の高い部分が次々に送られているイメージですね。
横波と縦波の違いはいろいろありますが、1つ重要なポイントとして、それぞれの波動を正面から見たときに、質点の運動が認識できるかどうか、というのがあります。
縦波は、質点が伝搬方向を行ったり来たりしているだけだから、質点の運動は分からないですね。横波は、立ったり座ったりだから認識可能ってことか。
このような横波の特徴を偏極と言います。
横波は偏極を持っている、逆に偏極が確認できたら横波ってことでもあるわけですね。
特に、電磁波の場合は偏光と言います。そして、光が波動であるとすれば横波でなければならないということは18世紀には明らかになっていました。
それは、偏光の存在がすでに発見されていたから、ってこと??
そうです。
18世紀だと、粒子説vs波動説はどっちが優勢だったんですか??
波動説ですね。ところが、波動説を採用すると1つ厄介な問題が発生します。それは、光を伝搬させている媒質は何か、ということです。
真空でも光は伝搬するってだけの話では??
それは現代の解釈ですよ。その当時は真空という考え方はタブーだったのです。
あ〜、それでエーテルとかいう媒質を編み出したわけですね。
エーテルの概念は古代ギリシャからありました。この時代の哲学者たちが非常にこだわっていたのが、「アルケー(=万物の根源)とは何か」という問いで、それに対する答えとしてAnaximandrosが「アルケー=アペイロン(=無限なるもの)」と唱えたのがエーテルの最初だと言われています。


Anaximandros(紀元前610頃〜紀元前546)
思考の遊戯って感じもしますけどね。
でも、こういう抽象的な考察が、後に自然科学を形作っていくので、あながち遊戯と斬り捨てるわけにもいかないんですよ。さて、Anaximandrosに反論したのがParmenidēsです。この人は、「あるものはあり、あらぬものはあらぬ」という排中律的な二元論的世界観を唱えます。つまり、ないものを考えても仕方なく、空虚な空間など存在しない、と考えたのです。


Parmenidēs(紀元前520頃〜紀元前450頃)
分からないでもないですけど、別に空虚な空間を拒否しなくてもよかったのに。
恐らくですが、この頃のギリシャの哲学者たちは、0とか無限という概念を非常に嫌ったのではないかと考えられます。
どうしてですか??
分割できないからですよ。Parmenidēsの弟子にZenoという人がいますが、この人は数々のパラドックスを提唱し、0や無限を受け入れると、どれだけ奇妙なことが起こるかを示して、当時の哲学者たちを煙に巻きました。


Zeno Eleates(紀元前490頃〜紀元前430頃)
アキレスと亀みたいなやつ??
そうです。この点は「無」という概念を積極的に取り入れた東洋哲学と本質的に異なります。実際、数字の0という概念は、「無」というものが存在してもよい、と柔軟に考えるインド仏教から出てきたものなんですよ。
西と東で、まったく別の思想が醸成されていくなんて、不思議ですねぇ。
いずれにしても、Parmenidēsの「ないものはない」という考え方は、そのままAristotelēsに引き継がれ、Anaximandrosのアペイロンは、アイテールという実在するものに修正されるのです。


Aristotelēs(紀元前384〜紀元前322)
そして、Empedoclēsの提唱した「アルケー=水・土・火・空気」という四元素説にアイテールを加えた五元素説を提唱し、それがルネサンスまで影響を及ぼすようになります。


Empedoclēs(紀元前490頃〜紀元前430頃)
Aristotelēsの影響力って、凄いんですね。
このアイテールを17世紀にエーテルとして復活させたのがDescartesです。
Fermatと戦った人ですね。
Descartesは哲学者・数学者・物理学者であり、大変なマルチ・タレントだった人です。子供の頃は病弱だったんですが、通っていた学校の校長先生に気に入られて、午前中は好きなだけ寝ててよい、学校は昼から来ればよい、と言われ、朝寝の習慣が身に付いてしまいます。
いいなぁ。好きなだけ寝てていいなんて、私も一度は言われてみたいです。
しかし、この人は、その朝寝のまどろみの中で深い思索をし、空間座標の概念などを生むんですよ。
私も、夢見心地だったら、何かいいアイデアが出るかもしれないな。
…。Descartesは晩年、スウェーデンの女王Kristinaの熱烈なラブコールで家庭教師を引き受けることになります。


Kristina(1626〜1689)
ところが、このKristinaは大変な勉強家だったため、朝5時くらいから叩き起こされて講義をするという生活を強いられることになります。
うは。これはしんどいですね…。朝寝なんてできないじゃないですか。
そうです。その習慣が身に沁みているDescartesにとっては地獄の日々で、着任して1年で肺炎を起こして死んでしまいます。
え〜、それは酷い。もっと長生きしてたら、いろいろな思想が生まれてたかもしれないですよ。
そうかもしれませんが、当時の基準で54歳は高齢ですからね。
教授。Descartesは粒子説をとってたのに、エーテルを提唱したのはなぜですか??
Descartesはエーテルを非常に機械論的に考えてました。これを渦動説と言うんですが、この宇宙はエーテルと呼ばれる微小媒質で埋め尽くされており、その1つ1つは回転運動をしていると唱えたのです。この回転運動が、地球を公転させたり、光の粒子を前進させたりする、という発想ですね。
凄いイメージですね。ちょっと受け入れがたい感じもしますけど。
ところが、当時は非常に支持されたんですよ。真空なんて説明のややこしいことを考えなくていいし、機械論的な説明が受け入れられやすいベースが整っていたんでしょうね。この考え方は、万有引力を発見したNewtonによって否定されますが、Huygensのような光の波動説を指示する人たちからは、光の伝搬を都合よく説明できる媒質という位置づけで引き続き支持されるのです。
それにしても、想像逞しくいろいろ考えますねぇ。
ちなみに、コンピュータ・ネットワークの規格でイーサネットというのがありますが、イーサ(Ether)っていうのは、エーテルから取られています。
へぇ。世の中を遍くインターネットで覆ってやろうという意気込みが感じられますね。
ところが、エーテル仮説は、光は横波であるということが決定的になると、少しずつ綻びが出てきます。
例えば??
まず、横波は固体中しか伝搬しません。
ん??液体中とか気体中は伝搬しない??
しません。横波は、質点を波動の伝搬方向に垂直にずらしたときに、元に戻る復元力が存在しなければなりません。液体や気体は、その復元力が期待できないからです。液体が横波を形成するのは表面だけです。
う〜ん。てことは、私たちの周りに、エーテルという固体が埋まっているってこと??
エーテル仮説を受け入れるならば、そう考えないといけませんね。しかも、光のような高周波の波動が伝搬するためには、その固体は相当硬くないといけない。
う〜ん。それは何か無理がありますね…。
そこで本当にエーテルなんて存在するんだろうか??という疑惑が浮上してくるわけです。これを実験的に証明しようとしたのがMichelsonとMorleyの2人です。
あ〜、干渉実験ってやつですね。
実験の具体的な内容については、干渉を勉強するときに取り上げましょう。彼らは実験を通じて「エーテルが存在すると仮定したときに予想される干渉縞のずれは観測されなかった」という控えめな結論を出すのですが、これがエーテルの実在を否定する決定打となり、Einsteinが特殊相対性理論を構築するきっかけの1つになるんです。
これもノーベル賞ですか??
そうですね。エーテルの証拠をつかみ損ねた、という意味では、実験に失敗してノーベル物理学賞を受賞した極めてレアなケースと言えるでしょう。実は、Lorentzが新しい変換公式を導出したのは、「それでも尚、エーテルが存在するとしたら、どういう性質を持っているべきか」という悪あがきが動機だったのですが、逆にEinsteinがエレガントにその変換公式を導出したので、エーテルなんてなくても諸々の現象が綺麗に説明できる、というふうに全体的な考え方が変わっていくわけです。
で、結局、光を伝搬する媒質の問題はどう決着するんですか??
非常に禅問答的なんですが、「それは空間そのものである」というのがEinsteinの用意した解答です。
う〜ん。答えになっているような、なってないような…。
ま、たいていの人は納得しかねる解答だとは思いますけどね。とりあえずは、受け入れてください。

前頁へ 戻る 次頁へ