 | さて、この章から偏光です。たぶん、光学ビギナーにとって、これが最も掴みどころがない概念だと思います。 | |
 | そうなんですか?? | |
 | まぁ、すぐに分かるでしょう。まず、光の電場成分について、これが三角関数で表現できるというのはいいですね?? | |
 | はい。 | |
 |
例えば、図2.1.1のような\(zy\)平面内で振動している電場成分があったとして、これを(a)から観察したとき、その電場成分はどのように見えるでしょう??
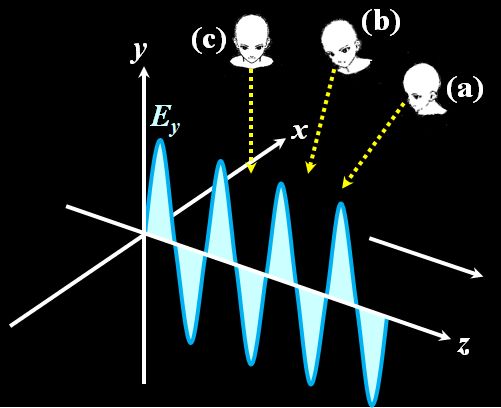 図2.1.1 見る方向でどう変わるか |
|
 | やっぱり三角関数じゃないんですか??尤も、振幅は見掛け上、小さくなっているとは思いますけど。 | |
 | そうですね。では、(b)だと?? | |
 | 同じだと思います。 | |
 | (c)ではどうでしょう?? | |
 | 直線?? | |
 | それも、振幅が\(0\)の三角関数だと考えることはできますよね。 | |
 | まぁ、そうですね。 | |
 | ということを踏まえると、ある電場成分の振る舞いを記述するには、2つの異なる方向から観察すればいい、ということも理解できますね。 | |
 | う~ん。そうか…。今まで、図2.1.1のように座標軸で張られる平面内に三角関数を描いていたけど、それは恣意的なものだということですね?? | |
 | そうです。そういう描き方は便宜的なもので、本質ではありません。 | |
 | でも、2つの異なる方向の選び方は無数にありますけど。 | |
 | というわけで、2つの方向は直交している、ということを制約条件に課しましょう。 | |
 | そうすると、改めてその2方向を\(x\)軸、\(y\)軸と定義すれば、電場成分は、 \[ E_x = A_x \cos \left( kz - \omega t + \phi \right) \] \[ E_y = A_y \cos \left( kz - \omega t + \phi \right) \] というように分解して考えるのが一般的だ、ってことですね。 | |
 | で、通常の横波であれば、ここで終了です。しかし、我々が扱っているのは光だ、ということを思い出さないといけません。光の媒質って何でしたっけ?? | |
 | Einstein流に言えば、「空間そのもの」でしたよね?? | |
 | そうです。これが通常の横波と決定的に違う点です。通常の横波は、水面の波紋にしろ、ヴァイオリンの弦の振動にしろ、地震波(S波)にしろ、観客席のウェーブにしろ、ロープを上下に振ってウネウネさせるにしろ、すべての質点の運動の方向は、必然的に同一平面内に縛られていました。ところが、光は空間そのものが媒質ですから、その自由度が異なります。 | |
 | ムムム。何かややこしくなりそうな予感。 | |
 | 実は、光を特徴づけるパラメータで、見る方向によって絶対に変わらないのは1つしかありません。 | |
 | え??ひょっとして波長?? | |
 | そのとおりです。周期は式1.1.7の関係があるので、波長が決まれば同時に決まってしまうでしょ?? | |
 | なるほど。ん??てことは初期位相は変わっていい?? | |
 | はい。光だけに許される最大の特徴と言える部分であり、光学ビギナーが最も受け入れがたいのが、この考え方ですね。 \[ E_x = A_x \cos \left( kz - \omega t + \phi_x \right) \tag{2.1.1} \] \[ E_y = A_y \cos \left( kz - \omega t + \phi_y \right) \tag{2.1.2} \] | |
 | 振幅が見る方向によって変わるのは分かるけど、初期位相が変わってもいい??ピンと来ないなぁ。 | |
 |
イメージとしては、こんな感じです。
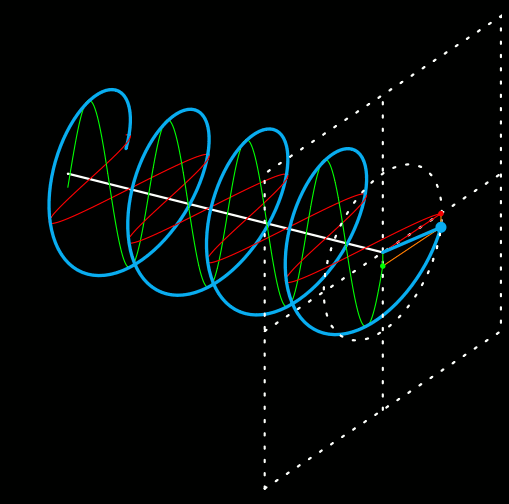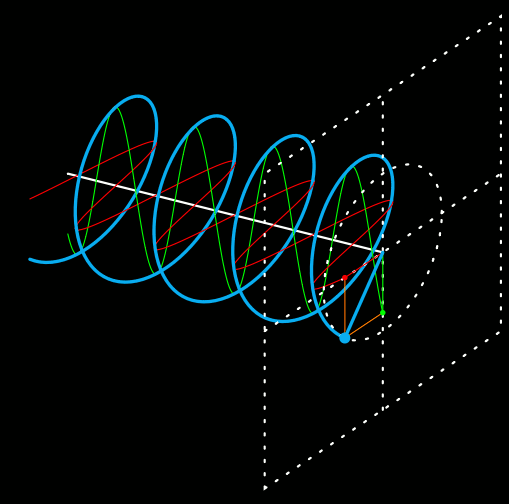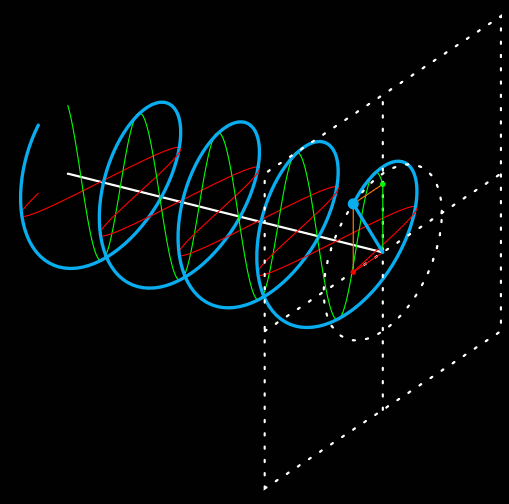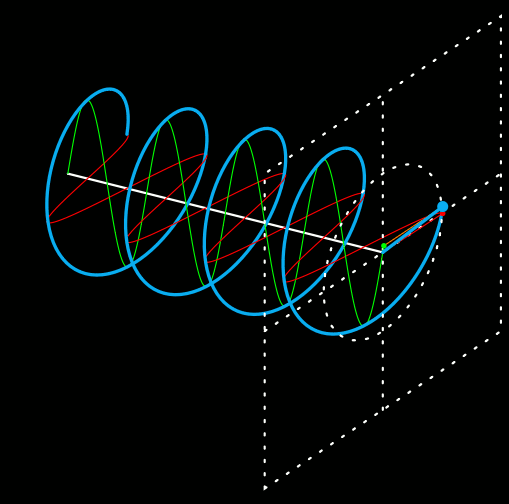 図2.1.2 偏光 上から見た三角関数が赤で、横から見た三角関数が緑で示されています。それぞれは振幅も初期位相も異なりますが、質点の運動が青色の軌跡を描くとすれば、こういう状況が成立することは理解できると思います。 |
|
 | 確かに、質点は1つの平面上ではなくて、自由に運動してますね…。 | |
 | 但し、でたらめな自由ではなく、「直交する2つの方向から観察したときに、波長が同じである三角関数として見える」という束縛は受けているわけです。そのため、規則的な螺旋状に運動することになるのです。 | |
 | こういう振る舞いは光(電磁波)だけ?? | |
 | 光(電磁波)だけでしょうね。 | |
 | すべての質点の運動が同一平面上に縛られているのは、特殊ケースってことか…。 | |
 | そうですね。それは、直交する2つの方向から観察したときに、初期位相が、 \[ \phi_y - \phi _x \equiv \delta = 0, \quad \pm \pi \] の場合のみです。 | |
 | なるほど…。 | |
 |
この条件を満たすときに、この光を正面から観察すると、質点の軌跡はある線分上を行ったり来たりしているように見えます。これを直線偏光と言います。
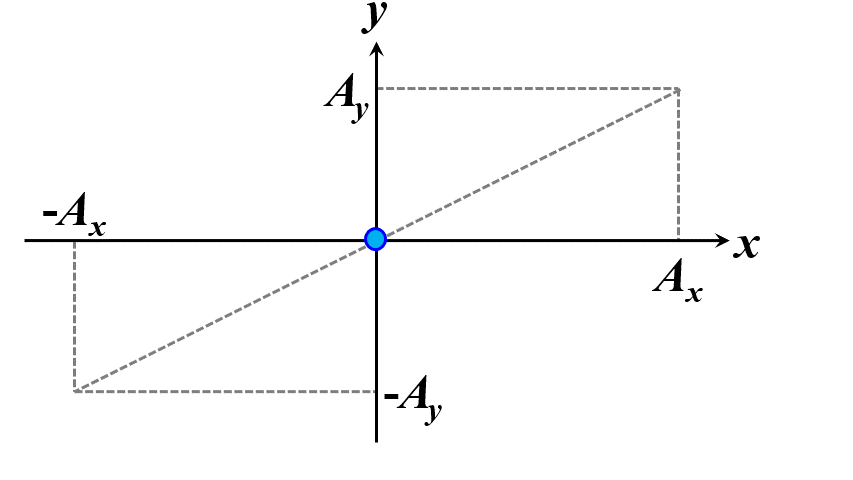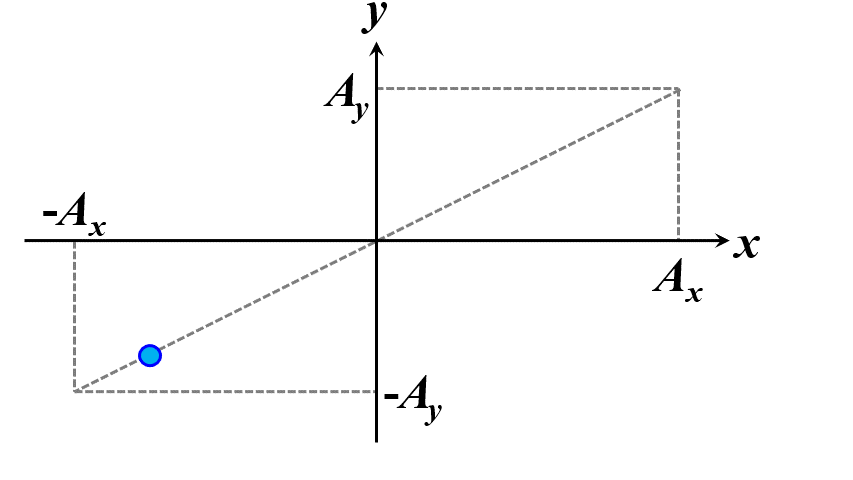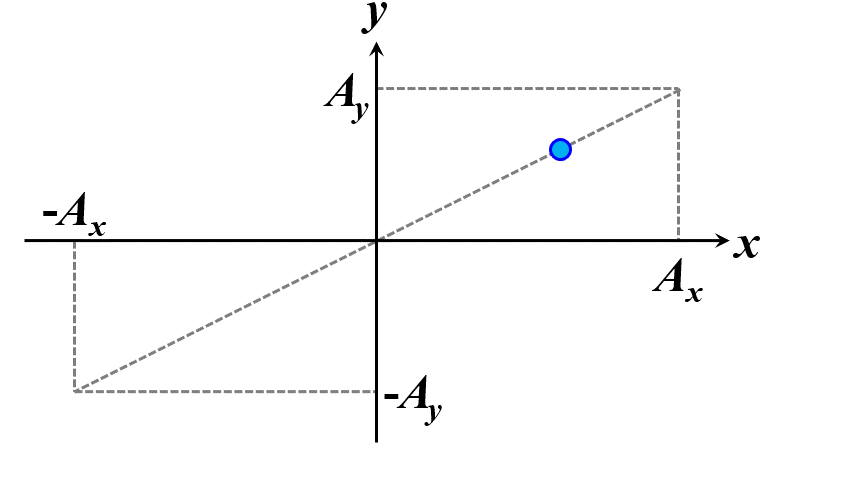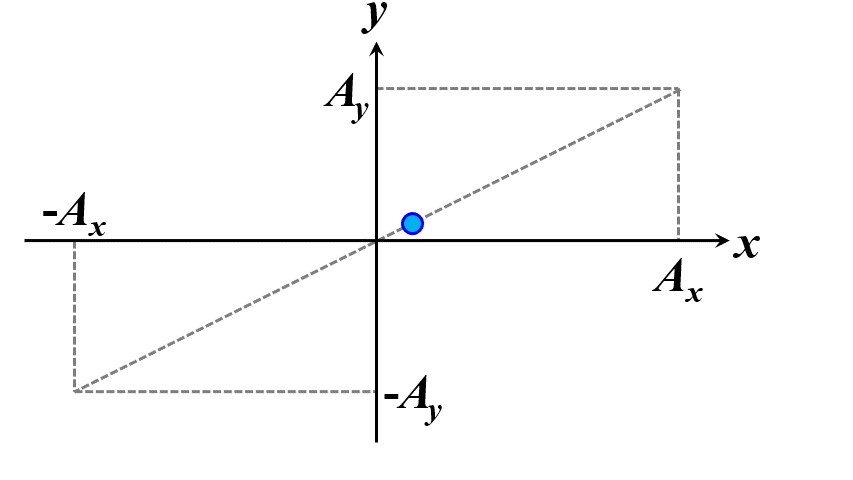 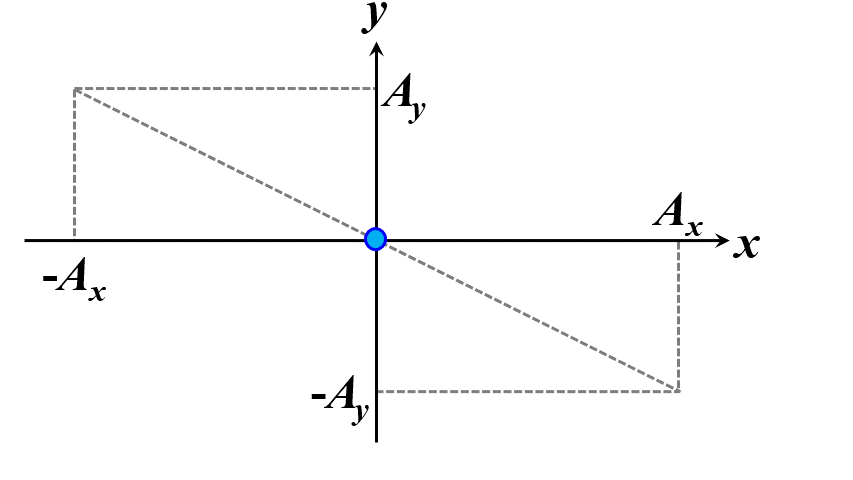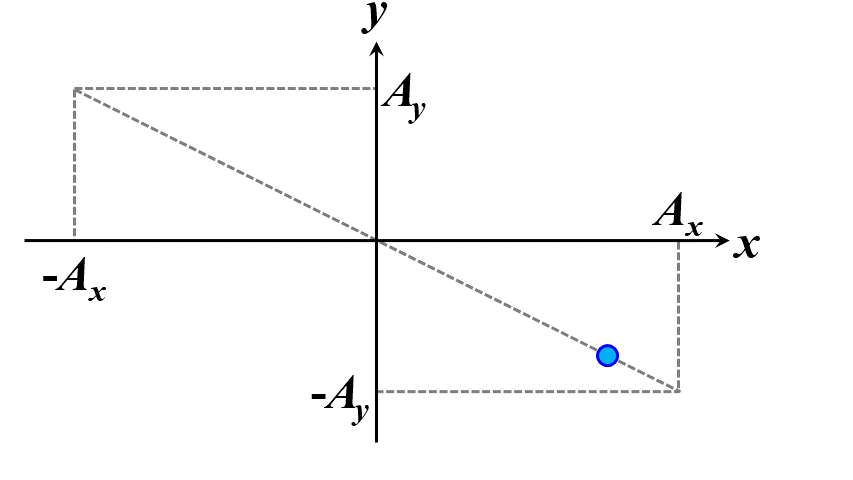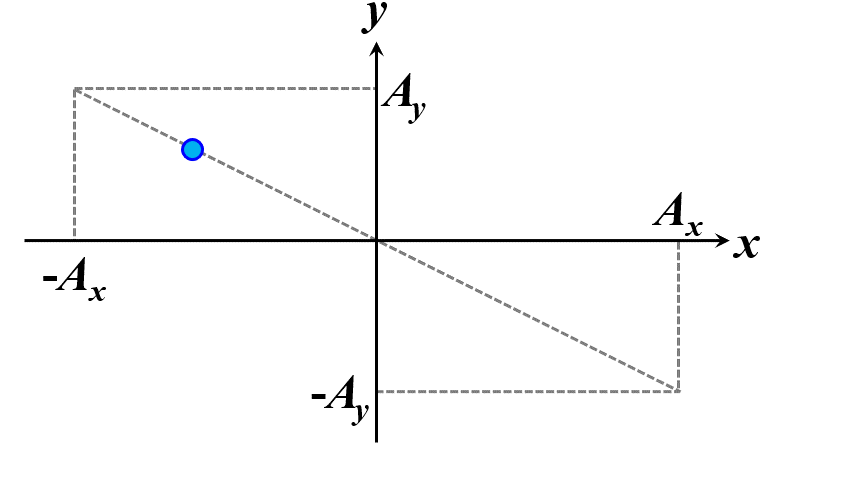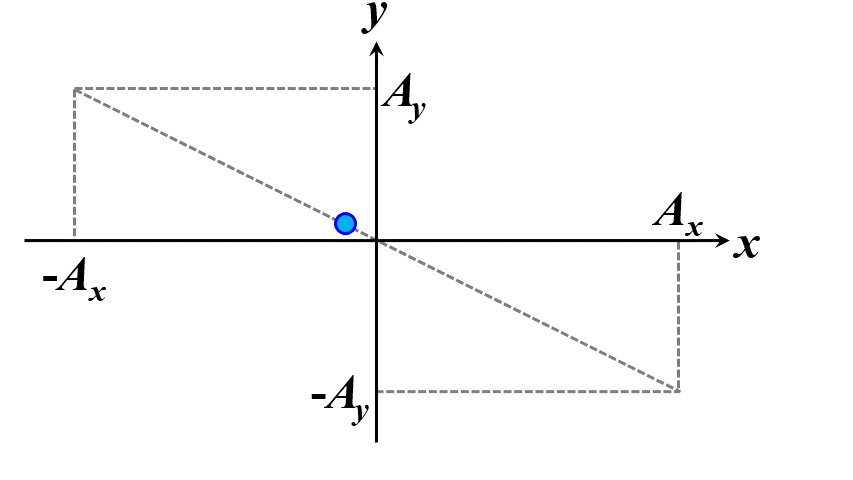 図2.1.3 直線偏光(左:\(\delta=0\)、右:\(\delta=\pm\pi\)) |
|
 | だったら、一般的には、正面から観察したときの質点の軌跡は、どう見えるんですか?? | |
 | 楕円です。それは、次のようにして証明できます。まず、式2.1.1と式2.1.2を、 \[ E_x = A_x \cos \left( kz - \omega t + \phi_x \right) \tag{2.1.3} \] \[ E_y = A_y \cos \left( kz - \omega t + \phi_x + \delta \right) \tag{2.1.4} \] としてから、式2.1.4の両辺を\(A_y\)で割った後、加法定理で展開してください。 | |
 | 加法定理…。こうだったかな…。 \[ \begin{align*} \frac{ E_y }{ A_y } &= \cos \left( kz - \omega t + \phi_x + \delta \right) \\ &= \cos \left( kz - \omega t + \phi_x \right) \cos \delta - \sin \left( kz - \omega t + \phi_x \right) \sin \delta \end{align*} \] | |
 | 右辺の第1項は、式2.1.3が代入できますよね。そのうえで、左辺に移項して、両辺を2乗します。 | |
 | う~ん。 \[ \frac{ E_y }{ A_y } = \frac{ E_x }{ A_x } \cos \delta - \sin \left( kz - \omega t + \phi_x \right) \sin \delta \\ \Leftrightarrow \quad \frac{ E_y }{ A_y } - \frac{ E_x }{ A_x } \cos \delta = - \sin \left( kz - \omega t + \phi_x \right) \sin \delta \] \[ \begin{align*} \Rightarrow \quad \left( \frac{ E_y }{ A_y } - \frac{ E_x }{ A_x } \cos \delta \right)^2 &= \sin^2 \left( kz - \omega t + \phi_x \right) \sin^2 \delta \\ &= \left[ 1- \cos^2 \left( kz - \omega t + \phi_x \right) \right] \sin^2 \delta \\ &= \left[ 1- \left( \frac{ E_x }{ A_x } \right)^2 \right] \sin^2 \delta \end{align*} \] \[ \begin{align*} &\Leftrightarrow \quad \left( \frac{ E_y }{ A_y } \right)^2 - \frac{ 2 E_x E_y }{ A_x A_y } \cos \delta + \left( \frac{ E_x }{ A_x } \right)^2 \cos^2 \delta = \sin^2 \delta - \left( \frac{ E_x }{ A_x } \right)^2 \sin^2 \delta \\ &\Leftrightarrow \quad \left( \frac{ E_y }{ A_y } \right)^2 - \frac{ 2 E_x E_y }{ A_x A_y } \cos \delta + \left( \frac{ E_x }{ A_x } \right)^2 \cos^2 \delta + \left( \frac{ E_x }{ A_x } \right)^2 \sin^2 \delta = \sin^2 \delta \\ &\Leftrightarrow \quad \left( \frac{ E_x }{ A_x } \right)^2 - \frac{ 2 E_x E_y }{ A_x A_y } \cos \delta + \left( \frac{ E_y }{ A_y } \right)^2 = \sin^2 \delta \tag{2.1.5} \end{align*} \] しんどい…。 | |
 | 式2.1.5は、\(E_x\)と\(E_y\)の2次曲線を意味しますが、判別式を計算することで、放物線か、楕円か、双曲線のいずれかが分かりますね。 | |
 | 次は判別式か…。 \[ \frac{ 1 }{ {A_x}^2 } \frac{ 1 }{ {A_y}^2 } - \left( \frac{ \cos \delta }{ A_x A_y } \right)^2 = \frac{ 1 - \cos^2 \delta }{ \left( A_x A_y \right)^2 } = \frac{ \sin^2 \delta }{ \left( A_x A_y \right)^2 } \geq 0 \] え~っと、これは―。 | |
 |
楕円ですね。つまり、このことから一般的に楕円偏光であることが証明できました。\(\delta\)の範囲で、図2.1.4のように分類することができます。
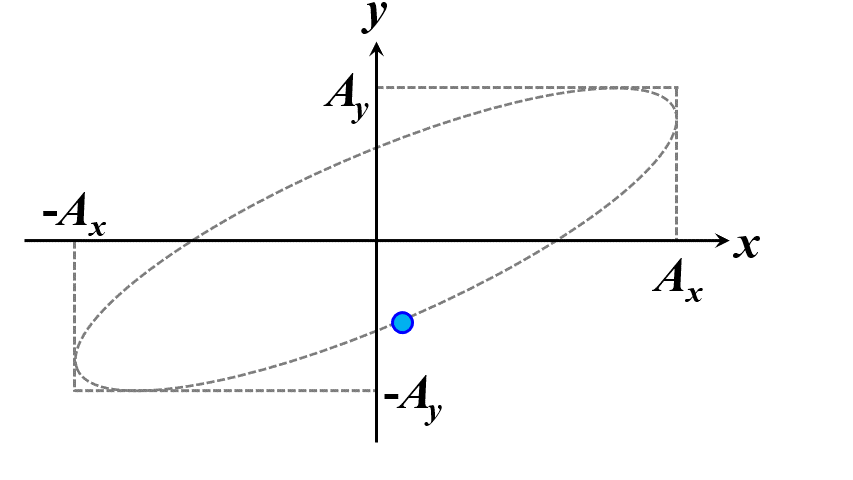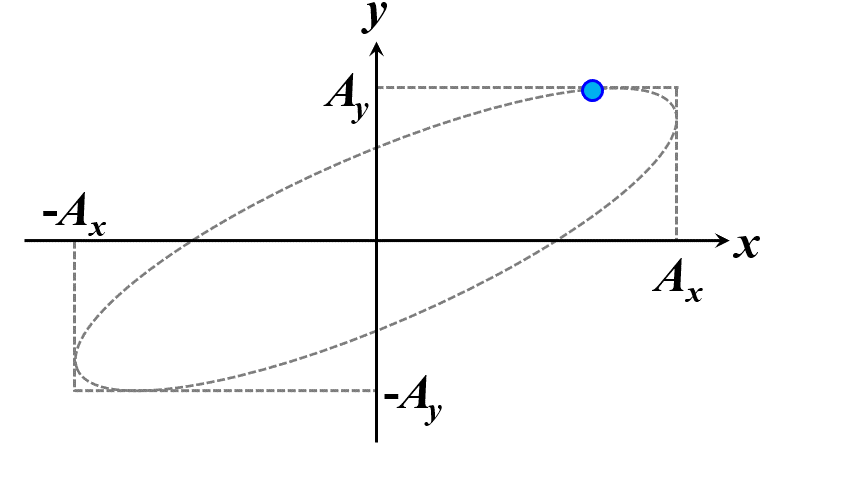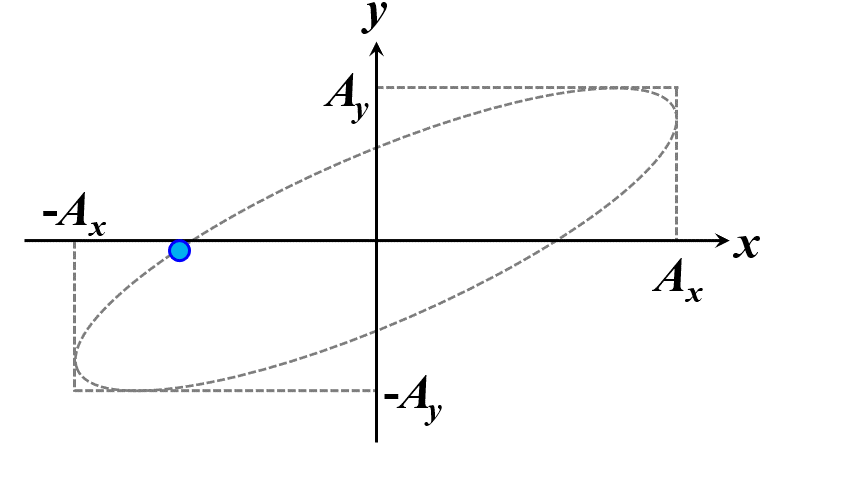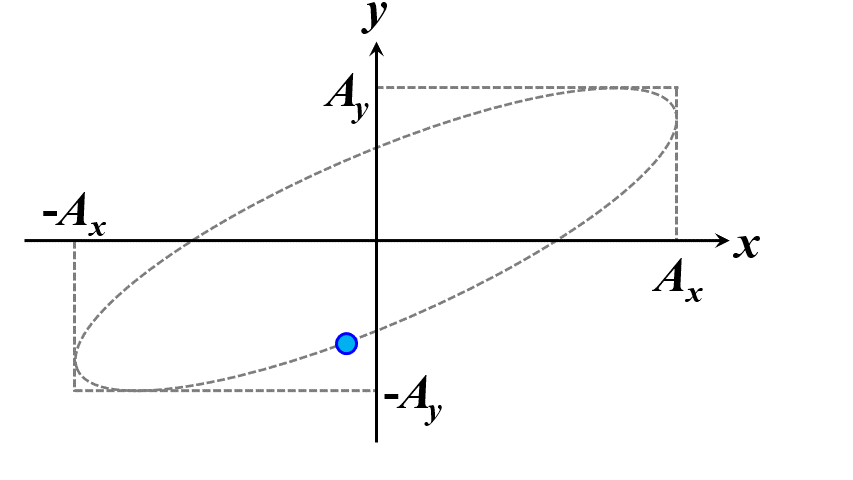 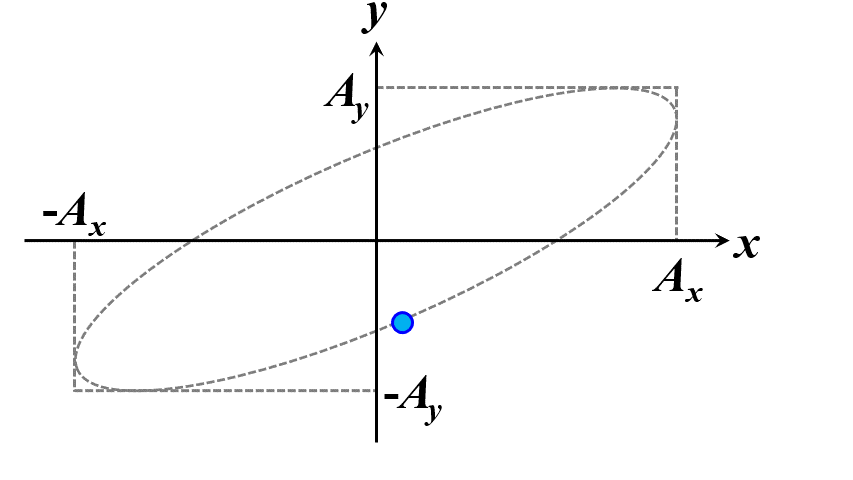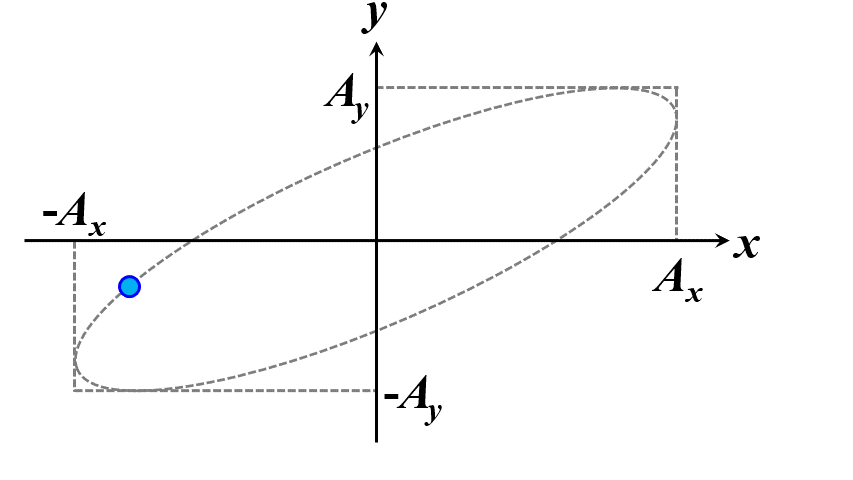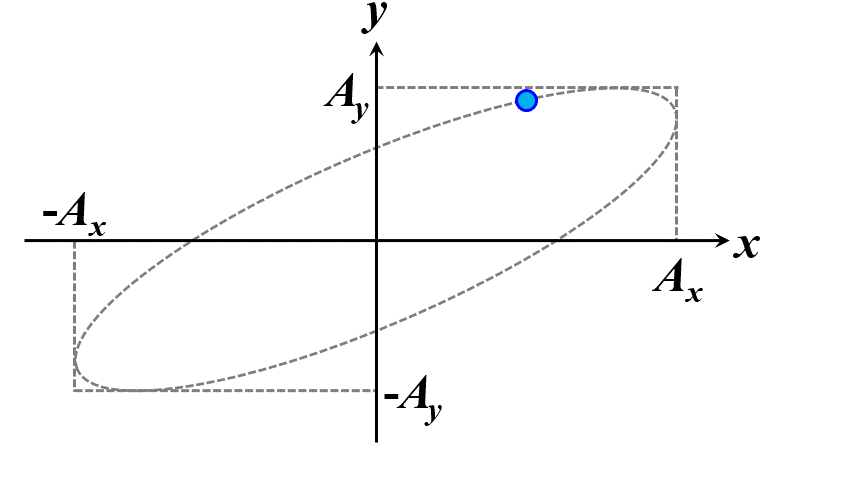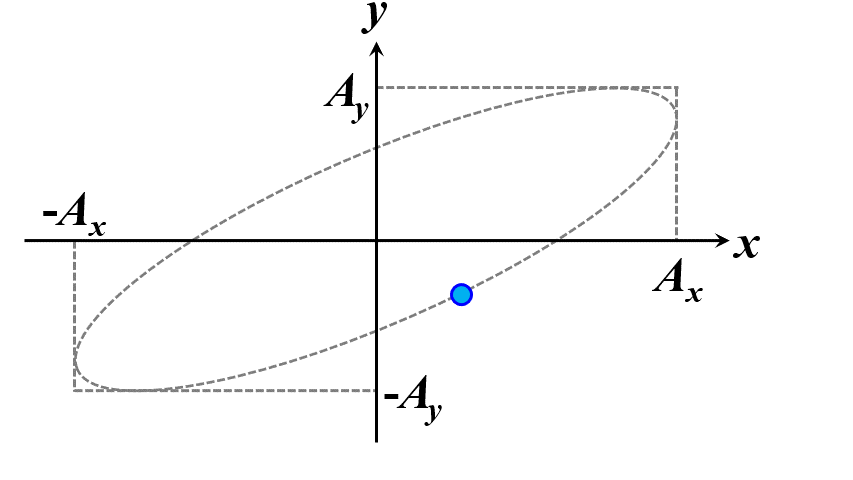 図2.1.4(a) 楕円偏光(左:\(-\cfrac{\pi}{2}<\delta<0\)、右:\(0<\delta<\cfrac{\pi}{2}\)) 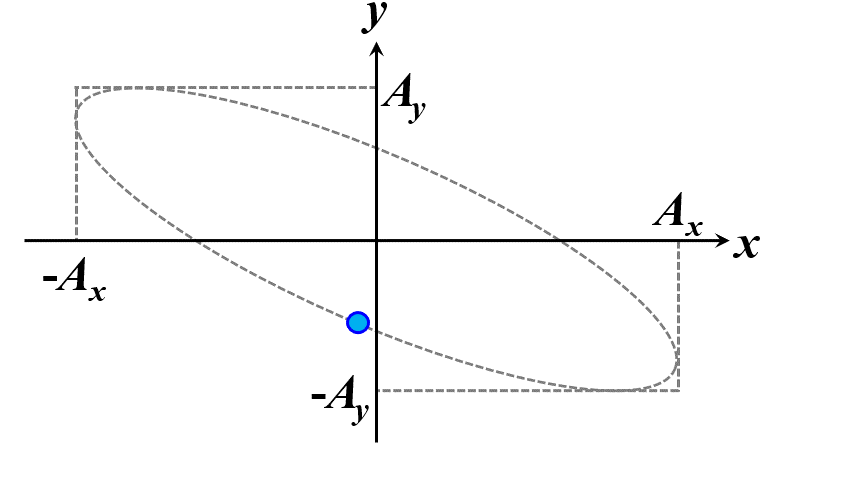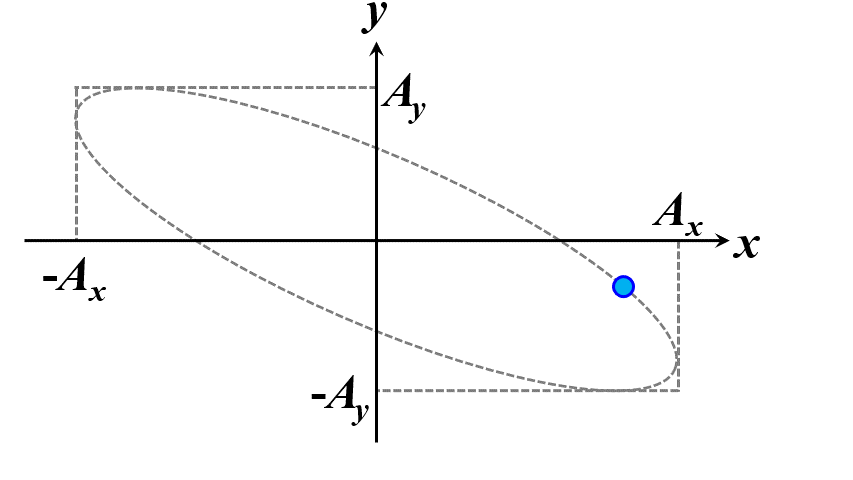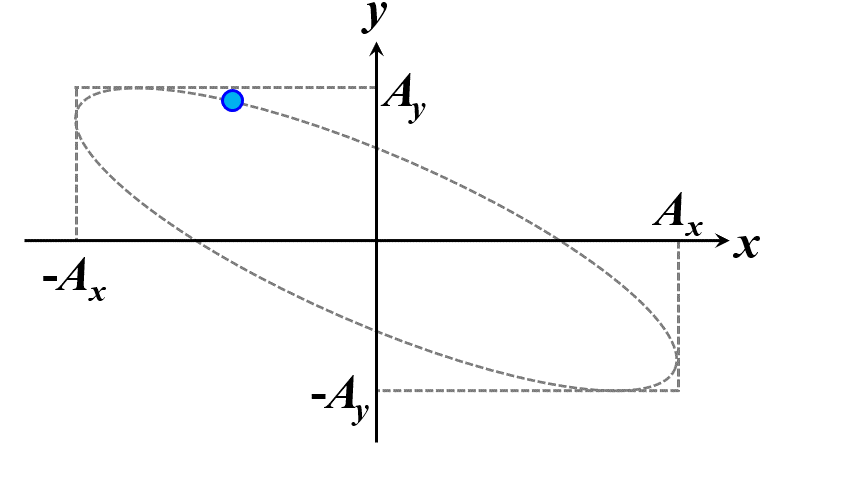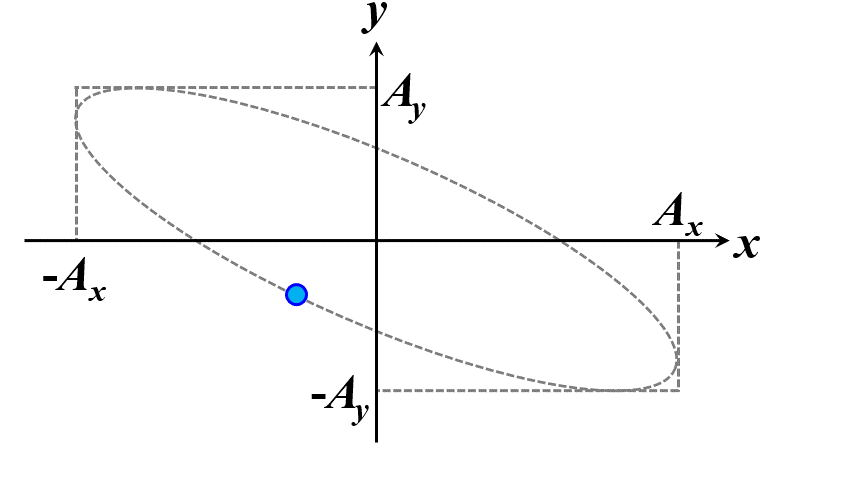 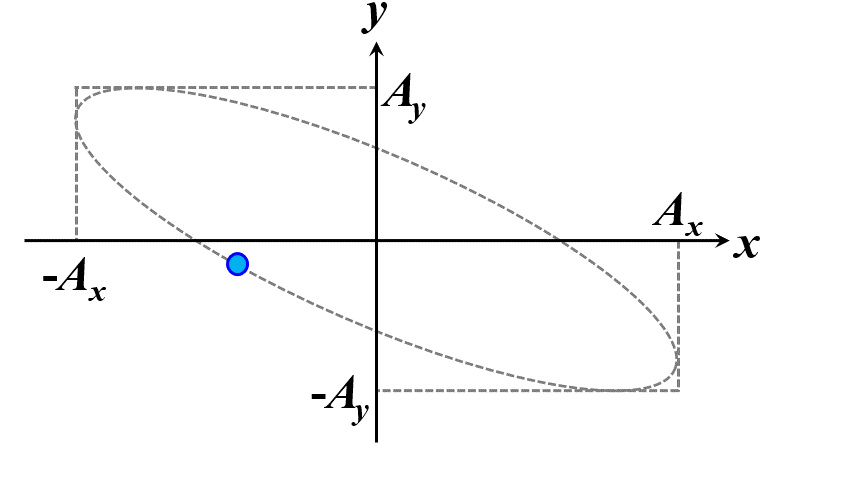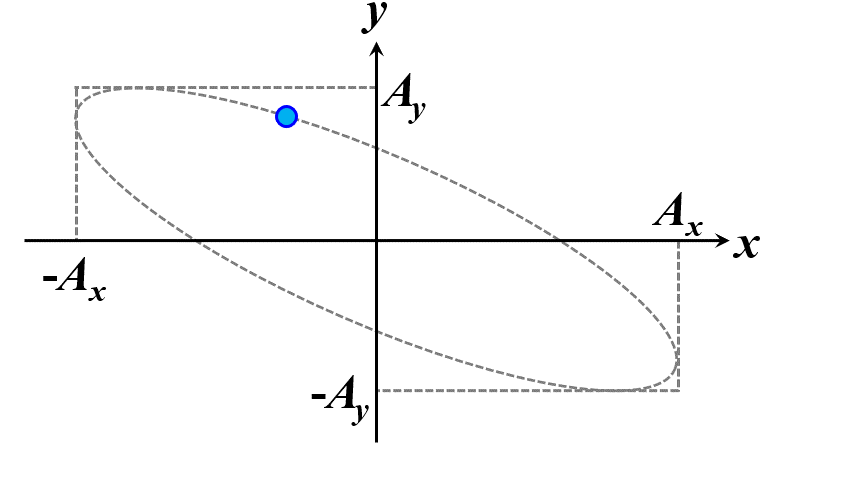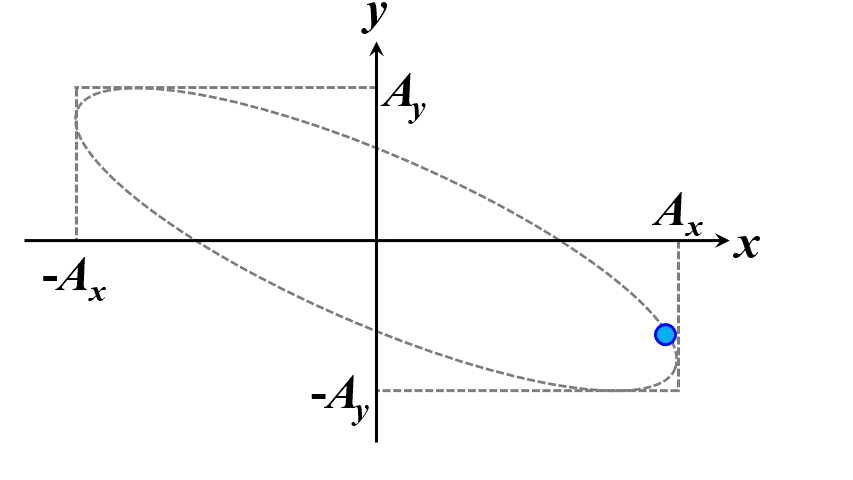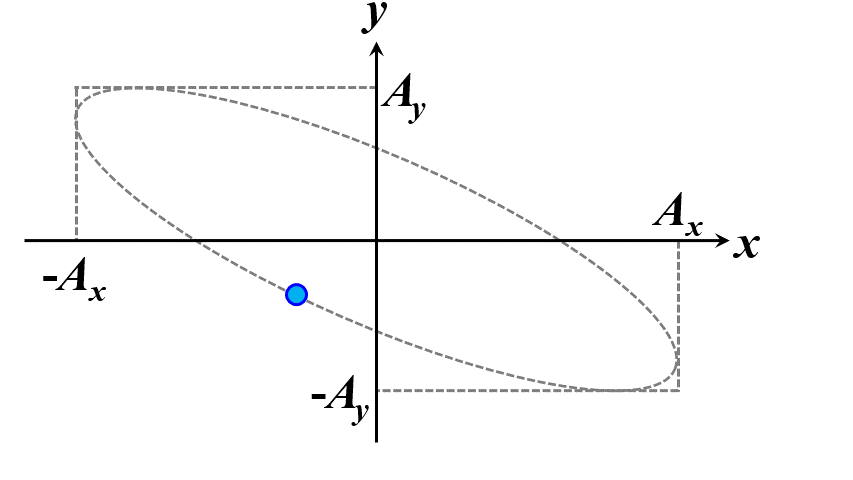 図2.1.4(b) 楕円偏光(左:\(-\pi<\delta<-\cfrac{\pi}{2}\)、右:\(\cfrac{\pi}{2}<\delta<\pi\)) 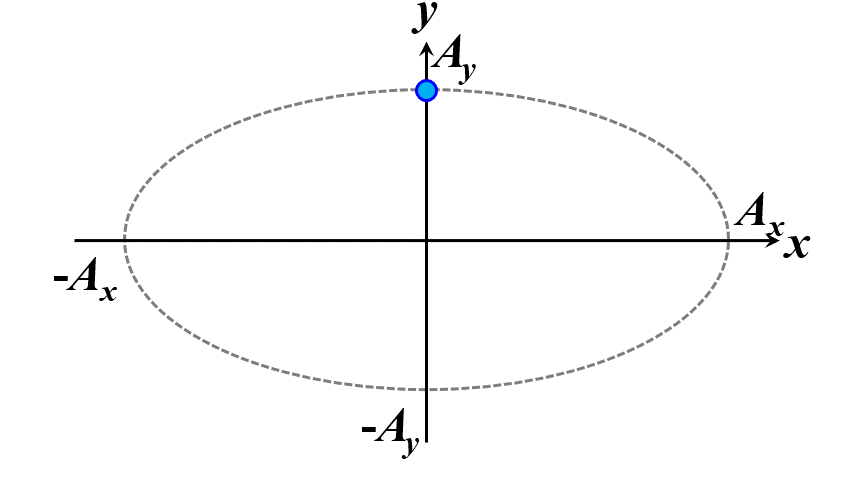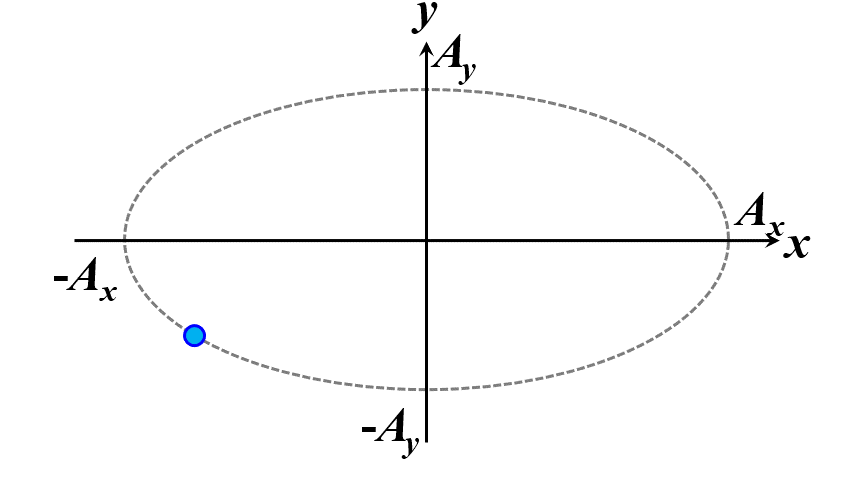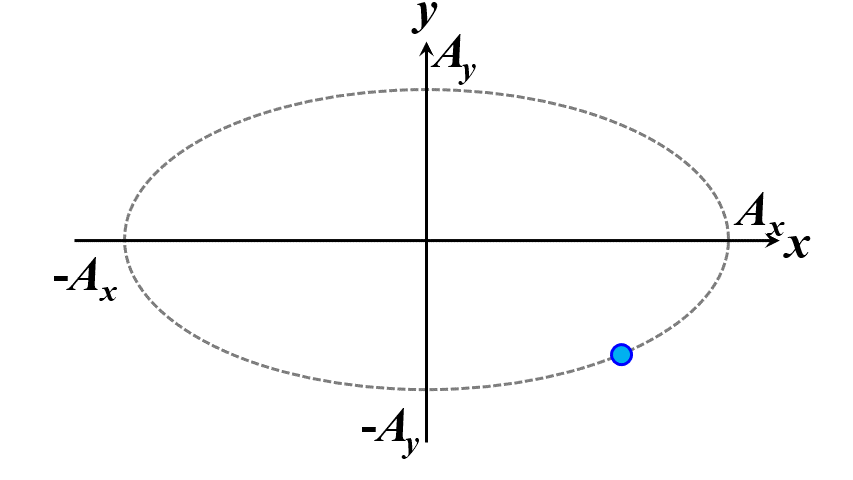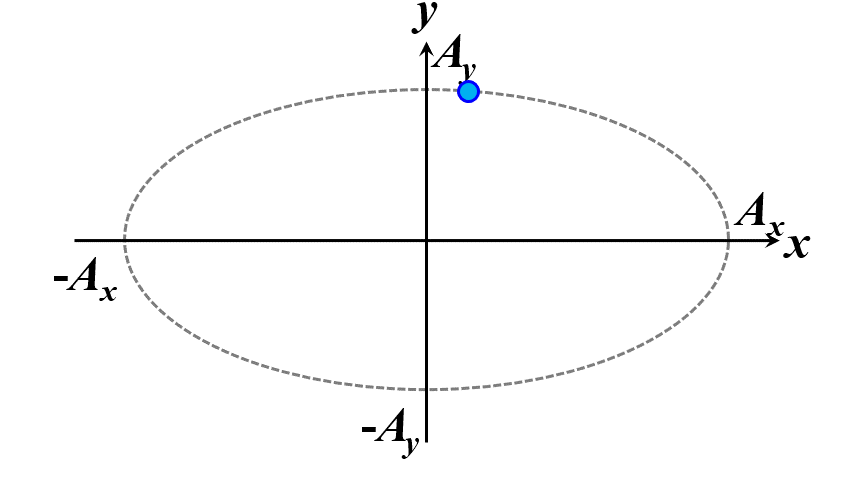 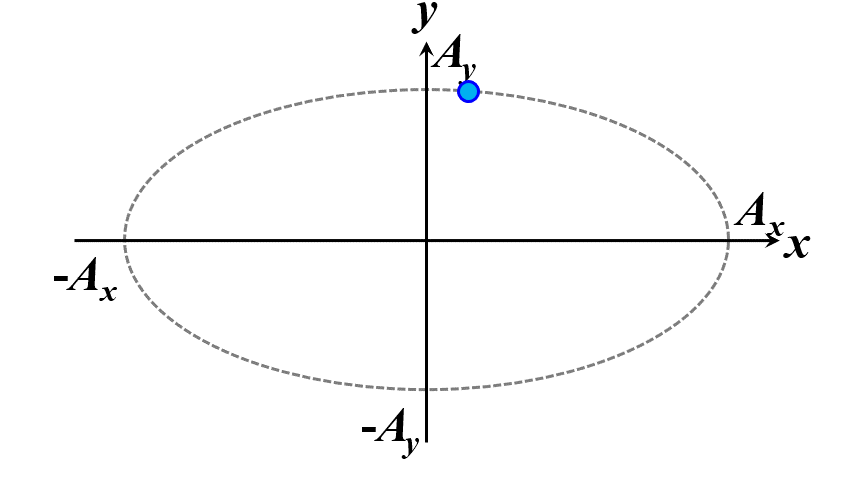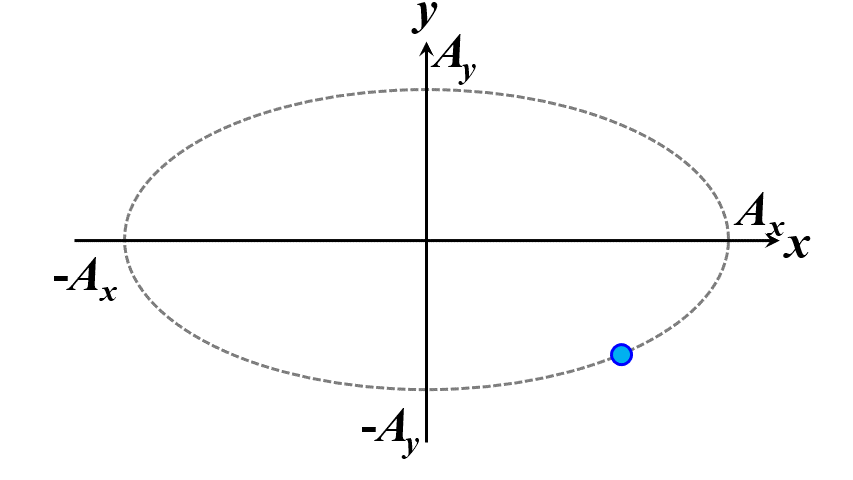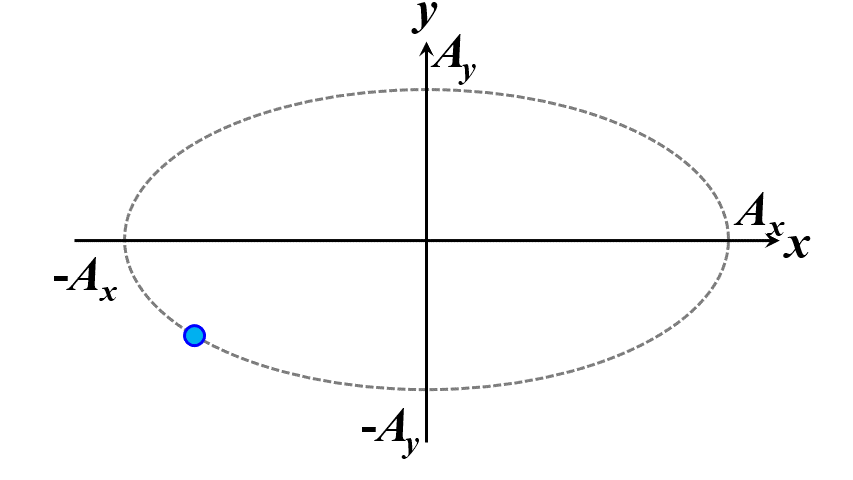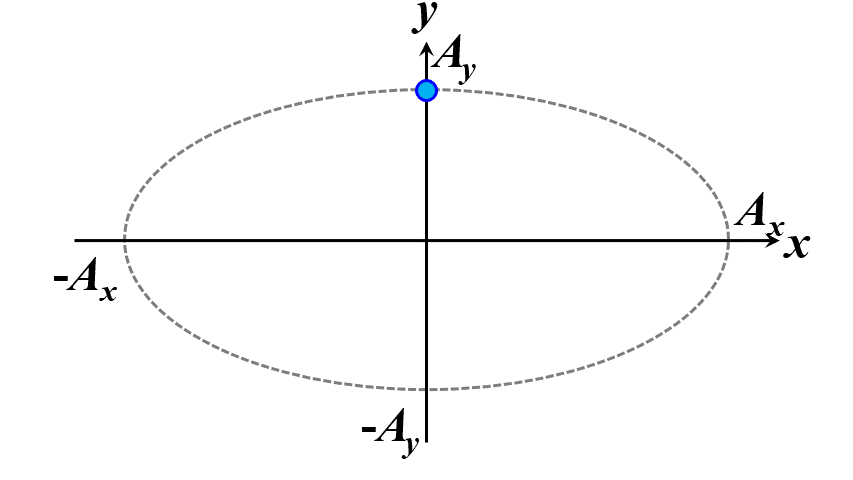 図2.1.4(c) 楕円偏光(左:\(\delta=-\cfrac{\pi}{2}\)、右:\(\delta=\cfrac{\pi}{2}\)) 図2.1.4において、左側の列は反時計まわりですので左まわり○○、右側の列は時計まわりですので右まわり○○と区別することがあります。注意しなければならないのは、左/右まわりの方向は、その光を観察している人の立場から定義されているということですね。 |
|
 | (c)で、\(A_x=A_y\)のとき、円に見えますね。 | |
 | はい。 \[ \phi_y - \phi _x = \delta = \pm \frac{ \pi }{ 2 }, \quad A_x = A_y \] の条件を満たすとき、円偏光と言います。 | |
 | いずれにしても、偏光がどうであれ、式2.1.3と式2.1.4の合成だってことか。 | |
 | その2つの波動は偏光で分類すると何になりますか?? | |
 | 直線偏光じゃないんですか?? | |
 |
ということで、偏光については次のようにまとめることができます。 ①偏光は、直交する2つの直線偏光に分解することができる ②それぞれの直線偏光の位相差\(\delta\)によって、偏光の種類が決まる ③一般には楕円偏光だが、条件によって直線偏光や円偏光になる |
|
 | 何となく、偏光についてはクリアできそうです。 | |
 | 1つハードルを越えたかもしれないですね。 |
| 前頁へ | 戻る | 次頁へ |