 | 1つ宿題が残ってましたね。 | |
 | どうして誘電体の比透磁率\(\mu_r\)は可視光領域で\(1\)になるのか、ですね。 | |
 |
これを理解するためには、媒質と電磁波の相互作用の由来を考える必要があります。原子の古典的なモデルは、図1.10.1のようなものです。
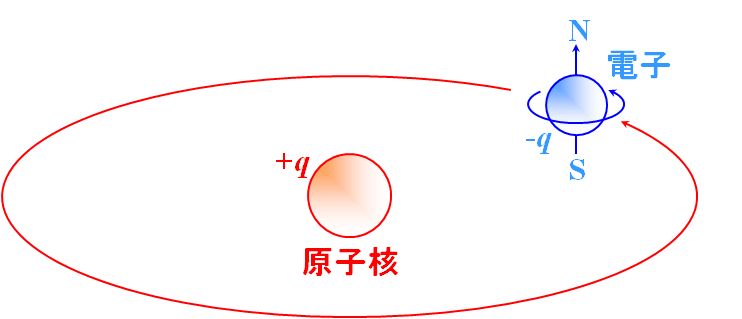 図1.10.1 原子モデル |
|
 | 中心に原子核があって、その周りを電子が公転しているっていうやつですね。 | |
 | それだけではなく、電子は自転もしています。尤も、自転という言い方は正確ではなくて、スピン角運動量を持っていると言った方がいいでしょう。 | |
 | 前回の講義だと、電子の電荷と外部電場の相互作用で誘電分極が生じるという話でしたね。 | |
 | そうです。つまり、誘電率の起源は、電磁波の電場成分と電荷との相互作用と考えられます。一方、電子のスピン角運動量は磁気モーメントを生じるので―。 | |
 | 透磁率の起源は、電磁波の磁場成分とスピン角運動量との相互作用?? | |
 | そのとおりです。通常の誘電体において電子のスピン角運動量は、周波数に換算して10GHz~100GHz程度になります。可視光の周波数はいくつくらいですか?? | |
 |
可視光の波長は凡そ400~800nmだから、式1.1.14を使って、 \(\nu\) = 3×108 m/s ÷ 400~800 nm = 375~750 THz ですね。 |
|
 | つまり、光の周波数はスピン角運動量よりも桁違いに高周波であることが分かります。ですから、外部磁場の周波数に追随できず、相互作用の起こりようがないのです。 | |
 | そうか。それで、どの誘電体でも\(\mu_r=1\)になるんですね。ということは、電磁波の周波数が小さくなれば、\(\mu_r\neq 1\)になる?? | |
 | なりますね。しかし、屈折率は式1.8.4のように、 \[ n = \frac{ c }{ v } = \sqrt{ \varepsilon_r \mu_r } \tag{1.8.4} \] 比誘電率と比透磁率の積で決定されるのに、こういう物理学的な制約で比透磁率の因子が無意味になるのは面白くありません。 | |
 | 私は別にそうは思いませんけど。 | |
 | 物理学者というのは、こういう制約に歯向かうものです。 | |
 | やれやれ…。 | |
 |
それどころか、\(\varepsilon_r<0\)、\(\mu_r<0\)という自然界には存在しないだろう、と考えられている媒質について検討する人たちが登場するのです。最初に、その検討に着手(論文)したのはVeselagoでした。
 Victor Georgievich Veselago(1929~2018) |
|
 | ないものについて検討してもしょうがないような気がしますけど。 | |
 |
しかし、1999年になって、Pendryという物理学者が、自然界に存在しないなら人工で作ればいいという提案をします(論文)。この世にない媒質を、この世にある材料で人工的に作るという意味でメタマテリアルと言います。
 Sir John Brian Pendry(1943~) |
|
 | メタって、メタ認知のメタですか?? | |
 | そうですね。 | |
 | 提案するのはいいけど、それで何か嬉しいことがあるんですか?? | |
 | \(\varepsilon_r<0\)、\(\mu_r<0\)ということは、屈折率が負になるということです。これまでの光学の常識がひっくり返ります。 | |
 | ひっくり返されると話がややこしくなるから、できればそっとしておいてほしいけどな。 | |
 | まぁ、どういう世界になり得るかというくらいは見ておきましょう(図1.10.2)。例えば、空気中(=媒質1)から水中(=媒質2)に向けて光が\(45^{\circ}\)で入射したとしましょう。屈折角はいくつになりますか?? | |
 |
え~と、水の屈折率は\(1.333\)だから、 \(\theta_2=\sin^{-1}(\sin 45^{\circ}/1.333)\fallingdotseq 32^{\circ}\) ですね(a)。 |
|
 | では、\(n=-1.333\)だったら?? | |
 |
その場合は、 \(\theta_2=\sin^{-1}(-\sin 45^{\circ}/1.333)\fallingdotseq -32^{\circ}\) かな(b)。 |
|
 |
つまり、このような光路になります。
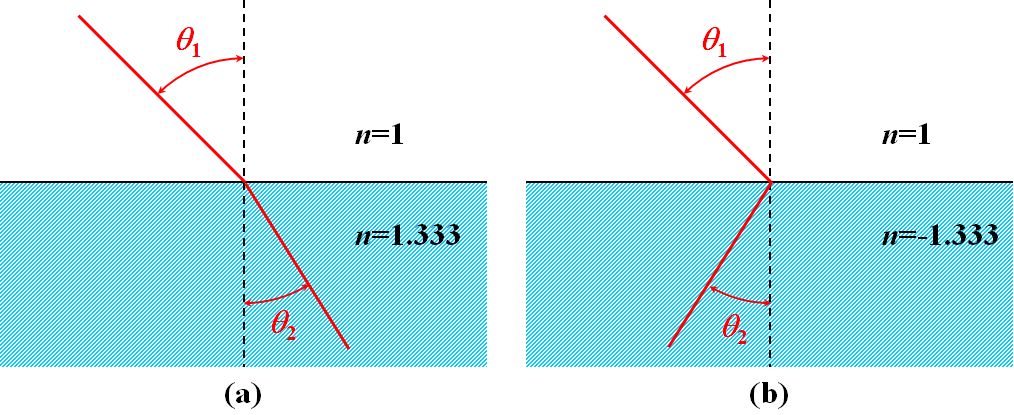 図1.10.2 Snellの法則 |
|
 | 何か、(b)は馴染みがないから気持ち悪いですね。 | |
 |
しかし、(b)のような光路をとることから、こんなレンズを作ることが可能になります。
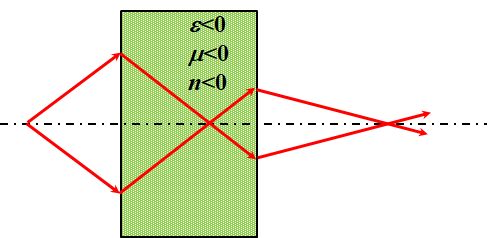 図1.10.3 スーパー・レンズ |
|
 | 入射側も出射側も平面のレンズですね。まぁ、薄型化には効果がありそうですけど。 | |
 | そうですね。メリットの1つとして挙げられると思います。それよりも、このレンズは別名スーパー・レンズとも呼ばれており、理論的には無限小の分解能を持つレンズ(論文)なんですよ。 | |
 | え??そうなんですか?? | |
 | 少なくとも、一般的なレンズの分解能を破ることはできます。すべての形状が無数の三角関数の足し合わせで表現できるというのは知ってますか?? | |
 | Fourier級数でしたっけ?? | |
 | はい。分解されたすべての三角関数の情報が余すことなく光に乗って伝搬されれば、それは無限小の分解能であると言うことができます。しかし、残念ながらすべての情報を伝搬させることはできません。 | |
 | なぜですか?? | |
 | 局在波と言って、その場に留まる頑固な波数成分の情報が存在するからです。 | |
 | 何と!! | |
 | この情報は、その場から離れると急速に消えてなくなってしまうため、伝搬された情報はその分だけ欠落していることになります。実は、これが分解能を決定しているんですよ。光の波数よりも大きな波数成分の情報が、局在波となります。 | |
 | 局在波の情報を伝搬させる工夫があればいいんですね?? | |
 | その工夫がスーパー・レンズです。もちろん、オリジナルの情報にう~んとレンズを近づける必要がありますが、局在波が減衰しきる前にキャッチしてやれば、負の屈折率の威力でその情報を増幅させることができるのです。だから、すべての情報を伝搬でき、ほぼ無限小の分解能が実現できます。 | |
 | う~ん。でも、実用的ではなさそうですね。 | |
 | あまり驚きませんか?? | |
 | 驚かないです。 | |
 | では、この技術で透明人間になれるとしたらどうでしょう?? | |
 |
え~。それは凄いじゃないですか。Wellsの小説みたいに、飲んだら透明になっちゃう薬みたいなイメージ??
 Herbert George Wells(1866~1946) |
|
 | まったく違います。そもそも、自分の身体が透明になっても、嬉しいことはないですよ。 | |
 | え??そんなことないですよ~。 | |
 | ありますよ。だって、透明人間には何も見えないですから。 | |
 | ん??どういうこと?? | |
 |
透明になるというのは、物理学的に周囲の屈折率と一緒になるということです。例えば、ビーカーの中にガラスのコップを入れて、サラダ油を注いでいくとコップは見えなくなりますよね。
|
|
 | あ、本当だ。 | |
 | これは、ガラスのコップの屈折率とサラダ油の屈折率が同じであるために、境界面を光が認識できなくて生じている現象です。 | |
 | つまり、光はそのまま抜けて行っちゃう?? | |
 | はい。となると、透明人間の目に入った光は網膜上に結像することはありません。 | |
 | 目が見えないって、そういうことか。 | |
 | まったく旨味がないですね。 | |
 | じゃぁ、メタマテリアルで透明人間になる方法って?? | |
 | クローキングという方法ですね。つまり、透明マントです。 | |
 |
ハリー・ポッターみたいな??
|
|
 | そうです。 | |
 | え~、それでも凄いですよ~。 | |
 |
このクローキング技術は、2006年にデューク大学のDavid Smithが開発したもので、マイクロ波で実証(論文)されました。
 David Smith(1964~) その後、2010年には可視光でも可能であることが実験的に確認(論文)されています。これを開発したAndrea De Falcoは、この物質をメタフレックスと呼んでいるようですね。  Andrea De Falco(1986~) |
|
 | 負の屈折率だと、そういうことができるわけですね?? | |
 |
いえ。この場合は、屈折率を人工的に制御することで実現できます。要するに、マントの表面は空気と限りなく同じ屈折率とし、中に行くほど屈折率が小さくなるように設計すると、マントの中を光が伝搬して、包まれた物体の向こう側の景色が目に届くんですよ。
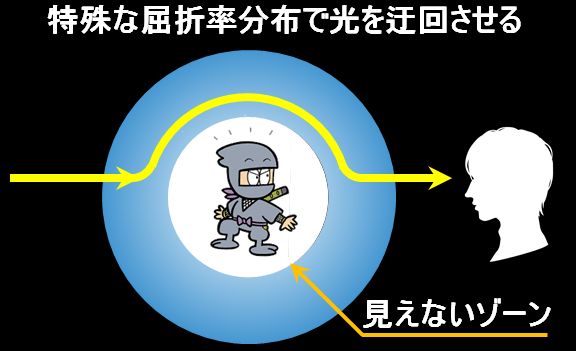 図1.10.4 クローキング |
|
 | なるほど~。 | |
 |
そして、2019年にはカナダの戦闘迷彩服開発企業であるハイパーステルス・バイオテクノロジー社が、それを実用化したというので話題になりました。量子ステルスと言うそうです。
|
|
 | 嘘!!これ、どうしたら手に入るんですか?? | |
 | 残念ながら、軍需用品なので手に入りません。 | |
 | え~、ほしいなぁ。 | |
 | どうせ邪なことしか考えてないんでしょうけど、この技術の真偽については、専門家も判断を控えているようです。 | |
 | ってことは、ガセネタってこともあり得る?? | |
 |
あり得ますね。何しろ、映像に関するトリック技術も格段に進んでますから。クロマキー合成の可能性は高いですよ。
|
|
 | な~んだ、残念。ところで、負の屈折率は、どうやって作っているんですか?? | |
 |
図1.10.5のメタマテリアルは初期のタイプですが、こういう構造体で負の屈折率を実現します。
 図1.10.5 メタマテリアル |
|
 | 棒みたいのと、視力検査のLandolt環みたいのがいっぱい見えますね。 | |
 | 棒みたいのは金属ワイヤ、Landolt環みたいのは分割リング共振器です。金属ワイヤが人工的に誘電率を制御する因子、分割リング共振器が人工的に透磁率を制御する因子になります。 |
~負の誘電率の導出~
 | こんな金属ワイヤで誘電率を制御できるんですか?? | |
 |
できますよ(論文)。まず、比誘電率\(\varepsilon_r\)が式1.9.7で表されることを思い出してほしいんですが、
\[
\varepsilon_r = 1 - \frac{ N q^2 }{ m_{\rm e} \varepsilon_0 } \frac{ 1 }{ \omega^2 - {\omega_0}^2 } \tag{1.9.7}
\]
図1.10.5の構造体の場合、復元力は期待できないので固有振動数\(\omega_0=0\)となります。また、図1.10.5の構造体を図1.10.1のような原子モデルと等価なものに置き換えたとして、電荷\(q\)の「電子もどき」を定義します。この質量を\(m_{\rm eff}\)としましょう。更に、金属ワイヤは半径\(r\)、長さ\(l\)の円柱とし、それが間隔\(a\)で配列されているとします。
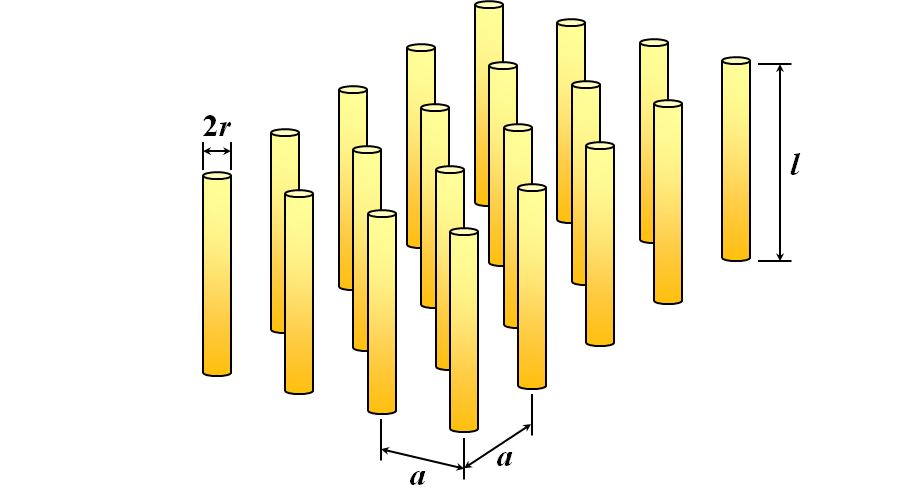 図1.10.6 金属ワイヤのメタマテリアル このとき、単位体積あたりの「電子もどき」の数\(N_{\rm eff}\)はどう書けますか?? |
|
 | \(a\times a\)という正方形の中に、\(\pi r^2\)という金属ワイヤが1本しかないから、金属ワイヤの電子の密度を\(n_{\rm e}\)として、 \[ N_{\rm eff} = n_{\rm e} \frac{ \pi r^2 }{ a^2 } \] かな。 | |
 | 従って、式1.9.7は、 \[ \varepsilon _{ r } = 1 - \frac{ N_{\rm eff} q^2 }{ m_{\rm eff} \varepsilon_0 } \frac{ 1 }{ \omega^2 } = 1 - n_{\rm e} \frac{ \pi r^2 }{ a^2 } \frac{ q^2 }{ m_{\rm eff} \varepsilon_0 } \frac{ 1 }{ \omega^2 } \tag{1.10.1} \] と修正されます。ちなみに、式1.9.1は式1.10.2のような運動方程式に修正されます(\(v\)は「電子もどき」の速度)。 \[ m_{\rm eff} \frac{ dv }{ dt } = q E \tag{1.10.2} \] 一方で、少し見方を変えると、外部電場の影響によって金属ワイヤに電流\(I\)が生じ、このとき隣接する金属ワイヤどうしは自己誘導によって誘導起電力\(e_{\rm i}\)を発生するので、次のような回路方程式が成立します(\(L\)は自己インダクタンス)。 \[ L \frac{ d I }{ dt } = e_{\rm i} = E l \tag{1.10.3} \] | |
 | 教授。ちょっと高校の参考書をとってきます…。 | |
 | 電気回路を復習してください。さて、式1.10.2と式1.10.3をアナロジーと捉えると、\(m_{\rm eff}\)の満たすべき形が分かりませんか?? | |
 | う~ん。こうかな?? \[ \frac{ m_{\rm eff} v }{ q } = \frac{ LI }{ l } \quad \Leftrightarrow \quad m_{\rm eff} = \frac{ LI }{ vl } q \tag{1.10.4} \] | |
 |
では、自己インダクタンス\(L\)を求めてみましょう。1本の金属ワイヤから生じる磁束密度\(B\)は、Biot-Savartの法則から、
\[
B = \mu_0 \frac{ I }{ 2 \pi R }
\]
です(\(R\)は金属ワイヤの中心からの距離)。
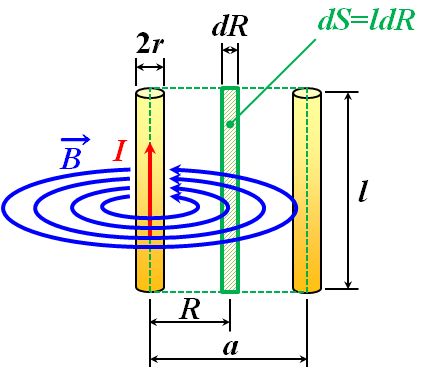 図1.10.7 磁束\(\Phi\)を求める そうすると、磁束\(\Phi\)は面要素\(dS\)を使って、 \[ \Phi = \int_{r}^{a} B dS = \int_{r}^{a} \mu_0 \frac{ I }{ 2 \pi R } l dR = \frac{ \mu_0 }{ 2 \pi }lI \big[ \ln R \big]_r^a = \frac{ \mu_0 }{ 2 \pi }lI \ln \left( \frac{a}{r} \right) \] となります。従って、 \[ L = \frac{ \Phi }{ I } = \frac{ \mu_0 }{ 2 \pi }l \ln \left( \frac{a}{r} \right) \tag{1.10.5} \] ですね。 |
|
 | 式1.10.5を式1.10.4に代入すると、 \[ m_{\rm eff} = \frac{ \mu_0 }{ 2 \pi } \frac{ I }{ v } q \ln \left( \frac{a}{r} \right) \tag{1.10.6} \] | |
 | 電流の定義は、ある面を1秒間に通過する電荷量ですから、 \[ I = \pi r^2 v n_{\rm e} q \tag{1.10.7} \] と書けます。 | |
 | そうすると、今度は式1.10.7を式1.10.6に代入か…。 \[ m_{\rm eff} = \frac{ \mu_0 }{ 2 } q^2 r^2 n_{\rm e} \ln \left( \frac{a}{r} \right) \tag{1.10.8} \] | |
 | というわけで、式1.10.1は次のようになります。 \[ \varepsilon _{ r } = 1 - \frac{ 2 \pi }{ \varepsilon_0 \mu_0 a^2 \ln \left( \cfrac{a}{r} \right) } \frac{ 1 }{ \omega^2 } = 1 - \frac{ 2 \pi c^2 }{ a^2 \ln \left( \cfrac{a}{r} \right) } \frac{ 1 }{ \omega^2 } \tag{1.10.9} \] 最後は、式1.4.8を使いました。 | |
 | てことは、 \[ \frac{ 2 \pi c^2 }{ a^2 \ln \left( \cfrac{a}{r} \right) } > \omega^2 \] というように金属ワイヤを設計すれば比誘電率は負になるわけですね。 |
~負の透磁率の導出~
 | では、次に分割リング共振器の振る舞いを見てみましょう。誘電率の起源は電子のスピン角運動量でしたが、これに代わる「スピンもどき」を考える必要があります。しかし、そのヒントはすでに手に入れているんです。 | |
 | ん??そうですか?? | |
 | 何もない空間に、巨大な磁石が存在してますよね?? | |
 | あ。地磁気のダイナモ理論。 | |
 |
そうです。ダイナモ理論では外殻の液体金属が地磁気の起源でしたが、円電流を作ってやれば、そのリングの中に磁気モーメント\(m\)が発生します。
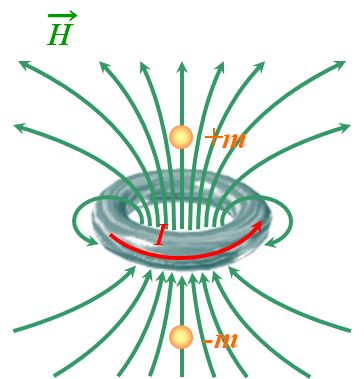 図1.10.8 円電流 |
|
 | 磁気モーメント\(m\)は、円電流のケースだと、どう書けるんですか?? | |
 | リングの内側の面積を\(S\)とすると、 \[ m = \mu_0 IS \tag{1.10.10} \] のように書けます(\(I\)はリングを流れる電流)。 | |
 | この電流\(I\)は、どうやって発生させるんですか?? | |
 | 外部磁場がかかるとFaradayの法則によって発生するでしょう?? | |
 | あ、そうか。 | |
 |
Pendryの工夫は、このリングに切れ目を入れたことですね。
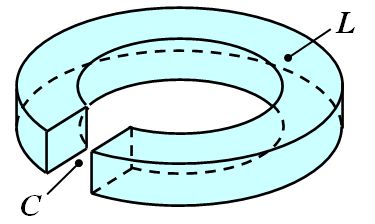 図1.10.9 分割リング共振器 |
|
 | そうすると、何かいいことがあるんですか?? | |
 | 切れ目がコンデンサーの役割を果たすのです。リングそのものはインダクタンスを持っているので、回路的にはコンデンサーとインダクタが並列に接続された共振回路を構成することになるんですね。コンデンサーの容量を\(C\)、インダクタンスを\(L\)とすると、その共振周波数\(\omega_{\rm LC}\)は、 \[ {\omega_{\rm LC}}^2 = \frac{ 1 }{ LC } \tag{1.10.11} \] のように書けます。 | |
 | これが、式1.9.1で出てきた共振周波数\(\omega_0\)に相当するわけですね?? | |
 | そうです。そして、磁束\(\Phi\)としたとき、図1.10.9の分割リング共振器には式1.10.12のような回路方程式が成立します。 \[ L \frac{ dI }{ dt } + \frac{ 1 }{ C } \int I dt = - \frac{ d \Phi }{ dt } \tag{1.10.12} \] | |
 | やっぱり電気回路なのか…。 | |
 | 式1.10.12は微分と積分が入り混じっているので、更に時間で微分しておきましょう。 \[ L \frac{ d^2 I }{ dt^2 } + \frac{ I }{ C } = - \frac{ d^2 \Phi }{ dt^2 } \tag{1.10.13} \] 磁束\(\Phi\)は、このケースだと、 \[ \Phi = \mu_0 H S \tag{1.10.14} \] です。 | |
 | 誘電率のときと同じように、 \[ H \big( \vec{\mathstrut r}, t \big) = H \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } \tag{1.10.15} \] \[ I \left( t \right) = I_0 \mathrm{e}^{-i \omega t } \tag{1.10.16} \] って置けばいいですか?? | |
 | OKです。 | |
 | そうすると…。 \[ \begin{align*} &- \omega^2 L I_0 \mathrm{e} ^{-i \omega t } + \frac{ I_0 \mathrm{e} ^{-i \omega t } }{ C } = - \frac{ d^2 \Phi }{ dt^2 } = - \mu_0 S \frac{ d^2 H }{ dt^2 } = \mu_0 S \omega^2 H \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } \\ &\Leftrightarrow \quad - \omega^2 L I_0 + \frac{ I_0 }{ C } = \mu_0 S \omega^2 H \big( \vec{\mathstrut r} \big) \\ &\Leftrightarrow \quad \left( \frac{ 1 }{ LC } - \omega^2 \right) I_0 = \frac{ \mu_0 S }{ L } \omega^2 H \big( \vec{\mathstrut r} \big) \tag{1.10.17} \end{align*} \] | |
 |
図1.10.5を見ると、分割リング共振器がいっぱい配列されてますよね。そこで、分割リング共振器は1つの平面内で間隔\(a\)で配列されており、その平面が間隔\(b\)で積み重なっているとしましょう。
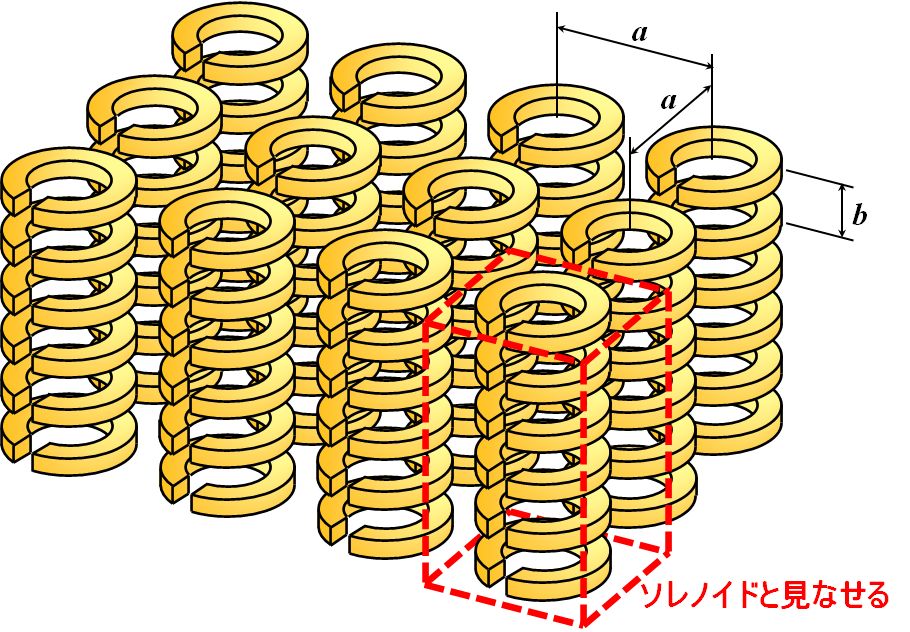 図1.10.10 分割リング共振器のメタマテリアル このとき、\(b\)に沿った方向で考えると、分割リング共振器の連なりは「長さ\(b\)に1巻きのソレノイド」と捉えることができます。つまり、そのようなソレノイドが間隔\(a\)で林立していると見なせます。従って、分割リング共振器1個あたりのインダクタンス\(L\)は次のように求まります。 \[ L = \frac{ \mu_0 S }{ b } \tag{1.10.18} \] また、式1.10.11を考慮すると―。 |
|
 | 式1.10.17は、 \[ \left( {\omega_{\rm LC}}^2 - \omega^2 \right) I_0 = b \omega^2 H \big( \vec{\mathstrut r} \big) \quad \Leftrightarrow \quad I_0 = \frac{ \omega^2 }{ {\omega_{\rm LC}}^2 - \omega^2 } b H \big( \vec{\mathstrut r} \big) \tag{1.10.19} \] ですね。 | |
 | さて、電束密度、電場、誘電分極の間には、式1.9.5から次のような関係が成立するわけですが、 \[ D = \varepsilon E = \varepsilon_0 E + P \] 磁束密度、磁場の間にも、誘電分極に相当する磁化分極\(M\)を定義することができます。 \[ B = \mu H = \mu_0 H + M \tag{1.10.20} \] | |
 | 電気と磁気のアナロジーですね。 | |
 | そして、磁化分極\(M\)は磁化率を\(\chi_{\rm m}\)と置くと、磁場の強くない範囲において、 \[ M = \chi_{\rm m } \mu_0 H \tag{1.10.21} \] と書けるので、式1.10.20は次のように変形できます。 \[ \mu H = \mu_0 H + \chi_{\rm m } \mu_0 H = \mu_0 \left( 1 + \chi_{\rm m} \right) H \tag{1.10.22} \] | |
 | そうすると、比透磁率は \[ \mu_r = 1 + \chi_{\rm m} \tag{1.10.23} \] ですか…。 | |
 | また、微視的には、磁気モーメント\(m\)を持つ粒子が集合して磁化分極\(M\)を作っていると考えられますので、固体の体積を\(V\)、その固体に含まれる粒子の数を\(n_{\rm m}\)とすると、 \[ M = \frac{ n_{\rm m }}{ V } m \tag{1.10.24} \] と定義されます。図1.10.10のようなメタマテリアルだと、粒子=分割リング共振器ですね。 | |
 | 教授。体積\(V\)は、 \[ V = a^2 b n_{\rm m } \tag{1.10.25} \] ってなりませんか?? | |
 | そうですね。式1.10.24は、 \[ M = \frac{ n_{\rm m }}{ V } m = \frac{ n_{\rm m }}{ a^2 b n_{\rm m } } m = \frac{ 1 }{ a^2 b } m \tag{1.10.26} \] としておきましょう。 | |
 | う~ん。式がいっぱい出てきたなぁ。そうすると、式1.10.26に式1.10.10と式1.10.21を代入して、 \[ \chi_{\rm m } \mu_0 H = \mu_0 \frac{ IS }{ a^2 b } \quad \Leftrightarrow \quad \chi_{\rm m } H = \frac{ IS }{ a^2 b } \tag{1.10.27} \] で、これに式1.10.19を代入か…。 \[ \begin{align*} &\chi_{\rm m } H \big( \vec{\mathstrut r} \big) = \frac{ S }{ a^2 b } \frac{ \omega^2 }{ {\omega_{\rm LC}}^2 - \omega^2 } b H \big( \vec{\mathstrut r} \big) =\frac{ S }{ a^2 } \frac{ \omega^2 }{ {\omega_{\rm LC}}^2 - \omega^2 } H \big( \vec{\mathstrut r} \big) \\ &\Leftrightarrow \quad \chi_{\rm m } = \frac{ S }{ a^2 } \frac{ \omega^2 }{ {\omega_{\rm LC}}^2 - \omega^2 } \tag{1.10.28} \end{align*} \] | |
 | \(\cfrac{S}{a^2}\)は、分割リング共振器の面積占有率を意味しますが、それをフィリング・ファクター\(F\)と定義すると、比透磁率は、 \[ \mu_r = 1 + \frac{ F \omega^2 }{ {\omega_{\rm LC}}^2 - \omega^2 } \tag{1.10.29} \] と求まるわけです。 | |
 | てことは、 \[ \frac{ {\omega_{\rm LC}}^2 }{ 1 - F } < \omega^2 \] というようにリング共振器を設計すれば比透磁率は負になるわけですね。 | |
 | そういうことになります。ここでは、1重リングで計算しましたが、図1.10.5のような2重リングの場合も、等価回路方程式を立てて計算すれば、同じように議論することができます。 | |
 | メタマテリアルの大きさって、光を騙す程度でないといけないですよね?? | |
 | そうです。つまり、波長よりも小さいサイズの構造体が求められます。だからこそ最初は、構造体が比較的扱いやすいマイクロ波で実証されたんですよ。それと同様の理由で、テラヘルツ波でのメタマテリアル研究もやられてますね。 | |
 | 可視光だと数nmレベルか…。 | |
 | その程度の構造体を作製すること自体は、2光子還元法などで可能なんですが、それを巨視的なレベルで配列する方法が確立できてません。それと、可視光すべてに対してメタマテリアルの効果を発揮させるのも難しいでしょう。だから、量子ステルスができたというさっきのニュースは、俄かには信じがたいということなんです。 | |
 | この技術は音波でも可能?? | |
 | その場合は音響メタマテリアルと呼ばれます。これは、すでに実用化されていて、2020年に日産自動車㈱がロード・ノイズを脅威的に削減したというので話題になりましたね。 | |
 | こういう技術は、いろいろなところで使われていきそうですね。 | |
 | そうですね。 | |
 | ということは、クローキング技術も…。 | |
 | 実現は夢物語じゃないと思います。 |
| 前頁へ | 戻る | 次頁へ |