 |
白色光をプリズムに入射させると虹色に色分解するというのは知ってますか??
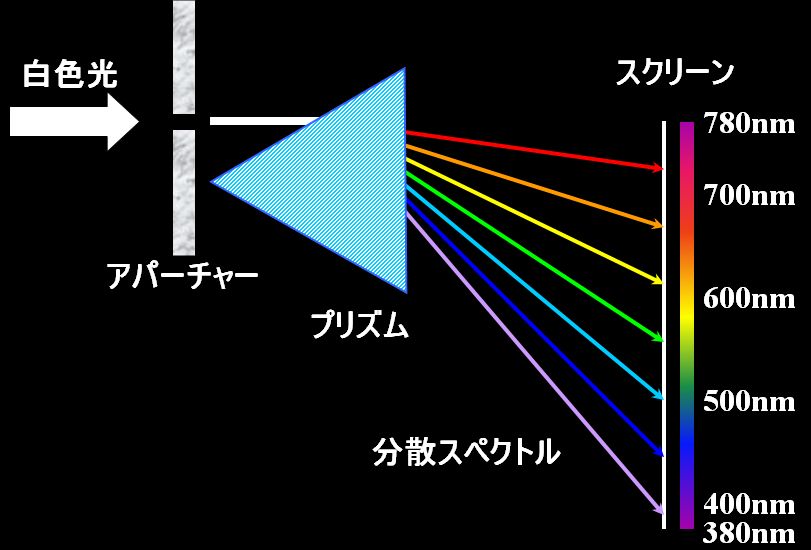 図1.9.1 分散 |
|
 | 分散ですね。 | |
 |
分散について詳細に議論をしたのは、かの有名なNewtonです。
 Sir Isaac Newton(1642~1727) |
|
 | 物理学の巨人ですね。 | |
 | そういうふうによく言われますけど、この人は何が凄いか分かります?? | |
 | ん??リンゴが落ちるのを見て万有引力を発見した、ってことでは?? | |
 | Newtonの凄さは、いろいろな切り口で説明できるとは思いますが、個人的には次のように考えています。それまでの物理学は、「ある時刻\(t\)において、物理量\(a\)がどのように表現できるか」という着想で考えられていました。つまり、\(a=f(t)\)ですね。 | |
 | 素直な発想だと思いますけど?? | |
 | はい。古代ギリシャ時代は、現代でも充分に通用する高度な思考が華々しく開花した時代でもありますが、やはり現代からすると、非常に素朴な発想に基づく考察も多く見られます。\(a=f(x)\)という単純な因果律は、その典型とも言えるものですね。しかし、Newtonはこの見方をきっぱりと否定します。 | |
 | ふむ。 | |
 | Newtonの考える物理学の本質とは、「\(t_1\)から\(t_2\)に時刻が変化したときに、物理量が\(a_1\)から\(a_2\)に変化した、その変化率にあり」というものです。 | |
 | 変化が重要ということですね。 | |
 | そうです。だから、それを表現する数学アイテムが必要となり、自力で微分・積分を構築していくのです。 | |
 | そうか。確か、Newtonがその分野の創始者でしたっけね。 | |
 | ですから、よく思い出してください。実際、物理学の基礎方程式と呼ばれるものは、1つの例外もなく微分方程式で表現されてませんか?? | |
 | ん~。Newton方程式、Maxwell方程式、Bernoulli方程式、Schrödinger方程式、Einstein方程式―。 | |
 | Navier-Stokes方程式、Heisenberg方程式、Klein-Gordon方程式、Dirac方程式…。 | |
 | 本当だ!! | |
 | そういうわけで、Newtonは死後、どんどん神格化されていくわけです。Newtonは『プリンキピア』という本の中で運動方程式を初めて論じているんですが…。読んだことあります?? | |
 | 当然、ないで~す。 | |
 | ま、そうでしょうね。現代において、必読書ではないですし、殆ど文章と図形で説明されているので、めちゃめちゃ分かりづらいですし。 | |
 | ん??文章と図形??方程式は出てこない?? | |
 |
出てきません。『プリンキピア』の内容を今の方程式の形に整えたのはEulerだと言われています。
 Leonhard Euler(1707~1783) |
|
 | Maxwell方程式のときもそうだったけど、未整備デビューっていうの、多いですね…。 | |
 | さて、幾何光学では、分散について「屈折率は物質固有の値ではなく、波長依存性があり、赤い光ほど屈折率が小さく、紫の光ほど屈折率が大きい」と説明されることが多いです。 | |
 | そうですね。よく、どっちの色で屈折率が小さいか忘れますけど…。 | |
 | ところが、Maxwell方程式から導かれた屈折率は、式1.8.4から分かるように誘電率と透磁率だけで決まる定数です。ここまでの議論で波長依存性は出てきてません。 | |
 | あ、確かに。てことは、Maxwell方程式が間違っている?? | |
 | そうではないです。実は、分散を議論するためには、もう1つモデルを持ってこないといけません。このモデルは厳密には量子論が必要になるんですが、近似的には古典電子論で充分です。 | |
 | そのモデルとは?? | |
 | Drude-Lorentzモデルと言います。 | |
 | Lorentz??Lorentz変換の?? | |
 |
そうです。Lorentzは誘電体のモデルを、Drudeは金属のモデル(論文)を構築しました。
 Paul Karl Ludwig Drude(1863~1906) Drudeは、その当時MaxwellやBoltzmannといった人たちによって提唱された気体分子運動論を金属の自由電子に適用して、電流と抵抗の発生メカニズムを理論的に解明した人です  Ludwig Eduard Boltzmann(1844~1906) |
|
 | Lorenztモデルを金属に拡張したイメージかな。 | |
 | そうですね。さて、均質・等方性・非吸収媒質中の電磁波の伝搬を議論したとき、誘電体は巨視的な電荷の移動は起こらない(\(\rho=0\))と説明しました。 | |
 | はい。 | |
 |
しかし、微視的にはそうではありません。外からの電場は正負の粒子に対して逆向きの力を及ぼすので、互いに反対方向に僅かながら変位します。これを誘電分極と言います。
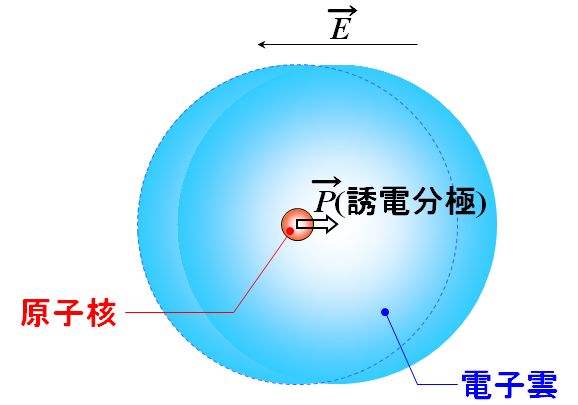 図1.9.2 誘電分極 |
|
 | 変位して、そのままバラバラにはならない?? | |
 | 正負の電荷を強く結んでいる電磁気的な力があるため、バラバラにはなりません。 | |
 | 電子雲ってありますけど?? | |
 | 電子は波動と粒子の2面性がありましたね。 | |
 | de Broglieの式でしたっけ。 | |
 | 電子を波と捉えたときに、その波が原子核を覆っているというイメージを模式的に描いたときに使われるテクニカル・タームが電子雲です。この様子をNewton方程式で記述すると次のようになります。 \[ m_{\rm e} \frac{ d^2 \vec{\mathstrut u} }{ dt^2 } = q \vec{\mathstrut E } - m_{\rm e } {\omega_0 }^2 \vec{\mathstrut u } \tag{1.9.1} \] | |
 | え~と、記号が…。\(m_e\)は電子の質量、\(\vec{\mathstrut u}\)は電子の位置、\(q\)は電子の電荷、\(\vec{\mathstrut E}\)は電場―。\(\omega_0\)?? | |
 | 式1.9.1の右辺の第2項は、単振動で出てくる復元力です。 | |
 | バネの振動で、元に戻そうとする力のこと?? | |
 | そうです。電場は式1.1.12のように周期的な関数(三角関数)で与えられるのが分かっているので、復元力も同じタイプの関数で表現できそうですよね。だから、その固有振動数(共振周波数)を\(\omega_0\)として、予め式1.9.1の中に組み込んでいるわけです。 | |
 | 原子核の運動に関する記述がないですけど?? | |
 | 原子核を構成している陽子は電子に比べて1,840倍も重いので、無視できますよ。 | |
 | なるほど。で、式1.9.1を解くわけですね?? | |
 | まず、式1.9.1の形から、時間成分だけが対象となることが分かるので、電場は次のように簡単に書いておきましょう。 \[ \vec{\mathstrut E} \big( \vec{\mathstrut r}, t \big) = E \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } \tag{1.9.2} \] | |
 | とすると、\(\vec{\mathstrut u}\)は、こんな感じ?? \[ \vec{\mathstrut u} \big( \vec{\mathstrut r}, t \big) = u \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } \tag{1.9.3} \] | |
 | では、式1.9.2と式1.9.3を式1.9.1に代入してください。 | |
 | ん~と。 \[ \begin{align*} &-m_{\rm e} \omega^2 u \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } = q E \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } - m_{\rm e} {\omega_0}^2 u \big( \vec{\mathstrut r} \big) \mathrm{e}^{-i \omega t } \\ &\Leftrightarrow \quad -m_{\rm e} \omega^2 u \big( \vec{\mathstrut r} \big) = q E \big( \vec{\mathstrut r} \big) - m_{\rm e} {\omega_0}^2 u \big( \vec{\mathstrut r} \big) \\ &\Leftrightarrow \quad m_{\rm e} \left( \omega^2 - {\omega_0}^2 \right) u \big( \vec{\mathstrut r} \big) = -q E \big( \vec{\mathstrut r} \big) \\ &\Leftrightarrow \quad u \big( \vec{\mathstrut r} \big) = \frac{ -q E \big( \vec{\mathstrut r} \big) }{ m_{\rm e} \left( \omega^2 - {\omega_0}^2 \right) } \tag{1.9.4} \end{align*} \] | |
 | 誘電分極\(\vec{\mathstrut P}\)は、電束密度\(\vec{\mathstrut D}\)を使って、次のように定義されます(比誘電率\(\varepsilon_r=\cfrac{\varepsilon}{\varepsilon_0}\))。 \[ \vec{\mathstrut P} = \vec{\mathstrut D} - \varepsilon_0 \vec{\mathstrut E} = \varepsilon \vec{\mathstrut E} - \varepsilon_0 \vec{\mathstrut E} = \varepsilon_r \varepsilon_0 \vec{\mathstrut E} - \varepsilon_0 \vec{\mathstrut E} = \varepsilon_0 \left( \varepsilon_r - 1 \right) \vec{\mathstrut E} \tag{1.9.5} \] また、単位体積あたりの誘電分極に寄与する電子の数を\(N\)とすると、誘電分極\(\vec{\mathstrut P}\)は、 \[ \vec{\mathstrut P} = N q \vec{\mathstrut u} \tag{1.9.6} \] というようにも表現できます。 | |
 | 式1.9.5と式1.9.6から、 \[ N q u \big( \vec{\mathstrut r} \big) = \varepsilon_0 \left( \varepsilon_r - 1 \right) E \big( \vec{\mathstrut r} \big) \] で、これに式1.9.4を代入すると、 \[ N q \frac{ -q E \big( \vec{\mathstrut r} \big) }{ m_{\rm e} \left( \omega^2 - {\omega_0}^2 \right) } = \varepsilon_0 \left( \varepsilon_r - 1 \right) E \big( \vec{\mathstrut r} \big) \\ \Leftrightarrow \quad \frac{ -N q^2 }{ m_{\rm e} \left( \omega^2 - {\omega_0}^2 \right) } = \varepsilon_0 \left( \varepsilon_r - 1 \right) \quad \Leftrightarrow \quad \varepsilon_r - 1 = \frac{ -N q^2 }{ m_{\rm e} \varepsilon_0 } \frac{ 1 }{ \omega^2 - {\omega_0}^2 } \\ \Leftrightarrow \quad \varepsilon_r = 1 - \frac{ N q^2 }{ m_{\rm e} \varepsilon_0 } \frac{ 1 }{ \omega^2 - {\omega_0}^2 } \] となりますけど。 | |
 | ここで、式1.8.5を思い出してもらうと、結局、 \[ \varepsilon_r \approx n^2 = 1 - \frac{ N q^2 }{ m_{\rm e} \varepsilon_0 } \frac{ 1 }{ \omega^2 - {\omega_0}^2 } \tag{1.9.7} \] が導けたことになります。 | |
 | そうか。周期\(T\)と波長\(\lambda\)の間には、 \[ \lambda = cT \tag{1.9.8} \] が成立するはずだし、式f1.1.10を考慮すれば、 \[ \omega = c \frac{ 2 \pi }{ \lambda } \quad \Leftrightarrow \quad \lambda = c \frac{ 2 \pi }{ \omega } \tag{1.9.9} \] になって\(\lambda\)と\(\omega\)は変換可能だから、式1.9.7は屈折率が波長に依存しているってことを意味しているわけですね。 | |
 | そういうことです。但し、式1.9.7は共振周波数が1つしかないものとして計算した結果です。ひょっとしたら、同じ種類の分子だけで構成されていても多くの共振周波数があるかもしれません。ですから、式1.9.7は、 \[ n^2 = 1 - \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{k}{} \frac{ {N_k}^2 }{ \omega^2 - {\omega_k}^2 } \tag{1.9.10} \] としておくべきでしょう。\(N_k\)は共振周波数\(\omega_k\)に対応する電子の数です。 | |
 | う。だんだん式がややこしくなってきた…。 | |
 | 更に、\(\omega \leq \omega_k\)のグループをa群、\(\omega>\omega_k\)のグループをb群として、式1.9.10を次のように変形しておきます。 \[ \begin{align*} n^2 &= 1 + \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^2 - \omega^2 } - \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{b}{} \frac{ {N_b}^2 }{ \omega^2 - {\omega_b}^2 } \\ &= 1 + \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^2 \left[ 1 - \left( \cfrac{\omega}{\omega_a} \right)^2 \right] }- \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{b}{} \frac{ {N_b}^2 }{ \omega^2 \left[ 1 - \left( \cfrac{\omega_b}{\omega} \right)^2 \right] } \end{align*} \] ここで、次のTaylor展開を用いると―。 \[ \frac{ 1 }{ 1 - x } = 1 + x + x^2 + x^3 + \cdots \] | |
 | ん~。 \[ \begin{align*} n^2 = 1 &+ \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^2 } \left[ 1 + \bigg( \frac{\omega}{\omega_a} \bigg)^2 + \bigg( \frac{\omega}{\omega_a} \bigg)^4 + \cdots \right] \\ &\quad \quad \quad \quad \quad - \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{b}{} \frac{ {N_b}^2 }{ \omega^2 } \left[ 1 + \bigg( \frac{\omega_b}{\omega} \bigg)^2 + \bigg( \frac{\omega_b}{\omega} \bigg)^4 + \cdots \right] \\ \end{align*} \] \[ \begin{align*} \phantom{n^2} = 1 &+ \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^2 } + \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^2 } \bigg( \frac{\omega}{\omega_a} \bigg)^2 + \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^2 } \bigg( \frac{\omega}{\omega_a} \bigg)^4 + \cdots \\ &\quad \quad \quad \quad \quad - \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{b}{} \frac{ {N_b}^2 }{ \omega^2 } - \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{b}{} \frac{ {N_b}^2 }{ \omega^2 } \bigg( \frac{\omega_b}{\omega} \bigg)^2 + \cdots \\ \end{align*} \] \[ \begin{align*} \phantom{n^2} = 1 &+ \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^2 } + \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^4 } {\omega}^2 + \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^6 } {\omega}^4 + \cdots \\ &\quad \quad \quad \quad \quad - \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{b}{} {N_b}^2 \frac{1}{ \omega^2 } - \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{b}{} {N_b}^2 {\omega_b}^2 \frac{1}{\omega^4} + \cdots \\ \end{align*} \] 式が複雑に…。 | |
 | ですが、\(\omega\)以外は定数扱いにできるので、 \[ A \equiv 1 + \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^2 } \quad B \equiv \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^4 } \quad C \equiv \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{a}{} \frac{ {N_a}^2 }{ {\omega_a}^6 } \quad \cdots \\ B^{\thinspace \prime} \equiv - \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{b}{} {N_b}^2 \quad C^{\thinspace \prime} \equiv - \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{b}{} {N_b}^2 {\omega_b}^2 \quad \cdots \] のように置けば―。 | |
 | こんな感じかな。 \[ n^2 = A + B {\omega}^2 + C {\omega}^4 + \cdots + \frac{ B^{\thinspace \prime} }{ \omega^2 } + \frac{ C^{\thinspace \prime} }{\omega^4} + \cdots \] | |
 | ここで、式1.9.9を代入すると?? | |
 | こうかな…。 \[ n^2 = A + B \left( c \frac{ 2 \pi }{ \lambda } \right)^2 + C \left( c \frac{ 2 \pi }{ \lambda } \right)^4 + \cdots + B^{\thinspace \prime} \left( \frac{ 1 }{ c } \frac{ \lambda }{ 2 \pi } \right)^2 + C^{\thinspace \prime} \left( \frac{ 1 }{ c } \frac{ \lambda }{ 2 \pi } \right)^4 + \cdots \] | |
 | つまり、\(n^2\)は定数項、及び\(\cfrac{1}{\lambda^2}\)、\(\cfrac{1}{\lambda^4}\)、\(\cfrac{1}{\lambda^6}\)、…、という項と、\(\lambda^2\)、\(\lambda^4\)、\(\lambda^6\)、…、という項の足し合わせで表現できるということです。特に、365nm≦\(\lambda\)≦1,014nmの範囲では、 \[ n^2 = A_0 + A_1 {\lambda}^2 + \frac{ A_2 }{ \lambda^2 } + \frac{ A_3 }{ \lambda^4 } + \frac{ A_4 }{ \lambda^6 } + \frac{ A_5 }{ \lambda^8 } \tag{1.9.11} \] という近似式でフィットすると比較的よく一致するということが経験的に知られており、式1.9.11をSellmeierの公式と言います(論文)。 | |
 | てことは、レンズ設計の際には、式1.9.11を使って、波長に応じて硝材の屈折率を計算しないといけないわけですね?? | |
 |
えぇ。ですから、レンズの硝材カタログには、必ずこの6つの係数が掲載されています。例えば、HOYA㈱の硝材カタログ・サイトを見ると、
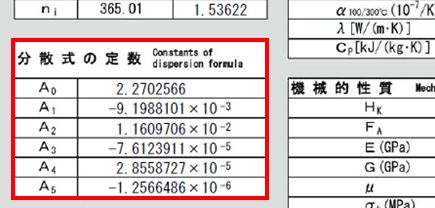 図1.9.3 BSC7のデータ抜粋(HOYA) こんな感じでデータが公開されているんですよ。㈱住田ガラス光学も同様ですね。 |
|
 |
教授。㈱オハラの硝材カタログ・サイトを見ると、式が違うんですけど。
 図1.9.4 ㈱オハラのSellmeierの公式 |
|
 | ㈱オハラはSchott AGに準拠してますからね。この式は、式1.9.10を、 \[ n^2 - 1 = \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \sum_{k}{} \frac{ {N_k}^2 }{ {\omega_k}^2 - \omega^2 } \] と書き換えて、\(k=3\)まででフィットすることを想定し、 \[ n^2 - 1 = \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \left[ \frac{ {N_1}^2 }{ {\omega_1}^2 - \omega^2 } + \frac{ {N_2}^2 }{ {\omega_2}^2 - \omega^2 } + \frac{ {N_3}^2 }{ {\omega_3}^2 - \omega^2 } \right] \] としてから、式1.9.9を代入するんです。 | |
 | そうすると…。 \[ \begin{align*} n^2 - 1 &= \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \left[ \frac{ {N_1}^2 }{ {\omega_1}^2 - \left( c \cfrac{2 \pi}{\lambda} \right)^2 } + \frac{ {N_2}^2 }{ {\omega_2}^2 - \left( c \cfrac{2 \pi}{\lambda} \right)^2 } + \frac{ {N_3}^2 }{ {\omega_3}^2 - \left( c \cfrac{2 \pi}{\lambda} \right)^2 } \right] \\ &= \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \left[ \frac{ \left( \cfrac{N_1}{\omega_1} \right)^2 \lambda^2 }{ \lambda^2 - \left( c \cfrac{2 \pi}{\omega_1} \right)^2 } + \frac{ \left( \cfrac{N_2}{\omega_2} \right)^2 \lambda^2 }{ \lambda^2 - \left( c \cfrac{2 \pi}{\omega_2} \right)^2 } + \frac{ \left( \cfrac{N_3}{\omega_3} \right)^2 \lambda^2 }{ \lambda^2 - \left( c \cfrac{2 \pi}{\omega_3} \right)^2 } \right] \end{align*} \] | |
 | はい。そのうえで、 \[ A_1 \equiv \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \left( \frac{ N_1 }{ \omega_1 } \right)^2 \quad A_2 \equiv \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \left( \frac{ N_2 }{ \omega_2 } \right)^2 \quad A_3 \equiv \frac{ q^2 }{ m_{\rm e} \varepsilon_0 } \left( \frac{ N_3 }{ \omega_3 } \right)^2 \\ B_1 \equiv \left( c \frac{ 2 \pi }{ \omega_1 } \right)^2 \quad B_2 \equiv \left( c \frac{ 2 \pi }{ \omega_2 } \right)^2 \quad B_3 \equiv \left( c \frac{ 2 \pi }{ \omega_3 } \right)^2 \quad \] のように置けば、㈱オハラが採用している式が導出できます。 \[ n^2 - 1 = \frac{ A_1 \lambda^2 }{ \lambda^2 - B_1 } + \frac{ A_2 \lambda^2 }{ \lambda^2 - B_2 } + \frac{ A_3 \lambda^2 }{ \lambda^2 - B_3 } \tag{1.9.12} \] | |
 | これもSellmeierの公式って言うんですか?? | |
 | そうですね。ですから、カタログを見るときは、どういう公式を使っているかをチェックしておかないといけません。いずれにしても、屈折率は波長依存性がありますから、例えばレンズの焦点距離などを図面で指定する場合には、どの波長で測定すべきなのか明記しておく必要があるのです。 | |
 | もし明記するのを忘れたら?? | |
 | ISOにより「e線で測る」というお約束になっています。 | |
 | e線って?? | |
 |
水銀の輝線スペクトルで、\(\lambda\)=546.07nmの光のことです。
 図1.9.5 水銀のアーク放電 |
|
 | 546.07nmと言うわりに、ぜんぜん緑色っぽく見えないんですけど。 | |
 |
水銀の輝線スペクトルは、546.07nmだけじゃないからです。それらが合わさったものが色として認識されるので、図1.9.5のように見えるんですよ。
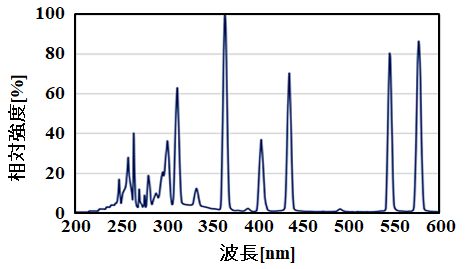 図1.9.6 水銀のスペクトル分布 |
|
 | 546.07nmだけじゃない?? | |
 | 図1.9.5はアーク放電したときの写真ですが、ガラスの中に水銀蒸気を封入して、両端から高い電圧をかけるんです(図1.9.7)。そうすると、負電極から電子がピュンピュン飛び出して、原子核を周回している電子にぶつかります(a)。このとき、その電子が弾き出されて励起状態になるんです(b)。 | |
 |
ビリヤードみたいなもの??
|
|
 |
そうですね。しかし、励起状態は不安定なので、弾き出された電子は元に戻ろうとします。このとき電磁波を放出するんですが、電子のエネルギー準位は決まっているので、その電磁波の波長は、電子の遷移に相当する固有値になっているというわけです(c)。
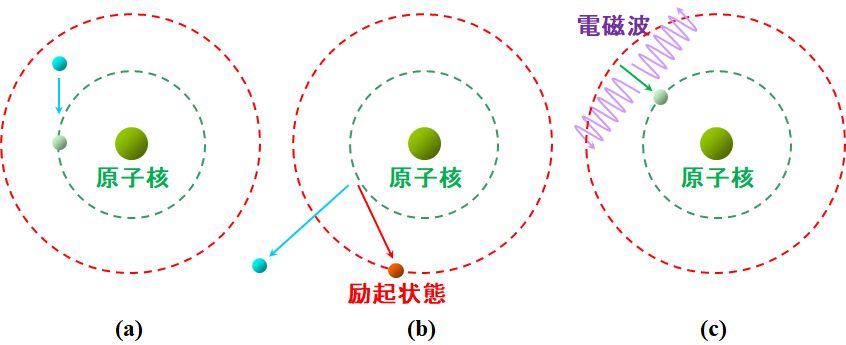 図1.9.7 輝線スペクトルのメカニズム 水銀の主なスペクトル線は、253.652nm、275.278nm、296.728nm、302.150nm、312.566nm、365.015nm、404.656nm、407.781nm、434.750nm、435.835nm、546.074nm、576.959nm、690.716nm、1013.980nmといったところでしょう。 |
|
 | ということは、どの軌道の電子が弾き出されるかは運次第だから、それに応じていろいろな波長の電磁波が放出されるってこと?? | |
 | そうです。図1.9.6は、そういうことを示しています。 | |
 | だったら、水銀ランプを使っても、e線での測定にはならないじゃないですか。 | |
 | ですので、e線以外の波長をカットする特別なフィルタを使います。 | |
 | そういうことか。 | |
 | そもそも、水銀をランプとして使うにしても、このままでは危険すぎますよ。 | |
 | ん??どうして?? | |
 | 紫外線が多く放出されているからです。特に253.652nmはUV-Cに分類され細胞を破壊しますし、UV-A(315nm~380nm)もUV-B(280nm~315nm)も多く含まれてますよね。紫外線ってお肌の大敵ではなかったでしたっけ?? | |
 | げげ。確かに。 | |
 | だから、水銀ランプはガラスの内側に塗料を塗ったりして使用するのが普通です。尤も、現在では水俣条約の影響でほぼ絶滅してしますけどね。ちなみに、オーロラは見たことありますか?? | |
 | 直接はないですけど、写真とかではありますよ。一度、実物を見たいとは思っているんですよねぇ。 | |
 | では、オーロラの色は?? | |
 | 色??う~ん、改めて訊かれると、何色だったかな…。 | |
 |
オーロラの色は緑色と相場が決まっています。
 図1.9.8 オーロラ |
|
 | 何で?? | |
 | オーロラ発生のメカニズムは、太陽風に含まれるプラズマ粒子が酸素原子とぶつかり、エキサイトした状態から元の安定状態に戻ろうとしたときに電磁波が放出されるというものです。酸素原子の輝線スペクトルが558nmなので、緑色なんですよ。 | |
 |
でも、ピンクのオーロラも見えるみたいですよ。
 図1.9.9 ピンク色のオーロラ |
|
 | それは、窒素分子の輝線スペクトルによるものですね。太陽風が強いときに見られます。 | |
 | とすると、地球を包む大気の組成が高度によって異なるってこと?? | |
 | そのとおりです。オーロラの発生する高度はKármánラインと呼ばれる100km上空ですが、その辺は酸素原子が多く分布しており、その層の内側は窒素分子が多く分布しています。太陽の活動が活発になると、深くまでプラズマ粒子が侵入してくるので、窒素分子を励起させることになるのです。 | |
 | 電子とかプラズマ粒子とか以外でも励起させることはできるんですか?? | |
 |
できますよ。例えば、熱エネルギーを与えてやれば、一般に炎色反応と呼ばれる現象が起こります。
 図1.9.10 炎色反応 |
|
 | あ、中学生のときに実験でやったなぁ。 | |
 | 炎色反応を示すのは、アルカリ金属、アルカリ土類金属、銅などの金属や塩ですが、メカニズムはまったく同じですね。これは花火の発色に応用されています。 | |
 |
そうなのかぁ。あれ、綺麗ですよね~。
|
|
 | 打ち上がった花火の色を見れば、赤色ならストロンチウム、黄色ならナトリウム、緑色ならバリウム、青色なら銅、っていう具合に原料が分かりますね。 | |
 | 教授は、そういうことを考えながら花火を見ているんですか?? | |
 | そうですよ。 | |
 | う~ん、教授とは一緒に花火を見に行きたくないですね…。 | |
 | …。 |
| 前頁へ | 戻る | 次頁へ |