 |
岝偑堎側傞攠幙偺嫬奅柺偱孅愜偡傞偲偄偆偺偼抦偭偰傑偡偐??
 恾1.8.1 岝偺孅愜 |
|
 |
Snell偺朄懃偱偡偹丅
 Willebrord Snell(1580乣1626) |
|
 |
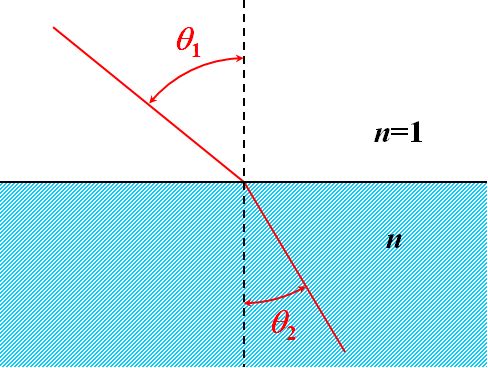
擖幩懁偺攠幙(=攠幙1)傪恀嬻(孅愜棪=\(1\))偲偟偨偲偒丄幃偱昞尰偟偰傒偰偔偩偝偄丅
 恾1.8.2 Snell偺朄懃 |
|
 | 攠幙2偺孅愜棪傪\(n\)丄擖幩妏傪\(\theta_1\)丄孅愜妏傪\(\theta_2\)偲偡傞偲丄 \[ n = \frac{ \sin \theta_1 }{ \sin \theta_2 } \tag{1.8.1} \] 偙偆偐側丅 | |
 | 婔壗岝妛偱偼丄孅愜棪偺掕媊偼Snell偺朄懃偦偺傕偺偵側傝傑偡丅偙傟傪攇摦岝妛揑側娤揰偱掕媊偟捈偟偰傒傑偟傚偆丅 | |
 | 攇摦岝妛偩偲掕媊偑曄傢傞傫偱偡偹?? | |
 |
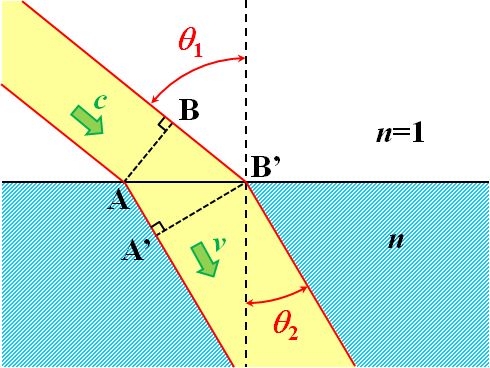
偼偄丅傑偢丄恾1.8.3傪尒偰偔偩偝偄丅
 恾1.8.3 孅愜棪傪嵞掕媊 |
|
 | 暯柺攇偑擖幩偟偰偄傞偭偰偙偲偱偡偹?? | |
 | 偦偆偱偡丅偱偼丄孅愜偟偨屻偺岝偼偳偆偱偡偐?? | |
 | 傗偭傁傝丄暯柺攇偩偲巚偄傑偡丅 | |
 | 偲偡傟偽丄A偲B丄A'偲B'偱埵憡偑惍崌偟偰側偄偲偍偐偟偄偱偡偹?? | |
 | 傫??埵憡偑惍崌偟偰偄傞丄偲偼?? | |
 |
椺偊偽丄幹暊儂乕僗傪巚偄晜偐傋偰偔偩偝偄丅
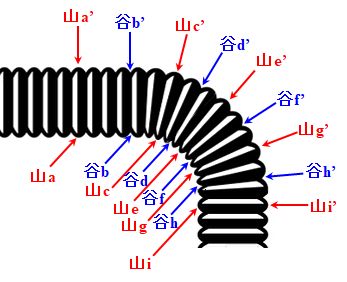 恾1.8.4 埵憡惍崌 偙偺偲偒丄恾1.8.4偺傛偆偵弅傫偱偄傞晹暘偲墑傃偰偄傞晹暘偱丄幹暊偺嶳偺売強(a偲a'丄c偲c'丄e偲e'丄g偲g'丄i偲i')丄扟偺売強(b偲b'丄d偲d'丄f偲f'丄h偲h')偼1懳1偵懳墳偟偰傑偡傛偹?? |
|
 | 傆傓傆傓丅 | |
 | 偙偆偄偆傛偆側忬嫷傪埵憡偑惍崌偟偰偄傞偲尵偆偺偱偡丅 | |
 | 側傞傎偳丅 | |
 | 偲偡傟偽丄恾1.8.3偵偍偄偰丄AA'偲BB'偺揱斃帪娫偼堦抳偟偰側偄偲偍偐偟偄偱偡丅 | |
 | 偮傑傝丄恀嬻拞偺岝懍\(c\)偵懳偟偰丄攠幙2偺岝懍傪\(v\)偲偡傞偲丄 \[ \frac{ \overline{\rm AA^{\thinspace \prime} } }{ v } = \frac{ \overline{\rm BB^{\thinspace \prime} } }{ c } \] 偲偄偆偙偲偱偡偹?? | |
 | 偙傟傪曄宍偡傞偲丄偙偆側傝傑偡丅 \[ \frac{ \overline{\rm AB^{\thinspace \prime}} \sin \theta_2 }{ v } = \frac{ \overline{\rm AB^{\thinspace \prime}} \sin \theta_1 }{ c } \quad \Leftrightarrow \quad \frac{ \sin \theta_2 }{ v } = \frac{ \sin \theta_1 }{ c } \quad \Leftrightarrow \quad \frac{ c }{ v } = \frac{ \sin \theta_1 }{ \sin \theta_2 } \tag{1.8.2} \] | |
 | 偍丅幃1.8.1偲幃1.8.2傪崌傢偣傞偲丄 \[ n = \frac{ c }{ v } \tag{1.8.3} \] 偩偐傜丄傂傚偭偲偟偰丄偙傟偑怴偟偄孅愜棪偺掕媊偩偭偨傝偟偰?? | |
 | 偦偆偱偡丅攇摦岝妛揑偵偼丄孅愜棪偼恀嬻拞偲攠幙拞偺岝懍偺斾偱掕媊偝傟傞偲偄偆偙偲偵側傝傑偡丅 | |
 | 偙偺懍搙偼埵憡懍搙偭偰偙偲偱偡偹丅 | |
 | 偼偄丅峏偵丄幃1.4.7偐傜丄 \[ n = \frac{ c }{ v } = \sqrt{ \frac{ \varepsilon \mu }{ \varepsilon_0 \mu_0 } } = \sqrt{ \varepsilon_r \mu_r } \tag{1.8.4} \] 偙偙偱丄\(\varepsilon_r=\cfrac{\varepsilon}{\varepsilon_0}\)丄\(\mu_r=\cfrac{\mu}{\mu_0}\)傪偦傟偧傟斾桿揹棪丄斾摟帴棪偲尵偄傑偡丅峏偵丄堦斒偵壜帇岝椞堟偵偍偄偰桿揹懱偺斾摟帴棪偼\(1\)側偺偱丄嬤帡揑偵偼偙偺傛偆偵彂偗傑偡丅 \[ n \approx \sqrt{ \varepsilon_r } \tag{1.8.5} \] | |
 | 偳偆偟偰丄斾摟帴棪偼\(1\)側傫偱偡偐?? | |
 | 偦偺棟桼偵偮偄偰偼屻傎偳愢柧偟傑偟傚偆丅 | |
 | 偁傟??傫??偪傚偭偲懸偭偰偔偩偝偄丅\(\varepsilon_r<1\)偩偲丄攠幙2偺岝懍偑\(c\)傛傝傕戝偒偔側傝傑偡偗偳?? | |
 | 偦偆偱偡偹丅 | |
 | 偊乣丅偦傟偭偰偍偐偟偔側偄偱偡偐??偩偭偰丄Einstein偺摿庩憡懳惈棟榑偵傛傟偽丄偄偐側傞傕偺傕岝懍傛傝懍偔堏摦偡傞偙偲偼偱偒側偄傫偱偡傛偹?? | |
 | 偦偆偱偡傛丅 | |
 | 偩偭偨傜丄柕弬偟偰傞偠傖側偄偱偡偐!! | |
 | 幚偼丄Einstein偑摿庩憡懳惈棟榑傪敪昞偟偨偲偒偺斀徹偲偟偰丄摨偠傛偆側媈媊傪掓偟偨尋媶幰偼偨偔偝傫偄傑偟偨丅 | |
 | 傎傜乣丅 | |
 |
偟偐偟丄偙偺柕弬偼Brillouin偵傛偭偰夝寛偝傟偰偄傑偡丅攇摦偺懍搙偵偼庬椶偑偁傞偲偄偆榖偼妎偊偰偄傑偡偐??
 Lèon Nicolas Brillouin(1889乣1969) |
|
 | 埵憡懍搙丄孮懍搙偭偰偄偆偺偼暦偒傑偟偨偗偳丅 | |
 | 偦偆偱偡丅偟偐偟丄傕偆1偮廳梫側懍搙偲偟偰攇摢懍搙偲偄偆偺偑偁傝傑偡丅捠忢丄恀嬻拞偺岝偺揱斃傪峫偊傞応崌丄偙傟傜偺嬫暿偼昁梫偁傝傑偣傫丅偦傕偦傕偺岆夝偼丄偙偺曈偺崿摨偐傜惗偠偰偄傞偲巚傢傟傑偡丅 | |
 | 攇摢懍搙??攇偺愭抂偺懍搙偭偰偙偲偱偡偐?? | |
 | 堄枴偼偦偆偱偡丅偦偟偰丄岝懍偱堏摦偡傞塢乆偲尵偭偨偲偒丄岝偲斾妑偝傟傞乽堏摦偡傞幚懱乿偲偼壗偐丄偲偄偆峫嶡偑廳梫偱丄偙偺媍榑偺拞偱偼丄偦偺娞怱側晹暘偑敳偗偰偄傑偡丅 | |
 | 幚懱??偆乣傫丅岝懍偱堏摦偟偰傎偟偄傕偺乧丅 | |
 | 偦傟偼忣曬偱偡丅偮傑傝丄忣曬偼岝懍傪挻偊偰揱払偝偣傞偙偲偑偱偒側偄丄偲夝庍偡傞偺偑惓偟偄丅 | |
 | 偲偄偆偙偲偼丄忣曬偺揱払偼丄埵憡懍搙丄孮懍搙丄攇摢懍搙偺偳傟偵娭楢偯偗傜傟傞偐丄偲偄偆栤戣偭偰偙偲?? | |
 |
偼偄丅忣曬偺揱払偲娭楢偡傞偺偼攇摢懍搙偩丄偲偄偆晹暘偑億僀儞僩偱偡丅Brillouin偑徹柧偟偨(榑暥)偺偼丄 丂嘆岝懍傪挻偊傞/挻偊側偄傪媍榑偡傞応崌偵偼丄攇摢懍搙傪懳徾偲偟側偗傟偽偄偗側偄 丂嘇攇摢懍搙偼岝懍傪挻偊傞偙偲偼側偄 丂嘊偩偐傜Einstein偺摿庩憡懳惈棟榑偵偼柕弬偼側偄 偲偄偆偙偲偱偡偹丅 |
|
 | 偲偄偆偙偲偼丄埵憡懍搙傕孮懍搙傕岝懍傪挻偊傞偙偲偑偁傝摼傞?? | |
 | 偁傝摼傑偡丅幚尡揑偵傕妋擣偝傟偰傑偡偟丅偲偼尵偭偰傕丄捠忢偺媍榑偵偍偄偰偼丄偦偆偄偆柺搢側偙偲偼弌偰偙側偄偺偱丄埵憡懍搙=孮懍搙=攇摢懍搙偲峫偊偰峔偄傑偣傫丅 | |
 | 偆乣傫丅Einstein傪挻偊傞nice側拝娽揰偲巚偭偨傫偩偗偳側偀丅 |
乣Fermat偺尨棟乣
 | 孅愜棪偵娭偡傞暿偺傾僾儘乕僠傕徯夘偟偰偍偒傑偟傚偆丅椺偊偽丄愳偱巕偳傕偑揗傟偰偄傑偡丅偳偆偟傑偟傚偆?? | |
 | 巹丄塲偓偵偼帺怣偁傝傑偡偐傜偹丅夆慠丄彆偗偵峴偒傑偡傛!! | |
 | 慺恖偑傓傗傒偵媬彆偵岦偐偆偲丄擇師嵭奞傪彽偔儕僗僋偑偁傞偺偱丄偙偺偲偒偺惓夝偼捈偪偵119斣偱偡偑丄崱夞偼摿椺慬抲偲偄偆偙偲偱恑傔傑偟傚偆丅 | |
 | 嫵庼偺島嵗偼摿椺慬抲偑懡偄偱偡偹丅 | |
 | 偝偰丄偱偒傞偩偗憗偔媬彆偵岦偐傢側偗傟偽偄偗傑偣傫丅偳偆偄偆儖乕僩傪偲傝傑偟傚偆偐?? | |
 |
巹偺偄傞埵抲A偲丄揗傟偰偄傞巕嫙偺埵抲B傪捈慄偱寢傫偩儖乕僩偠傖側偄偱偡偐??偦傟偑嵟抁偱偡偟丅
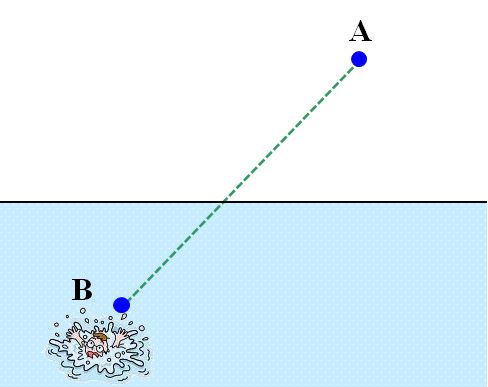 恾1.8.5 嵟抁帪娫宱楬栤戣(1) |
|
 | 偱傕丄塲偖僗僺乕僪傛傝丄憱傞僗僺乕僪偺曽偑懍偄偱偡傛偹丅偲偡傟偽丄塲偖嫍棧偼抁偄曽偑傛偔側偄偱偡偐?? | |
 |
偆乣傫丅尵傢傟偰傒傟偽偦偆偱偡偹丅偦偆偡傞偲丄恾1.8.6??
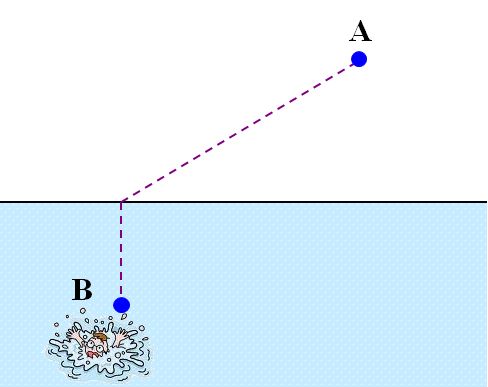 恾1.8.6 嵟抁帪娫宱楬栤戣(2) |
|
 | 恾1.8.6偩偲丄嫍棧偑怢傃偡偓偰晄棙偠傖側偄偱偡偐偹?? | |
 |
側傞傎偳乧丅偲偡傟偽丄奣偹恾1.8.7傒偨偄側姶偠??
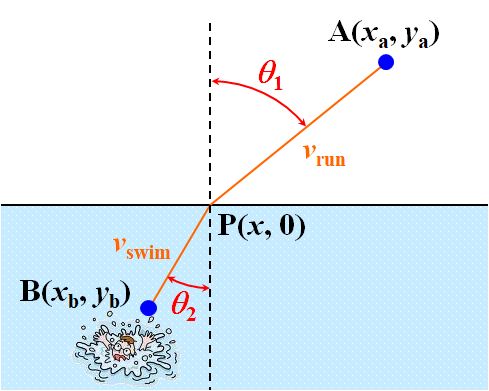 恾1.8.7 嵟抁帪娫宱楬栤戣(3) 偱傕丄P偺埵抲偼傛偔暘偐傜側偄偱偡偗偳丅 |
|
 | 偱偼丄揰P傪悢妛揑偵媮傔偰傒傑偟傚偆丅傑偢丄揰A仺揰P仺揰B偵妡偐傞帪娫\(t\)傪媮傔偰偔偩偝偄丅 | |
 | 傫乣偲丅 \[ t = \frac{ \overline{\rm AP} }{ v_{\rm run} } + \frac{ \overline{\rm PB} }{ v_{\rm swim} } = \frac{ \sqrt{ \left( x_{\rm a} - x \right)^2 + {y_{\rm a}}^2 } }{ v_{\rm run} } + \frac{ \sqrt{ \left( x - x_{\rm b} \right)^2 + {y_{\rm b}}^2 } }{ v_{\rm swim} } \] | |
 | 師偼丄\(x\)偱旝暘偱偡丅 | |
 | 偙偆偐側丅 \[ \frac{ dt }{ dx } = - \frac{ x_{\rm a} - x }{ v_{\rm run} \sqrt{ \left( x_{\rm a} - x \right)^2 + {y_{\rm a}}^2 } } + \frac{ x - x_{\rm b} }{ v_{\rm swim} \sqrt{ \left( x - x_{\rm b} \right)^2 + {y_{\rm b}}^2 } } \] | |
 | \(\theta_1\)偲\(\theta_2\)傪巊偭偰昞尰偱偒傑偣傫偐?? | |
 | 偁丄偱偒傑偡偹丅 \[ \frac{ dt }{ dx } = - \frac{ \sin \theta_1 }{ v_{\rm run} } + \frac{ \sin \theta_2 }{ v_{\rm swim} } \] | |
 | 嵟抁帪娫傪媮傔傞偺偼嬌抣栤戣偱偡偐傜丄\(\cfrac{dt}{dx}=0\)傪夝偗偽丄揰P偑枮偨偡傋偒忦審偑摼傜傟傑偡丅 | |
 | 偮傑傝丄 \[ 0 = - \frac{ \sin \theta_1 }{ v_{\rm run} } + \frac{ \sin \theta_2 }{ v_{\rm swim} } \quad \Leftrightarrow \quad \frac{ \sin \theta_1 }{ v_{\rm run} } = \frac{ \sin \theta_2 }{ v_{\rm swim} } \quad \Leftrightarrow \quad \frac{ \sin \theta_1 }{ \sin \theta_2 } = \frac{ v_{\rm run} }{ v_{\rm swim} } \] 嫵庼丅偙傫側寁嶼偟偰偄傞娫偵丄巕偳傕偼揗巰偡傞傛偆偵巚偆傫偱偡偗偳乧丅 | |
 | 傑丄偦傟偼偦偆側傫偱偡偑丄偙偺幃偲幃1.8.2傪斾妑偟偰傒偰偔偩偝偄丅 \[ \frac{ c }{ v } = \frac{ \sin \theta_1 }{ \sin \theta_2 } \tag{1.8.2} \] | |
 | 偆乣傫乧丅傫??偁傟??偦偭偔傝偱偡偹丅 | |
 | 偮傑傝丄偙偙偱暘偐偭偨偙偲偼丄揰A偲揰B傪嵟抁帪娫偲偄偆忦審壓偱寢傏偆偲偡傞偲丄Snell偺朄懃偑摫偐傟傞偲偄偆偙偲偱偡丅傕偭偲尵偊偽丄岝偼弖帪偵嵟抁帪娫偲側傞宱楬傪慖戰偟偰揱斃偡傞偺偱偡丅 | |
 | 岝偺曽偑偢偭偲尗偄偭偰偙偲偠傖側偄偱偡偐!! | |
 |
偲偄偆偐丄帺慠偼偦偺傛偆偵愝寁偝傟偰偄傞傜偟偄丄偲偄偆偙偲偱偡傛丅偙傟傪敪尒幰偺柤慜傪偲偭偰Fermat偺尨棟偲尵偄傑偡丅
 Pierre de Fermat(1607乣1665) |
|
 | 尨棟乗丅偭偰偙偲偼丄偳偆偟偰偦偆側偭偰偄傞偺偐丄偲偄偆偙偲偼愢柧偱偒側偄傫偱偡偹?? | |
 | 偼偄丅偟偐偟丄偙傟傪庴偗擖傟傞偲丄孅愜棪偑嬒堦側嬻娫偱偼岝偼捈恑偡傞偲偐丄斀幩偡傞偲偒偼擖幩妏偲斀幩妏偑摍偟偔側傞丄偲偄偭偨堦楢偺朄懃偑丄偁傞堄枴丄昁慠偺偙偲偲偟偰摫偔偙偲偑偱偒傑偡丅 | |
 | 偆乣傫丅妋偐乧偵乗丅傫??嫵庼丅Fermat偺尨棟丄壗偐曄偱偡傛丅 | |
 | 曄偱偡偐?? | |
 | 偩偭偰丄岝偑嵟抁帪娫偺宱楬傪慖戰偡傞偨傔偵偼丄嫬奅柺偺愭偺忣曬傪抦偭偰偍偔昁梫偑偁傞偠傖側偄偱偡偐丅偳偆偟偰丄岝偼孅愜棪偺忣曬偑暘偐傞傫偱偡偐?? | |
 | 側傞傎偳丅側偐側偐塻偄巜揈偱偡偹丅 | |
 | 偱偟傚?? | |
 | 偨偄偰偄偺恖偼丄埲忋偺愢柧偱擺摼偡傞傫偱偡偑丄偦偆偼偄偒傑偣傫偐丅 | |
 | 巹偼閤偝傟傑偣傫傛乣丅 | |
 |
閤偡偮傕傝偼栄摢側偄偺偱偡偑丄妋偐偵偦偺媈栤偼崌棟惈偑偁傞傛偆偵傕巚偊傑偡丅偱偼丄偦偺媈栤傪夝徚偡傞偨傔偵丄埲壓偺傛偆側偙偲傪峫偊偰傒傑偟傚偆丅2師尦揑偵懆偊傞偲丄岝尮S偐傜曻幩偟偨岝偼摨怱墌忬偵峀偑偭偰偄偒傑偡偐傜丄偦偺岝偼嫬奅柺偺P1偵嵟弶偵摓払偡傞丄偙偙傑偱偼偄偄偱偡傛偹??
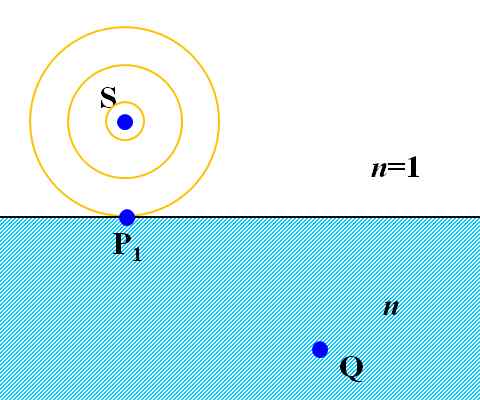 恾1.8.8 岝尮S偺攇柺偼丄嵟弶偵P1偵摓払偡傞 |
|
 | 偄偄偱偡傛丅 | |
 |
偦偟偰丄帪娫偑宱偮偵廬偄丄P2丄P3丄乧丄P6丄乧偲偄偆傛偆偵丄楢懕揑偵嫬奅柺偵攇柺偑摓払偟傑偡丅峏偵丄Huygens偺尨棟偵傛傟偽丄揰P傪壖憐揑側攇尮偲偟偰丄戞2師攇偑惗偠傑偡丅
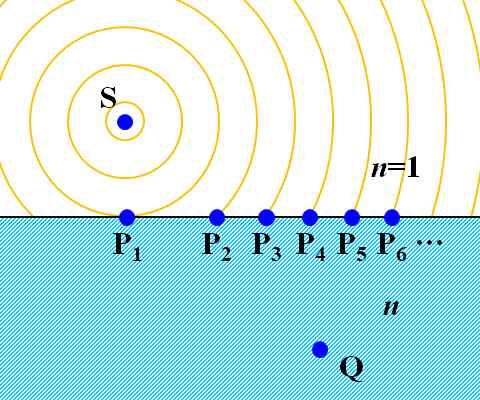 恾1.8.9 帪娫偑宱偮偲丄岝尮S偺攇柺偼丄嫬奅柺偵師乆偵摓払偡傞 P1傪攇尮偲偟偨戞2師攇偼丄偄偢傟揰Q偵摓払偡傞偺偼偄偄偱偡偐?? 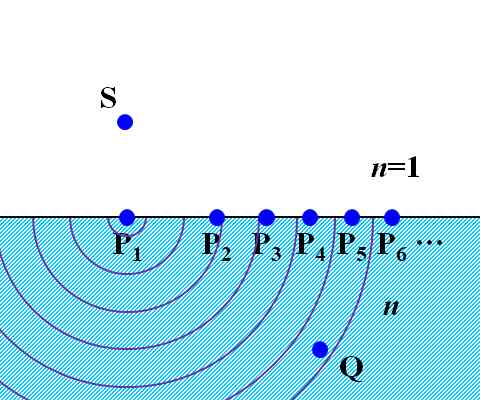 恾1.8.10 P1傪攇尮偲偟偨戞2師攇偼丄揰Q偵摓払偡傞 |
|
 | OK偱偡丅 | |
 |
摨條偵丄P2傪攇尮偲偟偨戞2師攇傕丄偄偢傟揰Q偵摓払偟傑偡丅偙傟偼丄嫬奅柺忋偺偡傋偰偺揰P偵偮偄偰尵偊傞偙偲偱偡丅
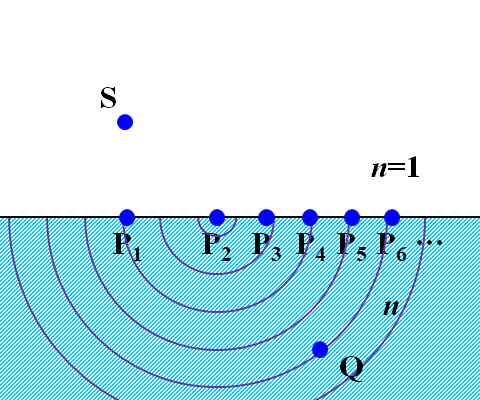 恾1.8.11 P2傪攇尮偲偟偨戞2師攇偼丄揰Q偵摓払偡傞 偦偆偡傞偲丄摉慠丄岝尮S仺嫬奅柺P仺揰Q偺僷僗偺偆偪丄嵟抁帪娫偺僷僗偑1偮寛傑傞偼偢偱偡丅偦偟偰丄偦偺僷僗偺忣曬傪僉儍僢僠偟偨傜丄偦傟埲奜偺忣曬偼柍帇偝傟傞丄偲峫偊傟偽帺慠側宍偱Fermat偺尨棟傪夝庍偡傞偙偲偑偱偒傑偡丅 |
|
 | 岝偼Snell偺朄懃側傫偰抦傜側偄偗偳丄寢壥偲偟偰Snell偺朄懃偵側偭偰傑偟偨丄偭偰偙偲偱偡偹?? | |
 | 偦偆偱偡丅Fermat偺尨棟偑偁傞偐傜Snell偺朄懃偑惉棫偡傞偺偱偼側偔丄Fermat偺尨棟偼寢壥榑傪弎傋偰偄傞偵偡偓側偄丄偲偄偆夝庍偱偡丅 | |
 | 偆乣傫丅妋偐偵丄偦偺愢柧偩偲丄偦偺偲偍傝側傫偩偗偳丄壗偱嵟抁帪娫偺宱楬埲奜偺忣曬偼柍帇偝傟偪傖偆傫偱偡偐?? | |
 | 偦偆偄偆傆偆偵帺慠偑愝寁偝傟偰偄傞偐傜丄偲尵偆偙偲傕偱偒傑偡偟丄椺偊偽僉儍僢僠偟偨偺偑恖娫偺栚偩偲偡傞偲丄嵟抁帪娫偺宱楬埲奜偺忣曬偼晄梫側偺偱丄擼偺曽偱柍帇偡傞張棟傪峴偭偰偄傞丄偲峫偊傞偙偲傕偱偒傑偡丅嵟抁帪娫偺宱楬埲奜偺忣曬偼柍帇偡傞傛偆偵擼偑恑壔偟偨丄偲偄偆偙偲偱偡偹丅 | |
 | 偊??偦偆側傫偱偡偐?? | |
 | 偦傟偼暘偐傝傑偣傫丅偦偆偄偆峫偊曽傕偱偒傞丄偲偄偆偙偲偱偡丅 | |
 | 暔棟妛偵丄恖娫偺擣抦偺榖傪帩偪崬傓偺偼丄僘儖偄傛偆偵巚偄傑偡丅 | |
 | 僘儖偄偱偡偐乧丅偁偔傑偱暔棟妛偺悽奅偩偗偱愢柧偟傛偆偲偡傞偲丄峏偵検巕椡妛偺奣擮傪帩偪崬傓偟偐側偄偱偟傚偆偹丅 | |
 | 検巕椡妛偩偭偨傜丄壜擻側傫偱偡偐?? | |
 |
擺摼偱偒傞偐偳偆偐偼暘偐傜側偄偱偡偑丄Feynman偑傕偭偲戝抇側愢柧傪偟偰偄傑偡丅
 Richard Phillips Feynman(1918乣1988) |
|
 | 偙偺恖偺敪憐偼丄偄偮傕戝抇側婥偑偟傑偡偗偳乧丅 | |
 | 偦偆偱偡偹丅傑偢丄億僀儞僩偲偟偰墴偝偊偰偍偔傋偒側偺偼丄検巕椡妛偵偍偄偰丄棻巕偑偳偙偵懚嵼偡傞偐偼妋棪暘晍偱偟偐昞尰偱偒側偄丄偲偄偆揰偱偡丅 | |
 | 偁乣丄偙傟偱偡傛丅偙偆偄偆峫偊曽傪偡傞偐傜丄検巕椡妛偑僀儅僀僠撻愼傔側偄傫偱偡傛偹偉丅 | |
 | 傑偀丄偦偙偼堦扷丄妱傝愗偭偰偔偩偝偄丅偦偺偆偊偱丄Feynman偼丄検巕椡妛揑側娤揰偐傜丄岝尮S偐傜曻幩偝傟傞岝巕偼丄偁傜備傞宱楬傪偲傞丄偲峫偊傞偺偱偡丅 | |
 | 偁傜備傞?? | |
 | 偦偆偱偡丅 | |
 | 柍悢偵偁傝傑偡偗偳丅 | |
 | 偦偆偱偡丅 | |
 | 椺偊偽丄塅拡偺壥偰傑偱峴偔岝巕傕偁傝摼傑偡傛偹?? | |
 | 偦偆偱偡偹丅栟傕丄塅拡偵壥偰偑偁傟偽丄偺榖偱偡偑丅 | |
 | 椺偊偽丄偦偺応偱壗搙傕僋儖僋儖夞揮偟偰偄傞岝巕偲偐丄壗搙傕棫偪巭傑傞傛偆側岝巕傕偁傝傑偡偗偳?? | |
 | 偦傟傕OK偱偡丅 | |
 | 偆乣傫丅妋偐偵戝抇偱偡偹乣丅偱傕丄晽楥晘傪峀偘傞偩偗峀偘偰丄廂廍偑偮偐側偔側傞傫偠傖側偄偱偡偐?? | |
 | 偦偙偑丄揤嵥偺揤嵥偨傞強埲偱偟偰偹丅壗偲丄偦偺偡傋偰偺宱楬傪懌偟崌傢偣傞偺偱偡丅 | |
 | 柍悢偵偁傝傑偡偗偳??懌偣傞傫偱偡偐?? | |
 | 悢妛揑側徻嵶偼徣偒傑偡偑丄懌偣傑偡丅偦偆偡傞偲丄偁傜備傞宱楬偺懚嵼妋棪偑寁嶼偝傟傑偡丅 | |
 | 壗偲!! | |
 | 偦偟偰丄偦偺懚嵼妋棪偼丄嵟抁帪娫嬤朤偺僷僗偑巟攝偟偰偄傞丄偲偄偆偺偑Feynman偺峫偊曽偱偡丅 | |
 | 尵偭偰偄傞偙偲偑暘偐傝傑偣乣傫丅 | |
 | 尵偄姺偊傞偲丄嵟抁帪娫廃曈偺僷僗偑丄嵟傕懚嵼妋棪偑崅偄丄偲偄偆偙偲偱偡傛丅 | |
 | 偆乣傫丅偰偙偲偼丄嵟抁帪娫偩偗偠傖側偔偰丄偦傟偵嬤偄僷僗傕娤應偱偒傞偭偰偙偲偵側傝傑偣傫偐?? | |
 | 偦偆偱偡偹丅 | |
 | 傫??偦傟偳偙傠偐丄懠偺僷僗偼掅偄妋棪偩偗偳懚嵼偡傞偭偰偙偲偵傕側傝傑偡傛偹?? | |
 | 偦偆偱偡偹丅 | |
 | 偊乣丅偩偭偰丄孅愜揰偭偰丄Snell偺朄懃傪枮偨偡1揰偟偐側偄偠傖側偄偱偡偐乣丅 | |
 | 側傞傎偳丅偟偐偟丄偦傟偼丄偦傕偦傕岝慄偲偄偆傕偺偺懚嵼傪壖掕偟偨偲偒偵惉棫偡傞榖偱偡傛偹?? | |
 | 偦偆偱偡傛丅 | |
 | 偱傕丄傛偔峫偊偰傒偰偔偩偝偄丅攇摦岝妛揑偵偼丄偦傕偦傕岝慄側偳偲偄偆傕偺偼懚嵼偟傑偣傫丅 | |
 | 儉儉儉丅 | |
 | 偦傫側傕偺偼丄嬌傔偰恖娫揑偱拪徾搙偺崅偄奣擮偱偟偐側偄偺偱偡丅 | |
 | 偦傟偼丄偦偆偩偗偳丅 | |
 | 埲慜丄暔棟妛偼丄恖娫偑帺慠傪棟夝偡傞偨傔偺儌僨儖偺峔抸偩丄偲尵偄傑偟偨丅 | |
 | 偦偆偱偟偨偹丅 | |
 |
旝彫側悽奅偱偼丄棻巕偺懚嵼傪妋棪暘晍偲偟偰昞尰偡傞偲棟夝偟傗偡偄丄偲偄偆偺偑検巕椡妛偺儌僨儖偱偡丅傛偭偰丄検巕椡妛揑側昞徾偱偼丄岝慄傕妋棪榑偱懆偊傞昁梫偑偁傞偟丄岝巕偺懚嵼妋棪偺嵟傕崅偄婳愓偑婔壗岝妛偱尵偆岝慄偱偁傞丄偲掕媊偟捈偡偺偼丄晄巚媍偱傕壗偱傕側偔丄擩傠崌棟揑側夝庍偩偲尵偊傞偱偟傚偆丅
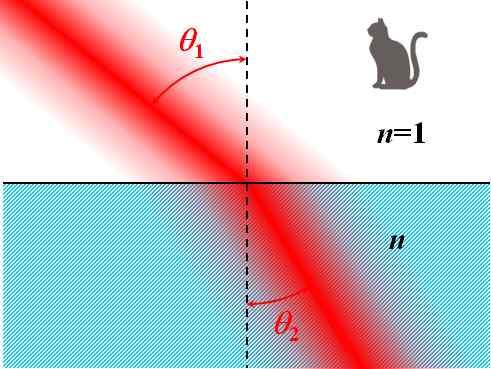 恾1.8.12 検巕椡妛揑偵惓偟偄Snell偺朄懃偺僀儊乕僕恾(愒怓偑擹偄=岝巕偺懚嵼妋棪偑崅偄) |
|
 | 偆乣傫丅壗偐娵傔崬傑傟偨姶偠偑偟傑偡偗偳乧丅偱傕丄晛捠偼検巕椡妛偺儌僨儖側傫偰弌偰偒傑偣傫傛偹?? | |
 | 偳偺儌僨儖傪嵦梡偡傞偐偼丄媍榑偡傞懳徾偺儗儀儖偱曄偊傟偽偄偄傫偱偡丅偦傟傎偳崅搙側儗儀儖偺媍榑偱側偄偲偙傠偵丄検巕椡妛偺儌僨儖傪梡偄偰丄榖傪傗傗偙偟偔偡傞昁梫偼偁傝傑偣傫傛偹??偦傟偼丄Newton椡妛偱帠懌傝傞媍榑偵丄偁偊偰Einstein曽掱幃傪帩偪崬傑側偄偺偲摨偠偙偲偱偡丅 | |
 | 妋偐偵丅 | |
 | 偙偙偱偼丄Feynman偺峫偊曽偺怗傝傪徯夘偟傑偟偨偑丄亀嫊悢偺忣弿亁偲偄偆杮偱偼丄傕偆彮偟摜傒崬傫偩愢柧傪撉傓偙偲偑偱偒傑偡丅 | |
 | 偊乣丄偙傟丄1,000儁乕僕偔傜偄偁傞傫偱偡偗偳丅 | |
 | 偱傕丄暋嶨側寁嶼幃偑師偐傜師傊墴偟婑偣偰偔傞愱栧彂偲偼堘偭偰丄撉傒傗偡偄偱偡傛丅 | |
 | 杮摉偱偡偐?? | |
 | 拞妛惗傪懳徾偲偟偰偄傞傛偆偱偡偟丅 | |
 | 杮摉偱偡偐?? | |
 | 寶慜忋偼丅 | |
 | 傎傜乣丅 | |
 | 偟偐偟丄暔帠偺摴棟傪妝偟偰棟夝偟傛偆偲偡傞曽偑娫堘偭偰傑偡丅 | |
 | 妛栤偵墹摴側偟?? | |
 | 偦偆偄偆偙偲偱偡丅 | |
 | Feynman偼丄偳偆偟偰丄偙傫側敪憐傪偟偨傫偱偡偐偹?? | |
 | 慜婜検巕榑偲屇偽傟傞廬棃偺検巕椡妛揑側奣擮偵擺摼偱偒側偐偭偨偐傜偱偡偹丅偩偐傜丄帺暘棳偺怴偟偄夝庍傪嶌傝弌偟偨傫偱偡傛丅偙偺峫偊偼丄宱楬愊暘偲偄偆曽朄偵廂澥偝傟傑偡(榑暥)丅 | |
 | 偱傕丄偡傋偰偺宱楬傪嫋梕偟偰丄偦傟傪懌偟崌傢偣傞側傫偰丄偦偆娙扨偵庴偗擖傟傜傟側偄敪憐偱偡傛偹丅 | |
 | 偼偄丅偩偐傜丄摉弶偼暔棟妛夛偐傜丄扨側傞偛搒崌庡媊偺寁嶼庤朄偵偡偓側偄丄偲偄偆庴偗巭傔曽傪偝傟偰偄偨傛偆偱偡偹丅 | |
 | 傗偭傁傝丅 | |
 | 偲偙傠偑丄偦偺屻丄宱楬愊暘傪儀乕僗偵偟偨Feynman僟僀傾僌儔儉偲偄偆怴偟偄庤朄傪揥奐偟(榑暥)丄慺棻巕偺怳傞晳偄偑娙曋偵婰弎偱偒傞偙偲偑擣抦偝傟傞偲丄晽岦偒偑僈儔僢偲曄傢傞偺偱偡丅 | |
 | 傊偉丅 | |
 | 崱傗丄慺棻巕偺怳傞晳偄傪棟夝偡傞偺偵丄Feynman僟僀傾僌儔儉偼晛捠偵巊傢傟偰傑偡偐傜偹丅偝偰丄Fermat偺尨棟傪掕幃壔偟偰偍偒傑偟傚偆丅揰A偐傜揰B傑偱偵妡偐傞帪娫\(t\)偼丄岝楬挿偺慄梫慺傪\(dl\)偲偡傞偲丄 \[ t = \int_{\rm A}^{\rm B} \frac{ dl }{ v } \] 偲彂偗傑偡偑丄椉曈偵\(c\)傪妡偗偰丄 \[ ct = \int_{\rm A}^{\rm B} \frac{ c }{ v } dl = \int_{\rm A}^{\rm B} n dl \tag{1.8.6} \] 偲側傝丄偙偺嬌抣偑\(0\)偲偄偆偙偲偱偡偐傜丄 \[ \delta \int_{\rm A}^{\rm B} n dl = 0 \tag{1.8.7} \] 偲側傝傑偡丅 | |
 | \(\delta\)?? | |
 | 偮傑傝丄揰A偲揰B傪寢傇宱楬傪彮偟偩偗偢傜偟偰傒傞偲偄偆偙偲偱偡丅偦傟偱傕\(t\)偺曄壔偑\(0\)偱偁傟偽丄偦傟偼嬌抣偲偄偆偙偲偩偐傜丄偦傟偙偦偑媮傔傞宱楬偱偁傞丄偲偄偆堄枴偱偡偹丅 | |
 | Fermat偭偰丄悢妛偱偼昿斏偵搊応偟傑偡傛偹丅 | |
 | 偦偆偱偡偹丅偱傕丄Fermat偼尦乆嵸敾姱偱偡丅 | |
 | 偊??悢妛幰偱傕暔棟妛幰偱傕側偄傫偩丅 | |
 | 摉帪偺僼儔儞僗偺朄棩偱偼丄曎岇巑傗嵸敾姱偼丄榙楪傪傕傜偭偰検孻偵庤怱傪壛偊傞婋尟傪夞旔偡傞偨傔丄堦斒恖偲偺愙怗偑嬛偠傜傟偰偄傑偟偨丅偩偐傜丄巇帠偑廔傢傞偲堦攖堸傒偵峴偔傢偗偵傕偄偐偢丄栭偼壣偱壣偱偟傚偆偑側偄丅偦偺帪娫捵偟偺偨傔偵Fermat偼悢妛傪尋媶偟偰偄偨偺偱偡丅 | |
 | 庯枴?? | |
 | 偦傫側偲偙傠偱偟傚偆偹丅偙偺恖偼丄帺暘偺巚偄晅偒傪悢妛偺嫵壢彂偺梋敀偵彂偔暼偑偁偭偨傫偱偡偑丄Gauss偲偼恀媡偱丄巆擮側偑傜尩枾偵徹柧偡傞偙偲偵偼嫽枴偑偁傝傑偣傫偱偟偨丅桳柤側Fermat偺嵟廔掕棟偼抦偭偰偄傞偱偟傚偆?? | |
 | 3埲忋偺帺慠悢\(n\)偵偮偄偰丄\(x^n+y^n=z^n\)偲側傞帺慠悢偺慻\((x,y,z)\)偼懚嵼偟側偄丄偭偰傗偮偱偡偹丅 | |
 |
偦傟傕丄娞怱偺徹柧偼側偔丄乽偙偺掕棟偵娭偟偰丄梋偼恀偵嬃偔傋偒徹柧傪尒偮偗偨偑丄偙偺梋敀偼偦傟傪彂偔偵偼嫹偡偓傞乿偲彂偄偰廔傢偭偰偄傞偺偱偡丅
 恾1.8.13 Fermat偺嵟廔掕棟偺捈昅偺彂偒崬傒 |
|
 | 梋敀丄寢峔偁傝偦偆偱偡偗偳偹乧丅 | |
 |
偙偺掕棟偼360擭傕宱偭偰丄Andrew Wiles偵傛偭偰峬掕揑偵夝寛偝傟傑偡(榑暥)丅
 Andrew John Wiles(1953乣) |
|
 | 偰偙偲偼丄悢妛偺丄偊乣偲丄僼傿乧僼傿乧丅 | |
 | 僼傿乕儖僘徿偱偡偐?? | |
 | 偁乣丄偦傟偦傟丅僼傿乕儖僘徿傪get偟偨傫偱偡偹?? | |
 | 僼傿乕儖僘徿偼僲乕儀儖徿傛傝傕忦審偑尩偟偄偱偡丅擭楊惂尷偑偁傝傑偡偟偹丅 | |
 | 壗嵨傑偱偱偡偐?? | |
 | 40嵨埲壓偱側偄偲丄庴徿偱偒傑偣傫丅 | |
 | Wiles偑徹柧偟偨偺偼?? | |
 | 巆擮側偑傜42嵨偱偟偨丅 | |
 | 惿偟偄乣!! | |
 | 徹柧偵偼旕忢偵崅搙側悢妛偑巊傢傟偰偄傞偺偱丄尰嵼偱偼丄Fermat偺梋敀偺彂偒崬傒偼僴僢僞儕偩傠偆丄偲偄偆偺偑堦斒揑側尒曽偱偡偹丅 | |
 | Fermat偺尨棟偭偰丄偲偰傕恄旈揑偱柺敀偄偲巚偆偗偳丄壗偐墦傑傢傝偱偡偹丅 | |
 | 妋偐偵丄偦偆巚偊傑偡偑丄暔棟妛揑偵偼Fermat偺尨棟偺曽偑杮幙側傫偱偡丅 | |
 | 偱傕丄偦偙偐傜摫偐傟傞偺偑岝妛偵尷掕偝傟偰偄傞傫偠傖丄尨棟偲屇傇偵偼僔儑儃偔側偄偱偡偐?? | |
 |
偲偙傠偑丄偙傟偲帡偨傛偆側尨棟偑椡妛偺曽偐傜傕妋棫偝傟傑偡(榑暥)丅偦傟傪Maupertuis偺尨棟偲尵偄傑偡丅
 Pierre-Louis Moreau de Maupertuis(1698乣1759) 偙傟傜偺峫偊曽偼嵟廔揑偵嵟彫嶌梡偺尨棟偲偄偆宍偵傑偲傔傜傟丄Lagrange傗Jacobi丄Hamilton偲偄偭偨恖偨偪偵傛傝曄暘尨棟傊偲敪揥偡傞偺偱偡丅  Carl Gustav Jacob Jacobi(1804乣1851) |
|
 | 偦偆偄偆偙偲偐乧丅 | |
 | 曄暘尨棟偼暔棟妛偵偍偄偰嵟嫮偺峫偊曽偱丄偙傟傪梡偄傟偽Maxwell曽掱幃傕Einstein曽掱幃傕摫弌偡傞偙偲偑偱偒傑偡丅 | |
 | 偊??偦偆側傫偱偡偐??偩偭偨傜丄曄暘尨棟偺曽傪嫵偊偰偔偩偝偄傛乣丅 | |
 | 暿偵偄偄偱偡偑丄埖偆悢妛偼奿抜偵擄偟偔側傝傑偡傛丅 | |
 | 偊?!?!偳偺偔傜偄?? | |
 | 偙傟傑偱傛傝傕僊傾偑3偮偔傜偄丄偁偑傝傑偡偐偹丅 | |
 | 乧丅偠傖偀丄偄偄偱偡丅 | |
 | 偦傕偦傕丄嵟彫嶌梡偺尨棟偺"嶌梡"偭偰偄偆偺偑壗偩偐暘偐傜側偄偱偟傚偆?? | |
 | 傑偀丄偦偆偱偡偹丅 | |
 | 擩傠丄曄暘尨棟偱廳梫側偺偼丄椺偊偽Maxwell曽掱幃側傜丄偦偺曽掱幃傪婰弎偱偒傞"嶌梡"傪扵偡偙偲側傫偱偡丅偟偐偟丄巆擮側偑傜丄"嶌梡"偺忋庤偄扵偟曽偼偁傝傑偣傫丅 | |
 | 側乣傫偩丅悽偺拞丄娙扨偵偼偄偐側偄傕偺偱偡偹丅 | |
 | 偪側傒偵丄恀嬻拞(嬻婥拞)偐傜悈拞偵岝傪擖幩偡傞偲丄昁偢\(\theta_1>\theta_2\)偵側傞偺偱丄\(\sin\theta_1>\sin\theta_2\)偱偡丅傛偭偰丄幃1.8.2偐傜\(c>v\)側偺偱丄Fermat偼乽岝懍偼悈拞偺曽偑抶偔側傞乿偲梊尵偟傑偟偨丅偙偺梊尵偼丄岝偼攇摦偱偁傞偲峫偊傞偲忋庤偔愢柧偱偒傞偺偱丄Fermat偼攇摦愢偺僗僞儞僗偩偲尵偊傑偡丅 | |
 | 側傞傎偳丅 | |
 |
偟偐偟丄Fermat偲摨帪戙偵妶桇偟偰偄偨揘妛幰偺Descartes偼乽岝懍偼悈拞偺曽偑懍偔側傞乿偲梊尵偟傑偡丅
 Renè Descartes(1596乣1650) |
|
 | 儉儉儉丅恀媡側梊尵偱偡偗偳丄偦偺崻嫆偼?? | |
 |
Descartes偼丄\(\theta_1>\theta_2\)偵側傞偺偼丄悈拞偱岝偵壗傜偐偺椡偑摥偄偨偐傜偵堘偄側偄偲峫偊偨偺偱偡丅
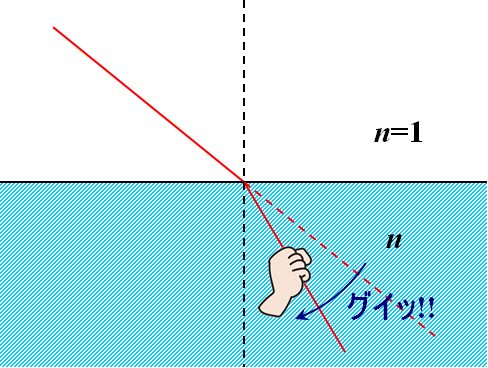 恾1.8.14 Descartes偺峫嶡 椡偑摥偗偽丄Newton曽掱幃偐傜壛懍搙偑惗偠傑偡偐傜丄懍搙偼懍偔側傝傑偡傛偹?? |
|
 | 傫乣丅偦傟偼偦傟偱丄愢摼椡偁傝傑偡偹丅 | |
 | 恾1.8.14偼丄岝傪棻巕偲峫偊傞偲忋庤偔愢柧偱偒偦偆偱偡丅傛偭偰丄Descartes偼棻巕愢偺僗僞儞僗偩偲尵偊傑偡丅 | |
 | 攈敶栤戣偩丅 | |
 | 巆擮側偑傜丄摉帪偺媄弍偱偙偺梊尵傪捈愙揑偵妋偐傔傞偙偲偼偱偒傑偣傫偱偟偨偑丄栺200擭屻丄偙偺幚尡揑徹柧偵挧愴偟惉岟偟偨恖偑偄傑偡丅 | |
 | 扤偱偡偐?? | |
 | 岝懍傪崅惛搙偱媮傔偨Foucault偱偡傛丅 | |
 | 偍乣丅嵞搊応偩丅 | |
 | Foucault偼丄岝懍傪媮傔偨偺偲摨偠夞揮儈儔乕偺幚尡憰抲傪巊偄丄岝楬偺拞偵悈憛傪愝抲偡傞偙偲偱丄朷墦嬀偵旘傃崬傫偱偒偨岝偺偢傟検偑丄悈憛偑側偄偲偒偲斾妑偟偰戝偒偄偙偲傪妋擣偡傞偺偱偡丅 | |
 | Fermat傕丄憪梩偺堿偐傜婌傫偱傑偡偹丅 | |
 | 岝偺棻巕愢丄攇摦愢偺榖偼丄偪傚偙偪傚偙弌偰偒傑偡偺偱丄偦偺偲偒偵嵞傃怗傟偨偄偲巚偄傑偡丅 |
| 慜暸傊 | 栠傞 | 師暸傊 |