 | 前回、連続の条件を導出しました。 | |
 |
この4つですね。 連続条件ⅰ)電場の接線成分は異なる媒質の前後において連続である 連続条件ⅱ)磁場の接線成分は異なる媒質の前後において連続である 連続条件ⅲ)磁束密度の法線成分は異なる媒質の前後において連続である 連続条件ⅳ)電束密度の法線成分は異なる媒質の前後において連続である |
|
 |
そこで、図2.2.1を、偏光を考慮して書き直します。
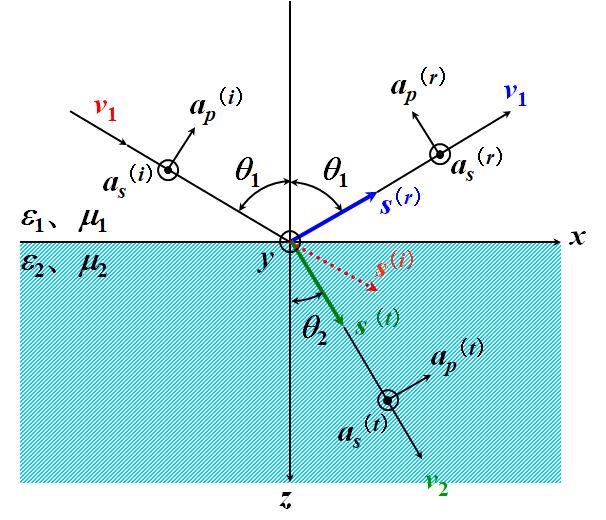 図2.2.4 Fresnel係数の導出 |
|
 | ん??\(p\)と\(s\)?? | |
 | 入射光・反射光・屈折光のいずれも偏光は任意です。しかし、どのような偏光であっても、必ず2つの直交する直線偏光に分解できるので、入射平面に垂直な成分と、入射平面に平行で光の進む向きに垂直な成分に分けました。\(p\)は後者の成分で、入射平面に平行だからparallelの頭文字を使ってます。\(s\)は前者の成分で、垂直を意味するドイツ語senkrechtの頭文字を使っているのです(\(a\)は振幅)。 | |
 | 英語だとperpendicularで同じ\(p\)を使うことになるからドイツ語か…。 | |
 | まず、電場の\(p\)成分について考えましょう。連続条件ⅰから、 \[ {a_p}^{\left( i \right)} \cos \theta_1 - {a_p}^{\left( r \right)} \cos \theta_1 = {a_p}^{\left( t \right)} \cos \theta_2 \tag{2.2.21} \] が成立します。 | |
 | はい。 | |
 | さて、電場の\(p\)成分に対応する磁場は\(s\)成分になる、というのはいいですか?? | |
 | 光の電場と磁場は直交するからですか?? | |
 | そうです。そして、その振幅には式1.11.8の関係がありました。よって、式1.11.9のアドミタンスYを使えば、連続条件ⅱは、 \[ Y_1 {a_p}^{\left( i \right)} + Y_1 {a_p}^{\left( r \right)} = Y_2 {a_p}^{\left( t \right)} \tag{2.2.22} \] と書くことができます。 | |
 | これで、電場の\(p\)偏光と、磁場の\(s\)偏光の関係式が出たわけですね。 | |
 | 今度は電場の\(s\)成分です。 | |
 | 連続条件ⅰから、 \[ {a_s}^{\left( i \right)} + {a_s}^{\left( r \right)} = {a_s}^{\left( t \right)} \tag{2.2.23} \] ですね。 | |
 | では、磁場成分については?? | |
 | ん~と。 \[ Y_1 {a_s}^{\left( i \right)} \cos \theta_1 - Y_1 {a_s}^{\left( r \right)} \cos \theta_1 = Y_2 {a_s}^{\left( t \right)} \cos \theta_2 \tag{2.2.24} \] かな。 | |
 | これで、電場の\(s\)偏光と、磁場の\(p\)偏光の関係式が出たことになります。では、式2.2.21と式2.2.22を使って、\({a_p}^{\left(t\right)}\)を消去してください。 | |
 | 式2.2.21に\(Y_2\)を掛けて、式2.2.22に\(\cos\theta_2\)を掛けて―。 \[ Y_2 {a_p}^{\left( i \right)} \cos \theta_1 - Y_2 {a_p}^{\left( r \right)} \cos \theta_1 = Y_2 {a_p}^{\left( t \right)} \cos \theta_2 \] \[ Y_1 {a_p}^{\left( i \right)} \cos \theta_2 + Y_1 {a_p}^{\left( r \right)} \cos \theta_2 = Y_2 {a_p}^{\left( t \right)} \cos \theta_2 \] 両辺を引けば―。 \[ \left( Y_2 \cos \theta_1 - Y_1 \cos \theta_2 \right) {a_p}^{\left( i \right)} - \left( Y_2 \cos \theta_1 + Y_1 \cos \theta_2 \right) {a_p}^{\left( r \right)} = 0 \] \[ \Leftrightarrow \quad \frac{ {a_p}^{\left( r \right)} }{ {a_p}^{\left( i \right)} } = \frac{ Y_2 \cos \theta_1 - Y_1 \cos \theta_2 }{ Y_2 \cos \theta_1 + Y_1 \cos \theta_2 } = \frac{ \sqrt{ \cfrac{\varepsilon_2}{\mu_2} } \cos \theta_1 - \sqrt{ \cfrac{\varepsilon_1}{\mu_1} } \cos \theta_2 }{ \sqrt{ \cfrac{\varepsilon_2}{\mu_2} } \cos \theta_1 + \sqrt{ \cfrac{\varepsilon_1}{\mu_1} } \cos \theta_2 } \] | |
 | \(\mu_1\fallingdotseq\mu_2\)ですし、式1.8.5が使えそうですよね。 | |
 | そっか。 \[ \frac{ {a_p}^{\left( r \right)} }{ {a_p}^{\left( i \right)} } \approx \frac{ \sqrt{ \varepsilon_2 } \cos \theta_1 - \sqrt{ \varepsilon_1 } \cos \theta_2 }{ \sqrt{ \varepsilon_2 } \cos \theta_1 + \sqrt{ \varepsilon_1 } \cos \theta_2 } \approx \frac{ n_2 \cos \theta_1 - n_1 \cos \theta_2 }{ n_2 \cos \theta_1 + n_1 \cos \theta_2 } \tag{2.2.25} \] | |
 | 更に、次のSnellの法則が成立します。 \[ n_1 \sin \theta_1 = n_2 \sin \theta_2 \tag{2.2.26} \] | |
 | そうすると、 \[ \frac{ {a_p}^{\left( r \right)} }{ {a_p}^{\left( i \right)} } = \frac{ \cfrac{n_2}{n_1} \cos \theta_1 - \cos \theta_2 }{ \cfrac{n_2}{n_1} \cos \theta_1 + \cos \theta_2 } = \frac{ \cfrac{\sin \theta_1}{\sin \theta_2} \cos \theta_1 - \cos \theta_2 }{ \cfrac{\sin \theta_1}{\sin \theta_2} \cos \theta_1 + \cos \theta_2 } \] \[ \phantom{\frac{ {a_p}^{\left( r \right)} }{ {a_p}^{\left( i \right)} }} = \frac{ \sin \theta_1 \cos \theta_1 - \sin \theta_2 \cos \theta_2 }{ \sin \theta_1 \cos \theta_1 + \sin \theta_2 \cos \theta_2 } \] | |
 | 右辺は、もうちょっと整理できそうですね。 | |
 | え??本当?? | |
 | まず、分子から見ていくと、 \[ \sin \theta_1 \cos \theta_1 - \sin \theta_2 \cos \theta_2 \\ = \sin \theta_1 \cos \theta_1 \left( \cos^2 \theta_2 + \sin^2 \theta_2 \right) - \sin \theta_2 \cos \theta_2 \left( \cos^2 \theta_1 + \sin^2 \theta_1 \right) \\ = \sin \theta_1 \cos \theta_1 \cos^2 \theta_2 + \sin \theta_1 \cos \theta_1 \sin^2 \theta_2 \\ \quad \quad \quad \quad \quad \quad - \sin \theta_2 \cos \theta_2 \cos^2 \theta_1 - \sin \theta_2 \cos \theta_2 \sin^2 \theta_1 \\ = \sin \theta_1 \cos \theta_2 \cos \theta_1 \cos \theta_2 + \sin \theta_2 \cos \theta_1 \sin \theta_1 \sin \theta_2 \\ \quad \quad \quad \quad \quad \quad - \sin \theta_2 \cos \theta_1 \cos \theta_1 \cos \theta_2 - \sin \theta_1 \cos \theta_2 \sin \theta_1 \sin \theta_2 \\ = \sin \theta_1 \cos \theta_2 \left( \cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 \right) \\ \quad \quad \quad \quad \quad \quad - \sin \theta_2 \cos \theta_1 \left( \cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 \right) \\ = \left( \sin \theta_1 \cos \theta_2 - \sin \theta_2 \cos \theta_1 \right) \left( \cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 \right) \] \[ = \sin \left( \theta_1 - \theta_2 \right) \cos \left( \theta_1 + \theta_2 \right) \tag{2.2.27} \] ですし、分母は、 \[ \sin \theta_1 \cos \theta_1 + \sin \theta_2 \cos \theta_2 \\ = \sin \theta_1 \cos \theta_1 \left( \cos^2 \theta_2 + \sin^2 \theta_2 \right) + \sin \theta_2 \cos \theta_2 \left( \cos^2 \theta_1 + \sin^2 \theta_1 \right) \\ = \sin \theta_1 \cos \theta_1 \cos^2 \theta_2 + \sin \theta_1 \cos \theta_1 \sin^2 \theta_2 \\ \quad \quad \quad \quad \quad \quad + \sin \theta_2 \cos \theta_2 \cos^2 \theta_1 + \sin \theta_2 \cos \theta_2 \sin^2 \theta_1 \\ = \sin \theta_1 \cos \theta_2 \cos \theta_1 \cos \theta_2 + \sin \theta_2 \cos \theta_1 \sin \theta_1 \sin \theta_2 \\ \quad \quad \quad \quad \quad \quad + \sin \theta_2 \cos \theta_1 \cos \theta_1 \cos \theta_2 + \sin \theta_1 \cos \theta_2 \sin \theta_1 \sin \theta_2 \\ = \sin \theta_1 \cos \theta_2 \left( \cos \theta_1 \cos \theta_2 + \sin \theta_1 \sin \theta_2 \right) \\ \quad \quad \quad \quad \quad \quad + \sin \theta_2 \cos \theta_1 \left( \cos \theta_1 \cos \theta_2 + \sin \theta_1 \sin \theta_2 \right) \\ = \left( \sin \theta_1 \cos \theta_2 + \sin \theta_2 \cos \theta_1 \right) \left( \cos \theta_1 \cos \theta_2 + \sin \theta_1 \sin \theta_2 \right) \] \[ = \sin \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 - \theta_2 \right) \tag{2.2.28} \] ですよね。 | |
 | そうすると―。 \[ \frac{ {a_p}^{\left( r \right)} }{ {a_p}^{\left( i \right)} } = \frac{ \sin \left( \theta_1 - \theta_2 \right) \cos \left( \theta_1 + \theta_2 \right) }{ \sin \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 - \theta_2 \right) } = \frac{ \tan \left( \theta_1 - \theta_2 \right) }{ \tan \left( \theta_1 + \theta_2 \right) } \] だ。 | |
 | 左辺は、\(p\)偏光の振幅反射率\(r_p\)と定義しましょう。従って、 \[ r_p \equiv \frac{ {a_p}^{\left( r \right)} }{ {a_p}^{\left( i \right)} } = \frac{ \tan \left( \theta_1 - \theta_2 \right) }{ \tan \left( \theta_1 + \theta_2 \right) } \tag{2.2.29} \] が導けたことになります。次は、式2.2.21と式2.2.22を使って、\({a_p}^{\left(r\right)}\)を消去してください。 | |
 | 式2.2.21に\(Y_1\)を掛けて、式2.2.22に\(\cos\theta_1\)を掛けて―。 \[ Y_1 {a_p}^{\left( i \right)} \cos \theta_1 - Y_1 {a_p}^{\left( r \right)} \cos \theta_1 = Y_1 {a_p}^{\left( t \right)} \cos \theta_2 \] \[ Y_1 {a_p}^{\left( i \right)} \cos \theta_1 + Y_1 {a_p}^{\left( r \right)} \cos \theta_1 = Y_2 {a_p}^{\left( t \right)} \cos \theta_1 \] 両辺を足せば―。 \[ 2 Y_1 {a_p}^{\left( i \right)} \cos \theta_1 = \left( Y_1 \cos \theta_2 + Y_2 \cos \theta_1 \right) {a_p}^{\left( t \right)} \] \[ \Leftrightarrow \quad \frac{ {a_p}^{\left( t \right)} }{ {a_p}^{\left( i \right)} } = \frac{ 2 Y_1 \cos \theta_1 }{ Y_1 \cos \theta_2 + Y_2 \cos \theta_1 } = \frac{ 2 \sqrt{ \cfrac{\varepsilon_1}{\mu_1} } \cos \theta_1 }{ \sqrt{ \cfrac{\varepsilon_1}{\mu_1} } \cos \theta_2 + \sqrt{ \cfrac{\varepsilon_2}{\mu_2} } \cos \theta_1 } \] \[ \phantom{\Leftrightarrow \quad \frac{ {a_p}^{\left( t \right)} }{ {a_p}^{\left( i \right)} }} \approx \frac{ 2 \sqrt{ \varepsilon_1 } \cos \theta_1 }{ \sqrt{ \varepsilon_1 } \cos \theta_2 + \sqrt{ \varepsilon_2 } \cos \theta_1 } \approx \frac{ 2 n_1 \cos \theta_1 }{ n_1 \cos \theta_2 + n_2 \cos \theta_1 } \tag{2.2.30} \] で、式2.2.26が成立するから―、 \[ \begin{align*} \frac{ {a_p}^{\left( t \right)} }{ {a_p}^{\left( i \right)} } &= \frac{ 2 \cos \theta_1 }{ \cos \theta_2 + \cfrac{n_2}{n_1} \cos \theta_1 } = \frac{ 2 \cos \theta_1 }{ \cos \theta_2 + \cfrac{\sin \theta_1}{\sin \theta_2} \cos \theta_1 } \\ &= \frac{ 2 \sin \theta_2 \cos \theta_1 }{ \sin \theta_2 \cos \theta_2 + \sin \theta_1 \cos \theta_1 } \end{align*} \] | |
 | 左辺は、\(p\)偏光の振幅透過率\(t_p\)と定義しましょう。また、右辺の分母は式2.2.28が使えそうです。 \[ t_p \equiv \frac{ {a_s}^{\left( t \right)} }{ {a_s}^{\left( i \right)} } = \frac{ 2 \sin \theta_2 \cos \theta_1 }{ \sin \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 - \theta_2 \right) } \tag{2.2.31} \] 今度は、式2.2.23と式2.2.24を使って、\({a_s}^{\left(t\right)}\)を消去してください。 | |
 | 式2.2.23に\(Y_2 \cos\theta_2\)を掛けて、 \[ Y_2 {a_s}^{\left( i \right)} \cos \theta_2 + Y_2 {a_s}^{\left( r \right)} \cos \theta_2 = Y_2 {a_s}^{\left( t \right)} \cos \theta_2 \] \[ Y_1 {a_s}^{\left( i \right)} \cos \theta_1 - Y_1 {a_s}^{\left( r \right)} \cos \theta_1 = Y_2 {a_s}^{\left( t \right)} \cos \theta_2 \tag{2.2.24} \] 両辺を引けば―。 \[ \left( Y_1 \cos \theta_1 - Y_2 \cos \theta_2 \right) {a_s}^{\left( i \right)} - \left( Y_1 \cos \theta_1 + Y_2 \cos \theta_2 \right) {a_s}^{\left( r \right)} = 0 \] \[ \Leftrightarrow \quad \frac{ {a_s}^{\left( r \right)} }{ {a_s}^{\left( i \right)} } = \frac{ Y_1 \cos \theta_1 - Y_2 \cos \theta_2 }{ Y_1 \cos \theta_1 + Y_2 \cos \theta_2 } = \frac{ \sqrt{\cfrac{\varepsilon_1}{\mu_1}} \cos \theta_1 - \sqrt{\cfrac{\varepsilon_2}{\mu_2}} \cos \theta_2 }{ \sqrt{\cfrac{\varepsilon_1}{\mu_1}} \cos \theta_1 + \sqrt{\cfrac{\varepsilon_2}{\mu_2}} \cos \theta_2 } \\ \] \[ \phantom{\Leftrightarrow \quad \frac{ {a_s}^{\left( r \right)} }{ {a_s}^{\left( i \right)} }} \approx \frac{ \sqrt{\varepsilon_1} \cos \theta_1 - \sqrt{\varepsilon_2} \cos \theta_2 }{ \sqrt{\varepsilon_1} \cos \theta_1 + \sqrt{\varepsilon_2} \cos \theta_2 } \approx \frac{ n_1 \cos \theta_1 - n_2 \cos \theta_2 }{ n_1 \cos \theta_1 + n_2 \cos \theta_2 } \tag{2.2.32} \] で、式2.2.26が成立するから―、 \[ \begin{align*} \frac{ {a_s}^{\left( r \right)} }{ {a_s}^{\left( i \right)} } &= \frac{ \cos \theta_1 - \cfrac{n_2}{n_1} \cos \theta_2 }{ \cos \theta_1 + \cfrac{n_2}{n_1} \cos \theta_2 } = \frac{ \cos \theta_1 - \cfrac{\sin \theta_1}{\sin \theta_2} \cos \theta_2 }{ \cos \theta_1 + \cfrac{\sin \theta_1}{\sin \theta_2} \cos \theta_2 } \\ &= \frac{ \sin \theta_2 \cos \theta_1 - \sin \theta_1 \cos \theta_2 }{ \sin \theta_2 \cos \theta_1 + \sin \theta_1 \cos \theta_2 } = -\frac{ \sin \left( \theta_1 - \theta_2 \right) }{ \sin \left( \theta_1 + \theta_2 \right) } \end{align*} \] | |
 | 左辺は、\(s\)偏光の振幅反射率\(r_s\)と定義しましょう。 \[ r_s \equiv \frac{ {a_s}^{\left( r \right)} }{ {a_s}^{\left( i \right)} } = -\frac{ \sin \left( \theta_1 - \theta_2 \right) }{ \sin \left( \theta_1 + \theta_2 \right) } \tag{2.2.33} \] 最後に、式2.2.23と式2.2.24を使って、\({a_s}^{\left(r\right)}\)を消去してください。 | |
 | 式2.2.23に\(Y_1\cos\theta_1\)を掛けて―。 \[ Y_1 {a_s}^{\left( i \right)} \cos \theta_1 + Y_1 {a_s}^{\left( r \right)} \cos \theta_1 = Y_1 {a_s}^{\left( t \right)} \cos \theta_1 \] \[ Y_1 {a_s}^{\left( i \right)} \cos \theta_1 - Y_1 {a_s}^{\left( r \right)} \cos \theta_1 = Y_2 {a_s}^{\left( t \right)} \cos \theta_2 \tag{2.2.24} \] 両辺を足せば―。 \[ 2 Y_1 {a_s}^{\left( i \right)} \cos \theta_1 = \left( Y_1 \cos \theta_1 + Y_2 \cos \theta_2 \right) {a_s}^{\left( t \right)} \] \[ \Leftrightarrow \quad \frac{ {a_s}^{\left( t \right)} }{ {a_s}^{\left( i \right)} } = \frac{ 2 Y_1 \cos \theta_1 }{ Y_1 \cos \theta_1 + Y_2 \cos \theta_2 } = \frac{ 2 \sqrt{ \cfrac{\varepsilon_1}{\mu_1} } \cos \theta_1 }{ \sqrt{ \cfrac{\varepsilon_1}{\mu_1} } \cos \theta_1 + \sqrt{ \cfrac{\varepsilon_2}{\mu_2} } \cos \theta_2 } \\ \] \[ \phantom{\Leftrightarrow \quad \frac{ {a_s}^{\left( t \right)} }{ {a_s}^{\left( i \right)} }} \approx \frac{ 2 \sqrt{ \varepsilon_1 } \cos \theta_1 }{ \sqrt{ \varepsilon_1 } \cos \theta_1 + \sqrt{ \varepsilon_2 } \cos \theta_2 } \approx \frac{ 2 n_1 \cos \theta_1 }{ n_1 \cos \theta_1 + n_2 \cos \theta_2 } \tag{2.2.34} \] で、式2.2.26が成立するから―、 \[ \begin{align*} \frac{ {a_s}^{\left( t \right)} }{ {a_s}^{\left( i \right)} } &= \frac{ 2 \cos \theta_1 }{ \cos \theta_1 + \cfrac{n_2}{n_1} \cos \theta_2 } = \frac{ 2 \cos \theta_1 }{ \cos \theta_1 + \cfrac{\sin \theta_1}{\sin \theta_2} \cos \theta_2 } \\ &= \frac{ 2 \sin \theta_2 \cos \theta_1 }{ \sin \theta_2 \cos \theta_1 + \sin \theta_1 \cos \theta_2 } = \frac{ 2 \sin \theta_2 \cos \theta_1 }{ \sin \left( \theta_1 + \theta_2 \right) } \end{align*} \] | |
 |
左辺は、\(s\)偏光の振幅透過率\(t_s\)と定義しましょう。
\[
t_s \equiv \frac{ {a_s}^{\left( t \right)} }{ {a_s}^{\left( i \right)} } = \frac{ 2 \sin \theta_2 \cos \theta_1 }{ \sin \left( \theta_1 + \theta_2 \right) } \tag{2.2.35}
\]
以上で、入射光の振幅が、反射光と屈折光にどう分配されるかが導出されました(論文)。この4つの式をFresnel係数と言います。
 Augustin Jean Fresnel(1788~1827) |
|
 | この人、何か冴えない顔してますね…。 | |
 | そう…ですか…ね。実際、Fresnelは他の多くの物理学者と違って、8歳になっても読み書きできなかったとか、青年期まではあまりパッとしない人物だったようです。 | |
 | お、そういう人もいるんだ。 | |
 | 時代的にNapolèon政権後のゴタゴタした動乱期と重なっていて、こういう政治的に不安定な状況だと青年はたいてい政治運動に加担するんですが、Fresnelもご多分に漏れず、そのせいで一時期、牢獄にぶち込まれます。 | |
 | ただのチンピラ…。 | |
 | しかし、その暗い部屋の格子窓から漏れる光を見ながら、光学の理論を構築していったと言われているんですよ。 | |
 | それは意外…。教授。式2.2.29、式2.2.31、式2.2.33、式2.2.35のFresnel係数は、\(\theta_1=0\)の垂直入射だと計算できませんけど?? | |
 | その場合は、反射率なら式2.2.25、式2.2.32を、透過率なら式2.2.30、式2.2.34を使えばいいですよ。 | |
 | う~ん。透過率は、どっちで計算しても、 \[ t_p = t_s = \frac{ 2 n_1 }{ n_1 + n_2 } \tag{2.2.36} \] で分かるんですど、反射率は、 \[ r_p = -r_s = \frac{ n_2 - n_1 }{ n_2 + n_1 } \tag{2.2.37} \] で、\(p\)偏光と\(s\)偏光で符号が逆になるんですけど?? | |
 |
それは、ベクトルの向きを図2.2.4のように定義したからですね。例えば\(n_2>n_1\)だと、\(r_p>0\)、\(r_s<0\)ですが、これは図2.2.4の定義において、\({a_p}^{\left(r\right)}\)は変わらないけれども、\({a_s}^{\left(r\right)}\)は反対向きにしないといけない、ということを意味するのです。
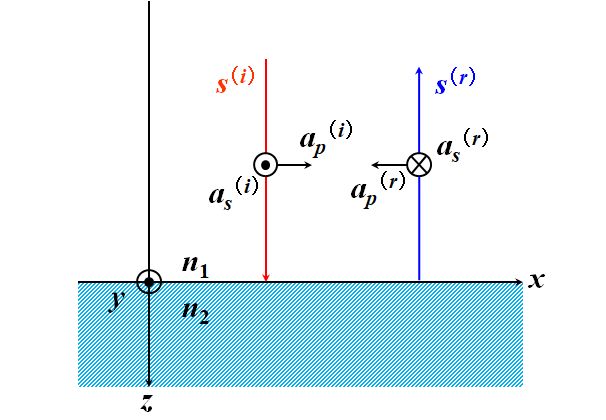 図2.2.5 固定端の反射 |
|
 | 何か、\(180^{\circ}\)回転したみたいに見えますね。 | |
 | 振幅\(a\)が\(A\mathrm{e}^{i\phi_0}\)だったことを思い出せば、反射波の振幅は入射波の振幅に\(-1=\mathrm{e}^{i\pi}\)を掛けたものになった、ということです。 | |
 | \(A\mathrm{e}^{i\phi_0}\)が\(A\mathrm{e}^{i\left(\phi_0+\pi\right)}\)に変わったってことですね。 | |
 | つまり、屈折率の大きい媒質に入射した光の反射光は\(\pi\)の位相変化を受けるということなのです。 | |
 | あ~、ひょっとして固定端とかいうやつ?? | |
 |
そうです。一方、\(n_2 < n_1\)だと、\(r_p < 0\)、\(r_s > 0\)ですが、これは図2.2.4の定義において、\({a_s}^{\left(r\right)}\)は変わらないけれども、\({a_p}^{\left(r\right)}\)は反対向きにしないといけない、ということを意味するのです。
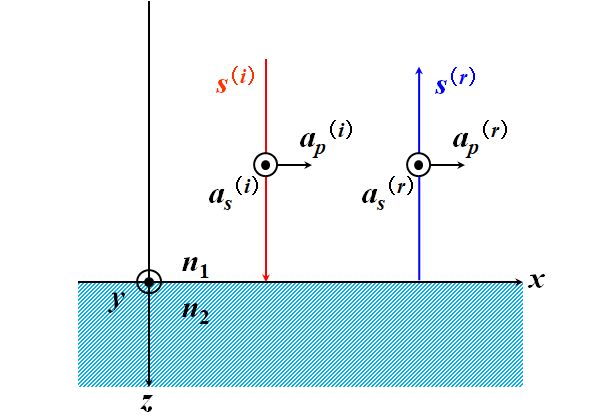 図2.2.6 自由端の反射 |
|
 | 何も変わらず、か。ということは、これは自由端ってことですね。 | |
 | 式2.2.37の符号の問題は、このように解釈するわけです。 |
| 前頁へ | 戻る | 次頁へ |