 | 波動光学から、従来より知られている反射の法則と屈折の法則を厳密に導くことができます。 | |
 | へぇ。そうなんだ。 | |
 | まず、平面波は式1.1.13で表されましたが、初期位相を振幅の中に含ませて、新しい振幅を改めて\(a\)と書きましょう。 \[ \begin{align*} u \big( \vec{\mathstrut r},t \big) &= A \exp \Big[ i \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \big) \Big] = A \mathrm{e}^{i \phi_0} \exp \Big[ i \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t \big) \Big] \\ &= a \exp \Big[ i \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t \big) \Big] \tag{2.2.1} \end{align*} \] 更に、式1.11.6を使って、括弧の中を\(\omega\)で括ってやります。 \[ u \big( \vec{\mathstrut r},t \big) = a \exp \bigg[ i \omega \Big( \frac{ \vec{\mathstrut s} \cdot \vec{\mathstrut r} }{ v } - t \Big) \bigg] \tag{2.2.2} \] \(\vec{\mathstrut s}\)は波数ベクトルの単位ベクトルです。 | |
 | はい。 | |
 |
そのうえで、図2.2.1のように入射を\(i\)、反射を\(r\)、屈折を\(t\)という添え字で表し、入射角、反射角、屈折角を\(\theta_1\)、\({\theta_1}^{\thinspace \prime}\)、\(\theta_2\)と置きます。
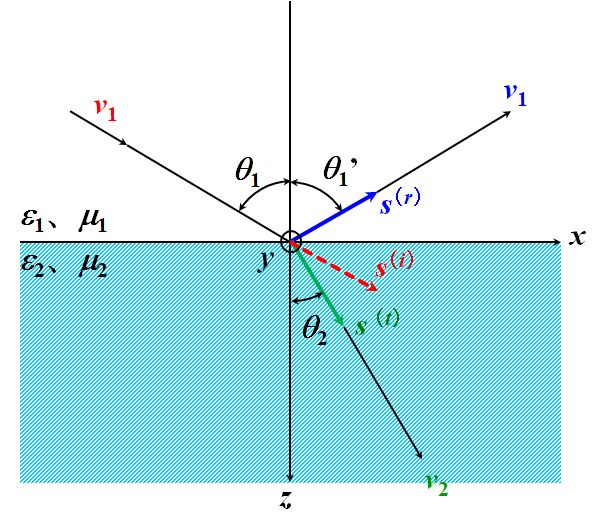 図2.2.1 反射の法則と屈折の法則の導出 |
|
 | 入射角と反射角は同じですけど?? | |
 | それは、今は知らないという体で進めます。 | |
 | ふ~ん。 | |
 | 境界面における、それぞれの平面波を式で表してください。 | |
 | 境界面ということは\(z=0\)ってことか…。 \[ u^{\left( i \right)} \big( \vec{\mathstrut r},t \big) = a^{\left( i \right)} \exp \left[ i \omega \left( \frac{ {s_x}^{\left( i \right)} x + {s_y}^{\left( i \right)} y }{ v_1 } - t \right) \right] \tag{2.2.3} \] \[ u^{\left( r \right)} \big( \vec{\mathstrut r},t \big) = a^{\left( r \right)} \exp \left[ i \omega \left( \frac{ {s_x}^{\left( r \right)} x + {s_y}^{\left( r \right)} y }{ v_1 } - t \right) \right] \tag{2.2.4} \] \[ u^{\left( t \right)} \big( \vec{\mathstrut r},t \big) = a^{\left( t \right)} \exp \left[ i \omega \left( \frac{ {s_x}^{\left( t \right)} x + {s_y}^{\left( t \right)} y }{ v_2 } - t \right) \right] \tag{2.2.5} \] | |
 | 境界面では位相が整合してないといけないと言いましたよね?? | |
 | あぁ、そうでしたね。つまり、 \[ \frac{ {s_x}^{\left( i \right)} x + {s_y}^{\left( i \right)} y }{ v_1 } - t = \frac{ {s_x}^{\left( r \right)} x + {s_y}^{\left( r \right)} y }{ v_1 } - t = \frac{ {s_x}^{\left( t \right)} x + {s_y}^{\left( t \right)} y }{ v_2 } - t \tag{2.2.6} \] ってこと?? | |
 | OKです。式2.2.6がすべての\(x\)、\(y\)で成立するためには、どうなってないといけないですか?? | |
 | すべてか…。そうすると、 \[ \frac{ {s_x}^{\left( i \right)} }{ v_1 } = \frac{ {s_x}^{\left( r \right)} }{ v_1 } = \frac{ {s_x}^{\left( t \right)} }{ v_2 } \tag{2.2.7} \] \[ \frac{ {s_y}^{\left( i \right)} }{ v_1 } = \frac{ {s_y}^{\left( r \right)} }{ v_1 } = \frac{ {s_y}^{\left( t \right)} }{ v_2 } \tag{2.2.8} \] が同時に成立しないとダメそうです。 | |
 | 入射波が\(xz\)平面内に存在するならば、\({s_y}^{\left(i\right)}=0\)としてもいいですよね?? | |
 | あれ??そうすると、式2.2.8から、\({s_y}^{\left(r\right)}={s_y}^{\left(t\right)}=0\)ですね。 | |
 | \(xz\)平面は、入射波の\(\vec{\mathstrut s^{\left(i\right)}}\)と、境界面の法線によって張られる面と言い換えてもよく、それを入射平面と呼びますが、式2.2.8から導かれた結論は、反射波も屈折波も、入射波と同じ入射平面に存在するということを意味します。 | |
 | なるほど。 | |
 | 次に、式2.2.7の1つ目の等号から、 \[ \frac{ {s_x}^{\left( i \right)} }{ v_1 } = \frac{ {s_x}^{\left( r \right)} }{ v_1 } \quad \Leftrightarrow \quad {s_x}^{\left( i \right)} = {s_x}^{\left( r \right)} \] ですが、\({s_x}^{\left(i\right)}=\sin\theta_1\)、\({s_x}^{\left(r\right)}=\sin{\theta_1}^{\thinspace \prime}\)なので、 \[ \sin \theta_1 = \sin {\theta_1}^{\thinspace \prime} \quad \Leftrightarrow \quad \theta_1 = {\theta_1}^{\thinspace \prime} \tag{2.2.9} \] という反射の法則が導かれました。 | |
 | そうすると、式2.2.7の2つ目の等号から、 \[ \begin{align*} &\frac{ {s_x}^{\left( i \right)} }{ v_1 } = \frac{ {s_x}^{\left( t \right)} }{ v_2 } \quad \Leftrightarrow \quad \frac{ {s_x}^{\left( i \right)} }{ {s_x}^{\left( t \right)} } = \frac{ v_1 }{ v_2 } \\ &\Leftrightarrow \quad \frac{ \sin \theta_1 }{ \sin \theta_2 } = \frac{ v_1 }{ v_2 } = \sqrt{ \frac{ \varepsilon_2 \mu_2 }{ \varepsilon_1 \mu_1 } } = \frac{ n_2 }{ n_1 } \tag{2.2.10} \end{align*} \] となって、Snellの法則が導かれるわけですね。 |
~連続の条件~
 | さて。次に繋げるための準備を、ここでしておきましょう。 | |
 | 準備?? | |
 | はい。ただ、以下に示す内容は、結果だけ受け入れれば次に繋がるので、計算の苦手な人は飛ばしても構いません。 | |
 | つまり、数学なわけですね…。 | |
 |
まず、図2.2.2のように、境界面の両側に跨るように極めて小さい経路\(C\)(P1P2Q2Q1)を考えます。
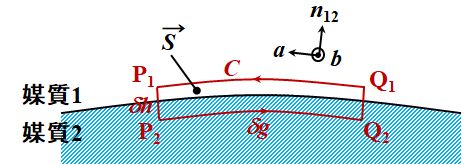 図2.2.2 連続の条件(1) |
|
 | その経路のとり方は?? | |
 | P1Q1及びP2Q2は境界面に平行で、P1P2及びQ1Q2は境界面に垂直です。 | |
 | ふむ。 | |
 | ここで、式1.4.2を、経路\(C\)で囲まれた領域\(S\)で面積分します(\(d\vec{\mathstrut s}\)は面要素で、紙面に垂直なベクトルとする)。 \[ \iint_S \nabla \times \vec{\mathstrut E} \cdot d\vec{\mathstrut s} = - \iint_S \frac{ \partial \vec{\mathstrut B} }{ \partial t } \cdot d\vec{\mathstrut s} = -\frac{ \partial }{ \partial t } \iint_S \vec{\mathstrut B} \cdot d\vec{\mathstrut s} \tag{2.2.11} \] 左辺はStokesの定理が適用できますね?? | |
 | 面積分が線積分に変換できるってやつ?? | |
 | そうです。つまり(\(d\vec{\mathstrut l}\)は線要素)、 \[ \iint_S \nabla \times \vec{\mathstrut E} \cdot d\vec{\mathstrut s} = \oint_C \vec{\mathstrut E} \cdot d\vec{\mathstrut l} = -\frac{ \partial }{ \partial t } \iint_S \vec{\mathstrut B} \cdot d\vec{\mathstrut s} \tag{2.2.12} \] また、\(\overline{{\rm P}_1{\rm Q}_1}=\overline{{\rm P}_2{\rm Q}_2}=\delta g\)、\(\overline{{\rm P}_1{\rm P}_2}=\overline{{\rm Q}_1{\rm Q}_2}=\delta h\)とすると、式2.2.12は、 \[ \vec{\mathstrut E_1} \cdot \vec{\mathstrut a} \delta g - \vec{\mathstrut E_2} \cdot \vec{\mathstrut a} \delta g + C_{\rm edge} = - \frac{ \partial \vec{\mathstrut B} }{ \partial t} \cdot \vec{\mathstrut b} \delta g \delta h \tag{2.2.13} \] となります。 | |
 | ムムム。\(\vec{\mathstrut E_1}\)は媒質1の電場、\(\vec{\mathstrut E_2}\)は媒質2の電場?? | |
 | はい。更に、\(\vec{\mathstrut a}\)は境界面に平行な単位ベクトル、\(\vec{\mathstrut b}\)は\(S\)の法線ベクトル(\(\vec{\mathstrut S}\))に平行な単位ベクトルです。 | |
 | \(C_{\rm edge}\)っていうのは?? | |
 | 経路\(C\)のうち、\(\overline{{\rm P}_1{\rm P}_2}\)と\(\overline{{\rm Q}_1{\rm Q}_2}\)の寄与分です。\(\delta h\rightarrow0\)の極限をとったら、どうせ消えちゃいますからね。 | |
 | ん??てことは、\(\delta h\rightarrow0\)の極限だと、 \[ \big( \vec{\mathstrut E_1} \cdot \vec{\mathstrut a} - \vec{\mathstrut E_2} \cdot \vec{\mathstrut a} \big) \delta g = 0 \tag{2.2.14} \] ですか?? | |
 | そうです。更に、\(\vec{\mathstrut a}=\vec{\mathstrut b}\times\vec{\mathstrut n_{12}}\)となるように、境界面に垂直なベクトル\(\vec{\mathstrut n_{12}}\)を考えると、式2.2.14は、 \[ \vec{\mathstrut b} \cdot \Big[ \vec{\mathstrut n_{12}} \times \big( \vec{\mathstrut E_1} - \vec{\mathstrut E_2} \big) \Big] = 0 \tag{2.2.15} \] と変形できます。しかも、\(\vec{\mathstrut b}\)は任意に選択できるので、 \[ \vec{\mathstrut n_{12}} \times \big( \vec{\mathstrut E_1} - \vec{\mathstrut E_2} \big) = 0 \tag{2.2.16} \] が成立しないといけません。 | |
 | う~ん。\(\vec{\mathstrut n_{12}}\)と外積した結果が\(0\)ってことは、\(\vec{\mathstrut E_1}\)とか\(\vec{\mathstrut E_2}\)は、電場の境界面に平行な成分ってことになるから…。 | |
 |
それを接線成分と呼ぶことにすると、 連続条件ⅰ)電場の接線成分は異なる媒質の前後において連続である ということになります。 |
|
 | そういうことか。あれ??ひょっとして、磁場についても同じことが言えませんか?? | |
 |
誘電体の場合は、電場と磁場が完全に対称なので、そうですね。すなわち、 連続条件ⅱ)磁場の接線成分は異なる媒質の前後において連続である も成立します。 |
|
 | 法線成分については、そういう連続性は成立しない?? | |
 |
成立しますが、ちょっと捻りが加わります。では、図2.2.3のように、境界面の両側に跨るように極めて薄い円筒\(V\)を考えましょう。
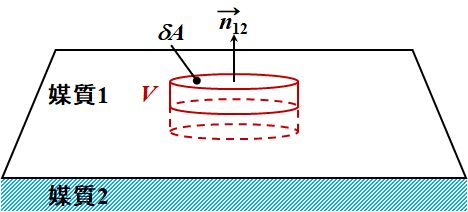 図2.2.3 連続の条件(2) |
|
 | 次は円筒かぁ。 | |
 | ここで、式1.4.4を体積分します(\(dV\)は体積要素)。 \[ \iiint_V \nabla \cdot \vec{\mathstrut B} dV = 0 \tag{2.2.17} \] 左辺はGaussの定理が適用できますね?? | |
 | 体積分が面積分に変換できるってやつ?? | |
 | そうです。つまり、 \[ \iiint_S \nabla \cdot \vec{\mathstrut B} dV = \iint_S \vec{\mathstrut B} \cdot d\vec{\mathstrut s} = 0 \tag{2.2.18} \] また、円筒の上面、下面の面積を\(\delta A\)とすると、 \[ \vec{\mathstrut B_1} \cdot \vec{\mathstrut n_{12}} \delta A - \vec{\mathstrut B_2} \cdot \vec{\mathstrut n_{12}} \delta A + C_{\rm side} = 0 \tag{2.2.19} \] となります。 | |
 | \(\vec{\mathstrut B_1}\)は媒質1の磁束密度、\(\vec{\mathstrut B_2}\)は媒質2の磁束密度、\(C_{\rm side}\)は側面の寄与ってことですね?? | |
 | そうです。ここで側面の高さを\(0\)に近づけると、 \[ \begin{align*} &\vec{\mathstrut B_1} \cdot \vec{\mathstrut n_{12}} \delta A - \vec{\mathstrut B_2} \cdot \vec{\mathstrut n_{12}} \delta A = 0 \\ &\Leftrightarrow \quad \big( \vec{\mathstrut B_1} - \vec{\mathstrut B_2} \big) \cdot \vec{\mathstrut n_{12}} = 0 \tag{2.2.20} \end{align*} \] | |
 | う~ん。\(\vec{\mathstrut n_{12}}\)と内積した結果が\(0\)ってことは、\(\vec{\mathstrut B_1}\)とか\(\vec{\mathstrut B_2}\)は、磁束密度の境界面に垂直な成分ってことになるから…。 | |
 |
それを法線成分と呼ぶことにすると、 連続条件ⅲ)磁束密度の法線成分は異なる媒質の前後において連続である ということになります。 |
|
 | で、それは電束密度も同じだ、と。 | |
 |
誘電体の場合という制限つきですが、 連続条件ⅳ)電束密度の法線成分は異なる媒質の前後において連続である も成立します。 |
|
 | これで、すべての連続の条件が出たわけですね?? | |
 | そうです。これを使って、次回はFresnel係数を導出します。 | |
 | 今回は予告つきだ…。 |
| 前頁へ | 戻る | 次頁へ |