 |
繰り返しになりますが、偏光は、式2.1.22と式2.1.23のように直交する2つの直線偏光に分解することができます。
\[
E_x = A_x \exp \big[ i \left( kz - \omega t + \phi_x \right) \big] \tag{2.1.22}
\]
\[
E_y = A_y \exp \big[ i \left( kz - \omega t + \phi_x + \delta \right) \big] \tag{2.1.23}
\]
この光が、\(x\)方向から\(\theta\)だけ傾いた透過軸を持つ直線偏光子を透過したときの強度\(I(\theta)\)を求めてみましょう。
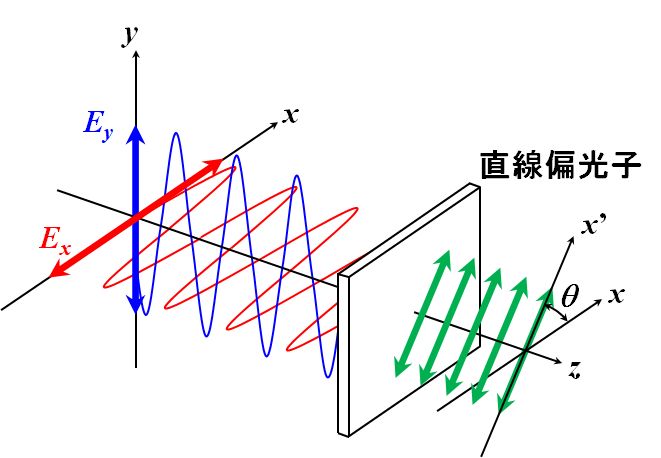 図2.1.5 強度\(I(\theta)\)を求める |
|
 | 座標変換が必要ですよね?? | |
 | そうですね。それは、 \[ \left( \begin{array}{c} E_{x^{\thinspace \prime}} \\ E_{y^{\thinspace \prime}} \end{array} \right) = \left( \begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array} \right) \left( \begin{array}{c} E_x \\ E_y \end{array} \right) = \left( \begin{array}{c} E_x \cos \theta + E_y \sin \theta \\ -E_x \sin \theta + E_y \cos \theta \end{array} \right) \] で計算できます。 | |
 | \(x^{\thinspace \prime}\)方向しか通過しないから、その成分を2乗すれば強度が計算できる、ってことでいいんでしたっけ?? | |
 | はい。 | |
 | 何か大変そうだなぁ。 \[ \begin{align*} I \left( \theta \right) &= \left| E_{x^{\thinspace \prime}} \right|^2 \\ &= \left| E_x \right|^2 \cos^2 \theta + E_x {E_y}^{*} \sin \theta \cos \theta + {E_x}^{*} E_y \sin \theta \cos \theta + \left| E_y \right|^2 \sin^2 \theta \\ &= {A_x}^2 \cos^2 \theta + A_x A_y \mathrm{e}^{-i \delta} \sin \theta \cos \theta + A_x A_y \mathrm{e}^{i \delta} \sin \theta \cos \theta + {A_y}^2 \sin^2 \theta \\ &= {A_x}^2 \frac{ 1 + \cos 2 \theta }{ 2 } + A_x A_y \left( \mathrm{e}^{i \delta} + \mathrm{e}^{-i \delta} \right) \sin \theta \cos \theta + {A_y}^2 \frac{ 1 - \cos 2 \theta }{ 2 } \\ &= \frac{ {A_x}^2 + {A_y}^2 }{ 2 } + \frac{ {A_x}^2 - {A_y}^2 }{ 2 } \cos 2 \theta + 2 A_x A_y \cos \delta \sin \theta \cos \theta \\ &= \frac{ {A_x}^2 + {A_y}^2 }{ 2 } + \frac{ {A_x}^2 - {A_y}^2 }{ 2 } \cos 2 \theta + A_x A_y \sin 2 \theta \cos \delta \end{align*} \] ですね。 | |
 | では、\(\theta=0^{\circ}\)、\(45^{\circ}\)、\(90^{\circ}\)、\(135^{\circ}\)のときの強度は、それぞれどうなりますか?? | |
 | \(\theta=0^{\circ}\)だと、 \[ I \left( 0^{\circ} \right) = {A_x}^2 \tag{2.1.24} \] \(\theta=90^{\circ}\)だと、 \[ I \left( 90^{\circ} \right) = {A_y}^2 \tag{2.1.25} \] \(\theta=45^{\circ}\)だと、 \[ I \left( 45^{\circ} \right) = \frac{ {A_x}^2 + {A_y}^2 }{ 2 } + A_x A_y \cos \delta \tag{2.1.26} \] \(\theta=135^{\circ}\)だと、 \[ I \left( 135^{\circ} \right) = \frac{ {A_x}^2 + {A_y}^2 }{ 2 } - A_x A_y \cos \delta \tag{2.1.27} \] です。 | |
 |
次に、\(\theta=45^{\circ}\)の直線偏光子の前に、進相軸を\(x\)方向に設定した1/4波長板を設置することを考えます。
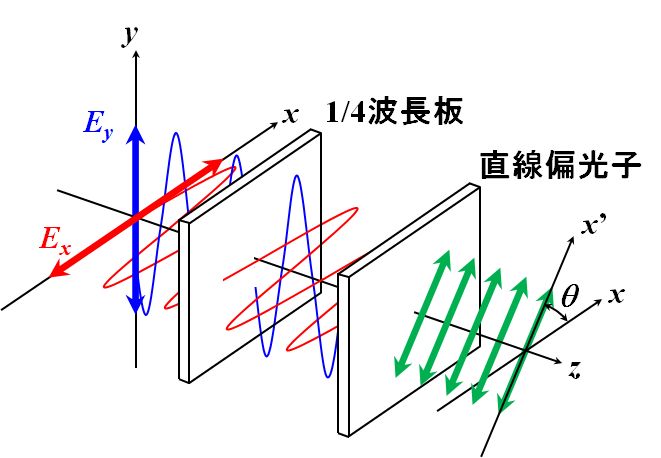 図2.1.6 強度\(I_L(\theta)\)を求める 式2.1.26はどう書き換えられるでしょう?? |
|
 | 1/4波長板は、\(x\)方向の位相を\(\cfrac{\pi}{2}\)だけ進めるんでしたっけ?? | |
 | そうです。言い方を変えると、\(y\)方向の位相を\(\cfrac{\pi}{2}\)だけ遅らせます。 | |
 | だったら、式2.1.26の\(\delta\)を\(\delta-\cfrac{\pi}{2}\)に置き換えればよさそうですね。 \[ I_L \left( 45^{\circ} \right) = \frac{ {A_x}^2 + {A_y}^2 }{ 2 } + A_x A_y \cos \left( \delta - \frac{ \pi }{ 2 } \right) = \frac{ {A_x}^2 + {A_y}^2 }{ 2 } + A_x A_y \sin \delta \tag{2.1.28} \] | |
 | では、\(\theta=135^{\circ}\)の直線偏光子の前に、同じように1/4波長板を設置したら、式2.1.27はどう書き換えられるでしょう?? | |
 | 式2.1.27の\(\delta\)を\(\delta-\cfrac{\pi}{2}\)に置き換えるだけだから、 \[ I_L \left( 135^{\circ} \right) = \frac{ {A_x}^2 + {A_y}^2 }{ 2 } - A_x A_y \cos \left( \delta - \frac{ \pi }{ 2 } \right) = \frac{ {A_x}^2 + {A_y}^2 }{ 2 } - A_x A_y \sin \delta \tag{2.1.29} \] | |
 | というわけで、6つの強度が求まりました。これらはすべて、計測可能な量ですね?? | |
 | そうですね。 | |
 |
そこで、次のようなパラメータを定義します。
\[
s_0 = I \left( 0^{\circ} \right) + I \left( 90^{\circ} \right) = {A_x}^2 + {A_y}^2 \tag{2.1.30}
\]
\[
s_1 = I \left( 0^{\circ} \right) - I \left( 90^{\circ} \right) = {A_x}^2 - {A_y}^2 \tag{2.1.31}
\]
\[
s_2 = I \left( 45^{\circ} \right) - I \left( 135^{\circ} \right) = 2 A_x A_y \cos \delta \tag{2.1.32}
\]
\[
s_3 = I_L \left( 45^{\circ} \right) - I_L \left( 135^{\circ} \right) = 2 A_x A_y \sin \delta \tag{2.1.33}
\]
これらをStokesパラメータと言います。
 Sir George Gabriel Stokes(1819~1903) |
|
 | また、新しい定義が導入されましたね。 | |
 | Stokesは、この6つの強度を測定すれば、偏光を知るのに必要な\(A_x\)、\(A_y\)、\(\delta\)が求まると主張した(論文)のです。 | |
 | ムムム。言われてみれば、そうですね…。\(\delta\)は式2.1.32で式2.1.33を割れば出せるのか。 \[ \frac{ s_3 }{ s_2 } = \tan \delta \quad \Leftrightarrow \quad \delta = \tan^{-1} \left( \frac{ s_3 }{ s_2 } \right) \tag{2.1.34} \] | |
 | 偏光を実際に知ろうとすると意外と難しいんですが、Stokesは1/4波長板を使うというアイデアで、その問題を解決したわけです。ちなみに、式2.1.30~2.1.33は、 \[ {s_0}^2 = {s_1}^2 + {s_2}^2 + {s_3}^2 \tag{2.1.35} \] を満たすことを確認しておいてください。 |
~Poincarè球~
 |
さて、光は一般的に楕円偏光していると言いました。
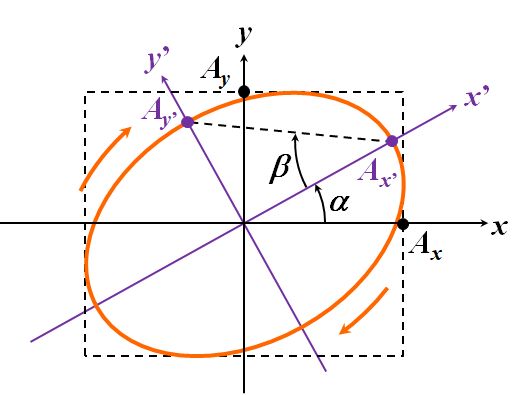 図2.1.7 楕円偏光分光計測 |
|
 | こうでしたっけね。 \[ \left( \frac{ E_x }{ A_x } \right)^2 - \frac{ 2 E_x E_y }{ A_x A_y } \cos \delta + \left( \frac{ E_y }{ A_y } \right)^2 = \sin^2 \delta \tag{2.1.5} \] | |
 | まず、式2.1.5で表される楕円が、\(x\)軸からどれだけ傾いているかを調べてみましょう。一般に、 \[ a x^2 + 2 b x y + c y^2 = d \tag{2.1.36} \] で表される楕円の傾き\(\alpha\)は、 \[ \tan 2 \alpha = \frac { 2 b }{ a - c } \tag{2.1.37} \] で計算できます。 | |
 | てことは、 \[ \tan 2 \alpha = -\frac { 2 \cos \delta }{ A_x A_y } \div \left( \frac{ 1 }{ {A_x}^2 }- \frac{ 1 }{ {A_y}^2 } \right) = \frac { 2 \cos \delta }{ A_x A_y } \times \frac{ {A_x}^2{A_y}^2 }{ {A_x}^2 - {A_y}^2 } = \frac { 2 A_x A_y \cos \delta }{ {A_x}^2 - {A_y}^2 } \] | |
 | Stokesパラメータを代入すると?? | |
 | ん~と。 \[ \tan 2 \alpha = \frac { s_2 }{ s_1 } \tag{2.1.38} \] かな。 | |
 | 次に、この楕円の長軸の長さの2乗と短軸の長さの2乗の比\({A_{x^{\thinspace \prime}}}^2 :{A_{y^{\thinspace \prime}}}^2\)を求めましょう。再び式2.1.36の楕円の場合、 \[ \left( \begin{array}{cc} a & b\\ b & c \end{array} \right) \] という行列の固有値を計算すれば、簡単に求めることができます。 | |
 | 簡単にって…。固有値の計算方法なんて忘れちゃいましたけど。 | |
 | しょうがないですね。行列\(F\)の固有値\(\Lambda\)は、単位行列\(E\)を使って、 \[ \mathrm{det} \left( F - \Lambda E \right) = 0 \] という方程式を解けばいいのです。 | |
 | これはこれで大変そうだなぁ。 \[ \left| \begin{array}{cc} \cfrac{ 1 }{ {A_x}^2 } - \Lambda & -\cfrac{ \cos \delta }{ A_x A_y } \\ -\cfrac{ \cos \delta }{ A_x A_y } & \cfrac{ 1 }{ {A_y}^2 } - \Lambda \end{array} \right| = \left( \frac{ 1 }{ {A_x}^2 } - \Lambda \right) \left( \frac{ 1 }{ {A_y}^2 } - \Lambda \right) - \frac{ \cos^2 \delta }{ {A_x}^2 {A_y}^2 } \] \[ \begin{align*} &\quad\quad\quad = \Lambda ^2 - \left( \frac{ 1 }{ {A_x}^2 } + \frac{ 1 }{ {A_y}^2 } \right) \Lambda + \frac{ 1 }{ {A_x}^2 {A_y}^2 } - \frac{ \cos^2 \delta }{ {A_x}^2 {A_y}^2 } \\ &\quad\quad\quad = \Lambda ^2 - \left( \frac{ 1 }{ {A_x}^2 } + \frac{ 1 }{ {A_y}^2 } \right) \Lambda + \frac{ \sin^2 \delta }{ {A_x}^2 {A_y}^2 } = 0 \tag{2.1.39} \end{align*} \] え~、この方程式、解かないとダメですか?? | |
 | いえ。ここで止めておきましょう。そしたら、図2.1.7の\(\beta\)という角度を使って、次のような計算をしておきます。 \[ \sin 2 \beta = 2 \sin \beta \cos \beta = 2 \frac{ A_{x^{\thinspace \prime}} }{ \sqrt{ {A_{x^{\thinspace \prime}}}^2 + {A_{y^{\thinspace \prime}}}^2 } } \frac{ A_{y^{\thinspace \prime}} }{ \sqrt{ {A_{x^{\thinspace \prime}}}^2 + {A_{y^{\thinspace \prime}}}^2 } } = \frac{ 2 A_{x^{\thinspace \prime}} A_{y^{\thinspace \prime}} }{ {A_{x^{\thinspace \prime}}}^2 + {A_{y^{\thinspace \prime}}}^2 } = \frac{ 2 \sqrt{ \Lambda_1 \Lambda_2 } }{ \Lambda_1 + \Lambda_2 } \] \(\Lambda_1\)と\(\Lambda_2\)は式2.1.39の解です。 | |
 | お。解と係数の関係式が使えそうですね。 \[ \Lambda_1 + \Lambda_2 = \frac{ 1 }{ {A_x}^2 } + \frac{ 1 }{ {A_y}^2 } \] \[ \Lambda_1 \Lambda_2 = \frac{ \sin^2 \delta }{ {A_x}^2 {A_y}^2 } \] だから、 \[ \sin 2 \beta = \frac{ 2 \sqrt{ \Lambda_1 \Lambda_2 } }{ \Lambda_1 + \Lambda_2 } = 2 \sqrt{ \frac{ \sin^2 \delta }{ {A_x}^2 {A_y}^2 } } \div \left( \frac{ 1 }{ {A_x}^2 } + \frac{ 1 }{ {A_y}^2 } \right) = 2 \frac{ \sin \delta }{ A_x A_y } \times \frac{ {A_x}^2 {A_y}^2 }{ {A_x}^2 + {A_y}^2 } \] \[ \phantom{\sin 2 \beta}= \frac{ 2 A_x A_y \sin \delta } { {A_x}^2 + {A_y}^2 } = \frac{ s_3 } { s_0 } \tag{2.1.40} \] ですね。 | |
 | では、式2.1.38と式2.1.40を式2.1.35に代入してください。 | |
 | 今回は計算が多いなぁ…。 \[ {s_0}^2 = {s_1}^2 + \left( s_1 \tan 2 \alpha \right)^2 + \left( s_0 \sin 2 \beta \right)^2 \quad \Leftrightarrow \quad {s_0}^2 \left( 1 - \sin^2 2 \beta \right) = {s_1}^2 \left( 1 + \tan^2 2 \alpha \right) \] \[ \Leftrightarrow \quad {s_0}^2 \cos^2 2 \beta = {s_1}^2 \frac{ 1 }{ \cos^2 2 \alpha } \quad \Rightarrow \quad s_1 = s_0 \cos 2 \beta \cos 2 \alpha \tag{2.1.41} \] | |
 | そして、式2.1.41を式2.1.38に代入です。 | |
 | これで最後かな。 \[ s_2 = s_1 \tan 2 \alpha = s_0 \cos 2 \beta \cos 2 \alpha \tan 2 \alpha = s_0 \cos 2 \beta \sin 2 \alpha \tag{2.1.42} \] | |
 | 以上より、式2.1.31~2.1.33のStokesパラメータは、式2.1.40~式2.1.42に置き換え可能であることが示せました。 \[ s_1 = s_0 \cos 2 \beta \cos 2 \alpha \tag{2.1.41} \] \[ s_2 = s_0 \cos 2 \beta \sin 2 \alpha \tag{2.1.42} \] \[ s_3 = s_0 \sin 2 \beta \tag{2.1.40} \] | |
 | たくさん計算したわりには、結果はあっさりしてますね。でも、これで何が分かるんですか?? | |
 |
実は、式2.1.41~式2.1.43は、お互いに直交した\(s_1\)軸、\(s_2\)軸、\(s_3\)軸を持つ空間における、極座標\((s_0,2\alpha,2\beta)\)を示しているのです。
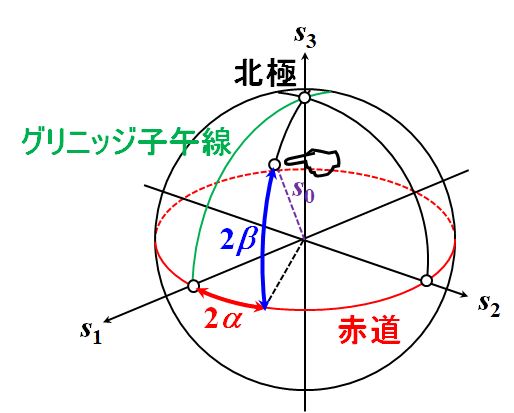 図2.1.8 Poincarè球 つまり、強度が\(s_0\)である光の偏光は、すべてこの球面上の1点に対応している、ということなんですよ。 |
|
 | う~ん。ピンと来ないですけど…。 | |
 |
例えば、北極は\((s_0,0^{\circ},90^{\circ})\)ですが、このとき\(\alpha=0^{\circ}\)、\(\beta=45^{\circ}\)なので、偏光は図2.1.9のようになっているわけです。
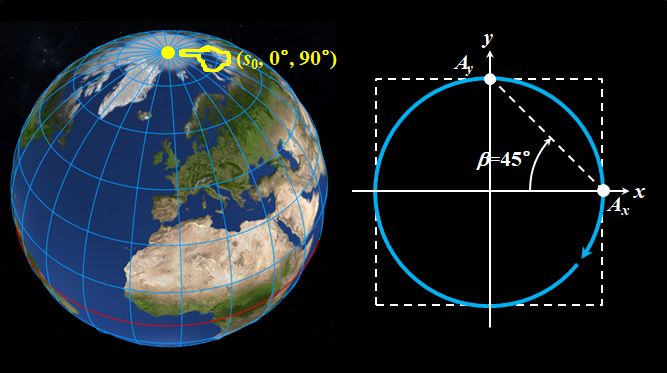 図2.1.9 北極\((0^{\circ},90^{\circ})\)の偏光 |
|
 | つまり、右まわり円偏光ってこと?? | |
 |
そうです。反対の南極は\((s_0,0^{\circ},-90^{\circ})\)なので、\(\alpha=0^{\circ}\)、\(\beta=-45^{\circ}\)となり、偏光は図2.1.10のようになっています。
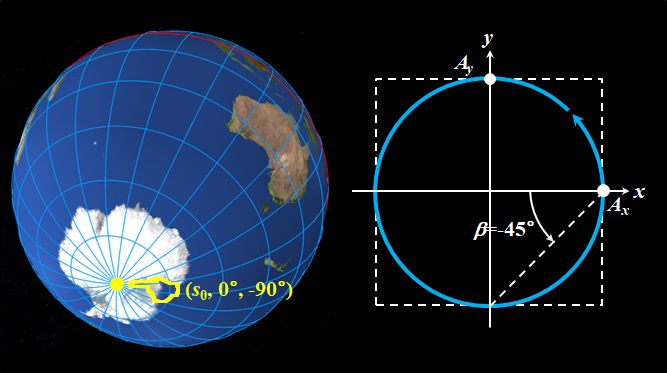 図2.1.10 南極\((0^{\circ},-90^{\circ})\)の偏光 |
|
 |
お、左まわり円偏光だ。そうすると、グリニッジ子午線と赤道の交点は\((s_0,0^{\circ},0^{\circ})\)だから、\(\alpha=\beta=0^{\circ}\)で、\(x\)方向の直線偏光ってことかぁ。
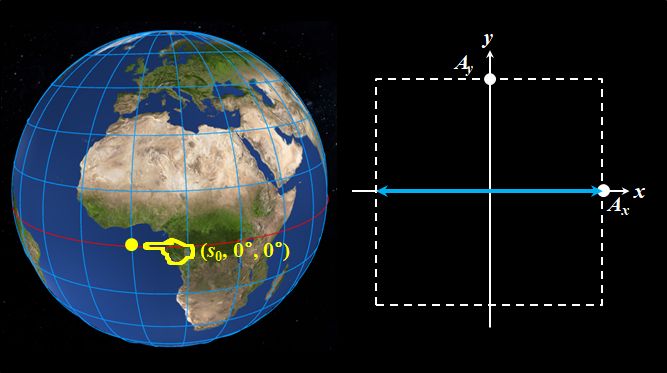 図2.1.11 \((0^{\circ},0^{\circ})\)の偏光 東経\(180^{\circ}\)と赤道の交点は\((s_0,180^{\circ},0^{\circ})\)だから、\(\alpha=90^{\circ}\)、\(\beta=0^{\circ}\)で、\(y\)方向の直線偏光になりますね。 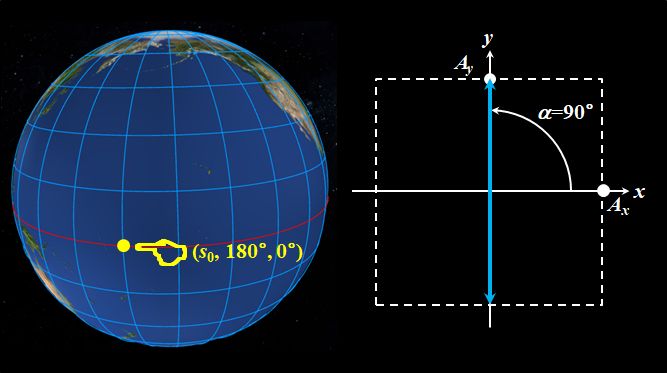 図2.1.12 \((180^{\circ},0^{\circ})\)の偏光 |
|
 | インドネシア共和国あたりはどうですか??東経\(90^{\circ}\)と赤道の交点付近ですけど。 | |
 |
\((s_0,90^{\circ},0^{\circ})\)だから、\(\alpha=45^{\circ}\)、\(\beta=0^{\circ}\)で、\(x\)方向から\(45^{\circ}\)傾いた直線偏光ですね。
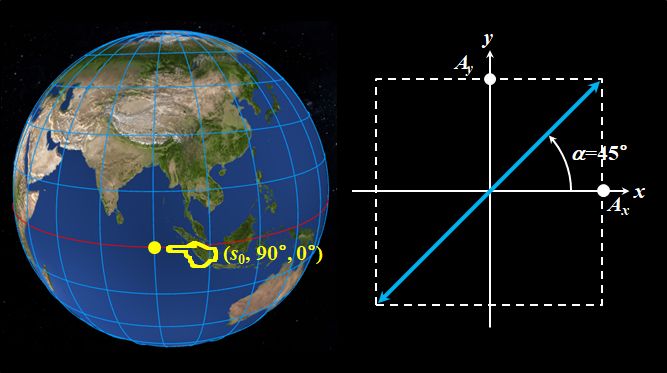 図2.1.13 \((90^{\circ},0^{\circ})\)の偏光 |
|
 |
つまり、赤道上はすべて直線偏光で、グリニッジ子午線からグルっと1周する間に、\(x\)方向の直線偏光(東経\(0^{\circ}\))→\(x\)方向から\(45^{\circ}\)傾いた直線偏光(東経\(90^{\circ}\))→\(y\)方向の直線偏光(東経\(180^{\circ}\))→\(x\)方向から\(-45^{\circ}\)傾いた直線偏光(西経\(90^{\circ}\))というように、偏光の方向がグルグルと1回転することになります。
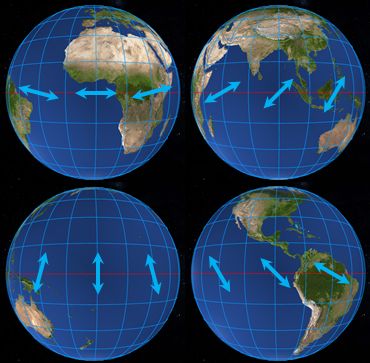 図2.1.14 赤道上の偏光の変化 |
|
 |
じゃぁ、グリニッジ子午線と北緯\(45^{\circ}\)の交点だと―。\((s_0,0^{\circ},45^{\circ})\)だから、\(\alpha=0^{\circ}\)、\(\beta=22.5^{\circ}\)で、右まわり楕円偏光ですね。
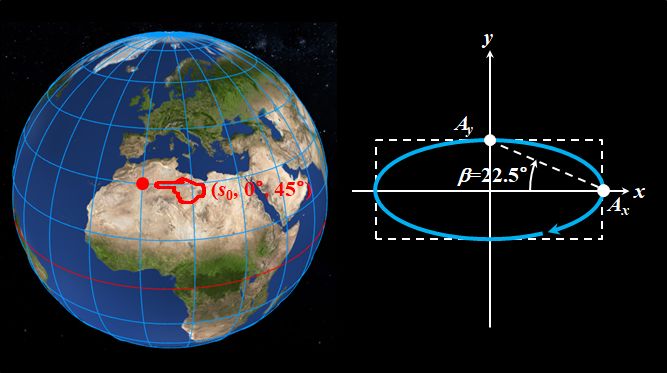 図2.1.15 \((0^{\circ},45^{\circ})\)の偏光 東経\(180^{\circ}\)と北緯\(45^{\circ}\)の交点だと―。\((s_0,180^{\circ},45^{\circ})\)だから、\(\alpha=90^{\circ}\)、\(\beta=22.5^{\circ}\)で、縦長の右まわり楕円偏光かぁ。 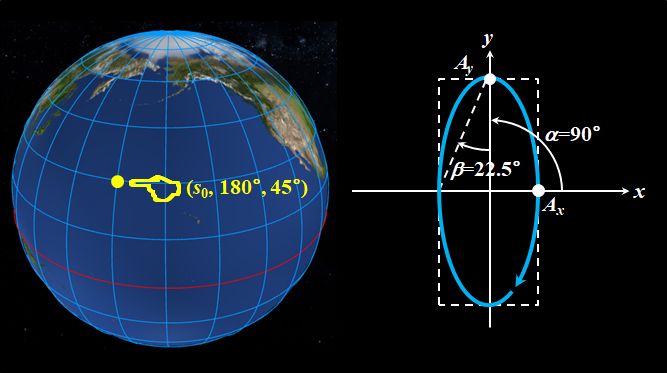 図2.1.16 \((180^{\circ},45^{\circ})\)の偏光 |
|
 |
つまり、北半球はすべて右まわりに相当し、南半球はすべて左まわりに相当するわけです。
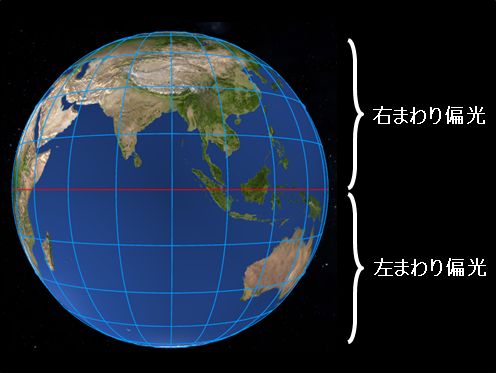 図2.1.17 北半球と南半球の偏光 |
|
 | 東京都庁だと?? | |
 | 東経\(140^{\circ}\)、北緯\(36^{\circ}\)ってところじゃないですかね?? | |
 |
\((s_0,140^{\circ},36^{\circ})\)だから、\(\alpha=70^{\circ}\)、\(\beta=18^{\circ}\)で、傾いた右まわり楕円偏光ですね。
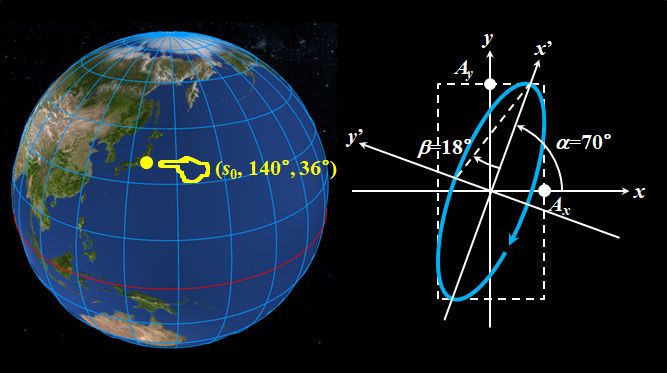 図2.1.18 \((140^{\circ},36^{\circ})\)の偏光 |
|
 |
同じ経線の上にあれば、それは傾き\(\alpha\)が同じということを意味するので、赤道から北極に向かって、傾きをキープしたまま直線偏光→楕円偏光→円偏光というイメージになります。
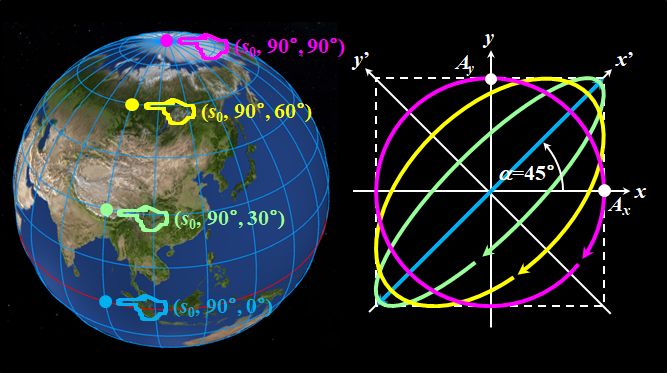 図2.1.19 同一経線上の偏光の変化 |
|
 | なるほど~。 | |
 | ここまでの議論は、\(\alpha\)と\(\beta\)が分かっているとして、極座標系から偏光を求めましたが、強度の測定で分かるのはStokesパラメータのみです。ということは、プロットできるのはDescartes座標系における点\((s_1,s_2,s_3)\)になります。しかし、その点が極座標系のどこに対応するかは一目瞭然なので、測定対象となっている光がどのような偏光かは、直ちに理解できるということなんですよ。 | |
 | そうか。測定結果から直感的に偏光が分かるってことなんですね。 | |
 | この方法の凄いのは、それだけではありません。ルールを覚えると、移相子によって偏光がどう変わるか、作図的に理解できます。 | |
 | え~、それは知りたいです。 |
~Jones計算法との関係~
 |
\(x\)方向から進相軸が\(\theta\)だけ傾いた、位相を\(\varepsilon\)だけ進める移相子の場合、ルールは次のとおりです。 ①\(\theta\)と一致する赤道上のポイントを探せ ②そのポイントが正面中央に来るように設定せよ ③入射光の偏光をプロットせよ ④プロットした地点から、\(\varepsilon\)に相当する角度だけ右まわりに旅をせよ |
|
 | それだけ?? | |
 | これだけです。具体的にやってみましょう(図2.1.20)。Jones計算法のときに、進相軸を\(x\)方向に設定した1/4波長板について検討しましたね?? | |
 |
やりましたね。 \(x\)方向に\(45^{\circ}\)傾いた直線偏光の入射光は、左まわり円偏光に変換される 左まわり円偏光の入射光は、\(x\)方向に\(-45^{\circ}\)傾いた直線偏光に変換される \(x\)方向に\(-45^{\circ}\)傾いた直線偏光の入射光は、右まわり円偏光に変換される 右まわり円偏光の入射光は、\(x\)方向に\(45^{\circ}\)傾いた直線偏光に変換される でした。 |
|
 |
まず、進相軸は\(0^{\circ}\)ですから、グリニッジ子午線と赤道の交点が正面中央に来るように設定します(a)。そして、\(x\)方向に\(45^{\circ}\)傾いた直線偏光の入射光の場合は、東経\(90^{\circ}\)と赤道の交点ですから、そこにプロットです(b)。更に、1/4波長板は\(\varepsilon=\cfrac{\pi}{2}=90^{\circ}\)ですから、\(90^{\circ}\)だけ右まわりに旅をするのです(c)。
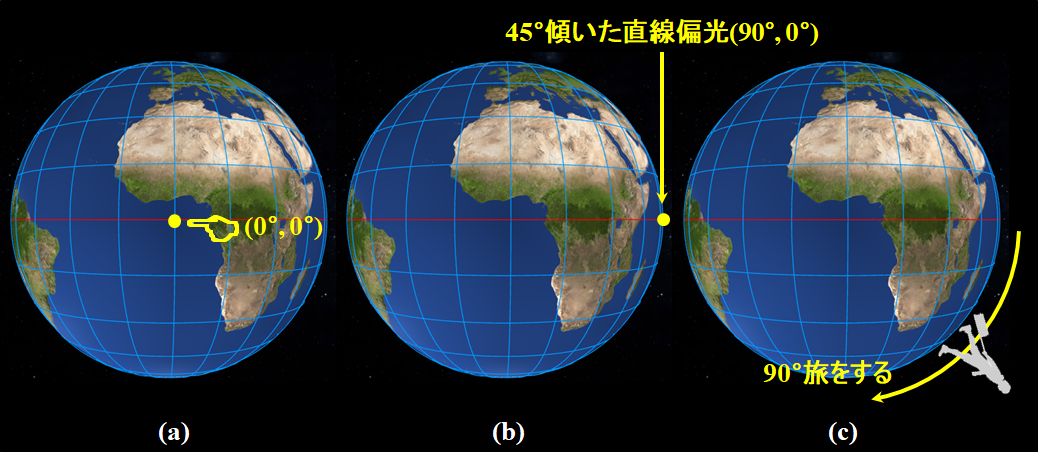 図2.1.20 1/4波長板による偏光の変化(1) |
|
 | そうすると、着地点は南極だから左まわり円偏光―。あ、Jones計算法と一致してる!! | |
 | はい。ルールさえ覚えてしまえば、Jones計算法など知らなくても、偏光がどう変わるか一発で分かります。 | |
 |
お~。これ、凄い。じゃぁ、同じ1/4波長板で、グリニッジ子午線と北緯\(45^{\circ}\)の交点の偏光を入射させると、東経\(45^{\circ}\)と赤道の交点の偏光に変換されるわけですね??
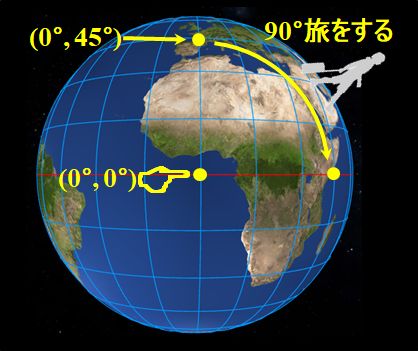 図2.1.21 1/4波長板による偏光の変化(2) |
|
 |
そうです。つまり、\(\alpha=22.5^{\circ}\)の直線偏光ですね。
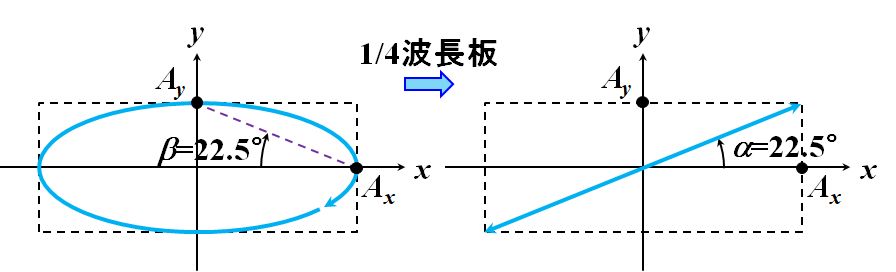 図2.1.22 1/4波長板による偏光の変化(3) Jones計算法でもそうなるか、計算してみてください。 |
|
 | 式2.1.41と式2.1.42から、\(s_2=0\)、\(s_3=\cfrac{1}{\sqrt{2}}\)だから、式2.1.34を使って\(\delta=90^{\circ}\)ですね。そうすると、Jonesベクトルは、 \[ \left( \begin{array}{c} E_x \\ E_y \end{array} \right) = \frac{ 1 }{ \sqrt{ {A_x}^2 + {A_y}^2 } } \left( \begin{array}{c} A_x \\ A_y \mathrm{e}^{i 90^{\circ} } \end{array} \right) \] だから、 \[ \left( \begin{array}{cc} 1 & 0\\ 0 & \mathrm{e}^{-i 90^{\circ} } \end{array} \right) \frac{ 1 }{ \sqrt{ {A_x}^2 + {A_y}^2 } } \left( \begin{array}{c} A_x \\ A_y \mathrm{e}^{i 90^{\circ} } \end{array} \right) = \frac{ 1 }{ \sqrt{ {A_x}^2 + {A_y}^2 } } \left( \begin{array}{c} A_x \\ A_y \end{array} \right) \] ってことは―?? | |
 | \(\delta=0\)なので、\((A_x,A_y)\)を通過する右肩上がりの直線偏光だってことですね。つまり、図2.1.22の右図になったわけです。 | |
 | Jones計算法だと、計算は面倒だし、考えること多いし、私はこっちの地球儀の方が好きだな~。 | |
 |
一応、地球儀は説明を分かりやすくする便宜的なもので、この球体は考案者の名前をとってPoincarè球と呼ばれています。
 Jules-Henri Poincarè(1854~1912) |
|
 | Poincarè予想の?? | |
 |
そうです。ドイツのHilbertと双璧をなす、数学のすべての分野に精通していた最後の数学者ですね。
 David Hilbert(1862~1943) |
|
 | それ以降はいない?? | |
 | 徹底的に細分化が進んでいきますからね。とても1人で網羅できる分量じゃないですよ。ちなみに、Poincarèは、Einsteinよりも早く特殊相対性理論を完成させていた(論文)とも言われています。 | |
 | 偏光については便利な道具が手に入ったので、とりあえずこれを使って理解を深めることにしま~す。 |
| 前頁へ | 戻る | 次頁へ |