 | さて、異方性媒質については一軸結晶と二軸結晶があるわけですが、ここでは比較的取り扱いの易しい一軸結晶に限定して議論しましょう。 | |
 | 比較的か…。 | |
 |
一軸結晶は2つの主屈折率が等しいので、それを\(n_x=n_y\)とします。
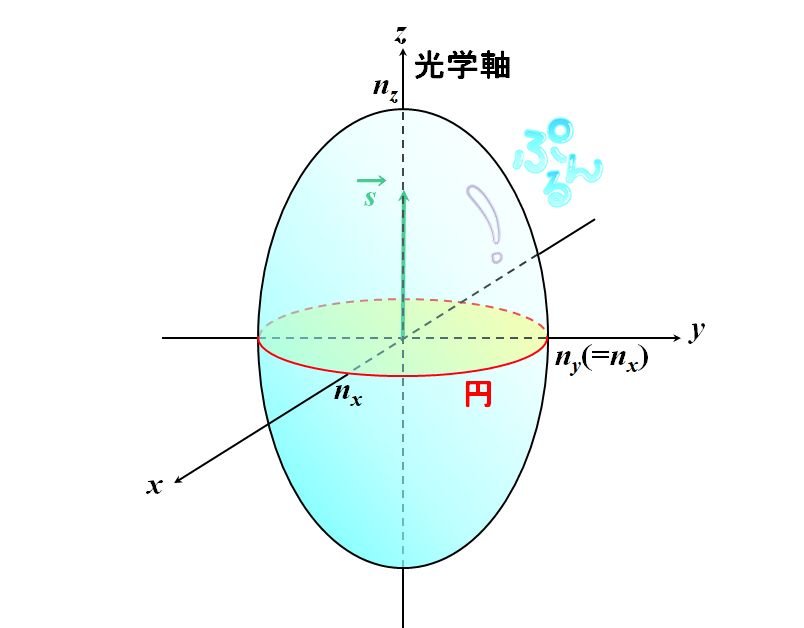 図2.8.1 一軸結晶の屈折率楕円体 このとき、波数ベクトルが\(z\)軸に一致していると、その断面は円になります。 |
|
 | そうすると、\(n^{\thinspace \prime}=n^{\thinspace \prime\prime}\)ですね。 | |
 | つまり、光はあたかも等方性媒質の結晶を伝搬しているように感じます。このように光が騙されてしまう結晶固有の軸のことを光学軸と言います。1軸結晶は、このような光学軸が1つしかありません。だから1軸結晶と言うのです。 | |
 | ということは、二軸結晶は光学軸が2つあるってこと?? | |
 |
そういうことですね。その確認は各自でやってみてください。また、一軸結晶の場合、波数ベクトルをどの向きに取ろうと、必ず一方の屈折率は\(n_x\)(\(=n_y\))になります。
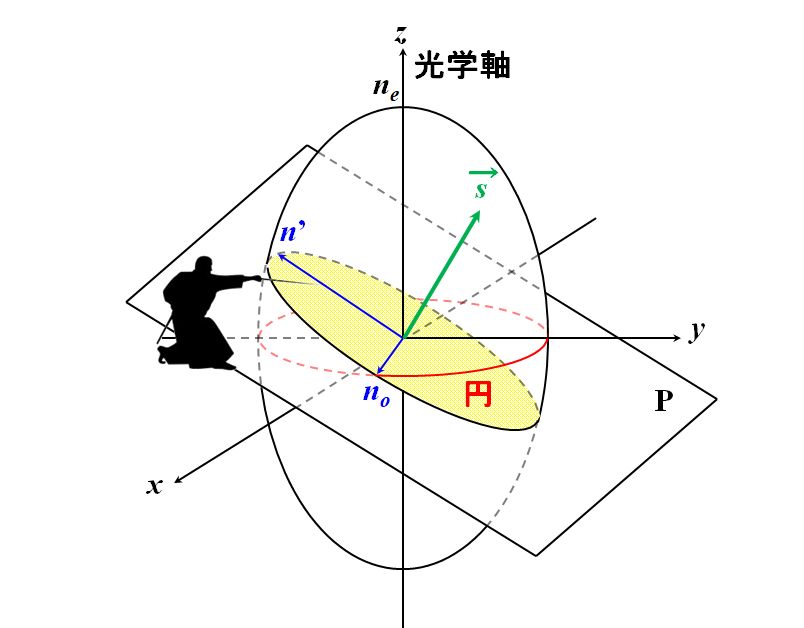 図2.8.2 一軸結晶の2つの屈折率 |
|
 | あ、確かに!! | |
 | ですので、これを常光線屈折率と呼ぶことにし、改めて\(n_o\)としましょう。\(o\)はordinaryの頭文字です。 | |
 | もう1つの屈折率は、入射する方向に依存して\(n_o\)から\(n_z\)まで変化するわけですね。 | |
 | そこで、\(n_z\)を改めて\(n_e\)と置き、異常光線屈折率と呼ぶことにします。 | |
 | extra-ordinaryの頭文字ってことか。 | |
 | \(n_o\)と\(n_e\)の大小関係に着目して、\(n_o < n_e\)のとき正の一軸結晶、\(n_o>n_e\)のとき負の一軸結晶と言うこともあります。 | |
 | 一軸結晶に入射した光は、\(n_o\)と、\(n_o\sim n_e\)までの屈折率\(n^{\thinspace \prime}\)の2つを感じるんでしょうけど、具体的な感じ方ってどうなっているんですか?? | |
 |
以前、どのような偏光であっても、必ず2つの直交する直線偏光に分解できると言いました。ですから、その分解方向を\(n_o\)と\(n^{\thinspace \prime}\)のそれぞれに合致するようにするのです。
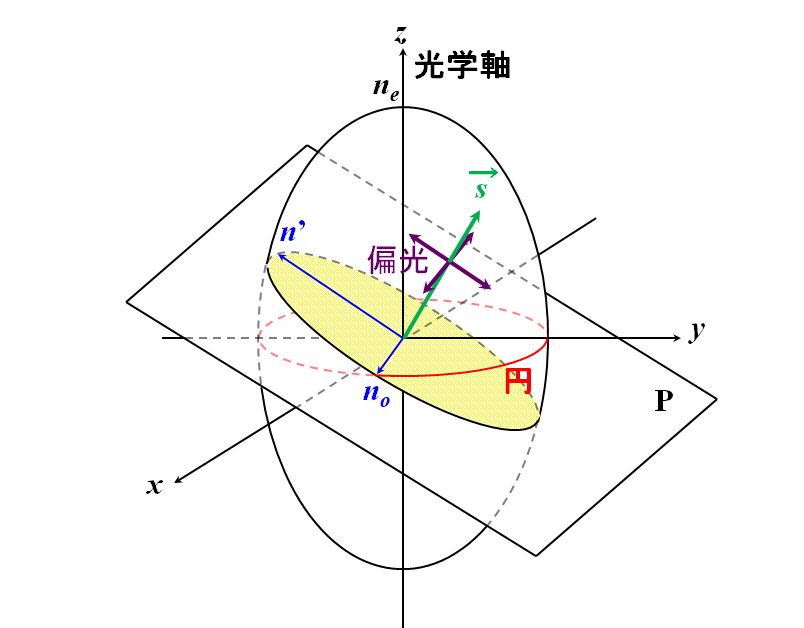 図2.8.3 分解された直線偏光と2つの屈折率の関係 それぞれの直線偏光が、対応する屈折率を感じながら伝搬することになります。 |
|
 | そういうことか。 | |
 | \(n_x=n_y=n_o\)、\(n_z=n_e\)として、Fresnel方程式を書き直してみましょう。 | |
 | そうすると―。 \[ \left( {n_o}^2 - n^2 \right) \left( {n_e}^2 - n^2 \right) {s_x}^2{n_o}^2 \\ \quad +\left( {n_e}^2 - n^2 \right) \left( {n_o}^2 - n^2 \right) {s_y}^2{n_o}^2 \\ \quad \quad +\left( {n_o}^2 - n^2 \right) \left( {n_o}^2 - n^2 \right) {s_z}^2{n_e}^2 \\ = \left( {n_o}^2 - n^2 \right) \big[ \left( {n_e}^2 - n^2 \right) {s_x}^2 {n_o}^2 + \left( {n_e}^2 - n^2 \right) {s_y}^2 {n_o}^2 + \left( {n_o}^2 - n^2 \right) {s_z}^2 {n_e}^2 \big] \\ = \left( {n_o}^2 - n^2 \right) \big[ {n_o}^2 {n_e}^2 \left( {s_x}^2 + {s_y}^2 + {s_z}^2 \right) - n^2 {n_o}^2 \left( {s_x}^2 + {s_y}^2 \right) - n^2 {n_e}^2 {s_z}^2 \big] \\ = \left( {n_o}^2 - n^2 \right) \big[ {n_o}^2 {n_e}^2 - n^2 {n_o}^2 \left( {s_x}^2 + {s_y}^2 \right) - n^2 {n_e}^2 {s_z}^2 \big] = 0 \] | |
 | ここから、 \[ n^2 = {n_o}^2 \tag{2.8.1} \] が導けますね。ま、当たり前の結果です。そして、もう1つの屈折率\(n^{\thinspace \prime}\)は、 \[ {n_o}^2 {n_e}^2 - n^2 {n_o}^2 \left( {s_x}^2 + {s_y}^2 \right) - n^2 {n_e}^2 {s_z}^2 = 0 \] \[ \Leftrightarrow \quad \frac{ {s_x}^2 + {s_y}^2 }{{n_e}^2} + \frac{ {s_z}^2 }{{n_o}^2} = \frac{1}{n^2} \tag{2.8.2} \] の解として与えられることが分かります。式2.8.1は見方によっては半径\(n_o\)の球面を表していると考えることもできますので、この屈折率に対応する偏光成分は、あたかも等方性媒質を伝搬しているように感じているはずです。よって、その振る舞いも、等方性媒質のときとまったく同じとなります。この成分の光は常光線と言いますね。 | |
 | ふむ。そうすると、それと直交する偏光成分の光は異常光線って言うわけですね。 | |
 |
では、どのくらい異常なのか調べてみましょう。まず、一軸結晶の場合、屈折率楕円体は光学軸(\(z\)軸)に対して回転対称だということに着目し、\(x\)軸と\(y\)軸を「波数ベクトルが\(xz\)平面内にある」ように設定します。
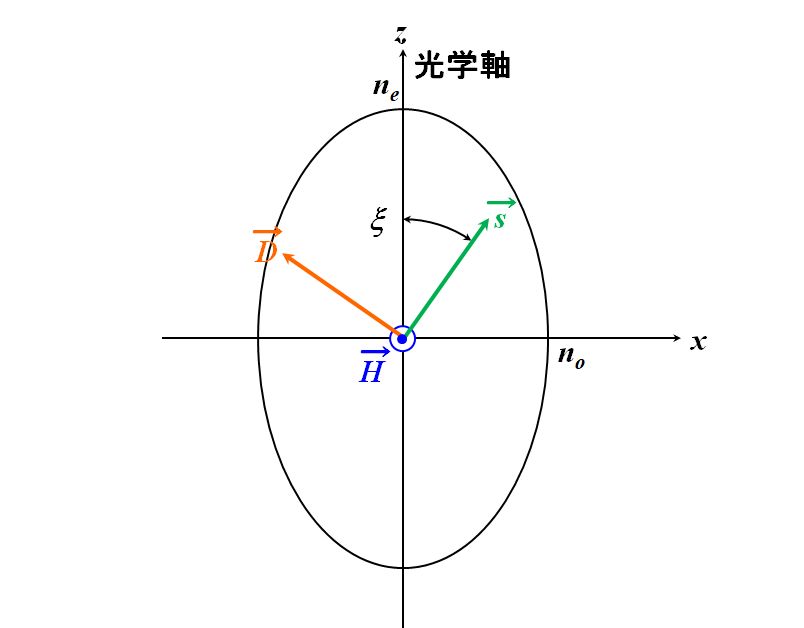 図2.8.4 光学軸と波数ベクトルの関係 このとき、光学軸と波数ベクトルのなす角を\(\xi\)と置きましょう。 |
|
 | そうすると、\(\vec{\mathstrut s}=(s_x,s_y,s_z)=(\sin\xi,0,\cos\xi)\)ですね。 | |
 | 電束密度と波数ベクトルは直交していたので、 \[ \vec{\mathstrut D} \cdot \vec{\mathstrut s} = D_x s_x + D_z s_z = 0 \quad \Leftrightarrow \quad - \frac{D_z}{D_x} = \frac{ s_x }{ s_z } = \frac{ \sin \xi }{ \cos \xi } = \tan \xi \tag{2.8.3} \] が成立します。 | |
 | そうですね。 | |
 | 一方、磁場成分は\(y\)軸に平行ですので、\(\vec{\mathstrut H}=(0,H_y,0)\)としてもいいですね?? | |
 | はい。 | |
 |
常光線については電場と電束密度が同じ向きですから、そのPoyntingベクトル\(\vec{\mathstrut S_o}\)が電場(電束密度)と磁場の両方に直交していることを考慮すれば、常光線の進む向きは図2.8.4の波数ベクトルの向きと一致します。
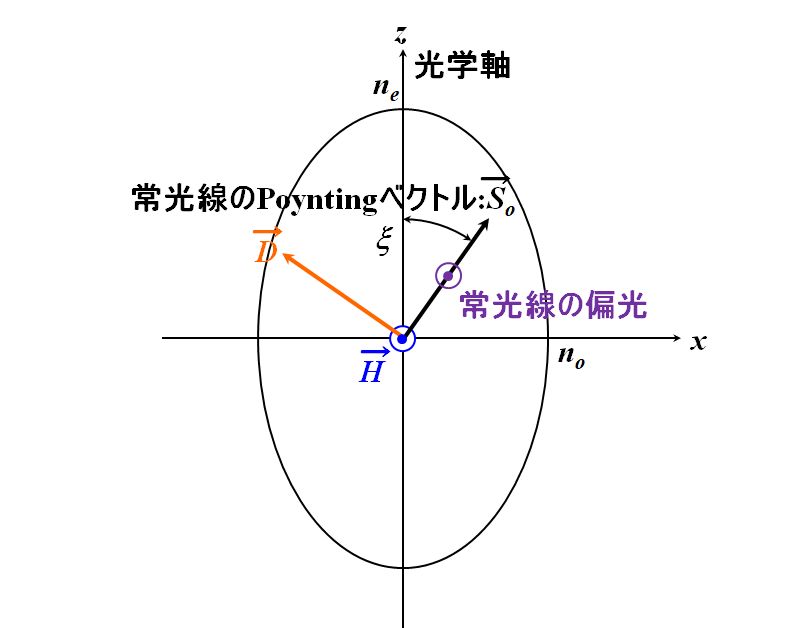 図2.8.5 常光線のPoyntingベクトル つまり、\(y\)軸に平行な偏光成分は波数ベクトルに沿ってエネルギーを伝搬させるということです。 |
|
 | そうすると、異常光線については、電場が\(\vec{\mathstrut E}=(\cfrac{D_x}{\varepsilon_o},0,\cfrac{D_z}{\varepsilon_e})\)だから、異常光線のPoyntingベクトル\(\vec{\mathstrut S_e}\)は、 \[ \vec{\mathstrut S_e} = \vec{\mathstrut E} \times \vec{\mathstrut H} = \left( \frac{D_x}{\varepsilon_o}, 0, \frac{D_z}{\varepsilon_e} \right) \times \left( 0, H_y, 0 \right) = \left( - \frac{D_z H_y}{\varepsilon_e}, 0, \frac{D_x H_y}{\varepsilon_o} \right) \] かな。 | |
 |
常光線と異常光線の分離角を\(\gamma\)とすると、
\[
\tan \left( \xi - \gamma \right) = \frac{{S_e}^{\left(x\right)}}{{S_e}^{\left(z\right)}} = - \frac{D_z H_y}{\varepsilon_e} \div \frac{D_x H_y}{\varepsilon_o} = - \frac{\varepsilon_o}{\varepsilon_e} \frac{D_z}{D_x} \tag{2.8.4}
\]
となります。
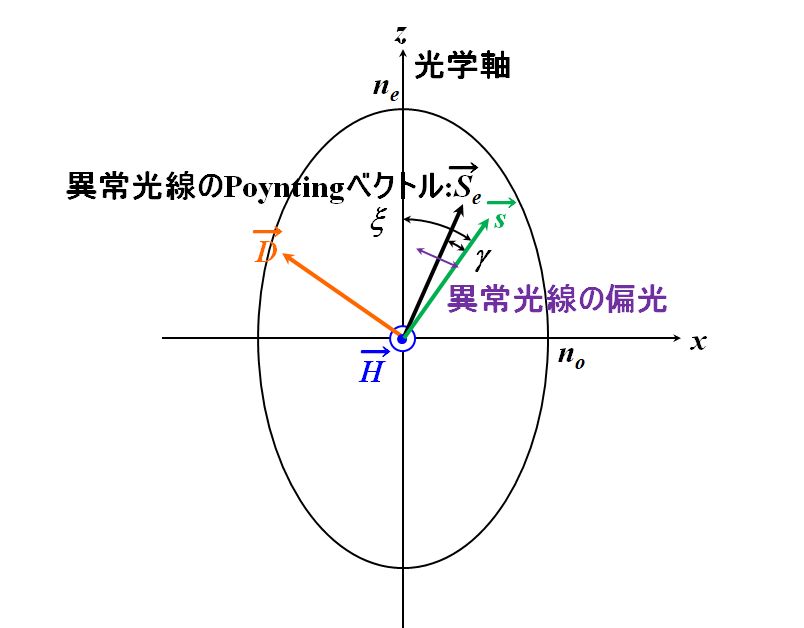 図2.8.6 異常光線のPoyntingベクトル つまり、\(xz\)平面に平行な偏光成分は、波数ベクトルに対して\(\gamma\)だけ分離してエネルギーを伝搬させるということです。 |
|
 | まとめると、一軸結晶に入射した光は、偏光が直交している常光線と異常光線に分かれて、それぞれが常光線屈折率\(n_o\)と、入射角に依存する屈折率\(n^{\thinspace \prime}\)(\(n_o\sim n_e\))を感じながら結晶内を伝搬するわけですね。 | |
 |
ですから、図2.8.7のような光学軸を持つ一軸結晶に光が垂直入射したとき、常光線と異常光線がどう振る舞うかというと―。
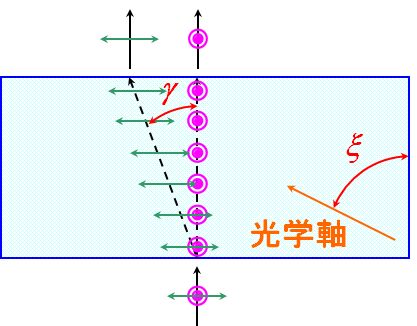 図2.8.7 常光線と異常光線の伝搬 |
|
 | ムムム。異常光線は、垂直入射なのに曲がって伝搬する??てことは、Snellの法則を満たしてない?!?! | |
 |
それこそ、異常光線の異常たる所以ですね。こういう一軸結晶の典型が方解石と呼ばれる鉱物です。
 図2.8.8 方解石 |
|
 | あ、文字が2重になって見えてる。 | |
 |
ですから、例えば文字の代わりに赤ドットを観察したとすると、方解石から出てくる像は偏光方向が直交している2つの赤ドットとして見えるはずです。そして、方解石の後ろに直線偏光子を置いてクルクルまわしてやると、片方の直線偏光と透過軸が一致したときには、もう片方の赤ドットが消失することになるのです。
|
|
 | へぇ、面白〜い。 | |
 | さて、式2.8.3と式2.8.4から分離角\(\gamma\)を出してみましょう。 | |
 | ん〜。式2.8.4に式2.8.3を代入できそうですね。 \[ \tan \left( \xi - \gamma \right) = - \frac{\varepsilon_o}{\varepsilon_e} \frac{D_z}{D_x} = \frac{\varepsilon_o}{\varepsilon_e} \tan \xi \] \[ \Leftrightarrow \quad \gamma = \xi - \tan^{-1} \left( \frac{\varepsilon_o}{\varepsilon_e} \tan \xi\right) \approx \xi - \tan^{-1} \left[ \left( \frac{n_o}{n_e} \right)^2 \tan \xi\right] \tag{2.8.5} \] | |
 | 式2.8.5を眺めると、常光線と異常光線が分離しない(\(\gamma=0\))条件が3つあることが分かります。 | |
 | 3つ??3つも?? | |
 | 3つです。 | |
 | 1つ目は、\(n_o=n_e\)のケースですよねぇ。このときは、\(\tan^{-1}\left(\tan\xi\right)=\xi\)になるから、\(\gamma=0\)ですもんね。 | |
 | 1つ目は正解です。それは要するに、等方性媒質ってことですから、当然の結果です。 | |
 | 2つ目は、\(\xi=0^{\circ}\)のときかなぁ。\(\tan\xi=0\)になるから、\(\gamma=0\)ですよね。 | |
 | 2つ目も正解です。それは、波数ベクトルが光学軸と一致していることを意味するので、光は等方性媒質だと騙されていることになり、分離しません。 |
〜波長板の正体とは??〜
 | え〜、もう1つ??本当にあります?? | |
 | \(\xi=90^{\circ}\)のときですね。このときは、\(\tan^{-1}\left[\left(\cfrac{n_o}{n_e}\right)^2\tan\xi\right]=90^{\circ}\)になるから、\(\gamma=0\)になりますよ。 | |
 | お〜、確かに。 | |
 |
このケースは非常に特殊で、常光線と異常光線は分離しないけど、それぞれは異なる屈折率\(n_o\)と\(n_e\)を感じながら伝搬している状況になっています。
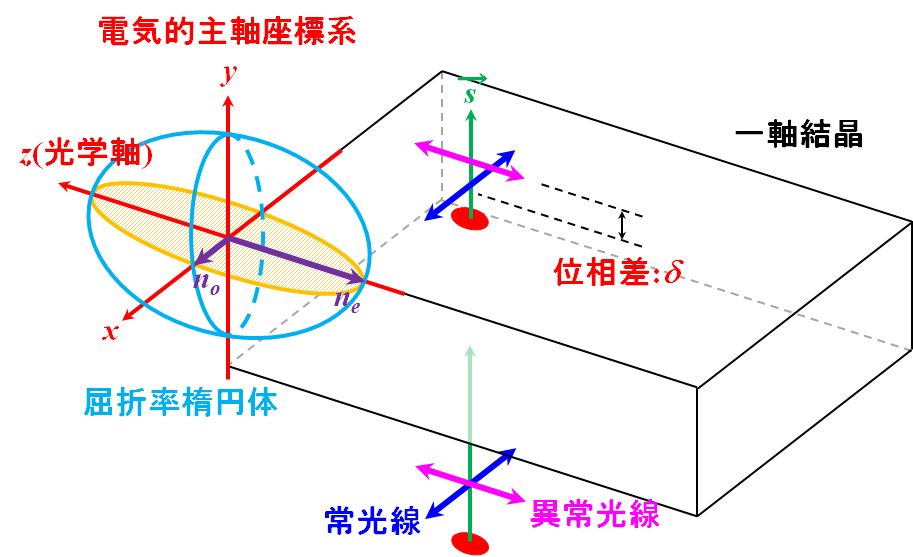 図2.8.9 \(\xi=90^{\circ}\)のときの状況 屈折率楕円体と組み合わせると、図2.8.9のようになっているわけですね。 |
|
 | \(n_o\neq n_e\)だから、一軸結晶の内部を通過するときの常光線、異常光線の位相速度が違いますよね。ん??ひょっとして、一軸結晶を抜ける前後で、直交する2つの偏光に位相差が付くのかな?? | |
 | 結晶の厚みを\(d\)とすれば、その位相差\(\delta\)は、 \[ \delta = \frac{2 \pi}{\lambda} \left( n_e - n_o \right) d \tag{2.8.6} \] と表されます。これをリタデーションと言います。 | |
 | ということは、一軸結晶を使うと偏光を変換させることができそうですよね。 | |
 |
なかなかのご明察ですね。例えば、リタデーション=\(\cfrac{\pi}{2}\)となるように\(d\)を設計すれば、それが1/4波長板の正体です。
 図2.8.10 波長板 |
|
 | てことは、リタデーション=\(\pi\)となるように\(d\)を設計すれば、1/2波長板の一丁あがりですね。 | |
 | リタデーションから、波長板はどんな波長でも同じ機能が発揮されるわけではない、ということも分かりますね?? | |
 | そうか、波長依存性がありますもんね。 | |
 | また、光学軸の向きが重要です。だから、波長板の取り付け方を間違えると、やはり所望の機能は発揮されません。 | |
 | それは、分かるようになっているんですか?? | |
 | たいていは図面で指示しますね。例えば、4隅の1つだけを斜めにカットするとか、コバの部分にマーキングするとか、そうやって組み付けるときに間違いのないように工夫するのです。ただのガラス板のように適当に扱うとダメなんですよ。 | |
 | そっか。気を付けよう…。 |
| 前頁へ | 戻る | 次頁へ |