 | 今回は、異方性媒質を簡単に理解する必殺技が明かされるんですね?? | |
 | 必殺技…。まぁ、そうかもしれませんね。まず、電場のエネルギー密度\(w_e\)が、 \[ w_e = \frac{1}{2} \vec{\mathstrut D} \cdot \vec{\mathstrut E} \tag{2.7.11} \] で与えられることに注目します。これに式1.8.5を加味すると、異方性媒質の場合はどのようになりますか?? | |
 | 式2.7.3を代入するだけでは?? \[ \begin{align*} w_e &= \frac{1}{2} \left( D_x E_x + D_y E_y + D_z E_z \right) = \frac{1}{2} \left( \frac{{D_x}^2}{\varepsilon_x} + \frac{{D_y}^2}{\varepsilon_y} +\frac{{D_z}^2}{\varepsilon_z} \right) \\ &\approx \frac{1}{2 \varepsilon_0} \left( \frac{{D_x}^2}{{n_x}^2} + \frac{{D_y}^2}{{n_y}^2} +\frac{{D_z}^2}{{n_z}^2} \right) \tag{2.7.12} \end{align*} \] | |
 | ここで、 \[ x \equiv \frac{D_x}{\sqrt{2 w_e {\varepsilon}_0}} \quad y \equiv \frac{D_y}{\sqrt{2 w_e {\varepsilon}_0}} \quad z \equiv \frac{D_z}{\sqrt{2 w_e {\varepsilon}_0}} \] とすると、式2.7.12は、 \[ \frac{x^2}{{n_x}^2} + \frac{y^2}{{n_y}^2} +\frac{z^2}{{n_z}^2} = 1 \tag{2.7.13} \] となります。 | |
 | 見掛けはすっきりしましたね。 | |
 |
式2.7.13を図示すると、図2.7.2のような楕円体になります。
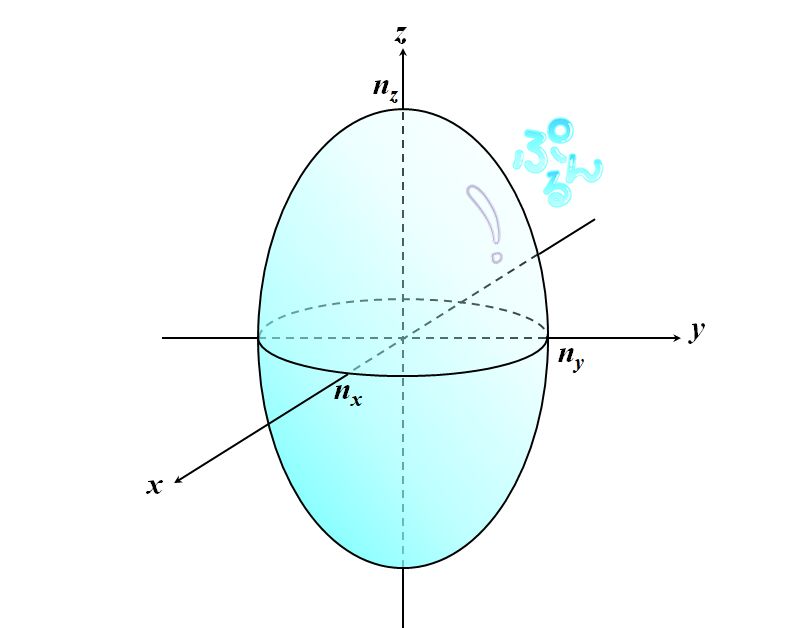 図2.7.2 屈折率楕円体 よって、この楕円体のことを屈折率楕円体と言います。 |
|
 | 偏光のときにPoincarè球ってやったけど、ここでも図形的解釈ができるってことかぁ。 | |
 |
図形的解釈の方が直感的で便利です。ルールは次のとおりです。 ①波数ベクトルの始点を、原点に一致させよ 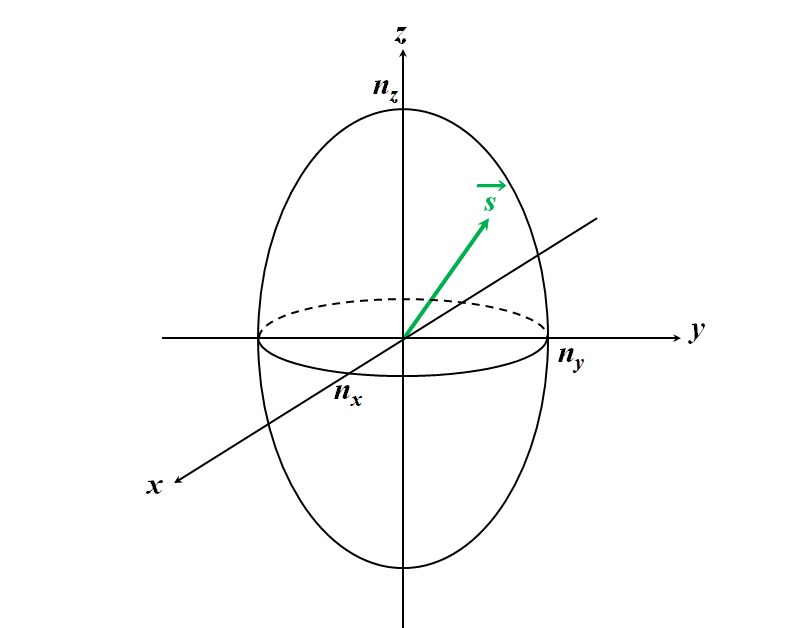 図2.7.3 波数ベクトルの始点を原点に一致させる ②波数ベクトルを法線とする平面Pで屈折率楕円体を切断せよ 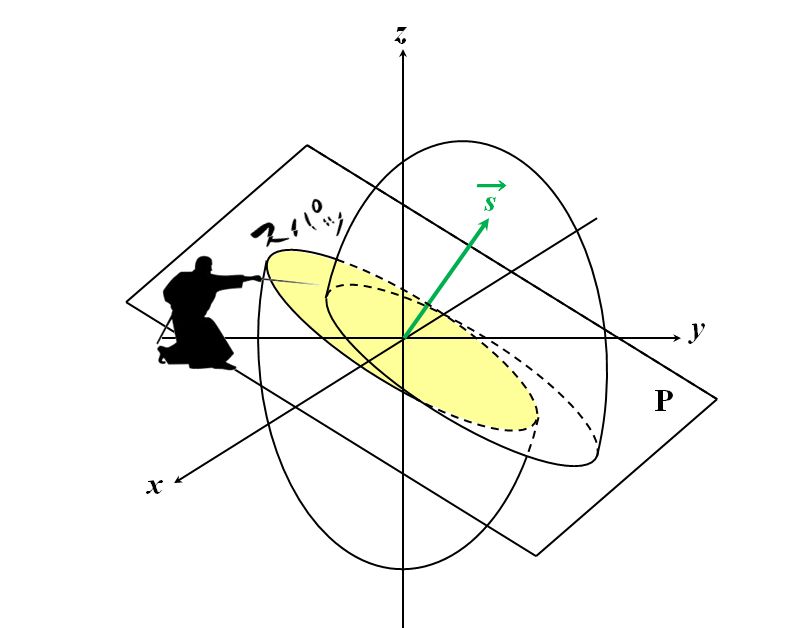 図2.7.4 波数ベクトルを法線とする平面Pで屈折率楕円体を切断する ③断面は楕円なので、その長軸と短軸の長さを読み取れ 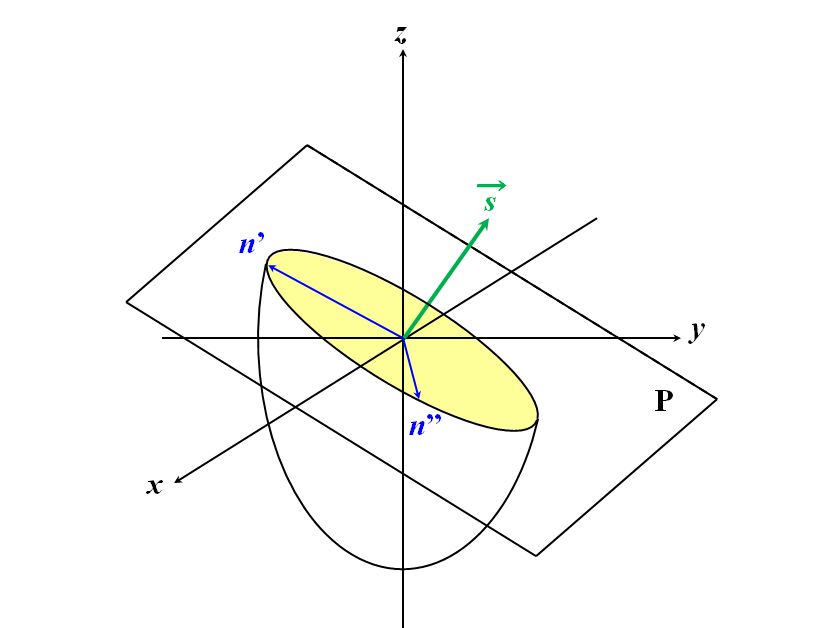 図2.7.5 楕円の長軸と短軸の長さを読み取る ④その2つの長さが求める屈折率\(n^{\thinspace \prime}\)と\(n^{\thinspace \prime\prime}\)である |
|
 | 手続きは簡単そうですね。でも、屈折率楕円体を原点を通る平面で切断したら、切り口は楕円になるんですか?? | |
 | その証明は簡単ですね。切断面の方程式は、 \[ s_x x + s_y y + s_z z = 0 \tag{2.7.14} \] ですから、これを次のように変形して、式2.7.13に代入します。 \[ z = - \frac{ s_x x + s_y y }{ s_z } \] | |
 | 代入か…。 \[ \frac{x^2}{{n_x}^2} + \frac{y^2}{{n_y}^2} + \frac{\left( s_x x + s_y y \right)^2}{{s_z}^2 {n_z}^2} = \frac{x^2}{{n_x}^2} + \frac{y^2}{{n_y}^2} + \frac{ {s_x}^2 x^2 + 2 s_x s_y xy + {s_y}^2 y^2 }{{s_z}^2 {n_z}^2} \\ = \left( \frac{1}{{n_x}^2} + \frac{ {s_x}^2 }{{s_z}^2 {n_z}^2} \right) x^2 + \frac{ 2 s_x s_y }{{s_z}^2 {n_z}^2} xy + \left( \frac{1}{{n_y}^2} + \frac{ {s_y}^2 }{{s_z}^2 {n_z}^2} \right) y^2 = 1 \] になりましたけど。 | |
 | この式が楕円であることは分かりますか?? | |
 | 前にやった2次曲線の判別式を計算してみればいいのでは?? \[ \left( \frac{1}{{n_x}^2} + \frac{ {s_x}^2 }{{s_z}^2 {n_z}^2} \right) \left( \frac{1}{{n_y}^2} + \frac{ {s_y}^2 }{{s_z}^2 {n_z}^2} \right) - \left( \frac{ s_x s_y }{{s_z}^2 {n_z}^2} \right)^2 \\ = \frac{1}{{n_x}^2{n_y}^2} + \frac{1}{ {s_z}^2 {n_z}^2} \left( \frac{ {s_x}^2 }{ {n_y}^2 } + \frac{ {s_y}^2 }{ {n_x}^2 } \right) + \frac{ {s_x}^2 {s_y}^2 }{ {s_z}^4 {n_z}^4 } - \frac{ {s_x}^2 {s_y}^2 }{{s_z}^4 {n_z}^4} \\ = \frac{1}{{n_x}^2{n_y}^2} + \frac{1}{ {s_z}^2 {n_z}^2} \left( \frac{ {s_x}^2 }{ {n_y}^2 } + \frac{ {s_y}^2 }{ {n_x}^2 } \right) \geq 0 \] だから、楕円ですね。 | |
 | \(xy\)平面に投影した形状が楕円ですから、断面も楕円であると言えます。 | |
 | じゃぁ、長軸と短軸の長さが、求めている屈折率になるというのは?? | |
 |
それを証明するには、その屈折率がFresnel方程式を満たすかどうかをチェックすればいいのです。いろいろやり方はありますが、ここではLagrangeの未定乗数法という数学テクニックを使うことにしましょう。
 Joseph-Louis Lagrange(1736~1813) |
|
 | 未定乗数法?? | |
 | 等式制約つきの関数の最大、最小問題を解くための方法ですね。 | |
 | ふ~ん。 | |
 | ここでは、式2.7.13と式2.7.14が等式制約になります。そして、\(x^2+y^2+z^2=r^2\)という球体を考え、この最大値と最小値を求める、というふうに問題を読み替えてやるわけです。 | |
 | その最大値と最小値が、切断面(楕円)の長軸と短軸に対応するわけですね。 | |
 | そこで、係数\(\Gamma_1\)と\(\Gamma_2\)を用いて、 \[ F = x^2 + y^2 + z^2 + \Gamma_1 \left( s_x x + s_y y+ s_z z \right) + \Gamma_2 \left( \frac{x^2}{{n_x}^2} + \frac{y^2}{{n_y}^2} + \frac{z^2}{{n_z}^2} - 1\right) \] という関数\(F\)を考えます。この関数\(F\)の極値は、それぞれの変数の偏微分が\(0\)になるときですよね?? | |
 | ということは、 \[ \left\{ \ \begin{array}{l} \cfrac{\partial F}{\partial x} = 2 x + \Gamma_1 s_x + 2 \Gamma_2 \cfrac{x}{{n_x}^2} = 0 \\ \cfrac{\partial F}{\partial y} = 2 y + \Gamma_1 s_y + 2 \Gamma_2 \cfrac{y}{{n_y}^2} = 0 \\ \cfrac{\partial F}{\partial z} = 2 z + \Gamma_1 s_z + 2 \Gamma_2 \cfrac{z}{{n_z}^2} = 0 \end{array} \right. \tag{2.7.15} \] ですね。 | |
 | 第1式に\(x\)、第2式に\(y\)、第3式に\(z\)を掛けて、すべて足してください。 | |
 | こうかな。 \[ 2 \left( x^2 + y^2 + z^2 \right) + \Gamma_1 \left( s_x x + s_y y + s_z z \right) + 2 \Gamma_2 \left( \frac{x^2}{{n_x}^2} + \frac{y^2}{{n_y}^2} + \frac{z^2}{{n_z}^2} \right) \\ = 2 r^2 + 2 \Gamma_2 = 0 \] | |
 | 今度は、第1式に\(s_x\)、第2式に\(s_y\)、第3式に\(s_z\)を掛けて、すべて足してください。 | |
 | こうですね。 \[ 2 \left( s_x x + s_y y + s_z z \right) + \Gamma_1 \left( {s_x}^2 + {s_y}^2 + {s_z}^2 \right) + 2 \Gamma_2 \left( \frac{s_x x}{{n_x}^2} + \frac{s_y y}{{n_y}^2} + \frac{s_z z}{{n_z}^2} \right) \\ = \Gamma_1 + 2 \Gamma_2 \left( \frac{s_x x}{{n_x}^2} + \frac{s_y y}{{n_y}^2} + \frac{s_z z}{{n_z}^2} \right) = 0 \] | |
 | そうすると、\(\Gamma_1\)と\(\Gamma_2\)が求まりますね?? | |
 | そっか。 \[ \left\{ \ \begin{array}{l} \Gamma_1 = 2 r^2 \left( \cfrac{s_x x}{{n_x}^2} + \cfrac{s_y y}{{n_y}^2} + \cfrac{s_z z}{{n_z}^2} \right) \\ \Gamma_2 = - r^2 \end{array} \right. \] | |
 | これを式2.7.15に代入するのです。 | |
 | ん~と。 \[ \left\{ \ \begin{array}{l} 2 x + 2 r^2 \left( \cfrac{s_x x}{{n_x}^2} + \cfrac{s_y y}{{n_y}^2} + \cfrac{s_z z}{{n_z}^2} \right) s_x - 2 r^2 \cfrac{x}{{n_x}^2} = 0 \\ 2 y + 2 r^2 \left( \cfrac{s_x x}{{n_x}^2} + \cfrac{s_y y}{{n_y}^2} + \cfrac{s_z z}{{n_z}^2} \right) s_y - 2 r^2 \cfrac{y}{{n_y}^2} = 0 \\ 2 z + 2 r^2 \left( \cfrac{s_x x}{{n_x}^2} + \cfrac{s_y y}{{n_y}^2} + \cfrac{s_z z}{{n_z}^2} \right) s_z - 2 r^2 \cfrac{z}{{n_z}^2} = 0 \end{array} \right. \] かな。 | |
 | 行列で書き直せませんか?? | |
 | ん~。書き直せるか…。 \[ \left( \begin{array}{ccc} 1 - \cfrac{r^2}{{n_x}^2} + \cfrac{{s_x}^2 r^2}{{n_x}^2} & \cfrac{{s_x}{s_y} r^2}{{n_y}^2} & \cfrac{{s_x}{s_z} r^2}{{n_z}^2} \\ \cfrac{{s_y}{s_x} r^2}{{n_x}^2} & 1 - \cfrac{r^2}{{n_y}^2} + \cfrac{{s_y}^2 r^2}{{n_y}^2} & \cfrac{{s_y}{s_z} r^2}{{n_z}^2} \\ \cfrac{{s_z}{s_x} r^2}{{n_x}^2} & \cfrac{{s_z}{s_y} r^2}{{n_y}^2} & 1 - \cfrac{r^2}{{n_z}^2} + \cfrac{{s_z}^2 r^2}{{n_z}^2} \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = 0 \] | |
 | \((x,y,z)\neq0\)ですから、この方程式を満たすには行列式が\(0\)でないといけません。 | |
 | 前回もやったな。途中計算は省いて結果だけ書くと、 \[ \left( {n_y}^2 - r^2 \right) \left( {n_z}^2 - r^2 \right) {s_x}^2{n_x}^2 \\ \quad +\left( {n_z}^2 - r^2 \right) \left( {n_x}^2 - r^2 \right) {s_y}^2{n_y}^2 \\ \quad \quad +\left( {n_x}^2 - r^2 \right) \left( {n_y}^2 - r^2 \right) {s_z}^2{n_z}^2 = 0 \tag{2.7.16} \] で、式2.7.10と同じですね。なるほど、Fresnel方程式が満たされることが証明できましたね。 | |
 | 式2.7.13から、媒質の屈折率のありようは3種類あることが分かります。1つ目は\(n_x=n_y=n_z\)です。 | |
 | それは等方性ですね。屈折率楕円体は球形になるわけか。 | |
 | 2つ目は、どれか1つだけ仲間外れ、というタイプです。これを1軸結晶と言います。 | |
 | じゃぁ、全部バラバラの屈折率だったら2軸結晶?? | |
 | 正解ですね。 | |
 | 教授。ここで言っている"軸"って何のことですか?? | |
 | いい質問ですね。その正体については次回、1軸結晶を取り上げたときに明かすことにしましょう。 |
| 前頁へ | 戻る | 次頁へ |