 | |
異方性??
|
 | |
これまでの媒質は、光の入射角に関係なく屈折率はただ1つしかありませんでした。
|
 | |
そりゃ、そうですよ。
|
 | |
光学的に異方性である、というのは入射角に対して屈折率が変化する性質のことを指します。
|
 | |
え??そんな厄介な媒質があるんですか??
|
 | |
あります。だから、入射角に依存して、光がどんな屈折率を感じているか読み解かないといけません。
|
 | |
う〜ん。何か面倒なことになりそうな予感しかないんですけど。
|
 | |
その予感は正しいですね。異方性は力学での応力に対応するもので、取り扱いにはテンソルの知識が必要です。
\[
\varepsilon=
\left(
\begin{array}{ccc}
\varepsilon_{11} & \varepsilon_{21} & \varepsilon_{31} \\
\varepsilon_{21} & \varepsilon_{22} & \varepsilon_{32} \\
\varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33}
\end{array}
\right) \tag{2.7.1}
\]
これを誘電率テンソルと言います。
|
 | |
テンソル??聞いたことないですよ。
|
 | |
ま、普通はそうでしょう。最近では行列すら高校数学のカリキュラムから外されてますからね。ただ、光学で扱う誘電率テンソルは1つ嬉しい事実があります。
|
 | |
ん??本当??
|
 | |
まず、エネルギー保存則から誘電率テンソルは対称テンソルであることが導けます。そして、対称テンソルは座標軸を適切に設定すると、
\[
\varepsilon=
\left(
\begin{array}{ccc}
\varepsilon_x & 0 & 0 \\
0 & \varepsilon_y & 0 \\
0 & 0 & \varepsilon_z
\end{array}
\right) \tag{2.7.2}
\]
という形に変形することができるのです。
|
 | |
お〜、殆ど\(0\)になった〜。
|
 | |
つまり、異方性媒質には、誘電体テンソルが対角行列の形に整理できる座標軸の取り方が存在する、ということなんですよ。この座標軸のことを電気的主軸座標系と言い、対角成分の誘電率のことを主誘電率と言います。
|
 | |
入射する光の座標系の取り方は任意だから、異方性媒質を扱うときは電気的主軸座標系を採用すれば、議論が簡単になるってことですね。
|
 | |
式2.7.2を式1.3.8に代入すると、
\[
\left(
\begin{array}{c}
D_x \\
D_y \\
D_z
\end{array}
\right)=
\left(
\begin{array}{ccc}
\varepsilon_x & 0 & 0 \\
0 & \varepsilon_y & 0 \\
0 & 0 & \varepsilon_z
\end{array}
\right)
\left(
\begin{array}{c}
E_x \\
E_y \\
E_z
\end{array}
\right)=
\left(
\begin{array}{c}
\varepsilon_x E_x \\
\varepsilon_y E_y \\
\varepsilon_z E_z
\end{array}
\right) \tag{2.7.3}
\]
となります。
|
 | |
あれれ。そうすると、電場\(\vec{\mathstrut E}\)と電束密度\(\vec{\mathstrut D}\)は同じ向きじゃないってこと??
|
 | |
そうです。異方性媒質中では、電場\(\vec{\mathstrut E}\)と電束密度\(\vec{\mathstrut D}\)は同じ向きになりません。このことから、波数ベクトル\(\vec{\mathstrut k}\)(或いは、その単位ベクトル\(\vec{\mathstrut s}\))やPoyntingベクトル\(\vec{\mathstrut P}\)も、今まで勝手にいろいろなことを前提として議論していたのではないか、という疑いが出てきます。
|
 | |
それは、例えば波数ベクトルとPoyntingベクトルが同じ向きでないかもしれないとか、そういうこと??
|
 | |
はい。というわけで、電場、磁場、波数ベクトル、Poyntingベクトル、電束密度などの関係性を、異方性媒質を含むように抜本的に見直すことにしましょう。
|
 | |
大規模修繕工事だ…。
|
 | |
まず、式1.11.4を導出したときのことを思い出してほしいんですが、これと同じようなことを式1.4.1からアプローチします。
\[
\nabla \times \vec{\mathstrut H} = \varepsilon \frac{ \partial \vec{\mathstrut E} }{ \partial t } \tag{1.4.1}
\]
|
 | |
ん〜。そうすると、左辺は電場とのアナロジーで、
\[
\nabla \times \vec{\mathstrut H} = i \vec{\mathstrut k} \times \vec{\mathstrut H} \tag{2.7.4}
\]
でいいですか??
|
 | |
OKですね。では、右辺は??
|
 | |
やっぱり、電場とのアナロジーで、
\[
\varepsilon \frac{ \partial \vec{\mathstrut E} }{ \partial t } = - i \omega \varepsilon \vec{\mathstrut E} \tag{2.7.5}
\]
かな。
|
 | |
とすると、式1.4.1は??
|
 | |
こんな感じ。
\[
\vec{\mathstrut k} \times \vec{\mathstrut H} = - \omega \varepsilon \vec{\mathstrut E} \tag{2.7.6}
\]
|
 | |
では、式1.11.4に\(\vec{\mathstrut k}\times\)を演算しましょう。
|
 | |
そうすると…。
\[
\vec{\mathstrut k} \times \vec{\mathstrut k} \times \vec{\mathstrut E} = \omega \mu \vec{\mathstrut k} \times \vec{\mathstrut H} \tag{2.7.7}
\]
ですね。
|
 | |
式2.7.7の左辺はベクトル三重積の公式を使うと、
\[
\begin{align*}
\vec{\mathstrut k} \times \vec{\mathstrut k} \times \vec{\mathstrut E} &= \big( \vec{\mathstrut k} \cdot \vec{\mathstrut E} \big) \vec{\mathstrut k} - \big( \vec{\mathstrut k} \cdot \vec{\mathstrut k} \big) \vec{\mathstrut E} = k^2 \big( \vec{\mathstrut s} \cdot \vec{\mathstrut E} \big) \vec{\mathstrut s} - k^2 \vec{\mathstrut E} \\
&= k^2 \Big[ \big( \vec{\mathstrut s} \cdot \vec{\mathstrut E} \big) \vec{\mathstrut s} - \vec{\mathstrut E} \Big]
\end{align*}
\]
です。一方、式2.7.7の右辺に式2.7.6を代入すると??
|
 | |
え〜っと。
\[
\omega \mu \vec{\mathstrut k} \times \vec{\mathstrut H} = - \omega^2 \mu \varepsilon \vec{\mathstrut E} = - \omega^2 \mu \vec{\mathstrut D}
\]
|
 | |
つまり、式2.7.7は??
|
 | |
式1.11.6があるから、
\[
k^2 \Big[ \big( \vec{\mathstrut s} \cdot \vec{\mathstrut E} \big) \vec{\mathstrut s} - \vec{\mathstrut E} \Big] = - \omega^2 \mu \vec{\mathstrut D}
\quad \Leftrightarrow \quad \big( \vec{\mathstrut s} \cdot \vec{\mathstrut E} \big) \vec{\mathstrut s} - \vec{\mathstrut E} = - {v_p}^2 \mu \vec{\mathstrut D} \tag{2.7.8}
\]
|
 | |
更に、式1.4.7、式1.8.5を使うと、式2.7.8の右辺は、
\[
{v_p}^2 \mu \vec{\mathstrut D} = \frac{1}{\varepsilon \mu} \mu \vec{\mathstrut D} = \frac{1}{\varepsilon} \vec{\mathstrut D} = \frac{1}{\varepsilon_0} \frac{\varepsilon_0}{\varepsilon} \vec{\mathstrut D} = \frac{1}{\varepsilon_0 \varepsilon_r} \vec{\mathstrut D} \approx \frac{1}{\varepsilon_0 n^2} \vec{\mathstrut D}
\]
ですからね。
|
 | |
そっか。まとめると、式2.7.8は、
\[
\big( \vec{\mathstrut s} \cdot \vec{\mathstrut E} \big) \vec{\mathstrut s} - \vec{\mathstrut E} = - \frac{1}{\varepsilon_0 n^2} \vec{\mathstrut D} \quad \Leftrightarrow \quad
\vec{\mathstrut D} = \varepsilon_0 n^2 \Big[ \vec{\mathstrut E} - \big( \vec{\mathstrut s} \cdot \vec{\mathstrut E} \big) \vec{\mathstrut s} \Big] \tag{2.7.9}
\]
ってことかな。
|
 | |
これが、電場\(\vec{\mathstrut E}\)、電束密度\(\vec{\mathstrut D}\)、波数の単位ベクトル\(\vec{\mathstrut s}\)の関係を示す一般式になります。式2.7.9から、少なくとも電場\(\vec{\mathstrut E}\)、電束密度\(\vec{\mathstrut D}\)、波数ベクトル\(\vec{\mathstrut k}\)は同一平面内にあることが分かります。また、式2.7.9の両辺に対して\(\vec{\mathstrut s}\)の内積をとると、
\[
\vec{\mathstrut D} \cdot \vec{\mathstrut s} = \varepsilon_0 n^2 \Big[ \vec{\mathstrut s} \cdot \vec{\mathstrut E} - \big( \vec{\mathstrut s} \cdot \vec{\mathstrut E} \big) \vec{\mathstrut s} \cdot \vec{\mathstrut s} \Big]
= \varepsilon_0 n^2 \Big[ \vec{\mathstrut s} \cdot \vec{\mathstrut E} - \vec{\mathstrut s} \cdot \vec{\mathstrut E} \Big] = 0
\]
になるので―。
|
 | |
電束密度\(\vec{\mathstrut D}\)と波数ベクトル\(\vec{\mathstrut k}\)が直交しているわけですね。
|
 | |
一方、Poyntingベクトルは、
\[
\vec{\mathstrut S} = \vec{\mathstrut E} \times \vec{\mathstrut H} \tag{2.3.2}
\]
でしたから、電場が電束密度に対して\(\gamma\)だけ傾ているとすれば、Poyintingベクトルも波数ベクトルに対して\(\gamma\)だけ傾ていることになります。
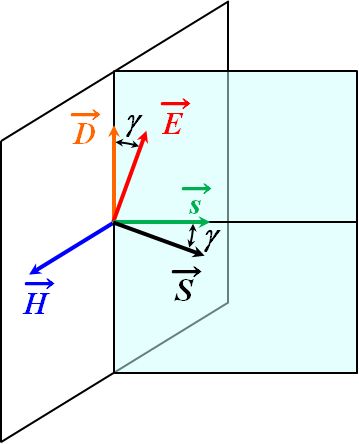
図2.7.1 結晶内における電場、磁場、電束密度、波数ベクトル、Poyntingベクトルの関係
|
 | |
光の進む向きとエネルギーの進む向きが違うのか。何だか複雑ですね…。
|
 | |
さて、式2.7.9を行列を使って書いてみましょう。右辺の括弧の中はどうなりますか??
|
 | |
括弧の中か…。
\[
\begin{align*}
\vec{\mathstrut E} - \big( \vec{\mathstrut s} \cdot \vec{\mathstrut E} \big) \vec{\mathstrut s} &=
\left(
\begin{array}{c}
E_x \\
E_y \\
E_z
\end{array}
\right) - \left( s_x E_x + s_y E_y + s_z E_z \right)
\left(
\begin{array}{c}
s_x \\
s_y \\
s_z
\end{array}
\right) \\
&=
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{c}
E_x \\
E_y \\
E_z
\end{array}
\right)
-
\left(
\begin{array}{ccc}
{s_x}^2 & s_x s_y & s_x s_z \\
s_y s_x & {s_y}^2 & s_y s_z \\
s_z s_x & s_z s_y & {s_z}^2
\end{array}
\right)
\left(
\begin{array}{c}
E_x \\
E_y \\
E_z
\end{array}
\right) \\
&=
\left(
\begin{array}{ccc}
1-{s_x}^2 & -s_x s_y & -s_x s_z \\
-s_y s_x & 1-{s_y}^2 & -s_y s_z \\
-s_z s_x & -s_z s_y & 1-{s_z}^2
\end{array}
\right)
\left(
\begin{array}{c}
E_x \\
E_y \\
E_z
\end{array}
\right)
\end{align*}
\]
|
 | |
一方、式2.7.9の左辺は式2.7.3ですから、
\[
\left(
\begin{array}{c}
\varepsilon_x E_x \\
\varepsilon_y E_y \\
\varepsilon_z E_z
\end{array}
\right)
= \varepsilon_0 n^2
\left(
\begin{array}{ccc}
1-{s_x}^2 & -s_x s_y & -s_x s_z \\
-s_y s_x & 1-{s_y}^2 & -s_y s_z \\
-s_z s_x & -s_z s_y & 1-{s_z}^2
\end{array}
\right)
\left(
\begin{array}{c}
E_x \\
E_y \\
E_z
\end{array}
\right)
\]
ということです。ここで、\({n_x}^2=\cfrac{\varepsilon_x}{\varepsilon_0}\)、\({n_y}^2=\cfrac{\varepsilon_y}{\varepsilon_0}\)、\({n_z}^2=\cfrac{\varepsilon_z}{\varepsilon_0}\)とすると―。
|
 | |
そうか。
\[
\varepsilon_0 \left(
\begin{array}{c}
{n_x}^2 E_x \\
{n_y}^2 E_y \\
{n_z}^2 E_z
\end{array}
\right)
= \varepsilon_0 n^2
\left(
\begin{array}{ccc}
1-{s_x}^2 & -s_x s_y & -s_x s_z \\
-s_y s_x & 1-{s_y}^2 & -s_y s_z \\
-s_z s_x & -s_z s_y & 1-{s_z}^2
\end{array}
\right)
\left(
\begin{array}{c}
E_x \\
E_y \\
E_z
\end{array}
\right)
\]
\[
\Leftrightarrow \quad \left(
\begin{array}{ccc}
{n_x}^2-n^2+{s_x}^2 n^2 & s_x s_y n^2 & s_x s_z n^2 \\
s_y s_x n^2 & {n_y}^2-n^2+{s_y}^2 n^2 & s_y s_z n^2 \\
s_z s_x n^2 & s_z s_y n^2 & {n_z}^2-n^2+{s_z}^2 n^2
\end{array}
\right)
\left(
\begin{array}{c}
E_x \\
E_y \\
E_z
\end{array}
\right) = 0
\]
ですね。
|
 | |
\(\vec{\mathstrut E}\neq0\)ですから、この方程式を満たすには行列式が\(0\)でないといけません。
|
 | |
行列式…。う〜ん、これは大変だ。途中計算は省いて結果だけ書くと、
\[
\left( {n_y}^2 - n^2 \right) \left( {n_z}^2 - n^2 \right) {s_x}^2{n_x}^2 \\
\quad +\left( {n_z}^2 - n^2 \right) \left( {n_x}^2 - n^2 \right) {s_y}^2{n_y}^2 \\
\quad \quad +\left( {n_x}^2 - n^2 \right) \left( {n_y}^2 - n^2 \right) {s_z}^2{n_z}^2 = 0 \tag{2.7.10}
\]
ですね。
|
 | |
この式をFresnel方程式と言います。式2.7.10は、\(n^2\)の2次方程式になっているので、\(n^2\)の解は2つ存在し、また\(n>0\)ですから、屈折率は2つ定義できます。つまり、異方性媒質の場合、光の感じる屈折率は2つあることになり、これを複屈折と言うのです。
|
 | |
ん〜。全然、簡単じゃなかったなぁ…。
|
 | |
理論的にしっかり議論しようとすれば、確かにそういう一面はあるとは思いますが、異方性媒質を直感的に理解するには、上手い方法があります。
|
 | |
お、それはいい知らせだ〜。
|
 | |
では、次回はその方法について議論しましょう。
|


















































