 | 教授。誘電体と金属でのエネルギー透過率、エネルギー反射率を議論してきましたけど、こんな七面倒なことを実際に使うことってあるんですか?? | |
 |
ありますよ。例えば、複写機やレーザ・プリンターに収納されているLSU(Laser scanning unit)の光学設計では非常に重要な意味を持ってきます。
 図2.6.1 LSUの例 |
|
 | 使うんだ…。 | |
 |
図2.6.1のLSUを主要な光学素子だけで展開すると図2.6.2のようになります。
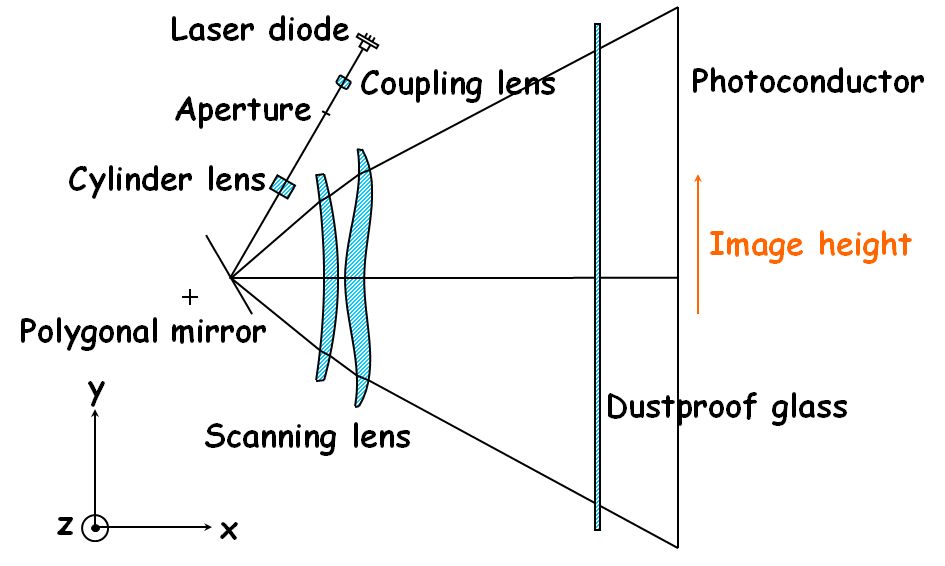 図2.6.2 走査光学系 |
|
 | 折返しミラーは省略されてますね。 | |
 | 折返しミラーは、光路を折り曲げて、狭い空間の中にLSUを収める機能しかありませんから、ここでは省いてます。さて、直感的には、半導体レーザ(LD)に与える電流量が一定であれば、発光する光量は一定だから、そのビームが感光体に到達した場合に、どの位置でも照射エネルギーは同じだと思えますよね?? | |
 | そうか。でも、実際は入射角依存性があるから、そうではないってことですね。 | |
 |
その説明を始める前に、LSUに使われるLDについて少し予備知識を仕込んでおきましょう。まずビームは、LDの活性層にある一点から放射されます。
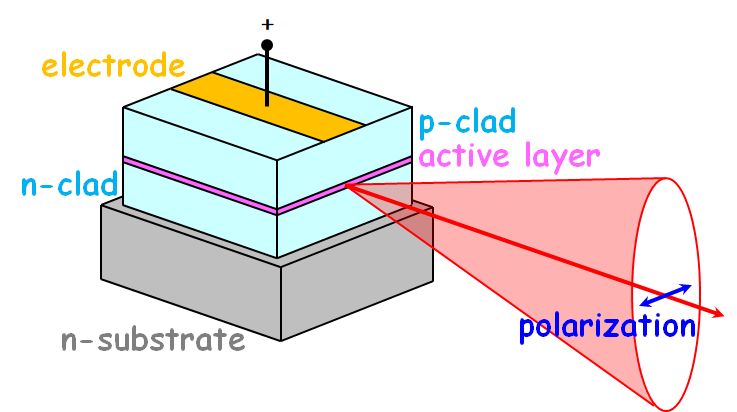 図2.6.3 LDの基本構造 このとき、ビームは活性層に平行な直線偏光になっている、ということを覚えておいてください。 |
|
 | ビームの広がりは、活性層に垂直な方向で広くなってますね。 | |
 | それは、回折による影響です。間口の狭い方が影響を強く受けるので、ビームの広がりパターンは楕円形状になるのです。 | |
 | 直線偏光の設置方向って、何か決まりがあるんですか?? | |
 | あります。しかし、その理由については別の機会にまわしましょう。ここでは、一般的にポリゴン・ミラーの回転軸と直線偏光の向きを一致させる、と覚えてもらえれば充分です。 | |
 |
入射ビームと反射ビームで張られる平面が入射平面だから、それに垂直ということは\(s\)偏光と見るわけですね??
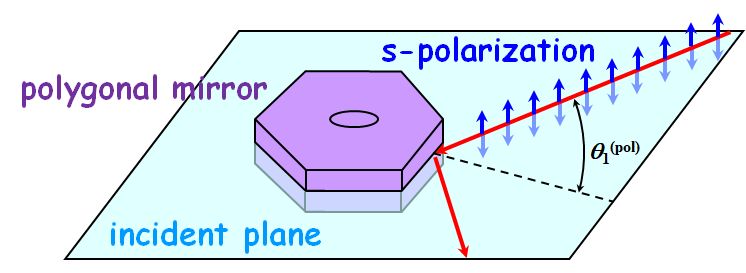 図2.6.4 ポリゴン・ミラーと入射光の関係 |
|
 | そうです。但し、\(s\)偏光となるようにLDを設置するのは一般論であって、設計の制約から\(p\)偏光になるようにLDを設置したり、その間の角度になるようにLDを設置することも稀にですがあり得ます。 | |
 | ふむふむ。 | |
 | 以上のことを頭に入れて、もう一度、図2.6.2を見てください。ポリゴン・ミラー以降の光学素子については、ポリゴン・ミラーの回転に伴って、ビームの入射角が変化します。 | |
 | 回転の方向は?? | |
 | ここでは、時計周りとしましょう。また、感光体の\(y\)座標に沿った位置を像高と呼びます。 | |
 | そうすると、ポリゴン・ミラーの回転に伴って、照射ビームはプラス像高からマイナス像高に走査されるわけですね?? | |
 |
はい。さて、ポリゴン・ミラーへ入射するビームの入射角\({\theta_1}^{\left({\rm pol}\right)}\)は、図2.6.5のように変化しています。
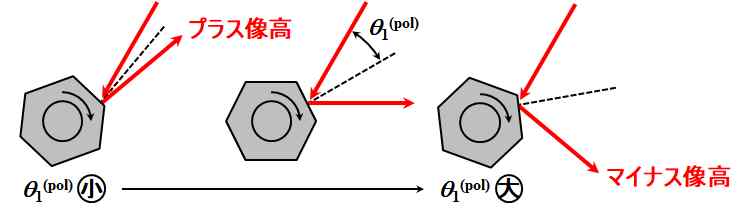 図2.6.5 ポリゴン・ミラーの入射角\({\theta_1}^{\left({\rm pol}\right)}\)変化 |
|
 | 入射角\({\theta_1}^{\left({\rm pol}\right)}\)って、どのくらい変化するんですか?? | |
 | 凡そ\(10^{\circ}\leq{\theta_1}^{\left({\rm pol}\right)}\leq50^{\circ}\)と考えておけばよいでしょう。 | |
 | ポリゴン・ミラーの材質は?? | |
 | アルミです。厳密には、それにSiO2などのコーティングがされていますが、ざっくり金属の反射と捉えておけば充分です。 | |
 |
そうすると、図2.5.6のうち、\(10^{\circ}\sim50^{\circ}\)を切り出した変化になるわけですね。
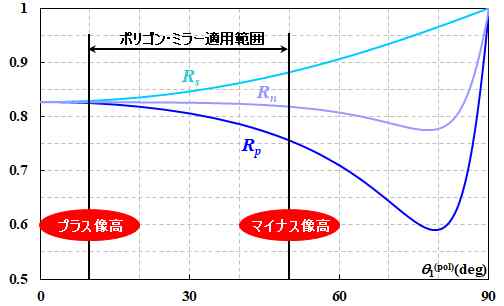 図2.6.6 ポリゴン・ミラーのエネルギー反射率(アルミ:\(1.44-i5.23\)) |
|
 | 次に、ポリゴン・ミラー以降の光学素子については、どうですか?? | |
 |
これは、中心に対して対称形状の素子ばっかりだから、例えば走査レンズL1の入射角\({\theta_1}^{\left({\rm L1}\right)}\)は、ポリゴン・ミラーの回転に伴って、垂直入射に向かって減少し、その後、また増加しそうですね。
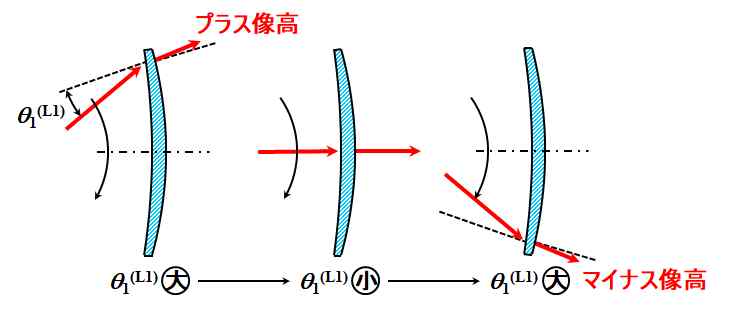 図2.6.7 走査レンズL1の入射角\({\theta_1}^{\left({\rm L1}\right)}\)変化 |
|
 |
そうなんですが、走査レンズL1の透過率という見方をした場合には、入射面だけでなく出射面も併せて考えないとダメですよ。ひとまず、入射面の効果だけを対象とするなら、入射角\({\theta_1}^{\left({\rm L1}\right)}\)は凡そ\(0^{\circ}\leq{\theta_1}^{\left({\rm L1}\right)}\leq25^{\circ}\)と考えればいいので、図2.3.5の\(0^{\circ}\sim25^{\circ}\)を切り出して、\(0^{\circ}\)のところで線対称となるようにコピーすればOKですね。
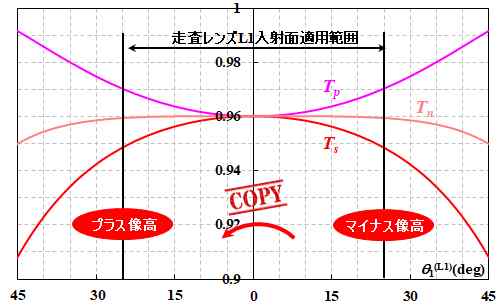 図2.6.8 走査レンズL1(入射面のみ)のエネルギー透過率 |
|
 | そっか。 | |
 |
図2.6.9は、\(s\)偏光のとき、各光学素子におけるエネルギー透過率、エネルギー反射率をコーティングも含めてシミュレーションしたものです。
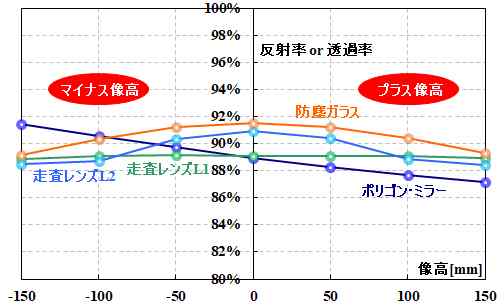 図2.6.9 \(s\)偏光のときのエネルギー透過率、エネルギー反射率 |
|
 | ビームの通過位置は、像高で正規化しているわけですね。だいたい、予想したとおりの変化になってそうかな。走査レンズL2はクネクネしてるけど。 | |
 | それは、レンズの形状が素直ではない(=自由曲面)ので、入射角もそれに応じて微妙に変化しているからですね。 | |
 | これ、\(p\)偏光だったらどうなるんですか?? | |
 |
同じようにシミュレーションしてみました。
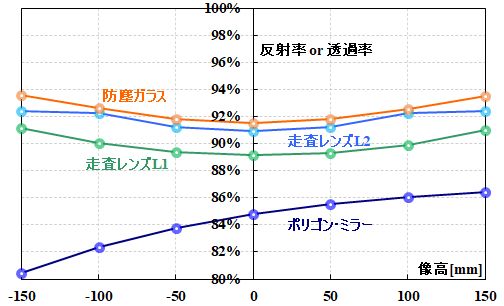 図2.6.10 \(p\)偏光のときのエネルギー透過率、エネルギー反射率 |
|
 | ポリゴン・ミラーの変化がかなり違いますね。 | |
 |
ついでに、円偏光の場合もシミュレーションしてあります。
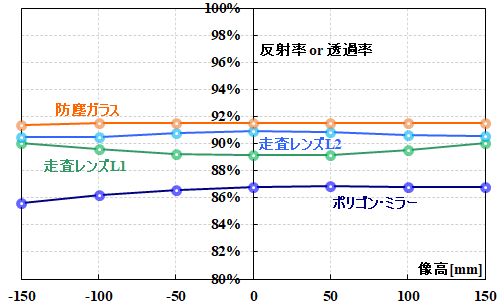 図2.6.11 円偏光のときのエネルギー透過率、エネルギー反射率 |
|
 | お〜、ポリゴン・ミラーのエネルギー反射率が改善してますね。 | |
 | 感光体の照射エネルギー\(P_{\rm img}(h)\)の変化は、例えば像高50mmであれば、各光学素子の像高50mmのエネルギー透過率、エネルギー反射率を読み取って、それらを掛け算すれば求まります。 | |
 | でも、絶対量より相対量の方が重要なんじゃないですか?? | |
 |
そこで、一般的には照射エネルギーの最大値で正規化します。
\[
S = \frac{ P_{\rm img}\left(h\right) - {P_{\rm img}}^{\left({\rm max}\right) }}{ {P_{\rm img}}^{\left({\rm max}\right) }} \tag{2.6.1}
\]
通常、明暗ムラのことを光学ではシェーディングと言うので、感光体の照射エネルギー相対値変化(\(S\))のことを、そのように呼びますね。
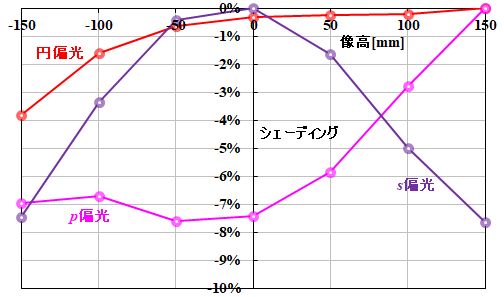 図2.6.12 シェーディング特性 |
|
 | 円偏光だと、結構フラットな変化になってますね。 | |
 | ですから、シェーディング特性をよくしたければ、直線偏光を円偏光に変換する光学素子を光路のどこかに挿入したくなるのですが、コストの観点からは避けたいですね。 | |
 | じゃぁ、別の代替案が必要ですね。 | |
 | 1つは、コーティング条件の最適化があるでしょう。尤も、これもコストの観点からは避けたいですが。 | |
 | シェーディング特性が図2.6.12のようになるのを見越して、LDに注入する電流量を変えたらどうですか?? | |
 | それがベストな解決手段かもしれないですね。 |
| 前頁へ | 戻る | 次頁へ |