 | 干渉の具体例を3つ紹介します。1つ目はYoungの干渉実験です。 | |
 |
これですね。
|
|
 |
たいていの教科書では、間隔\(h\)の2重スリットの垂直2等分線上に光源を置いて議論されますが、ここでは少し汎用性を持たせて、光源は\(\delta\)だけずれているとしましょう。
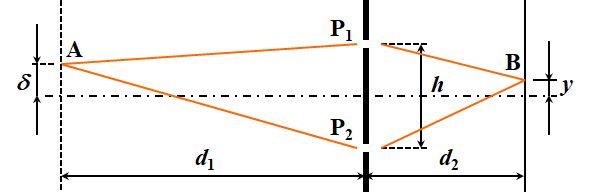 図3.1.3 Youngの干渉実験(1) |
|
 | スクリーン上の強度分布を求めるわけですね。 | |
 | 光は、スリットP2を通過するA→P2→Bと、スリットP1を通過するA→P1→Bの2つのパスが存在しますが、光源A〜スリットまでの\(d_1\)の範囲で光路長差\(\Delta l_1\)を求めてみましょう。 | |
 | そうすると…、 \[ \begin{align*} \Delta l_1 &= \sqrt{ {d_1}^2 + \left( \frac{h}{2} + \delta \right)^2 } - \sqrt{ {d_1}^2 + \left( \frac{h}{2} - \delta \right)^2 } \\ &\fallingdotseq \left[ d_1 + \frac{1}{2 d_1} \left( \frac{h}{2} + \delta \right)^2 \right] - \left[ d_1 + \frac{1}{2 d_1} \left( \frac{h}{2} - \delta \right)^2 \right] \\ &= \frac{h \delta}{d_1} \tag{3.1.8} \end{align*} \] ですね。 | |
 | 次は、スリット〜スクリーンまでの\(d_2\)の範囲における光路長差\(\Delta l_2\)を求めます。 | |
 | 同じような計算かな。 \[ \begin{align*} \Delta l_2 &= \sqrt{ {d_2}^2 + \left( \frac{h}{2} + y \right)^2 } - \sqrt{ {d_2}^2 + \left( \frac{h}{2} - y \right)^2 } \\ &\fallingdotseq \left[ d_2 + \frac{1}{2 d_2} \left( \frac{h}{2} + y \right)^2 \right] - \left[ d_2 + \frac{1}{2 d_2} \left( \frac{h}{2} - y \right)^2 \right] \\ &= \frac{h y}{d_2} \tag{3.1.9} \end{align*} \] | |
 | 全体の位相差\(\Delta\phi\)は?? | |
 | こうですね。 \[ \Delta \phi = \frac{2 \pi}{\lambda} \left( \Delta l_1 + \Delta l_2 \right) = \frac{2 \pi}{\lambda} h \left( \frac{\delta}{d_1} + \frac{y}{d_2} \right) \tag{3.1.10} \] | |
 | そうすると、スクリーンの明線条件が分かります。 | |
 | 次数を\(m\)として、 \[ 2 m \pi = \frac{2 \pi}{\lambda} h \left( \frac{\delta}{d_1} + \frac{y}{d_2} \right) \quad \Leftrightarrow \quad m \lambda = h \left( \frac{\delta}{d_1} + \frac{y}{d_2} \right) \tag{3.1.11} \] ですね。 | |
 |
さて、\(0\)次の干渉縞に着目しましょう。このとき、\(m=0\)ですから、
\[
0 = h \left( \frac{\delta}{d_1} + \frac{y_0}{d_2} \right) \quad \Leftrightarrow \quad \frac{\delta}{d_1} = - \frac{y_0}{d_2} \tag{3.1.12}
\]
となります。これは、作図的には図3.1.4のように、光源Aと\(y_0\)を結ぶ線分Lは、スリットの真ん中を通過することを意味します。
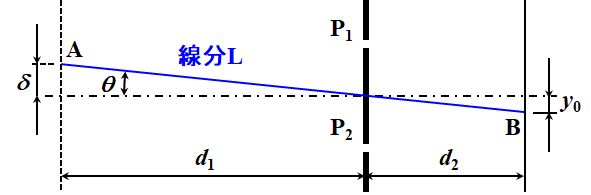 図3.1.4 Youngの干渉実験(2) よって、線分Lと中心線のなす角を\(\theta\)とすると、 \[ \frac{\delta}{d_1} = - \frac{y_0}{d_2} \fallingdotseq \theta \tag{3.1.13} \] が成立するのです。 |
〜天体干渉計〜
 | Youngの干渉実験(論文)って、どんな教科書でも最初に紹介されてますけど、歴史的意義だけ?? | |
 | そんなことないですよ。例えば、遠方にある2点間の距離を角度で表記する角距離という定義がありますが、これを求めるときに使ったりします。 | |
 | とすると、天体観測?? | |
 |
そうですね。ですから、このような干渉計は天体干渉計と言ったりします。
 図3.1.5 北斗七星の二重星 これは、北斗七星にある二重星の天体写真なんですが、この二重星の角距離を求める、とかね。 |
|
 | あ〜、その二重星って、昔アラビアで、徴兵の際の目の検査で使ってたやつですよね?? | |
 |
そうです。ちゃんと二重に見えれば合格という視力検査ですね。また、日本では不吉な星という伝説があり、『北斗の拳』では死期の近づいた者の頭上に輝くと表現されていました。
 図3.1.6 二重星=死兆星 |
|
 | マンガ…。 | |
 |
ここでは、簡単のため二重星の強度は同じ、そして中心線から\(\pm\delta\)だけ離れているとしておきましょう。
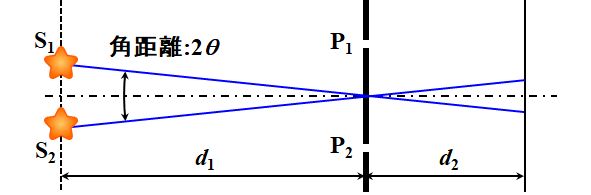 図3.1.7 角距離 そうすると、星S1の干渉項\(I_1\)は、 \[ I_1 = 2 A^2 \cos \left[ \frac{2 \pi}{\lambda} h \left( \frac{\delta}{d_1} + \frac{y}{d_2} \right) \right] \] 星S2の干渉項\(I_2\)は、 \[ I_2 = 2 A^2 \cos \left[ \frac{2 \pi}{\lambda} h \left( - \frac{\delta}{d_1} + \frac{y}{d_2} \right) \right] \] と書けます。 |
|
 | スクリーン上は、この2つの影響が重なって見えるから、 \[ \begin{align*} I_0 &= I_1 + I_2 \\ &= 2 A^2 \cos \left[ \frac{2 \pi}{\lambda} h \left( \frac{\delta}{d_1} + \frac{y}{d_2} \right) \right] + 2 A^2 \cos \left[ \frac{2 \pi}{\lambda} h \left( - \frac{\delta}{d_1} + \frac{y}{d_2} \right) \right] \\ &= 4 A^2 \cos \left( \frac{2 \pi}{\lambda} \frac{h\delta}{d_1} \right) \cos \left( \frac{2 \pi}{\lambda} \frac{hy}{d_2} \right) \\ &\fallingdotseq 4 A^2 \cos \left( \frac{2 \pi}{\lambda} h\theta \right) \cos \left( \frac{2 \pi}{\lambda} \frac{hy}{d_2} \right) \tag{3.1.14} \end{align*} \] ですね。 | |
 | 式3.1.14の2つ目の三角関数は、\(y\)に依存して振幅が周期的に変化する項なので、まさしく合成干渉縞を表しているんですが、特徴的なのは1つ目の三角関数で、これは出現した合成干渉縞のコントラストを決める項になります。 | |
 | \(h\)の関数になってますね。 | |
 | ということは、\(h\)を変化させるとコントラストが変化する、ということです。よって、\(h\)を\(0\)から徐々に大きくしていって、最初にコントラストが\(0\)になる\(h_1\)が求まると、 \[ \frac{\pi}{2} = \frac{2 \pi}{\lambda} h_1 \theta \quad \Leftrightarrow \quad 2 \theta = \frac{\lambda}{2 h_1} \tag{3.1.15} \] として、角距離が求まるわけです。 | |
 | Youngの干渉実験って、意外と実用的なんですねぇ。 |
| 前頁へ | 戻る | 次頁へ |