 | 干渉の具体例の2つ目はNewton環です。 | |
 |
これですね。
 図3.1.8 Newton環 |
|
 |
教科書を見ると、リファレンスは平板ガラスとしているものが殆どですが、レンズ加工の現場では原器と呼ばれるお皿を使って評価します。
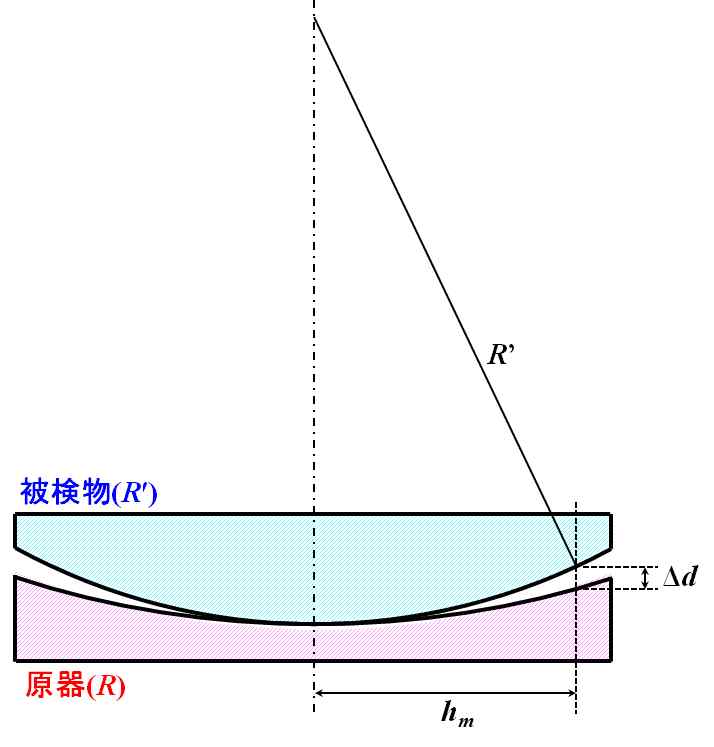 図3.1.9 Newton環の原理(\(R^{\thinspace \prime} < R\)) |
|
 | 前にやりましたね。 | |
 |
図3.1.9は、被検物の曲率半径(\(R^{\thinspace \prime}\))の方が原器の曲率半径(\(R\))よりも小さい場合ですが、ここでは少し汎用性を持たせるために、逆のケースで復習してみましょう。
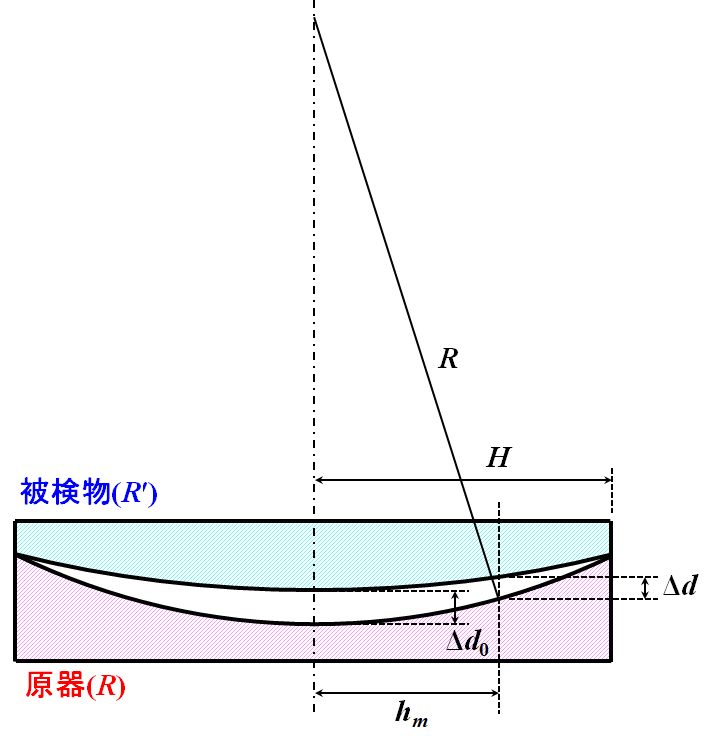 図3.1.10 Newton環の原理(\(R^{\thinspace\prime} > R\)) このとき、中心における隙間を\(\Delta d_0\)、被検物と原器の接点〜中心までの距離を\(H\)と置くと、 \[ \Delta d_0 + \left( R^{\thinspace\prime} - \sqrt{ R^{\thinspace\prime \thinspace 2} - H^2} \right) - \left(R - \sqrt{ R^2 - H^2} \right) = 0 \tag{3.1.16} \] が成立します。任意の\(h_m\)における光路長差\(\Delta d\)はどう表せますか?? |
|
 | う〜ん。 \[ \Delta d_0 + \left( R^{\thinspace \prime} - \sqrt{ R^{\thinspace \prime \thinspace 2} - {h_m}^2} \right) - \left(R - \sqrt{ R^2 - {h_m}^2} \right) = \Delta d \tag{3.1.17} \] ですね。 | |
 | 式3.1.17から式3.1.16を引いてください。 | |
 | えいっ!! \[ \begin{align*} \Delta d &= \left( \sqrt{ R^{\thinspace \prime \thinspace 2} - H^2} - \sqrt{ R^{\thinspace \prime \thinspace 2} - {h_m}^2} \right) - \left(\sqrt{ R^2 - H^2} - \sqrt{ R^2 - {h_m}^2} \right) \\ &= \left\{ R^{\thinspace \prime} \sqrt{ 1 - \left( \frac{H}{R^{\thinspace \prime}} \right)^2 } - R^{\thinspace \prime} \sqrt{ 1 - \left( \frac{h_m}{R^{\thinspace \prime}} \right)^2 } \right\} \\ & \quad \quad \quad \quad - \left\{ R \sqrt{ 1 - \left( \frac{H}{R} \right)^2 } - R \sqrt{ 1 - \left( \frac{h_m}{R} \right)^2 } \right\} \\ &\fallingdotseq \left( R^{\thinspace \prime} - \frac{H^2}{2R^{\thinspace \prime}} - R^{\thinspace \prime} + \frac{{h_m}^2}{2R^{\thinspace \prime}} \right) - \left( R - \frac{H^2}{2R} - R + \frac{{h_m}^2}{2R} \right) \\ &= \frac{{h_m}^2 - H^2}{2R^{\thinspace \prime}} - \frac{{h_m}^2 - H^2}{2R} = \frac{{h_m}^2 - H^2 }{2} \left( \frac{1}{R^{\thinspace \prime}} - \frac{1}{R} \right) \tag{3.1.18} \end{align*} \] | |
 | そうすると、位相差\(\Delta\phi\)が求まります。 | |
 | こうですね。 \[ \Delta \phi = \frac{2 \pi}{\lambda} \times 2 \Delta d = \frac{2 \pi}{\lambda} \left( {h_m}^2 - H^2 \right) \left( \frac{1}{R^{\thinspace \prime}} - \frac{1}{R} \right) \tag{3.1.19} \] | |
 | 式3.1.19から明暗条件が決定されますが、注意しなければならないのは、原器での反射は固定端の扱いになるので、位相が反転するということです。従って、縞の見える(弱め合う干渉)条件は、 \[ \begin{align*} &2 m \pi = \frac{2 \pi}{\lambda} \left( {h_m}^2 - H^2 \right) \left( \frac{1}{R^{\thinspace \prime}} - \frac{1}{R} \right) \\ &\Leftrightarrow \quad m \lambda = \left( {h_m}^2 - H^2 \right) \left( \frac{1}{R^{\thinspace \prime}} - \frac{1}{R} \right) \tag{3.1.20} \end{align*} \] となります。 | |
 | \(R^{\thinspace \prime} < R\)だと、\(H=0\)だから、 \[ m \lambda = {h_m}^2 \left( \frac{1}{R^{\thinspace \prime}} - \frac{1}{R} \right) \tag{3.1.21} \] だけど、前にやった結果とは違いますね(\(\Delta R=R-R^{\thinspace \prime}>0\))。 \[ m \lambda = 2 \Delta R \left\{ 1- \sqrt{ 1 - \left( \frac{h_m}{R} \right)^2 } \right\} \tag{3.1.22} \] | |
 | それは近似するときの着眼点が異なるからですね。式3.1.22の右辺は、 \[ 2 \Delta R \left\{ 1- \sqrt{ 1 - \left( \frac{h_m}{R} \right)^2 } \right\} \fallingdotseq 2 \Delta R \left(1- 1 + \frac{{h_m}^2}{2R^2} \right) = \frac{{h_m}^2}{R^2} \Delta R \] にまで近似できますし、式3.1.21の右辺は、 \[ {h_m}^2 \left( \frac{1}{R^{\thinspace \prime}} - \frac{1}{R} \right) = \frac{{h_m}^2}{R^{\thinspace \prime}R} \left(R-R^{\thinspace \prime}\right) \fallingdotseq \frac{{h_m}^2}{R^2} \Delta R \] と近似できるので、2つの式はほぼ等価と言うことができます。 | |
 | \(R^{\thinspace \prime} < R\)の場合は、式3.1.21から、\(m=0\)のとき\(h_0=0\)だから、中心付近は必ず暗部になるわけですね。 | |
 | そうです。 | |
 | \(R^{\thinspace \prime}>R\)の場合、中心付近の明暗は、\(\Delta R=R^{\thinspace \prime}-R\left(>0\right)\)の大きさで違ってきそうですね。 | |
 | 式3.1.20によれば、\(h_m=0\)のとき、 \[ m \lambda = H^2 \left( \frac{1}{R} - \frac{1}{R^{\thinspace \prime}} \right) = \frac{H^2}{R^{\thinspace \prime}R} \left( R^{\thinspace \prime} - R \right) \fallingdotseq \frac{H^2}{R^2} \Delta R \tag{3.1.23} \] ですから、式3.1.23を満たす\(\Delta R\)のときに中心付近が暗部になります。 | |
 | あ、そっか。\(R^{\thinspace \prime}>R\)の場合は、\(m=0\)の輪帯は中心ではなくて、被検物と原器の接している付近(\(h_0=H\))になるわけだ…。 | |
 | そこは注意しないといけませんね。 | |
 | でも、式3.1.23を満たしたときは、\(R^{\thinspace \prime}> R\)でも\(R^{\thinspace \prime}< R\)でも中心付近は暗部だから、見分けがつかないですね。 | |
 |
その場合は、被検物の中心をちょっとだけ押してやります。\(R^{\thinspace \prime}< R\)のときは、\(R^{\thinspace \prime}\)は\(R\)に近づくにつれて\(R^{\thinspace \prime}\)→大なので、 \(R^{\thinspace \prime}\)→大 ⇒ \(\cfrac{1}{R^{\thinspace \prime}}\)→小 ⇒ \(\cfrac{1}{R^{\thinspace \prime}}-\cfrac{1}{R}\)→小 となり、ある輪帯\(h_m\)に注目すると、式3.1.21より\(h_m\)→大ですから、あたかも輪帯は中心から湧き出して広がるように観察されます。 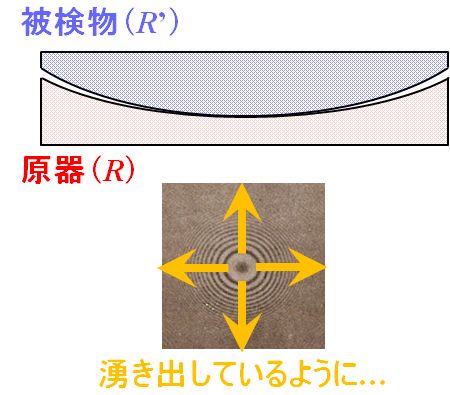 図3.1.11 \(R^{\thinspace \prime}< R\)のとき 一方、\(R^{\thinspace \prime}> R\)のときは、\(R^{\thinspace \prime}\)は\(R\)に近づくにつれて\(R^{\thinspace \prime}\)→小なので、 \(R^{\thinspace \prime}\)→小 ⇒ \(\cfrac{1}{R^{\thinspace \prime}}\)→大 ⇒ \(\cfrac{1}{R^{\thinspace \prime}}-\cfrac{1}{R}\)→大 となり、ある輪帯\(h_m\)に注目すると、式3.1.20より\(h_m\)→小ですから、あたかも輪帯は中心に吸い込まれるように観察されます。 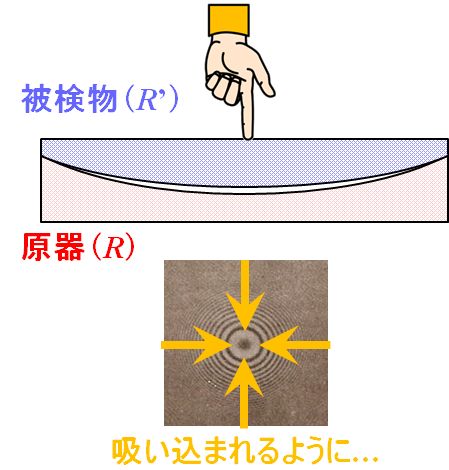 図3.1.12 \(R^{\thinspace \prime}> R\)のとき |
|
 | う〜ん。理屈は分かるけど、あんまり被検物は触りたくないですよね?? | |
 | なので、例えばレンズの表面形状公差に±3ニュートンと記載があったら、原器の方をわざと設計値からニュートン3本分ずらして加工し、0〜6本まではOKというような検査をするのが一般的です。 |
〜小数のNewton環〜
 |
教授。この図面なんですけど。
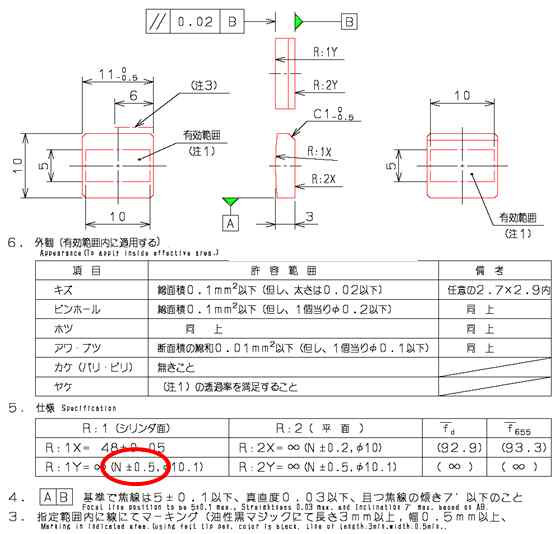 図3.1.13 シリンドリカル・レンズの図面 |
|
 | シリンドリカル・レンズですね。 | |
 | ニュートン本数のところを見ると、0.5本とかって書かれているんですけど、5本の間違いですよね?? | |
 | いや、間違いじゃないでしょう。 | |
 | でも、本数って整数で数えますよ。そもそも、縞の見える条件の\(m\)って整数じゃないですか。 | |
 |
図3.1.14のような場合、どっちも\(m=1\)ですが、明らかに被検物の\(R^{\thinspace \prime}\)は同じではないですよね??
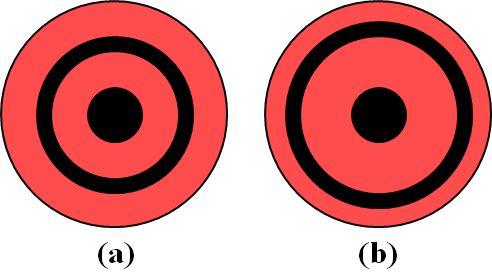 図3.1.14 どちらも\(m=1\) |
|
 | ムムム。それは、そうですね…。 | |
 | なので、この違いをニュートン本数で表現するときに、小数を使うわけです。 | |
 | う〜ん。でも、(a)と(b)のどっちが\(m=1.5\)かは分からないですよ。 | |
 |
1つの解決方法としては、図面に記載のニュートン本数を曲率半径に換算して、触針式のForm Talysurfで評価する方法があります。
 図3.1.15 Form Talysurf |
|
 | ん〜。でも、その方法だと、レンズ表面のすべては評価できないし、量産向きじゃないですよね。 | |
 | 確かに、Newton環を用いた方法でテキパキやりたいですね。 | |
 | 何か解決方法がありますか?? | |
 |
\(R^{\thinspace \prime}< R\)であれば、ワザがあります。原器に被検物を重ねるとき、お互いの中心を少しだけずらしてやるんです。そうすると、Newton環がこんなふうに観察されます。
 図3.1.16 中心からずれたNewton環 |
|
 | 中心がずれているんだから、当然ですよね。 | |
 |
こうしておいて、1本の干渉縞に着目し、その反り具合\(u\)を測ります。次に縞の間隔\(s\)を測る。そして、その割り算を計算すると、ニュートン本数が得られます。
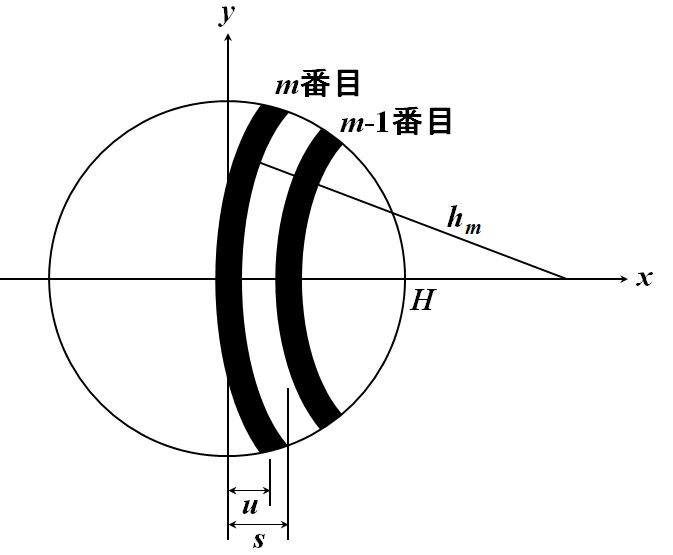 図3.1.17 新手法でのNewton環 |
|
 | え〜。直感的には理解できないですけど…。 | |
 | 証明するのは、そんなに難しくないです。まず、図3.1.17において、有効径の半径を\(H\)とすると、その境界線は、 \[ x^2 + y^2 = H^2 \tag{3.1.24} \] ですし、\(m\)番目の縞は、 \[ \left( x - h_m \right)^2 + y^2 = {h_m}^2 \tag{3.1.25} \] と書けます。 | |
 | はい。 | |
 | 一方、\(R^{\thinspace \prime}< R\)のときは式3.1.21が成立しますが、 \[ C \equiv \frac{\cfrac{1}{R^{\thinspace \prime}} - \cfrac{1}{R} }{\lambda} \tag{3.1.26} \] としておきましょう。 | |
 | そうすると、式3.1.21は、 \[ m = {h_m}^2 C \tag{3.1.27} \] ですね。 | |
 | ここから、\(s\)を求めます。 | |
 | \(s\)は縞の間隔か…。 \[ s = h_m - h_{m-1} = \sqrt{\frac{m}{C}} - \sqrt{\frac{m-1}{C}} \tag{3.1.28} \] かな。 | |
 | 一方、\(u\)は式3.1.24と式3.1.25の交点の\(x\)座標として与えられます。 | |
 | ということは、式3.1.24から式3.1.25を引けば計算できそうですね。 \[ 2 h_m u - {h_m}^2 = H^2 - {h_m}^2 \Leftrightarrow u = \frac{H^2}{2h_m} \tag{3.1.29} \] かな。 | |
 | ここで、境界線\(H\)における次数を\(M\)(小数)と置けば、式3.1.27から、 \[ M = H^2 C \tag{3.1.30} \] が成立するはずです。そうすると、式3.1.29はどうなりますか?? | |
 | え〜と、 \[ u = \frac{H^2}{2h_m} = \frac{\cfrac{M}{C}}{2\sqrt{\cfrac{m}{C}}} \tag{3.1.31} \] ですね。 | |
 | では、式3.1.31を式3.1.28で割ってみましょう。 | |
 | それで\(\cfrac{u}{s}\)が求まるのか…。 \[ \begin{align*} \frac{u}{s} &= \frac{\cfrac{M}{C}}{2\sqrt{\cfrac{m}{C}}} \div \left( \sqrt{\frac{m}{C}} - \sqrt{\frac{m-1}{C}} \right) \\ &= \frac{M}{2C} \div \left( \frac{m}{C} - \frac{ \sqrt{\left(m-1 \right) m}}{C} \right) = \frac{M}{2 \left( m - m \sqrt{ 1 - \cfrac{1}{m} } \right) } \end{align*} \] | |
 | 分母の第2項は、 \[ m \sqrt{ 1 - \frac{1}{m} } \fallingdotseq m \left( 1 - \frac{1}{2m} \right) = m - \frac{1}{2} \] と近似できますね。 | |
 | そうすると、 \[ \frac{u}{s} \fallingdotseq M \tag{3.1.32} \] で、次数が\(\cfrac{u}{s}\)と一致しました〜。 | |
 | 計算としては、かなり乱暴な近似を行ってますが、この方法であれば目分量でも小数のニュートン本数を評価できますし、簡便なので現場ではよく使われてますね。 |
| 前頁へ | 戻る | 次頁へ |