 |
干渉の具体例の3つ目はMichelson-Morleyの干渉実験です。
 Albert Abraham Michelson(1852〜1931) |
|
 | あ〜、予告してましたもんね。 | |
 |
Michelsonが用いたのは、Michelson干渉計と呼ばれる装置です。
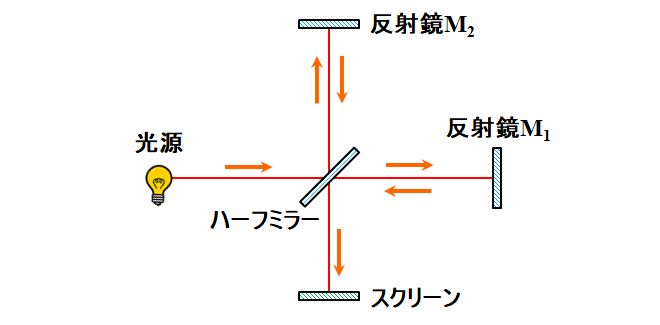 図3.1.18 Michelson干渉計 まず、ハーフミラーで光を2つに分け、1つを参照波面、もう1つを被検物を透過する波面とし、それらを同じハーフミラーで重ね合わせて干渉させるというのが基本原理(論文)です。 |
|
 | いろいろなタイプの干渉計があるんですねぇ。でも、この場合の被検物って?? | |
 | もちろん、エーテルですよ。 | |
 | これで、エーテルの有無が証明できるんですか?? | |
 | Michelsonのアイデアは、次のようなものです。もし、エーテルが存在し、その中を地球が泳いでいるとすれば、ある種の抵抗を感じるに違いありません。これをエーテル風と言いますが、地球は自転/公転しているので、エーテル風の影響は時々刻々と変化していると予想されます。 | |
 | その変化を捉えられれば、エーテルの存在証明ができるってことかぁ。 | |
 |
例えば、図3.1.19のように、地球とともに速度\(v\)で運動している干渉計を考えましょう。
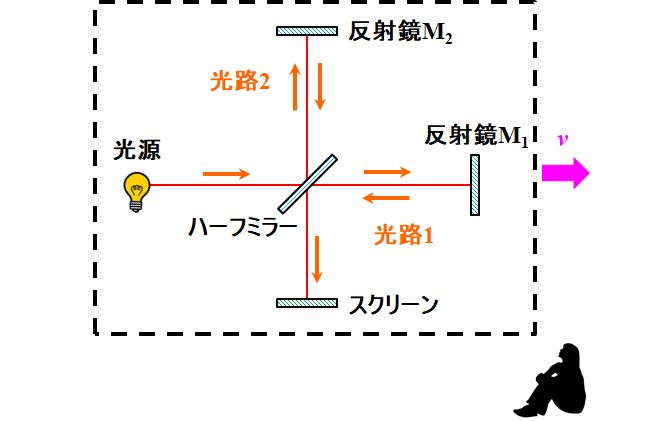 図3.1.19 エーテルの存在証明:\(0^{\circ}\)のとき そのとき、エーテル座標系(絶対座標系)から見たら、干渉計のすべての部品は速度\(v\)で運動しているので、光路1について、光路長は\(2D_1\)で不変です。 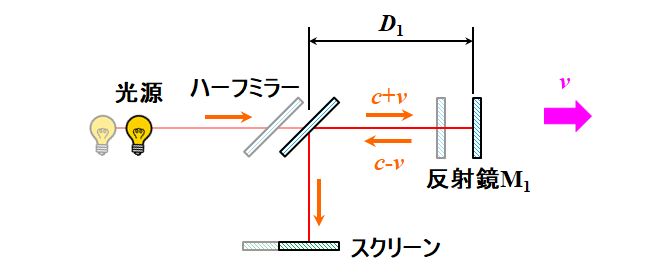 図3.1.20 エーテルの存在証明:\(0^{\circ}\)のときの光路1 しかし、古典力学の立場で考えると、ハーフミラーから反射鏡M1まで伝搬する光速は\(c+v\)ですし、反射鏡M1からハーフミラーまで伝搬する光速は\(c-v\)で異なります。よって、ハーフミラー〜反射鏡M1の往復時間を\(t_1\)とすれば、\(\beta \equiv \cfrac{v}{c}\)として、 \[ t_1 = \frac{D_1}{c+v} + \frac{D_1}{c-v} = \frac{2c}{c^2-v^2}D_1 \quad \Leftrightarrow \quad c t_1 = \frac{2c^2}{c^2 - v^2 }D_1 = \frac{2D_1}{1 - \beta^2 } \tag{3.1.33} \] と書けます。 |
|
 |
光路2は、エーテル座標系からは図3.1.21のように見えるから、
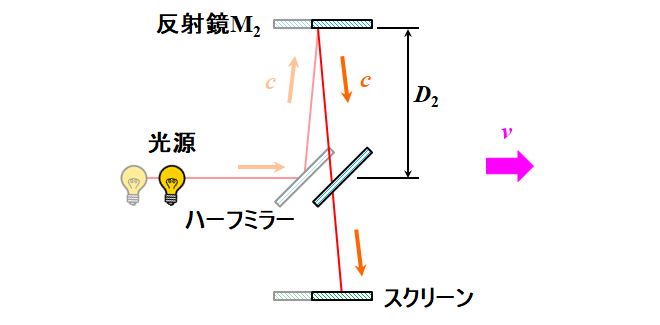 図3.1.21 エーテルの存在証明:\(0^{\circ}\)のときの光路2 ハーフミラー〜反射鏡M2の往復時間を\(t_2\)とすると、Pythagorasの定理から、 \[ \begin{align*} &\left( \frac{c t_2}{2} \right)^2 = {D_2}^2 + \left( \frac{v t_2}{2} \right)^2 \quad \Leftrightarrow \quad \left( {c t_2} \right)^2 \left( 1 - \frac{v^2}{c^2} \right) = \left( {2 D_2} \right)^2 \\ &\Leftrightarrow \quad c t_2 = \frac{2 D_2}{\sqrt{1 - \beta^2}} \tag{3.1.34} \end{align*} \] ですね。 |
|
 | そうすると、光路長差\(\Delta D\)が求まりますね?? | |
 | 式3.1.33から式3.1.34を引けばいいかな。 \[ \Delta D = c t_1 - c t_2 = \frac{2D_1}{1 - \beta^2} - \frac{2 D_2}{\sqrt{1 - \beta^2}} \tag{3.1.35} \] | |
 |
次に、図3.1.19を基準にして、装置が\(90^{\circ}\)回転したとしましょう。
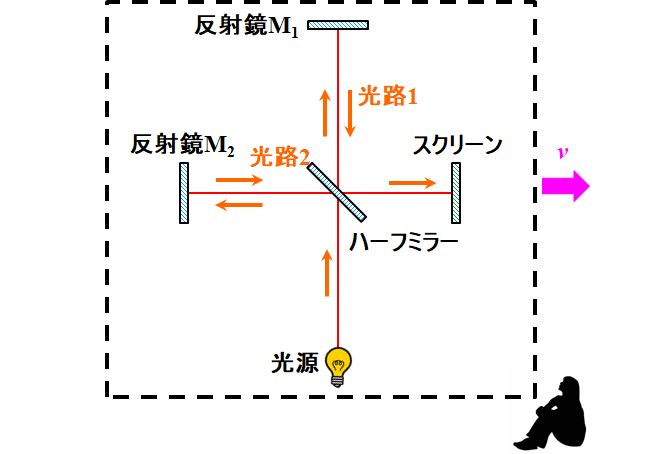 図3.1.22 エーテルの存在証明:\(90^{\circ}\)のとき |
|
 |
光路2については、さっきの光路1と同じ理屈が成立しそうですね。エーテル座標系から見たら、光路長は\(2D_2\)で不変。
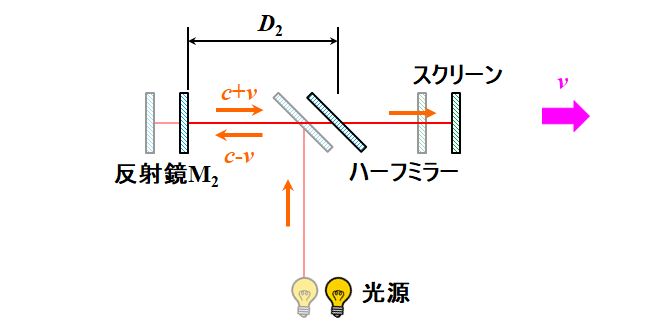 図3.1.23 エーテルの存在証明:\(90^{\circ}\)のときの光路2 ハーフミラーから反射鏡M2まで伝搬する光速は\(c-v\)、反射鏡M2からハーフミラーまで伝搬する光速は\(c+v\)だから、ハーフミラー〜反射鏡M2の往復時間を\({t_2}^{\prime}\)とすれば、 \[ {t_2}^{\prime} = \frac{D_2}{c+v} + \frac{D_2}{c-v} = \frac{2c}{c^2-v^2}D_2 \quad \Leftrightarrow \quad c {t_2}^{\prime} = \frac{2c^2}{c^2 - v^2 }D_2 = \frac{2D_2}{1 - \beta^2 } \tag{3.1.36} \] ですね。 |
|
 |
光路1は、エーテル座標系からは図3.1.24のように見えるので、
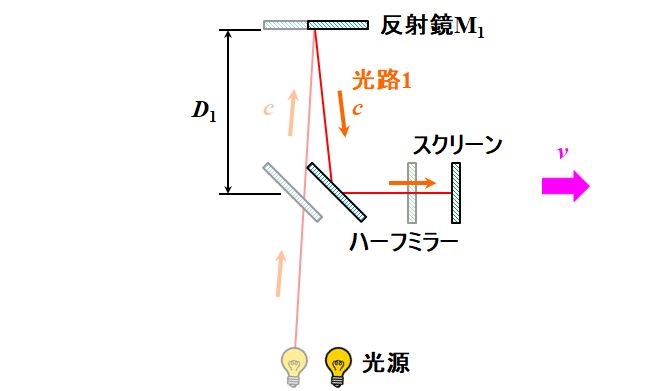 図3.1.24 エーテルの存在証明:\(90^{\circ}\)のときの光路1 ハーフミラー〜反射鏡M1の往復時間を\({t_1}^{\prime}\)とすると、Pythagorasの定理から、 \[ \begin{align*} &\left( \frac{c {t_1}^{\prime}}{2} \right)^2 = {D_1}^2 + \left( \frac{v {t_1}^{\prime}}{2} \right)^2 \quad \Leftrightarrow \quad \left( {c {t_1}^{\prime}} \right)^2 \left( 1 - \frac{v^2}{c^2} \right) = \left( {2 D_1} \right)^2 \\ &\Leftrightarrow \quad c {t_1}^{\prime} = \frac{2 D_1}{\sqrt{1 - \beta^2}} \tag{3.1.37} \end{align*} \] となります。 |
|
 | で、光路長差\(\Delta D^{\thinspace \prime}\)を求めるわけか…。 \[ \Delta D^{\thinspace \prime} = c {t_1}^{\prime} - c {t_2}^{\prime} = \frac{2D_1}{\sqrt{1 - \beta^2}} - \frac{2 D_2}{1 - \beta^2} \tag{3.1.38} \] | |
 | \(D_1\)と\(D_2\)がほぼ等しい(\(D_1\fallingdotseq D_2=D\))とすれば、\(\Delta D\)(式3.1.35)と\(\Delta D^{\thinspace \prime}\)(式3.1.38)を比較したとき、どっちの方が大きいですか?? | |
 | \(\beta^2\)は\(1\)より小さいから…。\(\Delta D\)の方が大きいんじゃないですか?? | |
 | とすれば、図3.1.19のレイアウトを基準にして、このときに光路長差は\(\Delta D\)で最大となり、\(90^{\circ}\)回転した図3.1.22のときに光路長差は\(\Delta D^{\thinspace \prime}\)で最小となり、更に\(90^{\circ}\)回転すると再び光路長差は\(\Delta D\)で最大になる、というように、干渉計をグルグル回転させると、光路長差は三角関数のような変化を示すだろうな、という予測が立ちます。さて、その振れ幅はいくつでしょう?? | |
 | 振幅じゃなくて振れ幅か…。 \[ \begin{align*} \Delta D - \Delta D^{\thinspace \prime} &= \left( \frac{2D_1}{1 - \beta^2} - \frac{2 D_2}{\sqrt{1 - \beta^2}} \right) - \left( \frac{2D_1}{\sqrt{1 - \beta^2}} - \frac{2 D_2}{1 - \beta^2} \right) \\ &= \frac{2 \left( D_1 + D_2 \right)}{1 - \beta^2} - \frac{2 \left( D_1 + D_2 \right)}{\sqrt{1 - \beta^2}} \\ &= 2 \left( D_1 + D_2 \right) \left( \frac{1}{1 - \beta^2} - \frac{1}{\sqrt{1 - \beta^2}} \right) \\ &\approx 2 \left( D_1 + D_2 \right) \left[ \left( 1 + \beta^2 \right) - \left( 1 + \frac{\beta^2}{2} \right) \right] = \left( D_1 + D_2 \right)\beta^2 \end{align*} \] \[ \phantom{c \left( \Delta t - \Delta t^{\prime} \right)}\approx 2D\frac{ v^2}{c^2} \tag{3.1.39} \] | |
 |
これが、論文の数式になります。
 図3.1.25 論文抜粋(1) |
|
 | 式3.1.39って、どのくらいの大きさなんだろ?? | |
 | 論文によれば、\(D\)=11m。地球の公転速度は28km/sですが、約30km/sと考えると計算しやすいです。 | |
 |
ということは、 2 × 11 m × ( 30×103 m/s ÷ 3×108 m/s )2 = 220 nm か。可視光の波長が550nm程度だとすると、波長の約0.4倍の変化ってことですね。 |
|
 | その数字も論文に書かれてますよね?? | |
 | う〜ん、でも論文は干渉縞ピッチ(fringe)の0.4倍って書かれてますけど?? | |
 | 光路長差の変化量を\(\lambda\)で割ったものと、干渉縞の変位量(displacement)を干渉縞ピッチ(fringe)で割ったものは同じだから、論文の表現で問題ないですよ。 | |
 | いまいち納得できないなぁ。 | |
 |
例えば、Youngの干渉実験を思い出してください。
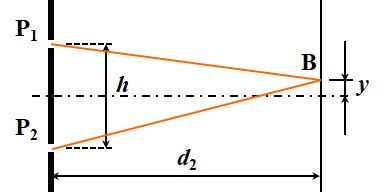 図3.1.26 Youngの干渉実験再び 簡単のため、\(d_2\)の範囲だけで考えると、光路長差は式3.1.9でしたね。 \[ \Delta l_2 = \frac{h y}{d_2} \tag{3.1.9} \] ここで注意すべきは、Youngの干渉実験ではスリットP1とP2の位相は揃っていると勝手に仮定していた、ということです。しかし、Michelson-Morleyの干渉実験は、ここに時間とともに変化する光路長差\(\Delta l\left(t\right)\)が新たに加わっていると考えられます。つまり、 \[ \Delta l_2 = \frac{h y}{d_2} + \Delta l \left( t \right) \tag{3.1.40} \] よって、明線条件は、式3.1.11を参考にすると、 \[ m \lambda = h \frac{y}{d_2} + \Delta l \left( t \right) \tag{3.1.41} \] となります。さて、干渉縞ピッチ\(\Delta y\)はどのように書けますか?? |
|
 | う〜ん。\(m\)番目の縞と\(m+1\)番目の縞の間隔だから、 \[ \lambda = h \frac{\Delta y}{d_2} \quad \Leftrightarrow \quad \frac{h}{d_2} = \frac{\lambda}{\Delta y} \tag{3.1.42} \] じゃないかな。 | |
 | では、光路長差が\(\Delta l\left(t_1\right)\)から\(\Delta l\left(t_2\right)\)に変化したとき、縞の位置はどう変化するでしょう?? | |
 | それは、 \[ m \lambda = h \frac{y_1}{d_2} + \Delta l \left( t_1 \right) \] と、 \[ m \lambda = h \frac{y_2}{d_2} + \Delta l \left( t_2 \right) \] とを引けばいいから、 \[ h \frac{y_2-y_1}{d_2} = \Delta l \left( t_1 \right) - \Delta l \left( t_2 \right) \quad \Leftrightarrow \quad \frac{h}{d_2} = \frac{\Delta l \left( t_1 \right) - \Delta l \left( t_2 \right)}{y_2-y_1} \tag{3.1.43} \] かな。 | |
 | 式3.1.42と式3.1.43から、 \[ \frac{\lambda}{\Delta y} = \frac{\Delta l \left( t_1 \right) - \Delta l \left( t_2 \right)}{y_2-y_1} \quad \Leftrightarrow \quad \frac{y_2-y_1}{\Delta y} = \frac{\Delta l \left( t_1 \right) - \Delta l \left( t_2 \right)}{\lambda} \tag{3.1.44} \] つまり、光路長差の変化量:\(\Delta l\left(t_1\right)-\Delta l\left(t_2\right)\)を\(\lambda\)で割ったものと、干渉縞の変位量:\(y_2-y_1\)を干渉縞ピッチ:\(\Delta y\)で割ったものが等しいことが導けました。 | |
 | なるほど。 | |
 |
では、Michelsonらの実測データから、光路長差の変化量が\(0.4\lambda\)だったかトレースしてみましょう。まず、彼らは干渉縞ピッチと、マイクロメータのネジの読み値との関係から、ネジの1目盛が\(0.02\lambda\)であることを割り出します。
 図3.1.27 論文抜粋(2) そして、データリストがこれです。 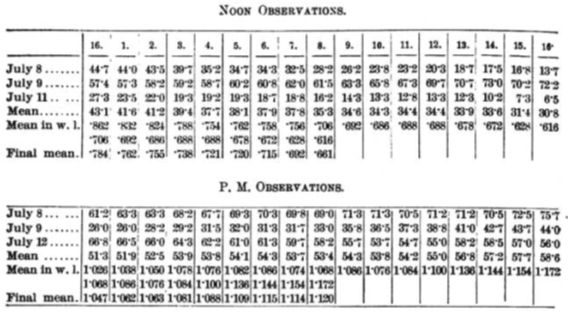 図3.1.28 論文抜粋(3) |
|
 | 7/8、9、11のお昼と午後6時のデータですね。横軸の1〜16は何だろう?? | |
 |
それは、方位を16等分して番号を振ったものです。
 図3.1.29 論文抜粋(4) |
|
 | ということは、さっきの教授の説明だと、ちょうど点対称の位置にあるデータは、理屈上は同じになってないとおかしいですよね。 | |
 |
そうですね。ですから、図3.1.28のデータをよく見ると、下から3行目の右半分のデータが、そのまま下から2行目にスライドされてますよね??
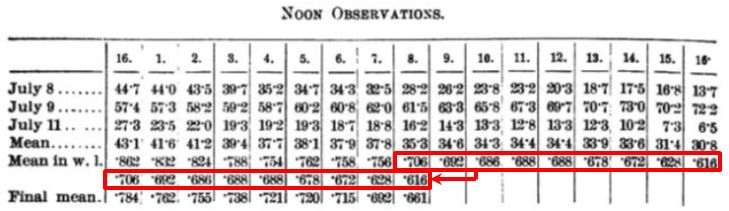 図3.1.30 論文抜粋(5) |
|
 | あ、本当だ。下から3行目と2行目の平均が一番下(Final Mean)の結果になっているのかぁ。 | |
 | 上の4行(July 8〜Mean)は、ネジの目盛(=光路長差)がそのまま記録されています。4行目(Mean)は、7/8、9、11の3日間の平均値。これに、\(0.02\lambda\)を掛けたのが5行目(下から3行目)になります。 | |
 |
う〜ん。グラフにしてみたけど…。
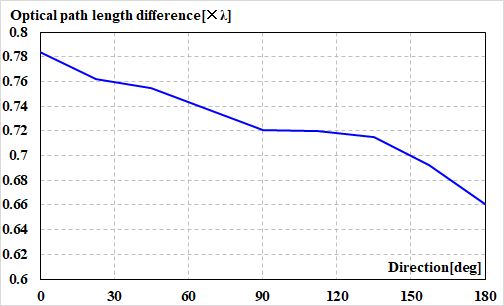 図3.1.31 正午の光路長差の変化 何だかよく分からないですね…。 |
|
 |
まず、グラフが緩やかに右肩下がりになってますが、この測定は非常に繊細であるために、例えば温度がジワジワと変化するだけで装置に微小な変形を引き起こし、その影響が測定結果に出ている可能性があります。
 図3.1.32 論文抜粋(6) なので、そういうノイズを除去するための補正が必要なんですよ。 |
|
 | どう補正するのが適切ですか?? | |
 | 少なくとも、\(180^{\circ}\)回転させたら結果は同じになるだろうと思われるので、\(0^{\circ}\)と\(180^{\circ}\)のデータを結んで、その直線の分を差し引くのが妥当でしょうね。 | |
 |
補正データと理論値(破線)を重ねると、こんな感じか。
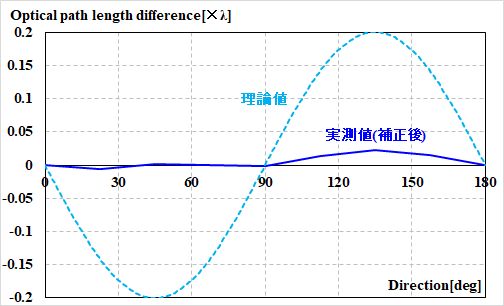 図3.1.33 正午の光路長差の変化(補正データ) 実測値がペシャンコになっちゃいましたよ。 |
|
 | つまり、\(0.4\lambda\)の変化を示すべきところが、殆ど変化しなかった、ということですね。 | |
 | エーテル風なんて吹いてない、ってことか…。 | |
 | 同じように午後6時のデータはどうですか?? | |
 |
夕方も代り映えしないですね。
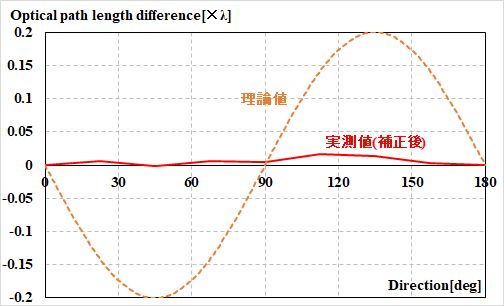 図3.1.34 夕方の光路長差の変化(補正データ) |
|
 |
ですから、論文では理論値を1/8倍して実測データの変化を見やすく工夫してますが、それでもペシャンコに見えるので、「実際の変位はこの値(=理論値)の1/20よりも間違いなく小さく、多分1/40よりも小さいであろう」と結論するわけです。
 図3.1.35 論文抜粋(7) |
|
 | この論文、なかなかのインパクトですよね?? | |
 |
そうですね。ですから、LorentzやFitzgeraldのように、この論文の結果と辻褄が合うようにエーテルの性質を練り直す(論文)学派が登場します。
 George Francis FitzGerald(1851〜1901) 一方で、Millerのように、この論文の実測を追試する(論文)動きも出てきます。  Dayton Clarence Miller(1866〜1941) もちろん、エーテルの存在を疑っていたMachのような物理学者は、この論文こそエーテルを否定する証拠であるとして支持します。Einsteinもその一人と考えていいでしょう。  Ernst Waldfried Josef Wenzel Mach(1838〜1916) |
|
 | 追試の結果は?? | |
 | すべてMichelson-Morleyを支持するものでした。 | |
 | そうかぁ。それで二人はノーベル物理学賞を受賞するわけですね。 | |
 | いえ、ノーベル賞はMichelsonだけですよ。 | |
 | ん??何で?? | |
 |
Morleyはあくまで助手です。干渉実験でエーテルの存在を証明するアイデアは1881年にMichelsonが提示済みなんですよ。ところが、そのときの測定は精度がよくなく、エーテルが存在しないと結論するには、ちょっと決め手に欠けていたので、装置を改良しリトライしたのが、この論文ということなのです。
 Edward Williams Morley(1838〜1923) |
|
 | ふ〜ん。お手伝いしただけでは、ノーベル賞はもらえないわけですね。 | |
 | Michelsonは非常に神経質な人で、MorleyはMichelsonのことをかなり付き合いにくい相手と考えていたそうですね。尤も、そういう人だからこそ、こういう緻密で繊細な測定に向いていたのかもしれませんがね。 |
| 前頁へ | 戻る | 次頁へ |