 | 薄膜干渉ってことは、シャボン玉みたいなやつですか?? | |
 |
いえ。ここで議論の対象とするのは、コーティングに繋がる理論です。
 図3.2.1 コーティング |
|
 | 教授のしている眼鏡みたいな話?? | |
 | そうですね。尤も、いまどきはコーティングもいろいろな設計ツールがありますし、ここでは基礎ということで簡単な例を扱うことにしましょう。 | |
 | 簡単??本当かな…。 | |
 |
というわけで、単層コートを題材にします。
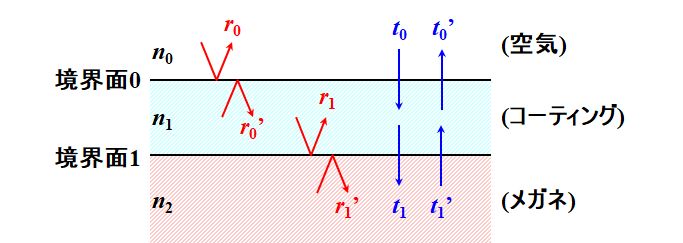 図3.2.2 Fresnel係数の定義 つまり、屈折率\(n_2\)の基板の上に、屈折率\(n_1\)のコート材を塗布し、屈折率\(n_0\)の環境下で光を透過させるというモデルですね。 |
|
 | 境界面は2つだけ、ってことか。 | |
 |
ところが、2つの境界面で屈折と反射は1度だけ起こるわけではなく、図3.2.3のように何度も繰り返されることに要注意です。
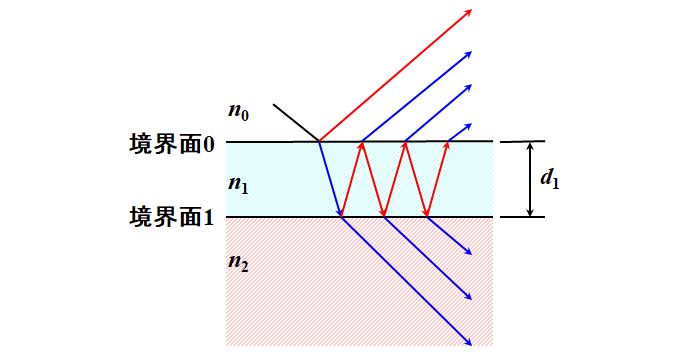 図3.2.3 実は多重反射している… |
|
 | え〜、やっぱり簡単じゃな〜い。 | |
 | では、もう1つ、光は垂直入射するという限定も加えましょう。 | |
 | それ、あんまり譲歩になってませんけど…。 | |
 |
境界面は2つですから、それぞれでFresnel反射率\(r\)とFresnel透過率\(t\)を定義することができます。境界面0の反射と透過を1回目と数えると、このときのFresnel反射率は\(r^{\left(1\right)}=r_0\)、Fresnel透過率は\(t^{\left(1\right)}=t_0\)です。
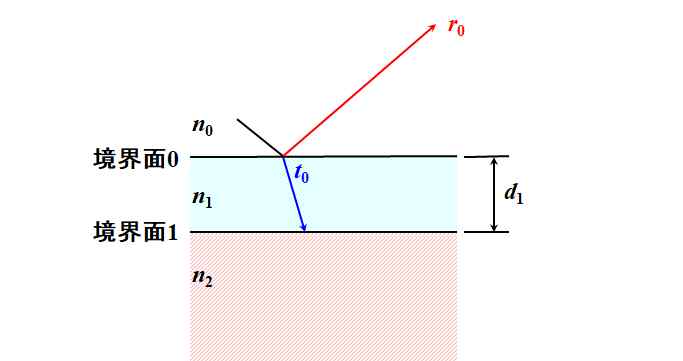 図3.2.4 1回目の反射と透過 次は境界面1で2回目の反射と透過が起こりますが、Fresnel反射率\(r^{\left(2\right)}\)、Fresnel透過率\(t^{\left(2\right)}\)はどう書けますか?? |
|
 | う〜ん。\(r^{\left(2\right)}=t_0 r_1\)、\(t^{\left(2\right)}=t_0 t_1\)かなぁ。 | |
 |
しかし、膜厚\(d\)に対応した位相差(\(\delta_1\))も考慮しないといけない。と言うわけで、\(r^{\left(2\right)}=t_0 r_1\exp\left(i\delta_1\right)\)、\(t^{\left(2\right)}=t_0 t_1\exp\left(i\delta_1\right)\)が正解ですね。
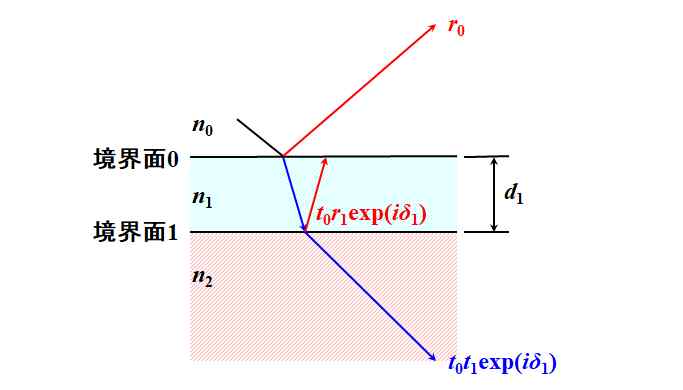 図3.2.5 2回目の反射と透過 |
|
 |
そうすると、3回目(境界面0)のFresnel反射率は\(r^{\left(3\right)}=t_0 {r_0}^{\prime} r_1\exp\left(2i\delta_1\right)\)、Fresnel透過率は\(t^{\left(3\right)}=t_0 {t_0}^{\prime} r_1\exp\left(2i\delta_1\right)\)ってこと??
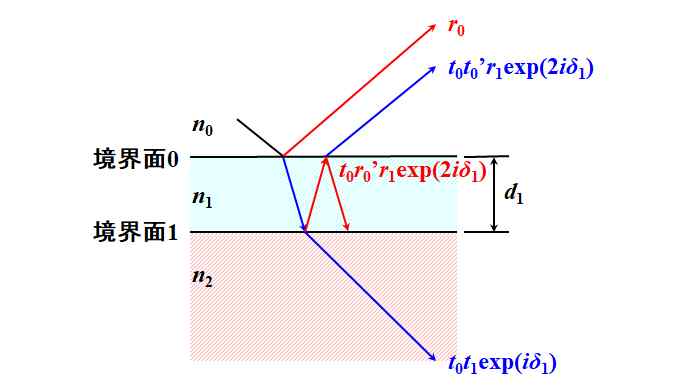 図3.2.6 3回目の反射と透過 |
|
 | そうですね。では、4回目(境界面1)はどうでしょう。 | |
 |
Fresnel反射率は\(r^{\left(4\right)}=t_0 {r_0}^{\prime}{r_1}^2\exp\left(3i\delta_1\right)\)、Fresnel透過率は\(t^{\left(4\right)}=t_0 t_1 {r_0}^{\prime}r_1\exp\left(3i\delta_1\right)\)ですね。
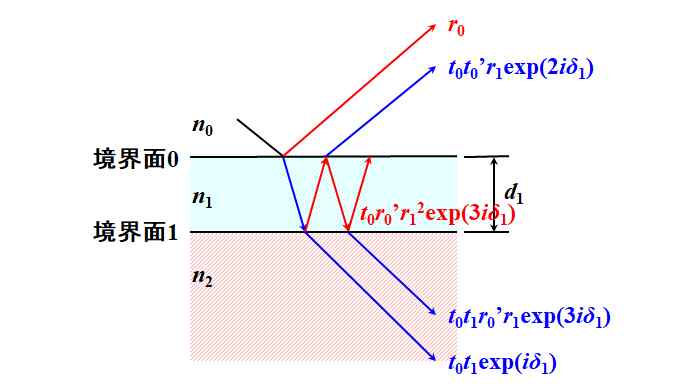 図3.2.7 4回目の反射と透過 |
|
 | もう少し続けましょう。5回目(境界面0)は?? | |
 |
Fresnel反射率は\(r^{\left(5\right)}=t_0 {r_0}^{\prime \thinspace 2}{r_1}^2\exp\left(4i\delta_1\right)\)、Fresnel透過率は\(t^{\left(5\right)}=t_0 {t_0}^{\prime}{r_0}^{\prime}{r_1}^2\exp\left(4i\delta_1\right)\)。
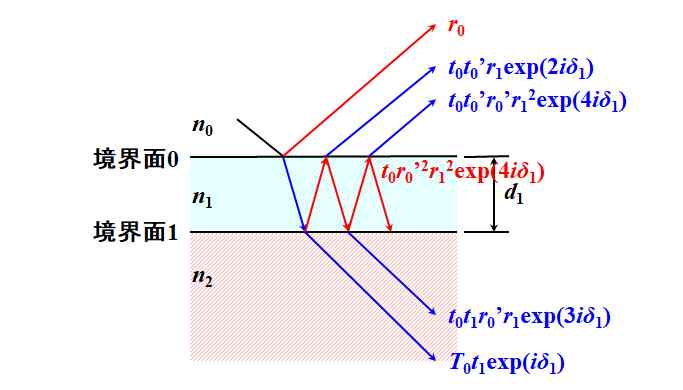 図3.2.8 5回目の反射と透過 |
|
 | 6回目(境界面1)は?? | |
 |
Fresnel反射率は\(r^{\left(6\right)}=t_0 {r_0}^{\prime \thinspace 2}{r_1}^3\exp\left(5i\delta_1\right)\)、Fresnel透過率は\(t^{\left(6\right)}=t_0 t_1 {r_0}^{\prime \thinspace 2}{r_1}^2\exp\left(5i\delta_1\right)\)。
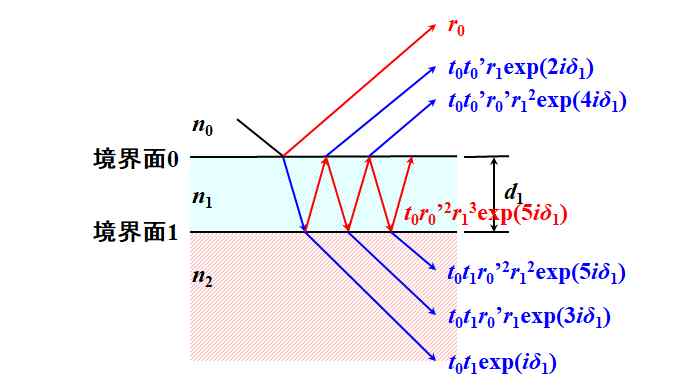 図3.2.9 6回目の反射と透過 |
|
 | 7回目(境界面0)で最後にしましょう。Fresnel透過率だけでいいですよ。 | |
 |
Fresnel透過率は\(t^{\left(7\right)}=t_0 {t_0}^{\prime}{r_0}^{\prime \thinspace 2}{r_1}^3\exp\left(6i\delta_1\right)\)。ふ〜、いい加減、飽きてきた…。
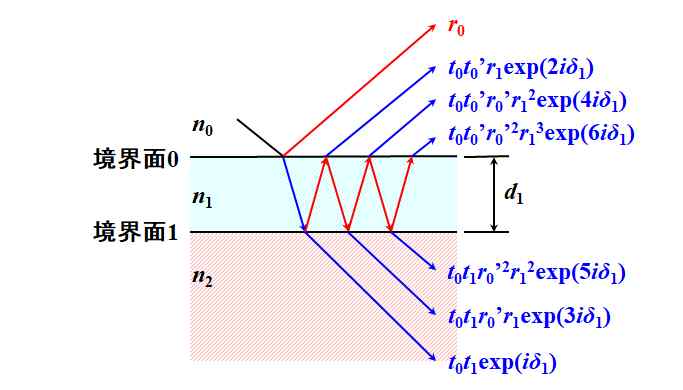 図3.2.10 7回目の透過 |
|
 | 何か法則性が見えてきませんか?? | |
 |
法則ねぇ…。う〜ん。屈折率\(n_0\)の媒質の光は反射光として認識されるけど、並べてみると、 \(r_0\) \(t_0{t_0}^{\prime}{r_0}^{\prime \thinspace 0}{r_1}^1\exp\left(2i\delta_1\right)\) \(t_0{t_0}^{\prime}{r_0}^{\prime \thinspace 1}{r_1}^2\exp\left(4i\delta_1\right)\) \(t_0{t_0}^{\prime}{r_0}^{\prime \thinspace 2}{r_1}^3\exp\left(6i\delta_1\right)\) って書けるから、\(r_0\)だけ除外すると、\(k\)を自然数として\(t_0{t_0}^{\prime}{r_0}^{\prime \left(k-1\right)}{r_1}^k\exp\left(2ki\delta_1\right)\)と整理できそうな気はしますね。 |
|
 | そのトータル振幅反射率を\(\rho_0\)とすれば、 \[ \begin{align*} \rho_0 &= r_0 + t_0 {t_0}^{\prime} \sum_{k=1}^{\infty} {r_0}^{\prime \left( k-1 \right)} \big[ r_1 \exp \left( 2i \delta_1 \right) \big]^k \\ &= r_0 + t_0 {t_0}^{\prime} \sum_{k=1}^{\infty} {r_0}^{\prime \left( k-1 \right)} r_1 \exp \left( 2i \delta_1 \right) \big[ r_1 \exp \left( 2i \delta_1 \right) \big]^{k-1} \\ &= r_0 + t_0 {t_0}^{\prime} r_1 \exp \left( 2i \delta_1 \right) \sum_{k=1}^{\infty} \big[ {r_0}^{\prime} r_1 \exp \left( 2i \delta_1 \right) \big]^{k-1} \\ &= r_0 + t_0 {t_0}^{\prime} \frac{r_1 \exp \left( 2i \delta_1 \right)}{ 1 - {r_0}^{\prime} r_1 \exp \left( 2i \delta_1 \right) } \tag{3.2.1} \end{align*} \] | |
 | 最後は、無限等比級数の和の公式を使いましたね。 | |
 | さて、境界面0の\(t_0\)、\({t_0}^{\prime}\)、\(r_0\)、\({r_0}^{\prime}\)を式2.2.36と式2.2.37を使って書いてみてください。 | |
 | え〜と、 \[ t_0 = \frac{2n_0}{n_0 + n_1} \tag{3.2.2} \] \[ {t_0}^{\prime} = \frac{2n_1}{n_0 + n_1} \tag{3.2.3} \] \[ r_0 = \frac{n_1 - n_0}{n_1 + n_0} \tag{3.2.4} \] \[ {r_0}^{\prime} = \frac{n_0 - n_1}{n_1 + n_0} \tag{3.2.5} \] ですね。 | |
 | つまり、 \[ {r_0}^{\prime} = - r_0 \tag{3.2.6} \] \[ \begin{align*} t_0 {t_0}^{\prime} &= \frac{4 n_0 n_1}{\left( n_0 + n_1 \right)^2} = \frac{\left( n_0 + n_1 \right)^2 - \left( n_0 - n_1 \right)^2}{\left( n_0 + n_1 \right)^2} = 1 - \frac{ \left( n_0 - n_1 \right)^2}{\left( n_0 + n_1 \right)^2} \\ &= 1 - {r_0}^2 \tag{3.2.7} \end{align*} \] が成立します。 | |
 | ということは、式3.2.1は、 \[ \begin{align*} \rho_0 &= r_0 + t_0 {t_0}^{\prime} \frac{r_1 \exp \left( 2i \delta_1 \right)}{ 1 - {r_0}^{\prime} r_1 \exp \left( 2i \delta_1 \right) } = r_0 + \left( 1 - {r_0}^2 \right) \frac{r_1 \exp \left( 2i \delta_1 \right)}{ 1 + r_0 r_1 \exp \left( 2i \delta_1 \right) } \\ &= \frac{ r_0 + {r_0}^2 r_1 \exp \left( 2i \delta_1 \right) + r_1 \exp \left( 2i \delta_1 \right) - {r_0}^2 r_1 \exp \left( 2i \delta_1 \right) }{ 1 + r_0 r_1 \exp \left( 2i \delta_1 \right) } \\ &= \frac{ r_0 + r_1 \exp \left( 2i \delta_1 \right) }{ 1 + r_0 r_1 \exp \left( 2i \delta_1 \right) } \tag{3.2.8} \end{align*} \] ってことかぁ。 | |
 | もう1つの方も片づけましょう。 | |
 |
屈折率\(n_2\)の媒質の光は屈折光として認識されるけど、並べてみると、 \(t_0 t_1{r_0}^{\prime \thinspace 0}{r_1}^0\exp\left(i\delta_1\right)\) \(t_0 t_1{r_0}^{\prime \thinspace 1}{r_1}^1\exp\left(3i\delta_1\right)\) \(t_0 t_1{r_0}^{\prime \thinspace 2}{r_1}^2\exp\left(5i\delta_1\right)\) って書けるから、\(k\)を自然数として\(t_0 t_1{r_0}^{\prime \left(k-1\right)}{r_1}^{\left(k-1\right)}\exp\bigl[\left(2k-1\right)i\delta_1\bigr]\)と整理できそうですね。 |
|
 | そのトータル振幅透過率を\(\tau_0\)とすれば、 \[ \begin{align*} \tau_0 &= t_0 t_1 \sum_{k=1}^{\infty} {r_0}'^{\left( k-1 \right)} {r_1}^{\left( k-1 \right)} \big[ \exp \left( 2i \delta_1 \right) \big]^{k-1} \exp \left( i \delta_1 \right) \\ &= t_0 t_1 \exp \left( i \delta_1 \right) \sum_{k=1}^{\infty} \big[ {r_0}' r_1 \exp \left( 2i \delta_1 \right) \big]^{k-1} \\ &= \frac{ t_0 t_1 \exp \left( i \delta_1 \right) }{ 1 - {r_0}' r_1 \exp \left( 2i \delta_1 \right) } = \frac{ t_0 t_1 \exp \left( i \delta_1 \right) }{ 1 + r_0 r_1 \exp \left( 2i \delta_1 \right) } \tag{3.2.9} \end{align*} \] です。 | |
 | とりあえず、コートしたときの振幅反射率と振幅透過率が求まりましたけど?? | |
 | コーティングの最も実用的な例は、やはり反射防止ですので、その条件を求めてみましょう。 | |
 | よくARコートって言いますけど、それ?? | |
 | そうです。Anti-reflectionの略ですね。 | |
 | ARコートの条件って、要するに\(\rho_0=0\)になればいいんだから、 \[ r_0 + r_1 \exp \left( 2i \delta_1 \right) = 0 \tag{3.2.10} \] では?? | |
 | そうですね。\(\delta_1\)は、 \[ \delta_1 = \frac{2 \pi}{\lambda} n_1 d_1 \tag{3.2.11} \] なので、式3.2.10を満たすように、コートの膜厚と屈折率を選択すれば反射防止機能が達成できます。 | |
 | う〜ん。通常の環境だと、\(n_0\)は空気だから\(1.0\)だし、\(n_2\)はレンズの屈折率だから設計で決まっちゃうし、コート材を選択したら自動的に膜厚が決まっちゃいますね。 | |
 |
なので、単層コートの場合は、あまり融通が利きません。仮に反射率を\(0\)にしたくても、ある特定の波長しか効果がなかったりします。
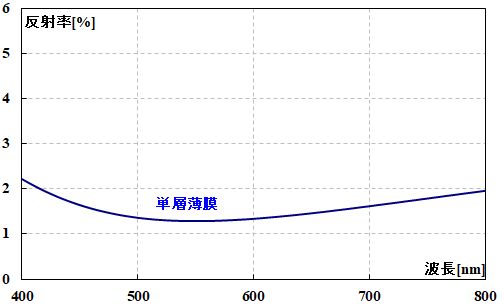 図3.2.11 反射率の波長依存性:単層膜(空気/L/基板) 図3.2.11は、\(n_2=1.516\)とし、\(\lambda\)=550nmで反射率が\(0\)になるように設計した結果ですが、コートに使える材料の制約もあるので、残念ながら\(0\)に抑えることはできませんでした。 |
|
 | だから、多層膜が必要になるわけですね。 | |
 |
LDと組み合わせる光学系なら、基本的にケアすべき波長は1つしかありませんから、単層コートで処理するのは普通のことです。一方で、カメラレンズのような場合になると多層膜は当たり前ですね。実際、2層コートにすると\(\lambda\)=550nmのときに反射率=\(0\)を実現できますし、3層コートにすると反射率=\(0\)となる波長帯域が広がります。
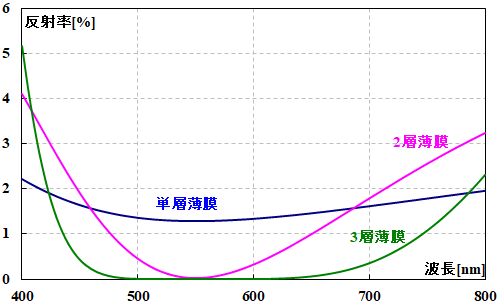 図3.2.12 反射率の波長依存性:2層膜(空気/L M/基板)と3層膜(空気/L 2H M/基板) 10層コートのカメラレンズなんていうのはザラにありますね。 |
|
 | そっか。 | |
 | しかも、ここでの議論は入射角=\(0^{\circ}\)を前提としていたことを忘れてはいけません。 | |
 | あ、忘れてた!!そうすると、もし入射角が変わったら?? | |
 | もちろん、ほしい効果は得られませんよ。多層膜にするのは、入射角依存性を回避する目的もあるんです。 | |
 | 教授。図3.2.11とか図3.2.12のタイトルにあるHとかLって?? | |
 | これは、使用しているコート材の屈折率のことを意味します。Hは相対的に屈折率の高い材料、Lは相対的に屈折率の低い材料です。Mは中間ってことですね。 | |
 | それだと、材料が特定できないですよね。 | |
 | 確かにそうですが、材料のバリエーションはそんなにたくさんあるわけではないですし、HならTiO2やMgF2、LならSiO2やZnO2、MならAl2O3という具合に、非常によく使われる材料というのも決まってますからね。だから慣例的に、そういう記載をするのです。 | |
 | 数字は?? | |
 | 単独でLとか書かれている場合は、通常は\(d_1=\cfrac{\lambda}{4n_1}\)というお約束になっています。\(d_1\)は物理膜厚ですが、これに屈折率\(n_1\)を掛けた膜厚は光学膜厚とも呼ばれます。 | |
 | つまり、光学膜厚が\(\cfrac{\lambda}{4}\)というのがお約束ってことですね。あ、そうか。そのときは\(\delta_1=\cfrac{\pi}{2}\)で、式3.2.10の\(\exp\left(2i\delta_1\right)\)が実数(\(-1\))になるからですね。 | |
 | そういうことです。ですから、"空気/L 2H M/基板"と書かれていたら、相対的に高い屈折率のコート材で光学膜厚\(\cfrac{\lambda}{2}\)のコーティングを2層目に実行する、という意味になるのです。 |
| 前頁へ | 戻る | 次頁へ |