 |
多層膜にしていくと、反射防止が可能な波長帯域が広がっていくことを見てきましたが、特に繰り返し構造を持つコーティングのことを1次元フォトニック結晶と呼ぶことがあります。
 図3.2.13 1次元フォトニック結晶 |
|
 | コート材って基本的に誘電体なんじゃないですか??結晶?? | |
 | 慣例的にそう呼ぶんですよ。一般的には誘電体多層膜の方が通りがいいかもしれませんね。 | |
 | 私も、そっちの方を使います。 | |
 | 要するにフォトニック結晶という考え方があって、その括りで見ると誘電体多層膜は1次元フォトニック結晶だってことです。また、その考え方に従うと、反射率が\(0\)になる波長帯域のことをフォトニック・バンドギャップと言います。 | |
 | お、その言い方、恰好いいですね。 | |
 | このような周期構造を持つ構造体(1次元フォトニック結晶)が、ある周波数の光を結晶内から排除する機能を持つと指摘した(論文)のはRayleighです。その後、これを拡張した2次元、3次元のフォトニック結晶も研究されましたが、つい最近までは絵に描いた餅という捉え方しかされていませんでした。 | |
 | 作れないから?? | |
 |
そうです。特に、3次元フォトニック結晶はYablonovitchによって、入射角依存性も偏光依存性もない反射防止を実現できることが理論的に示されて(論文)いて、この結晶の実現に向けていろいろ研究されていますが、残念ながら実用化に至っていないのが現状ですね。ちなみに、このような性質はフル・バンドギャップと言います。
 Eli Yablonovitch(1946~) |
|
 | 2次元、3次元のフォトニック結晶ってどういう構造ですか?? | |
 |
こういう構造体ですね。
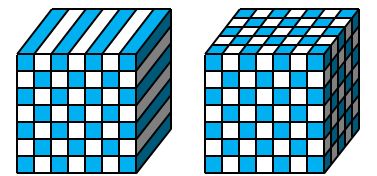 図3.2.14 左:2次元フォトニック結晶 右:3次元フォトニック結晶 |
|
 | お~、3次元フォトニック結晶ってルービック・キューブみたい。でも、2次元フォトニック結晶は、入射光からするとストライプ構造に見えるから、偏光依存性が強そうですね。 | |
 | そうですね。偏光方向がストライプに平行か垂直かで、発現される機能が大きく異なってきます。こういう性質を上手く利用して、光を排除したり、或いは逆に閉じ込めたりするんです。 | |
 | 光ファイバーも光の閉じ込め効果を利用したものですよね。 | |
 | その観点では光ファイバーとフォトニック結晶は相性がいいですからね、2つを組み合わせて反射の損失を低減する研究もやられてますよ。後は、2次元フォトニック結晶を使った偏光制御もありますね。 | |
 | う~ん。でも、そういう機能って、フォトニック結晶じゃなくても実現できますよね?? | |
 | 従来の技術を、すべてフォトニック結晶で置き換えるのは現実的ではないです。よっぽど製造がしやすく、コストが安いなら話は別ですが、そういうわけでもないですしね。だから、適材適所で実用化していくことになるでしょう。 | |
 | 狭い領域だったらハマりそうな気はしますね。 | |
 | それと、フォトニック結晶は理論的に議論するのが難しい。 | |
 | え、そうなんですか?? | |
 | 1次元フォトニック結晶でも容易ではないです。例えば、式1.2.3に式1.2.2を代入すると、 \[ \nabla^2 u = - \frac{\omega^2}{{v_p}^2}u \tag{3.2.12} \] と書けますが、屈折率\(n\)を伝搬する光速は式1.8.3より\(v_p=\cfrac{c}{n}\)ですから、 \[ \nabla^2 u = - \frac{n^2 \omega^2}{c^2}u \approx - \varepsilon_r \frac{\omega^2}{{c}^2}u \tag{3.2.13} \] です。 | |
 | さりげなく式1.8.5を使いましたね。 | |
 |
ここで、
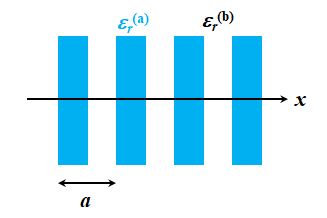 図3.2.15 1次元フォトニック結晶の例 比誘電率\(\varepsilon_r\)が図3.2.15のような繰り返し構造をしているとすれば、 \[ \varepsilon_r \left( x + a \right) = \varepsilon_r \left( x \right) \tag{3.2.14} \] と書けますが、残念ながらこうなった時点でこれ以上、解析的に解くことはできません。 |
|
 | え~、そうなんだ。 | |
 |
2次元や3次元に拡張した繰り返し構造は並進対称性と呼ばれますが、このときに電磁波が満たすべき条件の1つとしてBlochの定理というのがあります(論文)。
 Felix Bloch(1905~1983) その定理を使うと、電磁波の形を決めることはできますが、フォトニック・バンドギャップがどういう条件で出現するかといったようなことは、基本的にFDTD(時間領域差分法)などの手法を使ってコンピューターによる数値計算をするしかありません。 |
|
 | そうすると、フォトニック結晶の性質とかを理論体系的に調べるのは難しそうですね。 | |
 | ですから、大胆な近似を行ったりして大枠の姿を捉えたうえで、細かい検討は数値計算に頼るという感じになるんですよ。 |
~サブ波長構造体~
 |
さて、反射防止を実現できるもう1つの技術としてSWS(サブ波長構造体)を紹介します。
 図3.2.16 SWS(1) |
|
 | あれ??それって前にやりましたね。 | |
 | 波長より小さな微細構造であれば、光はそれを構造体と認識することができない、という性質を上手く利用した技術ですね。 | |
 | 構造物の屈折率\(n_{\rm str}\)と空気の屈折率の中間くらいの屈折率を持つ薄膜を通過しているように感じる気がしますね。 | |
 | そうです。実際は、Lorentz-Lorenzの式で、\(\cfrac{n_2-1}{n_2+2}\)が密度の関数でしたから、光の感じる実効的な屈折率を\(n_{\rm eff}\)、構造体の空間占有率を\(d_a\)とすると、 \[ \frac{{n_{\rm eff}}^2-1}{{n_{\rm eff}}^2+2} = d_a \frac{{n_{\rm str}}^2-1}{{n_{\rm str}}^2+2} \tag{3.2.15} \] を解いて\(n_{\rm eff}\)を求めることになります。 | |
 | 構造体の形状は図3.2.16じゃないとダメですか?? | |
 |
いえ。「錐」のような構造でも、同じような効果を得ることができます。
 図3.2.17 SWS(2) |
|
 | これだと、頂点から基板に向かって屈折率が連続的に変化するようなイメージかな?? | |
 |
そうですね。
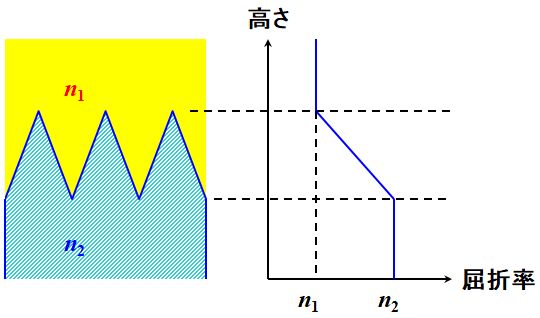 図3.2.18 SWSで光の感じる屈折率の変化 図3.2.18のような具合に屈折率が変化する多層膜を通過しているように光は感じるでしょう。 |
|
 |
その場合は(図3.2.19)、横方向に薄くスライスして(a)、サッカラの階段ピラミッドみたいにして(b)、それぞれの層の平均屈折率を求めて(c)議論するわけですね??
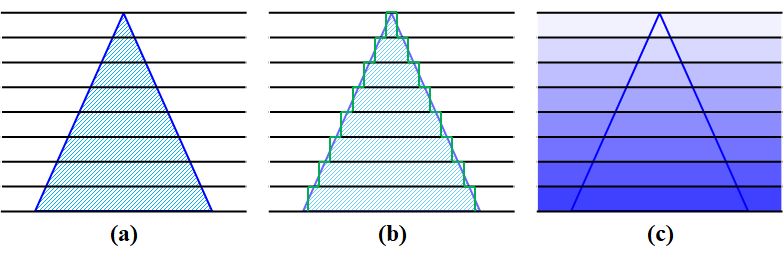 図3.2.19 SWSを等価薄膜へ置換する方法 |
|
 | それでOKです。 | |
 | でも―。こんな構造物をガラス・レンズに作れますかね?? | |
 | ガラス・レンズに直接は無理です。しかし、モールド成型で加工できるレンズの反射防止には効果的だと考えられます。 | |
 | ガラス・モールドとか樹脂とかですか?? | |
 | そうです。そもそも樹脂の場合、適応できるコート材も少ないですしね。 | |
 | そうなんですか?? | |
 | コーティングは、高温・高圧でコート材を蒸気にしてレンズ面に積層して形成するんですが、樹脂レンズをそのチャンバーの中に入れるわけにはいきません。ですから、樹脂レンズをコーティングする場合、低温蒸着が必要になります。でも、低温蒸着材料は極端に少ないんですよ。 | |
 | そういうことか…。ムムム。ひょっとして環境変動があると、樹脂の方が線膨張係数が大きいから、コートがダメになるのでは?? | |
 | ひび割れですね。確かに、それは大問題です。その点、SWSであれば、金型の方に構造物を加工し、成型の過程でそれを転写するだけだから、樹脂レンズに対してSWSはかなり期待の大きい技術と言うことができます。 | |
 | でも、加工上の限界もありますよね。だって、大口径のレンズに微細加工を施すなんて、あまり現実的とは思えないですけど。 | |
 | それと、曲率半径のきつい曲面にSWSを加工するのも難しいですね。金型からレンズが抜けるように設計する必要があるので、その制約が大きいです。 | |
 | そうすると、スマホ用のカメラ・レンズくらいしか応用できそうにないですね。 | |
 | 確かに、商業的にSWSを実用化した例はあまり耳にしませんね。以前、テラヘルツ波の波長選択フィルターとしてSWSを使ったことがありますが、ひょっとすると長波長の電磁波の領域では、いろいろな応用が検討されているかもしれません。 | |
 | ほしい機能が低コストで手に入るなら、わざわざSWSに手を出す必要もないか…。 | |
 | ただ、非常に似たようなSWC(Sub wavelength coating)という技術を㈱キヤノンが開発して、実用化したことがありますね。 | |
 | お、㈱キヤノン!!やりますね。 | |
 |
EF24mm F1.4L II USM というカメラに初めて商品搭載されました。
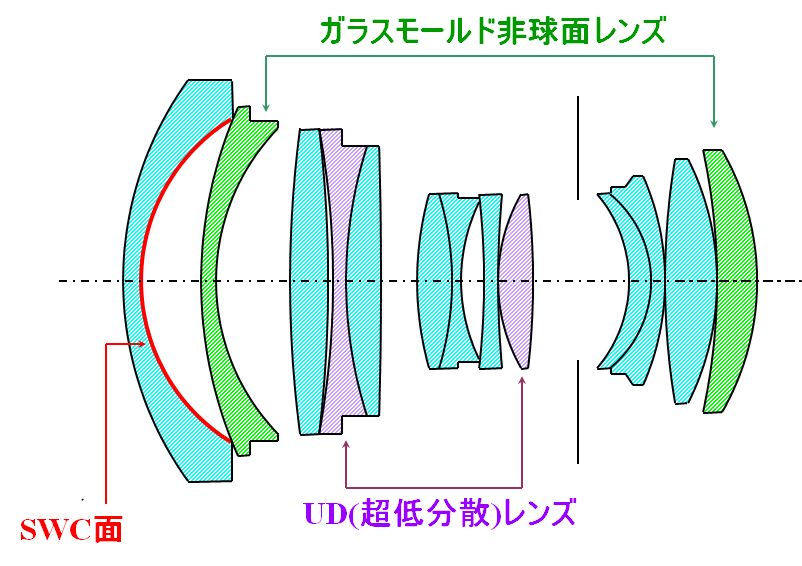 図3.2.20 EF24mm F1.4L II US |
|
 | SWSと何が違うんですか?? | |
 | SWCはコーティングと言うくらいですからね。コートの一種なんです。レンズ面にアルミニウム・アルコキシド、安定化剤、触媒などを混合したコーティング液をスピン・コート法で塗布して焼結すると、表面にアモルファス・アルミナ膜ができます。これを温水に浸漬させることで凹凸構造を持った微結晶膜を形成する(論文)のです。 | |
 | ずいぶん簡単そうですね。 | |
 | SWSは金型に微細構造を掘り込むので、どちらかというと引き算のイメージですが、SWCはコーティングなので足し算のイメージですね。発想がまるで逆です。 | |
 | お~。確かに。でも―。綺麗な"とんがりコーン"に制御できますかね?? | |
 |
できないでしょう。しかし、屈折率の平均値が重要だとすれば、1つ1つの構造体が粒揃いでなくても、求める機能は得られると考えられますね。
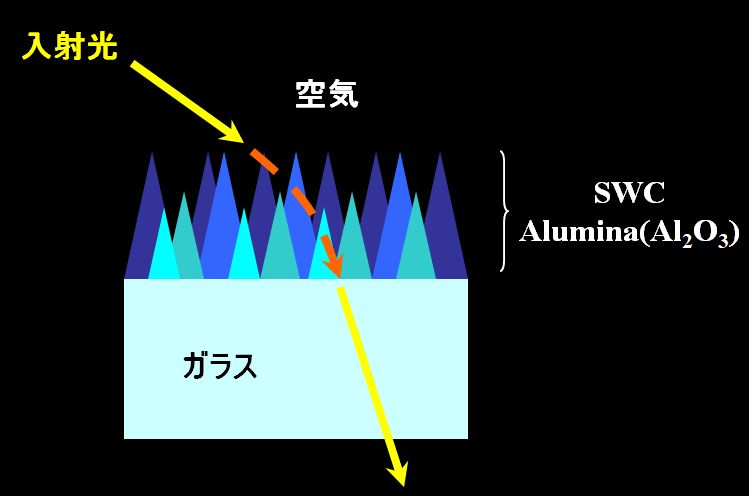 図3.2.21 SWC |
|
 | そしたら、すべてのレンズ面をSWCで処理すればいいですね。 | |
 | いえ。それはそれで難しいと思います。 | |
 | え~、何でですか?? | |
 | Al2O3の屈折率が\(1.77\)くらいなので、基板となるレンズの屈折率との相性を考えないと、反射防止の効果が充分に発揮されないからです。 | |
 | ん??そうすると、図3.2.20の左側のレンズの屈折率っていくですか?? | |
 | \(1.84\)程度ですね。 | |
 | 相性は?? | |
 | よくないはずです。 | |
 | じゃぁ、ダメじゃないですか。 | |
 | ですから、レンズ基板とSWCの間にバッファーとなる薄膜を作って、その問題を回避しているんです。 | |
 | あらら。そうすると、工程が1つ増えますね。 | |
 | だから、すべてのレンズ面にSWCというわけにもいかないのだと予想されます。 | |
 | アルミナ以外で、こういう技が使えればいいんですけどね。 | |
 | 同じような化学的性質を持って、都合のいい屈折率を持つSWC用の材料は、そう簡単に手に入らないでしょう。 | |
 | やっぱり適材適所ってことか…。 |
| 前頁へ | 戻る | 次頁へ |