 | さて、PBSについて触れておきましょう。 | |
 | これも、薄膜設計なんですか?? | |
 |
そうです。PBSは、入射した光のうち、\(s\)偏光成分を反射させ、\(p\)偏光成分を透過させる機能を持った光学素子です。
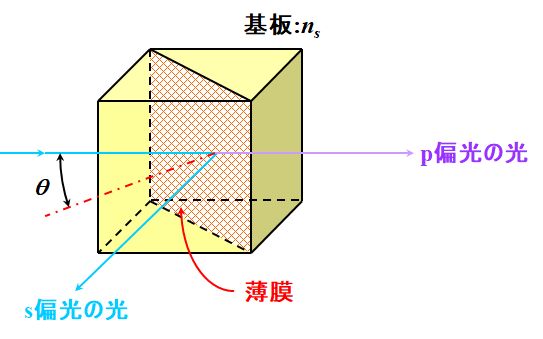 図3.2.22 PBS |
|
 | 偏光の違いを利用して光を分割するわけですね。 | |
 | だから、Snellの法則とBrewster条件を考慮して薄膜の材料を選んでやれば設計できそうだな、ということも分かると思います。 | |
 | \(p\)偏光の反射成分だけ\(0\)になるっていうやつか…。 | |
 |
例えば、薄膜を挟んでいる基板の屈折率を\(n_s\)とし、2層の薄膜で光を分割することを考えてみましょう。
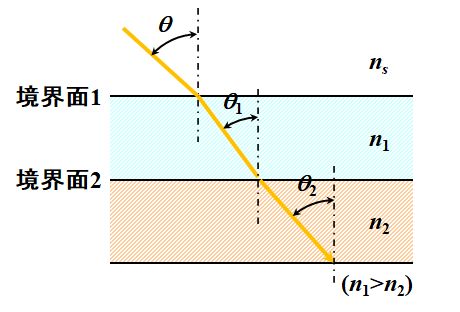 図3.2.23 PBSの薄膜理論 このとき、境界面1でSnellの法則が成立します。 |
|
 | つまり、 \[ n_s \sin \theta = n_1 \sin \theta_1 \tag{3.2.16} \] ですね。 | |
 | 次に、境界面2で光を分割するとすれば、そこでBrewster条件が満たされないといけません。 | |
 | ということは、 \[ \tan \theta_1 = \frac{n_2}{n_1} \tag{3.2.17} \] ってことか。 | |
 | 三角関数は、 \[ \sin^2 \theta_1 + \cos^2 \theta_1 = 1 \tag{3.2.18} \] が常に成立しますから、式3.2.18に式3.2.17を代入してください。 | |
 | ムムム。式3.2.17をちょっと変形しないといけないですね。 \[ \frac{\sin \theta_1}{\cos \theta_1} = \frac{n_2}{n_1} \quad \Leftrightarrow \quad \cos \theta_1 = \frac{n_1}{n_2} \sin \theta_1 \] だから、 \[ \begin{align*} &\sin^2 \theta_1 + \left( \frac{n_1}{n_2} \right)^2 \sin^2 \theta_1 = \frac{{n_1}^2 + {n_2}^2 }{{n_2}^2} \sin^2 \theta_1 = 1 \\ &\Leftrightarrow \quad \sin^2 \theta_1 = \frac{{n_2}^2}{{n_1}^2 + {n_2}^2} \tag{3.2.19} \end{align*} \] ですね。 | |
 | で、最後に式3.2.16を代入です。 | |
 | ん~と、 \[ \left( \frac{n_s}{n_1} \sin \theta \right)^2 = \frac{{n_2}^2}{{n_1}^2 + {n_2}^2} \quad \Leftrightarrow \quad {n_s}^2 = \frac{{n_1}^2 {n_2}^2}{\sin^2 \theta \left( {n_1}^2 + {n_2}^2 \right) } \tag{3.2.20} \] かな。 | |
 | これが、PBSの成立条件になります。通常は\(\theta=45^{\circ}\)で設計することが多いでしょうから、 \[ {n_s}^2 = \frac{2 {n_1}^2 {n_2}^2}{{n_1}^2 + {n_2}^2 } \tag{3.2.21} \] ですね。 | |
 | 式3.2.21を満たすようなコート材を選ぶってことか。 | |
 |
あくまで2層で設計した場合の話ですがね。実際は、もっと多層膜にして性能の向上を目指します。
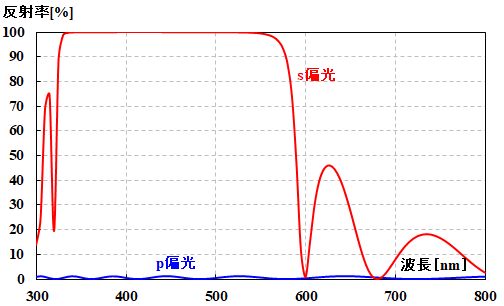 図3.2.24 分離の波長依存性:基板/(L/2 H L/2)7/基板 |
|
 | 図3.2.24は21層ってことですね。かなりいい具合に分離できてるな~。 |
~光の合成~
 | 当然、光を逆に入射させると、それぞれの光を合成することも可能です。 | |
 | お、確かに。 | |
 |
今でこそ、マルチビームのLDやVCSELは珍しくない光源素子になりましたが、かつてはシングルビームのLDを2個使い、それを合成することでMFPの高速・高密度を実現していました。
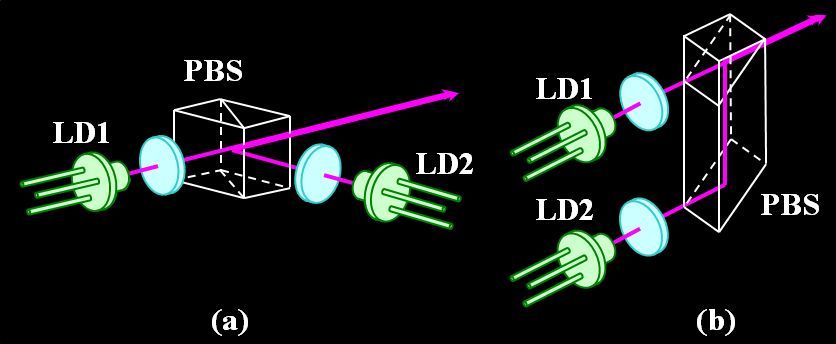 図3.2.25 2つのLDの合成方式 |
|
 | 横に並べて合成する方法(a)と、縦に並べて合成する方法(b)かぁ。 | |
 |
(a)は、1990年に㈱日立製作所が発売したH-6286に実装されたタイプ(論文)ですね。
 図3.2.26 H-6286 こんな光学系です。 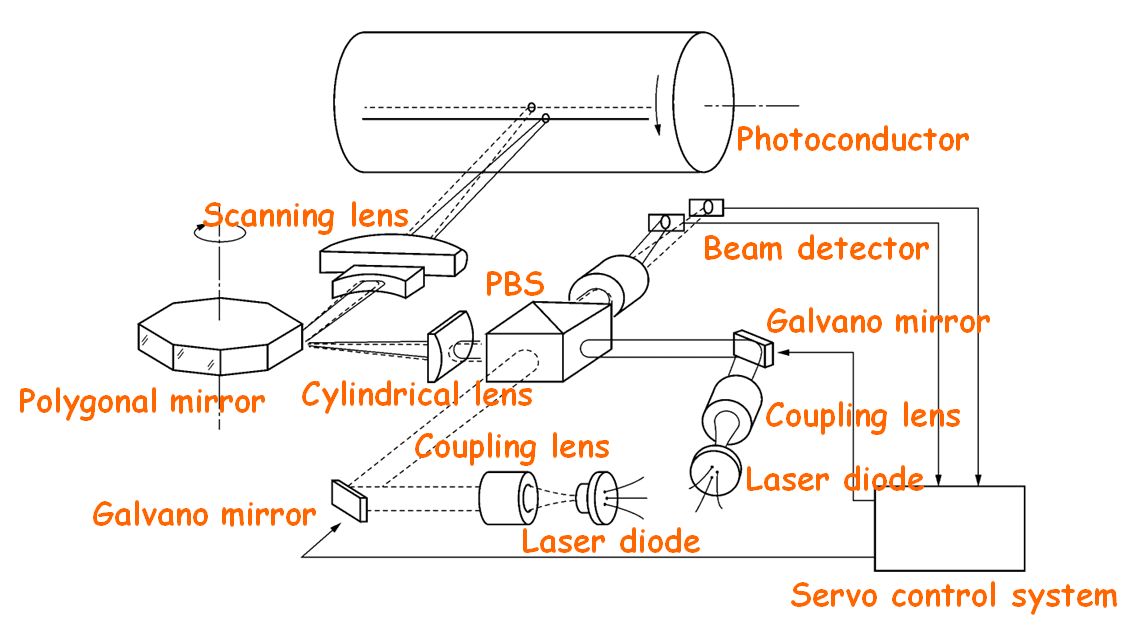 図3.2.27 H-6286の光学系 |
|
 | 何だか、凄く大がかりな光学系ですね。ガルバノ・ミラーとかが実装されてますけど。 | |
 | 感光体上の走査線ピッチは、LD1とLD2の位置関係で決まるので、それが適正かどうかを検知して、ズレてたら補正しないといけません。ガルバノ・ミラーはそのための仕掛けですね。 | |
 | てことは、(b)も同じ?? | |
 |
(b)は、1998年に㈱リコーが発売したimagio MF6550に実装されたタイプになります。
 図3.2.28 imagio MF6550 このタイプは、LDからPBSまでを1つのユニットに作り込んでいるので、光学系は単純です。 |
|
 | でも、走査線ピッチがいつも安定しているとは限らないですよね。 | |
 | ですから、感光体の端っこで走査線ピッチを検出したら、その情報をフィードバックして、このユニットを、ビームの進む向きを軸に回転させるんですよ。 | |
 | なるほど~。教授。(a)にしろ(b)にしろ、PBSで一方のビームは反射させないといけないから、そのLDは\(90^{\circ}\)回転させないといけませんよね。 | |
 | そうしたいのは山々なんですが―。LDから放射されるビームの広がりパターンは楕円形状になることを覚えてますか?? | |
 | はい。 | |
 | 2つのビームは感光体に到達したときに同じスポット形状にならないといけません。しかし、片方のLDを\(90^{\circ}\)回転してしまうと、縦長と横長の楕円ビームが混在することになり、それぞれを両立させるレンズ設計が難しくなるのです。 | |
 | う~ん。LDを\(90^{\circ}\)回転させずに、偏光の方向だけ\(90^{\circ}\)回転させたいのか…。あ!!だったら、1/2波長板を使えばいいのでは?? | |
 | そうですね。(b)のケースだと、LD2の光路のPBS入射面に1/2波長板を挿入すると、その問題は解決しそうです。しかし、そうすると別の問題が発生します。 | |
 | 一難去ってまた一難だ。 | |
 | 光学素子に入射する光の偏光方向によりシェーディングが変わってしまう話は覚えていますか?? | |
 | そうか。LD1とLD2の偏光方向が直交しているから、感光体に到達したときの光量変動が揃わなくなっちゃうんですね。 | |
 | そのため、光量ムラが非常に目立ちやすくなります。 | |
 | でも、LD2の偏光方向を元に戻そうと思っても、LD1から放射されたビームと光路が重なっているから、どうしようもないですね。 | |
 | そうでもないですよ。例えば、PBSの出射側に1/4波長板を挿入したらどうでしょう?? | |
 | お??お??そうか!!どっちも円偏光に変換されるから、シェーディングが揃いそうですね。 | |
 |
つまり、最終的には図3.2.29のような形体になるわけです。
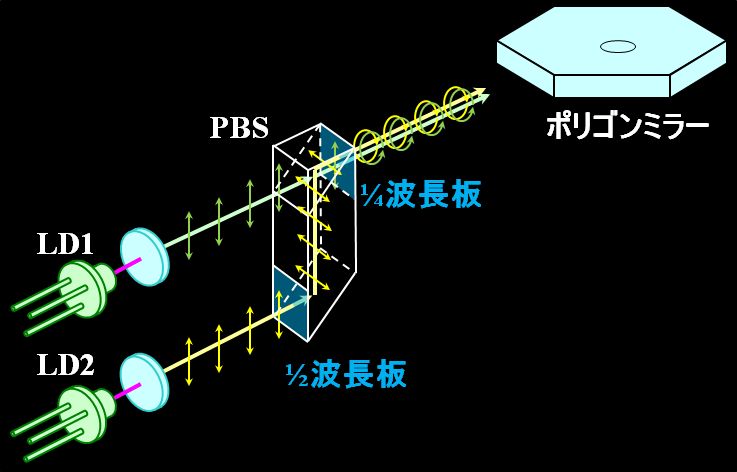 図3.2.29 合成方式の最終形体 |
|
 | でもなぁ。いろいろな素子が組み合わさっているから、何か高そうですね。 | |
 | そうですね。それに位置調整が大変です。だから、マルチビームのLDが急速にプライス・ダウンするに伴って、こういうゴテゴテした方式は駆逐されていったのです。 |
~光アイソレーター~
 | PBSを上手く利用した例としてもう1つ、光アイソレーターを見ておきましょう。 | |
 | アイソレート(isolate)って、要するに分離するってこと?? | |
 |
そうです。例えば、ハイパワーのLDを使って金属などを加工することを想定します。
 図3.2.30 レーザ加工 このとき、照射エネルギーのすべてが加工に使われるわけではありません。当然、金属は反射率が高いですから、一部は反射して、入射ビームと同じ光路で光源側に戻っていきます。  図3.2.31 レーザ加工で反射したビーム |
|
 | ん~。何か起こりそうですね。 | |
 | 例えば?? | |
 | そうだなぁ。放射しているビームと、戻ってきたビームが干渉しそうですね。 | |
 | はい。そうなると、放射ビームの光量が不安定になってしまいます。 | |
 | ちゃんと加工できなくなっちゃいますね。 | |
 | そこで、戻ってくるビームを別の光路に導いてやる必要があるわけです。 | |
 | それが、光アイソレーターってことですね。 | |
 | いろいろな方式があるんですが、ここではPBSを使ったオーソドックスな方法を紹介します。 | |
 | あ~、何か読めてきましたよ。つまり、入射ビームの偏光に対して、戻ってきたビームの偏光を\(90^{\circ}\)回転させればPBSで分離できそうですもんね。 | |
 | 着眼点はよいです。 | |
 | 行って帰ってで偏光を\(90^{\circ}\)回転させればいいんだから、1/4波長板があれば解決するのでは?? | |
 | 大正解です。 | |
 | やったね。 | |
 |
光路にPBS+1/4波長板を設置すれば、入射した直線偏光のビームはPBSを透過後、1/4波長板により円偏光に変換されます。
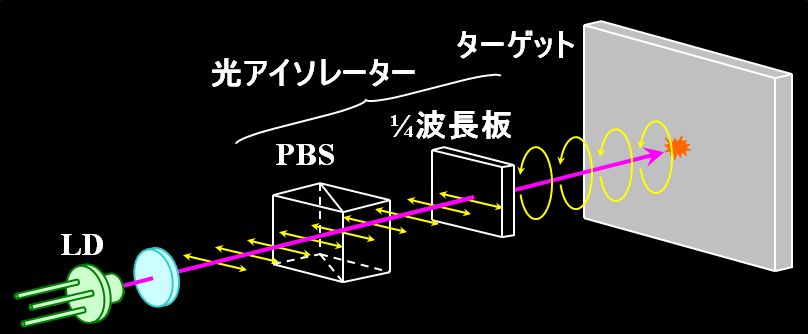 図3.2.32 光アイソレーターの機能(1) ところが、そのビームが反射して戻ってくると、同じ円偏光なんですが、ビームからすると逆回転しているように見えるわけです。 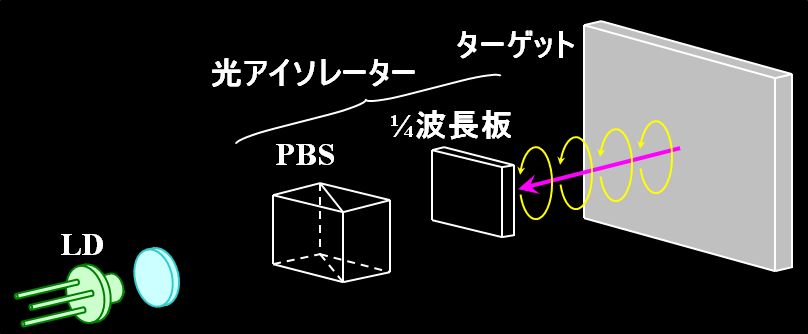 図3.2.33 光アイソレーターの機能(2) そのため、1/4波長板を透過するときには、\(90^{\circ}\)回転した直線偏光となり、PBSの作用で別の光路に導かれるのです。 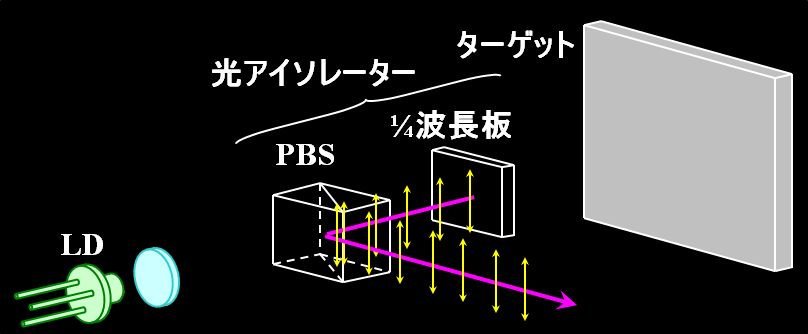 図3.2.34 光アイソレーターの機能(3) |
|
 | 何か、パズルみたいですね。 |
| 前頁へ | 戻る | 次頁へ |