 | 薄膜理論で多重干渉を扱いましたが、多重干渉で1つエピソードを思い出したので、それを紹介しましょう。 | |
 | 思い出話…。 | |
 |
あるLSUを開発していたときのことです。LDの注入電流¥(I_{¥rm op}¥)と感光体上の光量¥(P¥)の関係を評価していたところ、図3.2.35のような奇妙な結果が得られました。
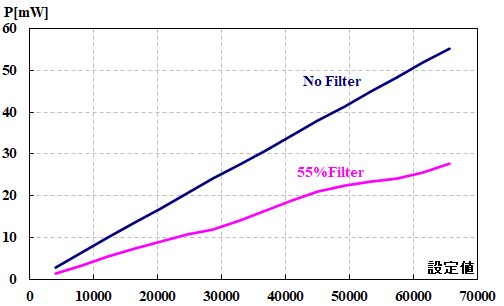 図3.2.35 ¥(I_{¥rm op}¥)と¥(P¥)の関係(1) |
|
 | 何か、フィルターがある方は波打ってますね。 | |
 |
傾き成分を除去すると、うねっているのがはっきりします。
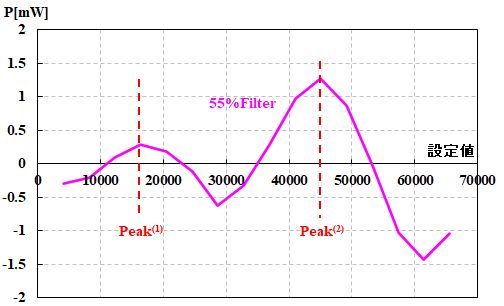 図3.2.36 ¥(I_{¥rm op}¥)と¥(P¥)の関係(2) |
|
 | 設定値というのは?? | |
 | 電流はPCで設定するデジタル値で制御していたので、その数値ですね。¥(I_{¥rm op}¥)に相当するものだと思ってもらえればよいです。このようなうねりが、LSUに搭載されているNDフィルターの影響によるものであることは、それを除去した状態での測定結果が¥(P¥propto I_{¥rm op}¥)になったことから、すぐに判明しました。 | |
 | NDフィルター?? | |
 | 余分な光量をカットするための光学素子です。Neutral Densityの略称ですね。 | |
 | それが多重干渉を発生させたということですね?? | |
 |
尤も、それは当初、1つの仮説でしかありませんでした。図3.2.2で、¥(n_2=n_0¥)とすれば、空気中に置かれた平行平板ガラスを意味することになりますね??
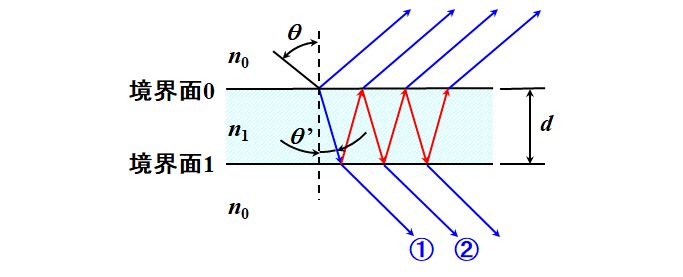 図3.2.37 エタロン効果 |
|
 | 確かに。 | |
 | 当然、この場合も多重干渉は起きますが、この現象をエタロン効果と呼ぶことがあります。 | |
 | 多重干渉ってことは、やっぱり無限等比級数の和?? | |
 | 厳密にはそうですが、NDフィルタなので、何度も反射する成分は急速にエネルギーが減少していきます。よって、正規の透過光①と、境界面0と境界面1を1回ずつ反射して出てきた光②の干渉だけを考えれば充分でしょう。 | |
 | その位相差¥(¥Delta¥phi¥)が問題ってことですね。そうすると(¥(n_1=n¥))、 ¥[ ¥begin{align*} ¥Delta ¥phi &= ¥frac{2 ¥pi}{¥lambda} n ¥times 2 d ¥cos ¥theta^{¥thinspace ¥prime} = ¥frac{2 ¥pi}{¥lambda} ¥times 2 d ¥sqrt{ n^2 - ¥left( n ¥sin ¥theta^{¥thinspace ¥prime} ¥right)^2 } ¥¥ &= ¥frac{2 ¥pi}{¥lambda} ¥times 2 d ¥sqrt{ n^2 - ¥sin^2 ¥theta } ¥tag{3.2.22} ¥end{align*} ¥] かな。 | |
 | 途中で、Snellの法則を適用したわけですね。 | |
 | だけど、注入電流¥(I_{¥rm op}¥)を変化させても、¥(d¥)とか¥(¥theta¥)とか¥(n¥)が変化するとは思えないですけど。 | |
 | そうすると、必然的に¥(¥lambda¥)が変化すると考えるべきですね。 | |
 | 波長、変わりますか?? | |
 |
それを調べたのが、図3.2.38です。
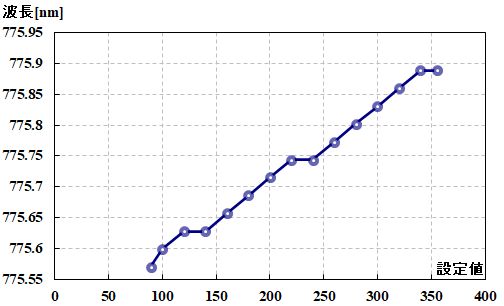 図3.2.38 ¥(I_{¥rm op}¥)と¥(¥lambda¥)の関係 |
|
 | へぇ。意外と変わるもんですね。でも、階段状に変化するのか。 | |
 | LDの特徴ですね。そうすると、図3.2.36のPeak(1)とPeak(2)に対応する波長が割り出せます。よって、 ¥[ ¥left¥{ ¥ ¥begin{array}{l} ¥cfrac{2 ¥pi}{¥lambda^{¥left( 1 ¥right)}} ¥times 2 d ¥sqrt{ n^2 - ¥sin^2 ¥theta } = 2 m ¥pi ¥¥ ¥cfrac{2 ¥pi}{¥lambda^{¥left( 2 ¥right)}} ¥times 2 d ¥sqrt{ n^2 - ¥sin^2 ¥theta } = 2 ¥left( m + 1 ¥right) ¥pi ¥end{array} ¥right. ¥] の連立方程式を解けばよい、というふうに問題を立て直すことができるのです。 | |
 | 下の式から上の式を引けば、 ¥[ ¥left( ¥cfrac{1}{¥lambda^{¥left( 2 ¥right)}} - ¥cfrac{1}{¥lambda^{¥left( 1 ¥right)}} ¥right) ¥times 2 d ¥sqrt{ n^2 - ¥sin^2 ¥theta } = 1 ¥tag{3.2.23} ¥] だから、実測値を代入して式3.2.23が成立すればいいわけですね。 | |
 | 実際は、¥(d¥)を求めて、その値が図面と一致したことで、多重干渉の仮説が証明されました。 |
〜金属ミラー〜
 | ついでに、金属ミラーについてだけ、少し見ておきましょう。 | |
 | 金属ミラーって、普通はガラスに金属膜を蒸着したものですよね。 | |
 |
一般的にはアルミニウム(Al)が使われると思います。他にも金(Au)、銀(Ag)、銅(Cu)などが代表的な材料と言えるでしょう。
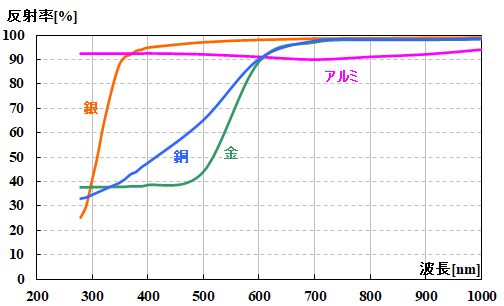 図3.2.39 金属ミラーの反射率の波長依存性 |
|
 | AuとCuは赤外域で反射率が大きいですね。 | |
 | ですから、赤外用ミラーで使われることが多いですね。 | |
 | 反射率の高い波長帯域が広いのはAgか。 | |
 | しかし、Agは空気中でAg2Sを形成して黒く変色してしまうのが欠点です。お風呂場の鏡が黒くなるのは、このせいですね。 | |
 | あれってカビじゃないんですか?? | |
 | 違います。保護塗料が経年劣化で剥がれ、そこから皮膚や髪の毛のタンパク質に含まれている硫黄が入って錆びていくんですよ。 | |
 | Alは、そんなに反射率が高くないけど、赤外領域から紫外領域までそこそこの反射率をキープしているから、一番オールマイティーな気がしますね。 | |
 | また、空気中で自然酸化膜を形成して、これが保護膜として機能するので、耐久性が高いというメリットもあります。尤も、工業的には、不安定な自然酸化膜ではなく、SiO2などの酸化物誘電体層を保護膜として蒸着します。 | |
 | LSUだと、折返しミラー、ポリゴン・ミラーってところですか?? | |
 | そうですね。ポリゴン・ミラーはAlの切削加工で作製され、保護膜としてSiO、或いはSiO2を蒸着するのが一般的でしょう。 | |
 | そっか。Alを蒸着じゃなくて、Alそのものの加工品なわけですね。 | |
 | かつて、㈱キヤノンでCuを蒸着したポリゴン・ミラーが搭載されたこともありました。 | |
 | その狙いは?? | |
 | LDの波長が780nmであることを考えると、反射率の向上でしょうね。 | |
 | 折返しミラーは、やっぱり反射率を上げたいから、コーティングしますよね。 | |
 | そうですね。たいていは、Alの上にMgF2、TiO2、SiO2、H4などで誘電体多層膜を形成するのが一般的です。 | |
 | H4?? | |
 |
メルク・アンド・カンパニーが開発した、TiとLaを混合して得られる高屈折材料です。LSUで使われる反射光学素子としては、他にも¥(f¥theta¥)ミラー(論文)がありますね。
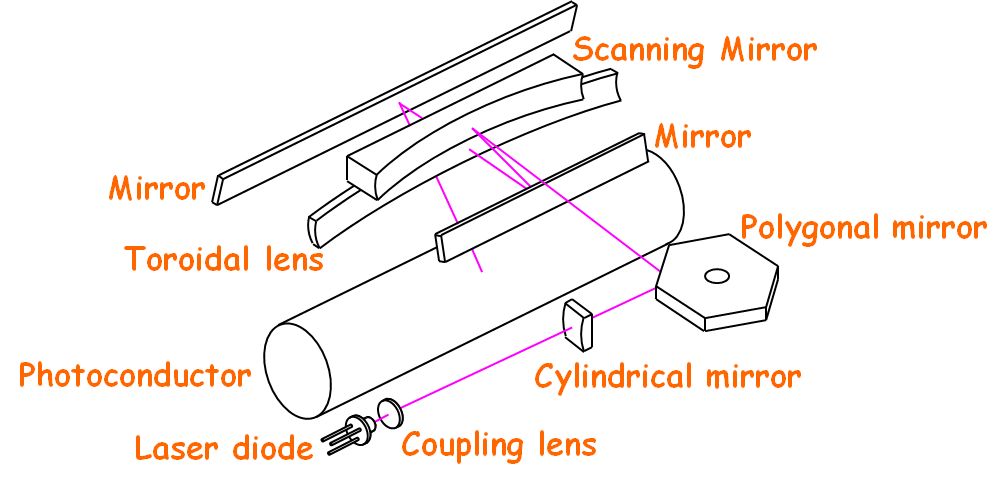 図3.2.40 ¥(f¥theta¥)ミラー走査光学系 |
|
 | それは、¥(f¥theta¥)レンズの代わり?? | |
 | そうです。 | |
 | わざわざ¥(f¥theta¥)ミラーを使う狙いは?? | |
 | 入射するビームの波長変動による光学性能の劣化(倍率色収差と呼ぶ)を考慮しなくて済むんですよ。 | |
 | でも、主流じゃないですよね?? | |
 | ¥(f¥theta¥)レンズと比べると、入射ビームを斜めに反射させる必要があるので、どうしても収差が大きくなるデメリットがありますからね。 | |
 | う〜ん、積極的に使いたいとは思えないですけど。 | |
 | 光線が折りたためるから、小型化には有利です。だから、A4サイズの機種には、よく使われますね。 | |
 | これも結局、適材適所って話ですね。 |
〜エネルギー保存則、破れたり〜
 | 教授。私、凄いこと発見しちゃいました。 | |
 | 何でしょう?? | |
 | 例えば、 ¥[ I = A ¥sin ¥omega t ¥] と書ける波動があったとしますよね。 | |
 | はい。 | |
 | こういう波動を2つ合成したら、 ¥[ I^{¥thinspace ¥prime} = A ¥sin ¥omega t + A ¥sin ¥omega t = 2 A ¥sin ¥omega t ¥tag{3.2.24} ¥] になりますよね。 | |
 | そうですね。 | |
 | 合成前のエネルギーは¥(A^2+A^2=2A^2¥)だけど、合成後のエネルギーは¥(¥left(2A¥right)^2=4A^2¥)になるから、波動の合成ではエネルギー保存則が成立しないんですよ〜。凄くないですか?? | |
 | なるほど。 | |
 | あれ??あんまり驚いてないですね…。 | |
 | 確かに、素粒子物理学の世界では、パリティ対称性が破れたり、CP対称性が破れたりしますから、いろいろな法則が成立しない条件があってもおかしくないでしょうが、まぁ、他のすべての法則に反証が見つかったとしても、エネルギー保存則だけは最後の最後まで守られると思いますよ。 | |
 | でも、波動では成立しないじゃないですか。 | |
 | 数式上はそう見えるっていうだけの話です。 | |
 | ムムム。 | |
 | 例えば、Youngの干渉実験を思い出してください。確かに合成した結果、4倍のエネルギーとなる場所もありましたが、打ち消しあって0倍になる場所もありましたよね。つまり、平均的には2倍となって、エネルギー保存則は成立しています。 | |
 | あれは合成したと言っても、2つの穴を通過した光が干渉したものじゃないですか。そうじゃなくて、完全に重ね合わせるってことですよ。 | |
 | なるほど。 | |
 | その場合は、強め合ったり弱め合ったりすることがないでしょ?? | |
 | そうですが、残念ながら、そういう実験系を組むことはできません。 | |
 | ん??できない?? | |
 | はい。式3.2.24が示しているのは、エネルギー保存則が成立しないということではなく、そういう式を満たすような実験系は組めないということなんです。 | |
 | 永久機関みたいなもの?? | |
 | う〜ん、できそうでできない、という意味では同じ仲間かもしれません。完全に重ね合わせるには、合成する素子が必要になりますよね?? | |
 | 例えば、ハーフミラーのような素子ですね。 | |
 |
そうです。しかし、ハーフミラーだと、入射する光のうち半分は別の光路に導かれるので、合成される光はそれぞれ1/2です。
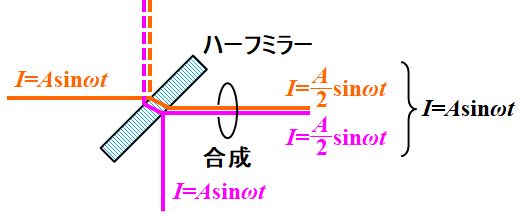 図3.2.41 エネルギー保存則、破れる?? だから、 ¥[ I^{¥thinspace ¥prime} = ¥frac{A}{2} ¥sin ¥omega t + ¥frac{A}{2} ¥sin ¥omega t = A ¥sin ¥omega t ¥] となって、エネルギーは¥(A^2¥)です。 |
|
 | あれ??入射したときは¥(2A^2¥)だから減ってる?? | |
 | もう1つの光路の分があるから、結局¥(2A^2¥)になります。 | |
 | じゃぁ、PBSだったら?? | |
 | ¥(p¥)偏光の光と¥(s¥)偏光の光を合成しても干渉は起こりません。つまり、そもそも式3.2.26が成立しないです。 | |
 | う〜ん。他に巧い方法ないかな〜。 | |
 | 思考の遊戯として、あれこれ思い巡らすのはいいですけど、考えるだけ無駄ですね。 | |
 | え〜。せっかく、凄い発見だと思ったのに〜。 | |
 | 残念ですが、物理の法則をひっくり返すのは並大抵ではないですよ。 | |
 | でも、もしひっくり返したらノーベル賞ですよね。 | |
 | ひっくり返したら、ですけど。 | |
 | だったら、私は諦めませんよ!! | |
 | …。 |
| 前頁へ | 戻る | 次頁へ |