 | さて、式1.1.13について、空間の2階微分を計算してください。 \[ u \big( \vec{\mathstrut r},t \big) = A \exp \Big[ i \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \big) \Big] \tag{1.1.13} \] | |
 | 空間の??2階微分?? | |
 | 要するに、\(\vec{\mathstrut r}=(x,y,z)\)の各成分で2階微分すればいいんです。 | |
 | う〜ん。やっぱり数学するのかぁ。じゃ、まず\(x\)について―。 \[ \frac { \partial u }{ \partial x} = i k_x A \exp \Big[ i \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \big) \Big] \] これが1階微分だから…。 \[ \frac { \partial ^2 u }{ \partial x ^2 } = -{k_x}^2 A \exp \Big[ i \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \big) \Big] = -{k_x}^2 u \] こうだな。 | |
 | \(y\)と\(z\)は\(x\)と交換可能だから、計算不要でしょう。そうすると、 \[ \left( \frac { \partial ^2 }{ \partial x ^2 } + \frac { \partial ^2 }{ \partial y ^2 } + \frac { \partial ^2 }{ \partial z ^2 } \right) u = - \left( {k_x}^2 + {k_y}^2 + {k_z}^2 \right) u \] となります。ここで、 \[ \nabla ^2 \equiv \frac { \partial ^2 }{ \partial x ^2 } + \frac { \partial ^2 }{ \partial y ^2 } + \frac { \partial ^2 }{ \partial z ^2 } \] という記号を導入しましょう。 | |
 | ナブラ(\(\nabla\))ですね。 | |
 | そうです。ギリシャ語で竪琴という意味ですが、記号の形が似ているので、そのように呼ばれます。ちなみに、\(\nabla\)の2乗(\(\nabla^2=\nabla\cdot\nabla\))はラプラシアンと言ったりもします。それと、 \[ {k_x}^2 + {k_y}^2 + {k_z}^2 = \vec{\mathstrut k^2} = k^2 \] はいいですね?? | |
 | あ、そうか。ベクトルの長さ(の2乗)ですもんね。そうすると、 \[ \nabla ^2 u = -k^2 u \tag{1.2.1} \] ってことか。 | |
 | 次は、時間の2階微分です。 | |
 | え〜っと。 \[ \frac { \partial u }{ \partial t} = -i \omega \exp \Big[ i \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi _0 \big) \Big] \] これが1階微分だから…。 \[ \frac { \partial ^2 u }{ \partial t ^2 } = - \omega ^2 u \tag{1.2.2} \] こうか。 | |
 | で、式1.2.1を式1.2.2で割ります。 | |
 | えいっ!! \[ \nabla ^2 u = \frac{ k^2 } { \omega ^2 } \frac{ \partial ^2 u }{ \partial t ^2 } \] | |
 | 係数の部分は、式1.1.9と式1.1.10を使えば、 \[ \frac{ k } { \omega } = \cfrac{ \cfrac{2 \pi}{\lambda} } { \cfrac{2 \pi}{T} } = \frac{ T } { \lambda } \] ですし、更に式1.1.7を使うと、 \[ \frac{ T } { \lambda } = \frac{1}{v_p} \] ですから―。 | |
 | こうですね。 \[ \nabla ^2 u = \frac{ 1 } { {v_p} ^2 } \frac{ \partial ^2 u }{ \partial t ^2 } \tag{1.2.3} \] | |
 |
この式を古典的波動関数、或いはHelmholtz方程式と言ったりします。
 Ferdinand von Helmholtz(1821〜1894) 尤も、数学的には式1.2.1の「楕円型の偏微分方程式」を指してHelmholtz方程式と言いますけどね。物理学的には、式1.2.3をHelmholtz方程式と呼んでも差し支えないでしょう。 |
|
 | 何か、怖そうな人ですね…。 | |
 | Helmholtzは、元々は生理学者です。子供の頃、病弱だったために、医者の道を志すんですが、経済的な理由から大学へは進まず、軍医になるために王立医学研究所に入所します。ただ、Helmholtzにとっては、この選択はラッキーで、この研究所にはたいへん優れた先生が集まっており、その人たちの薫陶を受けて、めきめきと才能を開花させていきます。で、色の三原色の理論、色盲、音と聴覚の研究、流体力学の分野で業績を挙げて、しかも独学で数学を勉強して、物理学の重要法則であるエネルギー保存則を完成させるんです。 | |
 | 数学を独学とは!! | |
 | とにかく、その研究分野は幅広くて、大変な才能の持ち主だったわけです。こうして、ドイツ科学界の重鎮として君臨することになり、多くの優れた弟子を輩出したことでも有名です。 | |
 | へぇ。凄いですね〜。 | |
 | この微分方程式は非常に重要で、波動は必ずこの方程式に帰着されます。逆に、このタイプの方程式が出てきたら、それは波動を意味しているのだと解釈して構いません。 | |
 | 教授。ひょっとして、本当は式1.2.3から出発して式1.1.13を導かないといけなかったのでは?? | |
 | そうですね。通常の物理学の教科書では、そういう筋書きで説明されていると思います。しかし、正統派の説明の方が遠まわりですし、このサイトの読者は、ある程度の学識を持っていることが期待できるので、少し亜流の説明に変えました。 | |
 | なるほど。 |
〜球面波の導出〜
 | さて、式1.2.3からは、平面波を示す式1.1.13だけでなく、極座標系で解くことにより球面波を示す式を導くこともできます。 | |
 | 極座標系?? | |
 |
通常のDescartes座標系では、直交する3つの軸\((x,y,z)\)を使って空間上の1点を指示しますが、図1.2.1のようなパラメータ\((r,\theta,\phi)\)を使っても空間上の1点を指示できるでしょ??
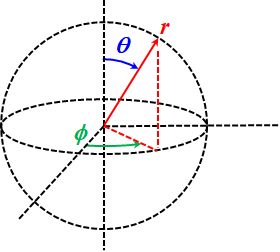 図1.2.1 極座標系 これが極座標系です。 |
|
 | つまり、どの方向を見ているかを\(\theta\)と\(\phi\)で決めて、観測点からの距離\(r\)を加味して空間上の1点を指示するわけですね。 | |
 | このとき、 \[ r = \sqrt{ x^2 + y^2 + z^2 } \tag{1.2.4} \] が成立します。 | |
 | Pythagorasの定理ですね。 | |
 | そうすると、こんな計算式が成立します。 \[ \frac{ \partial u }{ \partial x } = \frac{ \partial u }{ \partial r } \frac{ \partial r }{ \partial x } = \frac{ \partial u }{ \partial r } \frac{ x }{ \sqrt{ x^2 + y^2 + z^2 } } = \frac{ x }{ r } \frac{ \partial u }{ \partial r } \tag{1.2.5} \] では、覚悟はいいですか?? | |
 | え??か、覚悟?? | |
 | これを\(x\)で再び微分してください。 | |
 | え〜。面倒な計算を私に押し付けてるじゃないですか〜。 | |
 | そんなに難しくありませんよ。 | |
 | しょうがないなぁ。ん〜と…。 \[ \begin{align*} \frac{ \partial ^2 u }{ \partial x ^2 } &= \frac{ \partial }{ \partial x } \left( \frac{ \partial u }{ \partial x } \right) = \frac{ \partial }{ \partial x } \left( \frac{ x }{ r } \frac{ \partial u }{ \partial r } \right) = \frac{ 1 }{ r } \frac{ \partial u }{ \partial r } + \frac{x}{r} \frac{ \partial }{ \partial x } \left( \frac{ \partial u }{ \partial r } \right) \\ &= \frac{ 1 }{ r } \frac{ \partial u }{ \partial r } + \frac{x}{r} \frac{ \partial }{ \partial r } \left( \frac{ \partial u }{ \partial x } \right) \end{align*} \] 最後に、\(\cfrac{\partial u}{\partial x}\)が出てきましたけど、式1.2.5を代入してもいいですか?? | |
 | どうぞ。 | |
 | 結構、大変だなぁ。 \[ \begin{align*} \frac{ \partial ^2 u }{ \partial x ^2 } &= \frac{ 1 }{ r } \frac{ \partial u }{ \partial r } + \frac{x}{r} \frac{ \partial }{ \partial r } \left( \frac{ x }{ r } \frac{ \partial u }{ \partial r } \right) = \frac{ 1 }{ r } \frac{ \partial u }{ \partial r } + \frac{x}{r} \left( - \frac{ x }{ r^2 } \frac{ \partial u }{ \partial r } + \frac{ x }{ r } \frac{ \partial ^2 u }{ \partial r^2 } \right) \\ &= \frac{ r^2 - x^2 }{ r^3 } \frac{ \partial u }{ \partial r } + \frac{ x^2 }{ r^2 } \frac{ \partial ^2 u }{ \partial r^2 } \end{align*} \] これ、合ってるのかなぁ。 | |
 | 恐らく大丈夫だと思いますが、このサイトの執筆者も慣れないLaTexを使って書いているので、ヒヤヒヤしているようです。 | |
 | 読者のチェックも期待できそうにないですしね。 | |
 | 書いてみたものの、かなり後悔しているとも言ってましたね。しかし、ここまでくれば、\(y\)と\(z\)は\(x\)と交換可能だから、 \[ \begin{align*} \nabla ^2 u &= \frac{ 3r^2 - \left( x^2 + y^2 + z^2 \right) }{ r^3 } \frac{ \partial u }{ \partial r } + \frac{ x^2 + y^2 + z^2 }{ r^2 } \frac{ \partial ^2 u }{ \partial r^2 } \end{align*} \] となるのは分かりますね?? | |
 | あれ??式1.2.4が適用できそうですよ。 | |
 | はい。ですので、 \[ \begin{align*} \nabla ^2 u = \frac{ 3r^2 - r^2 }{ r^3 } \frac{ \partial u }{ \partial r } + \frac{ r^2 }{ r^2 } \frac{ \partial ^2 u }{ \partial r^2 } = \frac{ 2 }{ r } \frac{ \partial u }{ \partial r } + \frac{ \partial ^2 u }{ \partial r^2 } = \frac{ 1 }{ r } \frac{ \partial ^2 \left( ru \right) }{ \partial r^2 } \tag{1.2.6} \end{align*} \] | |
 | ムムム。最後、何かコワザ使いましたね?? | |
 | 逆算してみれば、合ってるかどうか確認できますよ。 | |
 | どれどれ。 \[ \begin{align*} \frac{ 1 }{ r } \frac{ \partial ^2 \left( ru \right) }{ \partial r^2 } &= \frac{ 1 }{ r } \frac{ \partial }{ \partial r } \left[ \frac{ \partial \left( ru \right) }{ \partial r } \right] = \frac{ 1 }{ r } \frac{ \partial }{ \partial r } \left( u + r \frac{ \partial u }{ \partial r } \right) = \frac{ 1 }{ r } \left[ \frac{ \partial u }{ \partial r } + \frac{ \partial }{ \partial r } \left( r \frac{ \partial u }{ \partial r } \right) \right] \\ &= \frac{ 1 }{ r } \left( \frac{ \partial u }{ \partial r } + \frac{ \partial u }{ \partial r } + r \frac{ \partial ^2 u }{ \partial r^2 } \right) = \frac{ 1 }{ r } \left( 2 \frac{ \partial u }{ \partial r } + r \frac{ \partial ^2 u }{ \partial r^2 } \right) = \frac{ 2 }{ r } \frac{ \partial u }{ \partial r } + \frac{ \partial ^2 u }{ \partial r^2 } \end{align*} \] お〜。同じになった。 | |
 | という確認ができたところで、式1.2.6を式1.2.3に代入します。 \[ \begin{align*} \frac{ 1 }{ r } \frac{ \partial ^2 \left( ru \right) }{ \partial r^2 } = \frac{ 1 } { {v_p} ^2 } \frac{ \partial ^2 u }{ \partial t ^2 } \quad \Leftrightarrow \quad \frac{ \partial ^2 \left( ru \right) }{ \partial r^2 } = \frac{ 1 } { {v_p} ^2 } \frac{ \partial ^2 \left( ru \right) }{ \partial t ^2 } \end{align*} \] | |
 | すっきりしましたね。 | |
 | 式1.2.3と見比べてみてください。 | |
 | \(ru\)という関数が、Helmholtz方程式を満たしている、ってことですね。 | |
 | そして、その解は式1.1.13で与えられていたので、 \[ ru = A \exp \big[ i \left( kr - \omega t + \phi _0 \right) \big] \] です。極座標系では、\(r\)はベクトルじゃなくなる点に注意してください。 | |
 | ってことは、 \[ u \left( r \right) = \frac{ A }{ r } \exp \big[ i \left( kr - \omega t + \phi _0 \right) \big] \tag{1.2.7} \] かな?? | |
 |
これが球面波の一般式です。球面波は、こんな波動ですね。
|
|
 | 馴染み深い波紋ですね。 | |
 | 式1.2.7は、回折を勉強するときに登場するので、覚えておきましょう。 |
| 前頁へ | 戻る | 次頁へ |