 |
いよいよ回折の章に突入です。回折を初めて詳細に取り上げたのはGrimaldiと言われています。
 Francesco Maria Grimaldi(1618~1663) |
|
 |
回折って、こんな現象ですね??
|
|
 | はい。いわゆる、波動のまわり込み現象のことです。干渉と比較すると、光でも回折は身近な現象として目にすることが多いと思います。 | |
 | 回折も波動特有の現象ですね。 | |
 |
波動の伝搬の様子については、それを作図的に示すHuygensの原理があります。
 Christiaan Huygens(1629~1695) |
|
 | 作図的?? | |
 |
波動の様子を理解するためのテクニック(論文)ですね。まず、ある波面Σを考えます。
 図4.1.1 Huygensの原理(1) 次に、その波面Σの上に無数の仮想的な波源が乗っているとするのです。 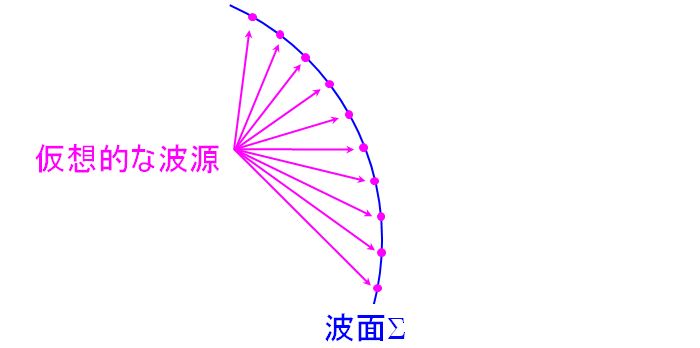 図4.1.2 Huygensの原理(2) そして、各波源から第2次波が発生していると考えます。 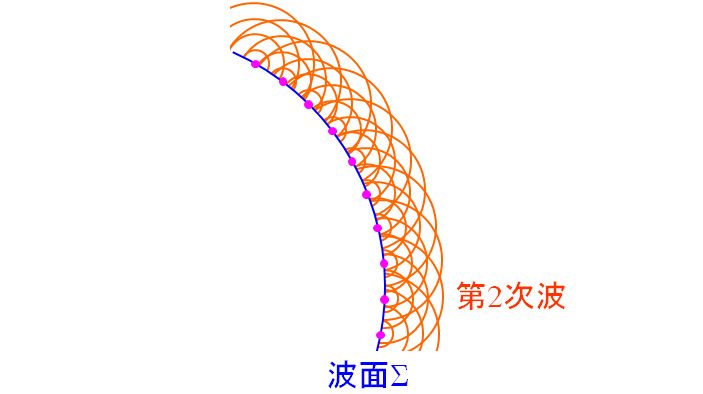 図4.1.3 Huygensの原理(3) 最後に、その包絡線を引けば、それが新しい波面Σ'となる、という手続きになります。  図4.1.4 Huygensの原理(4) |
|
 | へぇ。それで反射とか屈折も説明できるわけですね。 | |
 | それどころか、屈折率の均一な媒質中を伝搬する光が直進することとか、干渉とかも説明できます。 | |
 | ムムム。教授。ちょっと気が付いたんですけど、この方法、おかしいですよ。 | |
 | そうですか?? | |
 |
だって、第2次波の包絡線って、もう1本引けません??
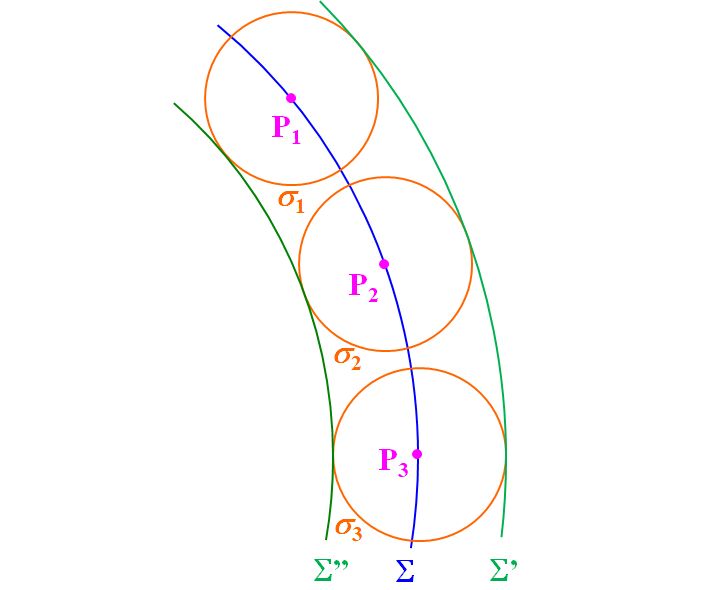 図4.1.5 後進波の謎 でも、実際の波動は、こういう後進する波面Σ"は存在しないじゃないですか。 |
|
 | 鋭い指摘ですね。同じことは、Poissonによっても疑問が出されました。 | |
 | お、私はPoissonと同じレベルだ~。 | |
 | しかし、その修正案はFresnelによって提示されました。 | |
 | また出たな、Fresnel!! | |
 | Fresnelの発想は、包絡線という考え方を捨て、その代わりに、新しい波面Σ'上の任意の点Qにおける波動は、波面Σ上の無数にある仮想波源からの波動の総和であると考えたのです。 | |
 | 要するに、干渉しているってことですね。でも、これでは後進波の問題は解消されてませんよ。 | |
 | そこで、これを定式化するときに、ちょっとした仕掛けを用意しました。それが傾斜係数\(K\left(\chi\right)\)という考え方です。 | |
 | 傾斜係数?? | |
 |
まず、波面Σは光源Sから放射された波面であるとし、光源S~点P(波面Σ上の点)までの距離を\(r_0\)とすれば、点Pの波動は、
\[
U \left( {\rm P} \right) = \frac{ A \mathrm{e} ^{ikr_0} }{ r_0 } \tag{4.1.1}
\]
と書けます。ここで、\(A\)は振幅です。
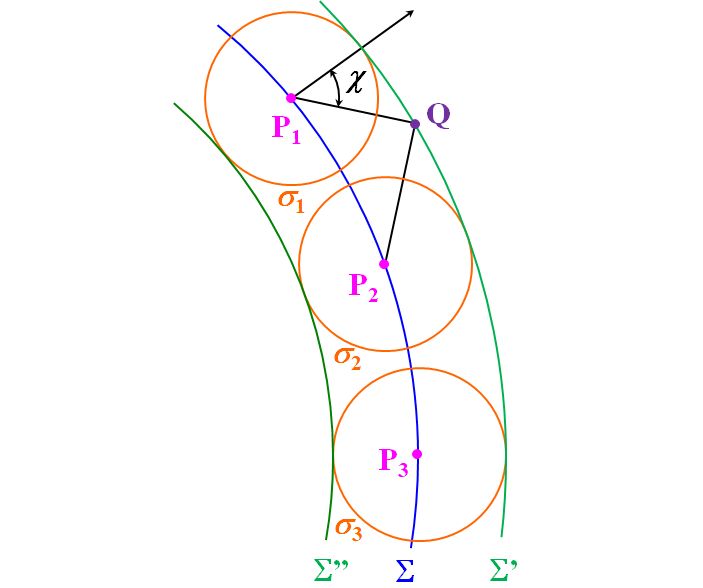 図4.1.6 傾斜係数 そのうえで、Huygens-Fresnelの原理を使い、波面Σ'上の点Qの波動\(U\left({\rm Q}\right)\)は、点Pの法線と、点Pと点Qを結ぶ線分とのなす角を\(\chi\)として、次のように定式化できる、としたのがFresnelのアイデアです(\(r\)は点Pと点Qの距離)。 \[ U \left( {\rm Q} \right) = \frac{ A \mathrm{e} ^{ikr_0} }{ r_0 } \iint_{\Sigma} K \left( \chi \right) \frac{ \mathrm{e} ^{ikr} }{ r } ds \tag{4.1.2} \] |
|
 | 点Pにおける微小面積\(ds\)の効果が寄せ集まったもの、ってことか…。ん??あれ??教授。傾斜係数は置いておくとして、式4.1.2の\({\displaystyle \iint_{\Sigma} \frac{ \mathrm{e} ^{ikr} }{ r } ds}\)って、点Qから放射した球面波を波面Σにわたって面積分しているように見えますね。 | |
 | よいところに気が付きました。\(r\)は、物理的な意味では点P~点Qまでの距離なんですが、数学的な手続きでは点Q~点Pまでの距離として取り扱われます。 | |
 | ってことは、\(r=0\)って、点Qのこと?? | |
 | 数学的な手続きでは、そうなりますね。実は、このことが、少し厄介な問題を生じます。 | |
 | 具体的には?? | |
 | それは、次回の講座で触れましょう。 | |
 | ふ~ん。で、傾斜係数っていうのは?? | |
 | Frenelの考えた傾斜係数は、 \[ \left\{ \ \begin{array}{l} K \left( \chi \right) = 1 \quad \quad \chi = 0 \\ K \left( \chi \right) = 0 \quad \quad \left| \chi \right| \geq \cfrac{ \pi }{2} \end{array} \right. \tag{4.1.3} \] というものです。 | |
 | う~ん。確かに、式4.1.3を導入すれば、後進波は計算上うまく消えてくれるかもしれないけど、いかにも作為的な感じがしますね。物理学的な意味があるようには思えないです。 | |
 | 確かに、傾斜係数の考え方はともかく、その関数の実体は別モノである可能性はありますね。そこで、回折現象を厳密に取り扱うことに挑戦する物理学者が登場します。 | |
 | 誰?? | |
 |
Kirchhoffです。
 Gustav Robert Kirchhoff(1824~1887) |
|
 | ん~。電気回路の任意の節点で、電流の総和が\(0\)になるとかいう法則を発見した人?? | |
 | Kirchhoffの第1法則ですね。Kirchhoffはロシアの物理学者です。よく知られている電気回路の法則以外にも音響学、弾性論、光学、黒体放射、分光学といった具合に、いろいろな分野に大きな功績を残しているんですよ。また、講義が大変に分かりやすいと評判だったようです。 | |
 | 教授とは真逆ですね~。 | |
 |
…。Kirchhoffの考え(論文)を理解するには、ベクトル解析の基本定理の1つであるGreenの定理から出発する(論文)必要があるんですが、いきなり理論的な話を始める前に、おおまかな攻略法だけ示しておきましょう。
 George Green(1793~1841) |
|
 | ということは、かなり難しいってことだなぁ、きっと。 | |
 |
はい。ちょっと取っ付きにくいかもしれません。流れは、次のようになっています。 ①Greenの定理の被積分関数が波動関数であると考えてゴリゴリ計算する ②厳密解としてHelmholtz-Kirchhoffの回折積分が求まる ③現実的なモデルを導入し、近似計算するとFresnel-Kirchhoffの回折積分が計算される ④スクリーン上に現れる回折パターンを計算し、2種類の回折の公式を導出する |
|
 | 何で2種類なんですか?? | |
 | 近似のレベルが違うんですよ。 | |
 | 道のりが長そうですね。 | |
 | では、次回から回折理論に突入しましょう。 | |
 | 今回の予告編が藪蛇になりませんように…。 |
| 前頁へ | 戻る | 次頁へ |