 | Kirchhoffは式4.1.2を見て、点Qに集まる波動の情報は、より一般的には点Qを取り囲むすべての空間からやってくると考えました。そして、その考えに基づいて傾斜係数の正体を理論的に議論しようとしたのです。 | |
 | 一般化した方が問題の見通しがよくなるなんて、不思議ですね。 | |
 |
まず、Greenの定理の復習から取り掛かりましょう。
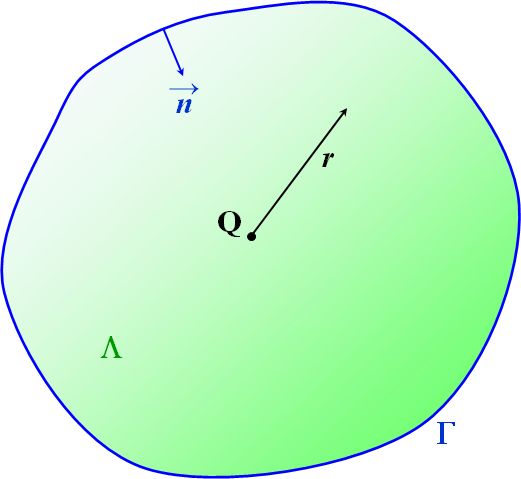 図4.1.7 Greenの定理(1) この定理は、閉曲面\(\Gamma\)で囲まれた3次元空間内の領域\(\Lambda\)、2階微分可能な任意のスカラー関数\(U\)、\(V\)について、 \[ \iiint_{\Lambda} \left( U \nabla^2 V - V \nabla^2 U \right) d \Lambda = - \iint_{\Gamma} \left( U \frac{\partial V}{\partial n} - V \frac{\partial U}{ \partial n} \right) d \Gamma \tag{4.1.4} \] が成立する、というものです。\(n\)は、領域\(\Lambda\)の内向きの法線ベクトルで、単位ベクトルとします。 |
|
 | う~ん、何だかよく分からないけど、要するに体積分を面積分に変換する公式ってことですね。 | |
 | ここで、\(U\)を光波を表す波動関数と考えます。そうすると、\(U\)は式1.2.1を満たさないといけないので、 \[ \left( \nabla^2 + k^2 \right) U = 0 \tag{4.1.5} \] です。次に、Huygensの原理に基づき、\(V\)として\(\Lambda\)内の1点Qに伝搬する球面波を考え、 \[ V = \frac{\mathrm{e}^{ikr}}{r} \tag{4.1.6} \] としましょう。\(r\)は、仮想的な波源~点Qまでの距離です。 | |
 | \(V\)だって式1.2.1を満たさないといけないですよね?? \[ \left( \nabla^2 + k^2 \right) V = 0 \tag{4.1.7} \] | |
 | そうですね。そうすると、\(U\)と\(V\)を波動関数と考えた場合には、Greenの定理の左辺は\(0\)になってしまいます。 \[ \iint_{\Gamma} \left( U \frac{\partial V}{\partial n} - V \frac{\partial U}{ \partial n} \right) d \Gamma = 0 \tag{4.1.8} \] | |
 | お~、それはいい!! | |
 | 式4.1.8は\(\Gamma\)上の面積分を表しているわけですが、このとき、\(U\)は\(\Gamma\)にへばりついた波動関数であり、\(V\)の方は\(\Gamma\)上にある任意の点を波源とした球面波と捉え直すことができます。 | |
 | Huygens-Fresnelの原理がそっくりそのまま展開されているわけですね。 | |
 | さて、ここで式4.1.8に式4.1.6を代入するんですが、1つだけ注意点があります。 | |
 | 注意点?? | |
 | このとき思い出してほしいんですが、前回の講座で、式4.1.6で表現される球面波は、数学的には「点Qから放射されたもの」として取り扱うという話をしました。 | |
 | その指摘したの、私で~す。だから、\(r=0\)とは点Qのこと、ですよね?? | |
 | はい。そのときに、それは少し厄介な問題を引き起こすという話もしました。 | |
 | あ、そう言えば、そうですね。 | |
 | 実は、Greenの定理は、それぞれの関数\(U\)、\(V\)が\(\Lambda\)内で連続でないといけない、というルールがあります。 | |
 | まぁ、たいていの公式って、対象としている関数は連続で微分可能、っていうのが前提になってますよ。 | |
 | しかし、式4.1.6は点Qにおいて\(r=0\)なので、\(V\rightarrow\infty\)になってしまいます。 | |
 | ムムム。点Qは特異点ってことか。そしたら、それ以上どうにもならないじゃないですか。 | |
 |
こういう場合には、上手いテクニックがあります。それは、点Qを除くように、点Qを中心とする半径\(\varepsilon\)の球面\(\Gamma^{\thinspace \prime}\)を考えて、\(\Lambda\)を\(\Gamma\)と\(\Gamma^{\thinspace \prime}\)で挟まれた空間と定義するのです。
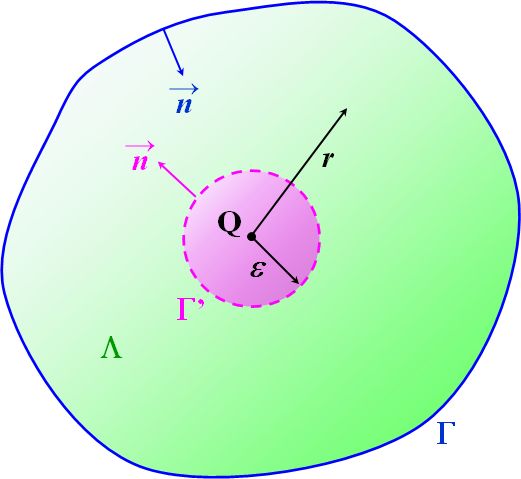 図4.1.8 Greenの定理(2) |
|
 | でも、\(\Gamma^{\thinspace \prime}\)の内側の空間は除かれたままだから、抜本的な解決になってないですよ。 | |
 | 後で\(\varepsilon\rightarrow 0\)という極限をとってやるんです。 | |
 | う~ん、それでも結果が発散しちゃったら、元の木阿弥ですけど。 | |
 | ま、やっていけば分かります。 | |
 | ふ~ん、お手並み拝見ってところですね。 | |
 | まず、新しい空間\(\Lambda\)で式4.1.8を書き直しましょう。 \[ \begin{align*} &\iint_{\Gamma} \left[ U \frac{\partial}{\partial n} \left( \frac{\mathrm{e}^{ikr}}{r} \right) - \frac{\mathrm{e}^{ikr}}{r} \frac{\partial U}{ \partial n} \right] d \Gamma \\ &\quad \quad \quad \quad \quad \quad \quad \quad + \iint_{\Gamma^{\thinspace \prime}} \left[ U \frac{\partial}{\partial n} \left( \frac{\mathrm{e}^{ik r}}{r} \right) - \frac{\mathrm{e}^{ik r}}{r} \frac{\partial U}{ \partial n} \right] d \Gamma^{\thinspace \prime} = 0 \tag{4.1.9} \end{align*} \] | |
 | 教授。式4.1.9の左辺の第2項って、点Qを中心とする半径\(\varepsilon\)の球面(=\(\Gamma^{\thinspace \prime}\))で面積分するんだから、\(r=\varepsilon\)になりませんか?? | |
 | そうですね。ついでに言えば、\(\Gamma^{\thinspace \prime}\)の法線\(n\)の方向と\(\varepsilon\)も一致します。つまり、 \[ \frac{\partial}{\partial n} = \frac{\partial }{ \partial \varepsilon} \tag{4.1.10} \] です。以上のことを踏まえれば、 \[ \begin{align*} &\iint_{\Gamma} \left[ U \frac{\partial}{\partial n} \left( \frac{\mathrm{e}^{ikr}}{r} \right) - \frac{\mathrm{e}^{ikr}}{r} \frac{\partial U}{ \partial n} \right] d \Gamma \\ &\quad \quad \quad \quad \quad \quad \quad \quad + \iint_{\Gamma^{\thinspace \prime}} \left[ U \frac{\partial}{\partial \varepsilon} \left( \frac{\mathrm{e}^{ik \varepsilon}}{\varepsilon} \right) - \frac{\mathrm{e}^{ik \varepsilon}}{\varepsilon} \frac{\partial U}{ \partial \varepsilon} \right] d \Gamma^{\thinspace \prime} = 0 \tag{4.1.11} \end{align*} \] となります。 | |
 | なるほど。 | |
 | 式4.1.11の左辺の第2項の\(U\)は\(\Gamma^{\thinspace \prime}\)にへばりついた波動関数ですから、もし\(\varepsilon\rightarrow 0\)という操作で積分の結果が収束すれば、\(U\)は限りなく点Qに近づくので、それこそ我々の知りたい\(U\left({\rm Q}\right)\)となることが期待できますよね?? | |
 | 収束すれば、ですけど。 | |
 | 次に、\(d\Gamma^{\thinspace \prime}\)は立体角\(\Omega\)を使って、 \[ d \Gamma^{\thinspace \prime} = \varepsilon^2 d \Omega \tag{4.1.12} \] と書けます。 | |
 | そうすると、式4.1.11の左辺の第2項は、 \[ \begin{align*} &\iint_{\Gamma^{\thinspace \prime}} \left[ U \frac{\partial}{\partial \varepsilon} \left( \frac{\mathrm{e}^{ik \varepsilon}}{\varepsilon} \right) - \frac{\mathrm{e}^{ik \varepsilon}}{\varepsilon} \frac{\partial U}{ \partial n} \right] \varepsilon^2 d \Omega \\ &\quad \quad \quad \quad \quad \quad = \iint_{\Gamma^{\thinspace \prime}} \left[ U \left( ik \frac{\mathrm{e}^{ik \varepsilon}}{\varepsilon} - \frac{\mathrm{e}^{ik \varepsilon}}{\varepsilon^2} \right) - \frac{\mathrm{e}^{ik \varepsilon}}{\varepsilon} \frac{\partial U}{ \partial n} \right] \varepsilon^2 d \Omega \\ &\quad \quad \quad \quad \quad \quad = \iint_{\Gamma^{\thinspace \prime}} \left[ U \left( ik \varepsilon \mathrm{e}^{ik \varepsilon} - \mathrm{e}^{ik \varepsilon} \right) - \varepsilon \mathrm{e}^{ik \varepsilon} \frac{\partial U}{ \partial n} \right] d \Omega \tag{4.1.13} \end{align*} \] ですね。 | |
 | \(\varepsilon\rightarrow 0\)としてみてください。 | |
 | お!! \[ \begin{align*} &\lim_{\varepsilon \to 0} \iint_{\Gamma^{\thinspace \prime}} \left[ U \left( ik \varepsilon \mathrm{e}^{ik \varepsilon} - \mathrm{e}^{ik \varepsilon} \right) - \varepsilon \mathrm{e}^{ik \varepsilon} \frac{\partial U}{ \partial n} \right] d \Omega \\ &\quad \quad \quad \quad \quad \quad = -U\left({\rm Q}\right)\iint_{\Gamma^{\thinspace \prime}} d \Omega = - 4 \pi U\left({\rm Q}\right) \tag{4.1.14} \end{align*} \] になった。 | |
 | よって、式4.1.11は、 \[ \begin{align*} &\iint_{\Gamma} \left[ U \frac{\partial}{\partial n} \left( \frac{\mathrm{e}^{ikr}}{r} \right) - \frac{\mathrm{e}^{ikr}}{r} \frac{\partial U}{ \partial n} \right] d \Gamma - 4 \pi U \left( {\rm Q} \right) = 0 \\ &\quad \quad \quad \Leftrightarrow \quad U \left( {\rm Q} \right) = \frac{1}{4 \pi } \iint_{\Gamma} \left[ U \frac{\partial}{\partial n} \left( \frac{\mathrm{e}^{ikr}}{r} \right) - \frac{\mathrm{e}^{ikr}}{r} \frac{\partial U}{ \partial n} \right] d \Gamma \tag{4.1.15} \end{align*} \] と書けるわけです。式4.1.15をHelmholtz-Kirchhoffの回折積分と言います。 | |
 | ここまでは厳密解として計算できるのかぁ。 |
~衝立に穴を開けたときの回折~
 | でも、式4.1.15は、Fresnelの提示した式4.1.2とは程遠い気がしますね。 | |
 |
そこで、少し具体的な例で応用させてみましょう。回折で一番簡単なモデルは、衝立Dに孔を開け、そこに光源Sからの光を通過させるというものです。
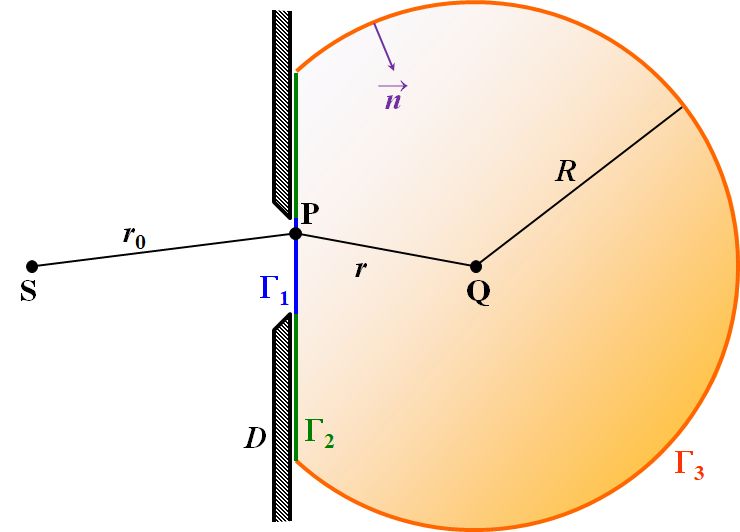 図4.1.9 Kirchhoffの回折積分(1) |
|
 | 確かに。 | |
 | このとき、点Qを囲む閉曲面が3つに分解できるのは分かりますか?? | |
 | ん~、1つは孔のところで\(\Gamma_1\)かな。それと孔以外の衝立部分\(\Gamma_2\)、それと空間を取り囲む\(\Gamma_3\)ですね。 | |
 |
まず、\(\Gamma_1\)と\(\Gamma_2\)について、次のような仮定を設定します。それは、 ①\(\Gamma_1\)における\(U\)及び\(\cfrac{\partial U}{\partial n}\)は衝立があってもなくても変化しない ②\(\Gamma_2\)における\(U\)及び\(\cfrac{\partial U}{\partial n}\)は\(0\)である というものです。これをKirchhoffの境界条件と言います。 |
|
 | そんなに無理のある仮定だとは思いませんけど。 | |
 | そうですね。光の波長に比べて孔の大きさが充分大きい場合には非常によい近似となります。次は\(\Gamma_3\)です。 | |
 | う~ん、直感的には、\(\Gamma_3\)の情報は点Qからすれば後進波に見えるから\(0\)になりそうな気がしますけど。 | |
 | なかなか鋭いですね。確認してみましょう。 | |
 | 式4.1.15を利用するんだったら、\(\Gamma_3\)は、点Qを中心とした球面というふうに考えると計算が楽そうです。 | |
 | なるほど。その半径を\(R\)と置けば、式4.1.10と同じように、 \[ \frac{\partial}{\partial n} = \frac{\partial }{ \partial R} \tag{4.1.16} \] とできますからね。 | |
 | そうすると…。 \[ \begin{align*} U\left({\rm Q} \right) &= \frac{1}{4 \pi } \iint_{\Gamma_3} \left[ U \frac{\partial}{\partial R} \left( \frac{\mathrm{e}^{ikR}}{R} \right) - \frac{\mathrm{e}^{ikR}}{R} \frac{\partial U}{ \partial R} \right] d \Gamma_3 \\ &= \frac{1}{4 \pi } \iint_{\Gamma_3} \left[ U \left( ik \frac{\mathrm{e}^{ikR}}{R} - \frac{\mathrm{e}^{ikR}}{R^2} \right) - \frac{\mathrm{e}^{ikR}}{R} \frac{\partial U}{ \partial R} \right] R^2 d \Omega \\ \tag{4.1.17} \end{align*} \] かな。 | |
 | 式4.1.17の被積分関数の第1項について見てみると、\(R\rightarrow\infty\)としても\(\mathrm{e}^{ikR}\)が発散することはありませんから、 \[ ik \frac{\mathrm{e}^{ikR}}{R} - \frac{\mathrm{e}^{ikR}}{R^2} = \left( ik - \frac{1}{R} \right) \frac{\mathrm{e}^{ikR}}{R} \tag{4.1.18} \] として、\(R\rightarrow\infty\)のとき\(ik \cfrac{\mathrm{e}^{ikR}}{R}\)に近似できることが分かります。 | |
 | つまり、式4.1.17は、 \[ \begin{align*} U\left( {\rm Q} \right) &= \frac{1}{4 \pi } \iint_{\Gamma_3} \left[ ikU \frac{\mathrm{e}^{ikR}}{R} - \frac{\mathrm{e}^{ikR}}{R} \frac{\partial U}{ \partial R} \right] R^2 d \Omega \\ &= \frac{1}{4 \pi } \iint_{\Gamma_3} R \left( ikU - \frac{\partial U}{ \partial R} \right) \mathrm{e}^{ikR} d \Omega \tag{4.1.19} \end{align*} \] になるってことか。 | |
 |
というわけで、
\[
\displaystyle \lim_{R \to \infty} R \left( ikU - \frac{\partial U}{ \partial R} \right) =0 \tag{4.1.20}
\]
が満たされれば、式4.1.19が\(0\)になることが言えそうですね。式4.1.20はSommerfeldの放射条件と呼ばれます。
 Arnold Johannes Sommerfeld(1868~1951) |
|
 | 成立するかな…。 | |
 | \(\Gamma_3\)にへばりついている波動関数\(U\)が、点Qから放射された光波だとすると、式4.1.1で表される球面波と考えてよいので―。 | |
 | ん??その仮定は、ちょっと異議ありって感じですけど?? | |
 | この計算では\(R\rightarrow\infty\)を前提にしてますから、このとき点Qは衝立Dに限りなく近づきますし、孔の大きさも無限に小さくなります。そうすると、\(\Gamma_3\)にへばりついている\(U\)は、点Qからの球面波として見えるという考え方は、悪くない近似と思えませんか?? \[ U \approx \frac{ A \mathrm{e} ^{ikR} }{ R } \tag{4.1.21} \] | |
 | う~ん。強引な感じもしますけど。でも、有効な反論も思い付かないですね、悔しいけど…。 | |
 | この近似を認めて計算してみると、 \[ \begin{align*} R \left( ikU - \frac{\partial U}{ \partial R} \right) &= R \left[ ik \frac{A \mathrm{e}^{ikR}}{R} - \frac{\partial }{ \partial R} \left( \frac{A \mathrm{e}^{ikR}}{R} \right) \right] \\ &= R \left( ik \frac{A \mathrm{e}^{ikR}}{R} - ik \frac{A \mathrm{e}^{ikR}}{R} + \frac{A \mathrm{e}^{ikR}}{R^2} \right) = \frac{A \mathrm{e}^{ikR}}{R} \tag{4.1.22} \end{align*} \] となり―。 | |
 | \(R\rightarrow\infty\)でSommerfeldの放射条件を満たしそうですね。 | |
 | ということで、結局、点Qに対する波動は\(\Gamma_1\)からの寄与のみを考えればよいということが分かります。 \[ U \left( {\rm Q} \right) = \frac{1}{4 \pi } \iint_{\Gamma_1} \left[ U \frac{\partial}{\partial n} \left( \frac{\mathrm{e}^{ikr}}{r} \right) - \frac{\mathrm{e}^{ikr}}{r} \frac{\partial U}{ \partial n} \right] d \Gamma_1 \tag{4.1.23} \] | |
 | う~ん。\(\Gamma_1\)にへばりついている波動関数\(U\)は、光源Sからの球面波だから式4.1.1をそのまま使えるとしても、それ以上、計算の進めようがないような…。 | |
 | そんなことないですよ。方向微分係数が簡単に計算できるじゃないですか。 | |
 | 方向微分係数?? | |
 | つまり、ベクトル解析のイロハを忘れているわけですね。 | |
 | そうで~す。 | |
 | スカラー関数\(f\)に対し、\(d\vec{\mathstrut s}\)方向の単位ベクトルを\(\vec{\mathstrut e_s}\)としたとき、 \[ \frac{\partial f}{\partial s} = \vec{\mathstrut e_s} \nabla f = | \nabla f | \cos \psi \tag{4.1.24} \] が成立しますが、これを方向微分係数と呼ぶんです。\(\psi\)は、\(\vec{\mathstrut e_s}\)と\(\nabla f\)のなす角ですね。 | |
 | でも、\(U\)は球面波だから、\(\nabla U\)は極座標系で計算しないとダメですよね?? | |
 | ダメってことはないですが、極座標系で計算した方が便利ですね。極座標系\(\left(r,\theta,\phi\right)\)のとき、\(\nabla f\)は、 \[ \nabla f = \left( \frac{\partial f}{\partial r}, \quad \frac{1}{r}\frac{\partial f}{\partial \theta}, \quad \frac{1}{r \sin \theta} \frac{\partial f}{\partial \phi} \right) \tag{4.1.25} \] と書けます。 | |
 | ムムム。待てよ…。球面波だと、\(\theta\)成分も\(\phi\)成分も\(0\)だから、 \[ | \nabla f | = \frac{\partial f}{\partial r} \tag{4.1.26} \] では?? | |
 | 問題ありません。 | |
 |
しかも、その方向は、球面波の中心から点Pを結んだベクトルだから、
\[
\begin{align*}
\frac{\partial}{\partial n} \left( \frac{\mathrm{e}^{ikr}}{r} \right) &= \frac{\partial}{\partial r} \left( \frac{\mathrm{e}^{ikr}}{r} \right) \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r} \big) \\
&= \left( ik \frac{\mathrm{e}^{ikr}}{r} - \frac{\mathrm{e}^{ikr}}{r^2} \right) \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r} \big)
\approx ik \frac{\mathrm{e}^{ikr}}{r} \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r} \big) \tag{4.1.27}
\end{align*}
\]
\[
\begin{align*}
\frac{\partial U}{\partial n} &= \frac{\partial}{\partial n} \left( \frac{A \mathrm{e}^{ikr_0}}{r_0} \right) = \frac{\partial}{\partial r_0} \left( \frac{A \mathrm{e}^{ikr_0}}{r_0} \right) \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r_0} \big) \\
&= \left( ik \frac{A \mathrm{e}^{ikr_0}}{r_0} - \frac{A \mathrm{e}^{ikr_0}}{{r_0}^2} \right) \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r_0} \big)
\approx ik \frac{A \mathrm{e}^{ikr_0}}{r_0} \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r_0} \big) \tag{4.1.28}
\end{align*}
\]
ってことですね。
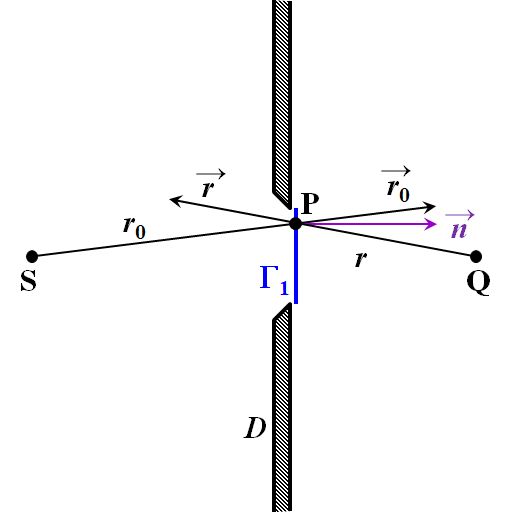 図4.1.10 Kirchhoffの回折積分(2) |
|
 | \(\vec{\mathstrut n}\)と\(\vec{\mathstrut r}\)のなす角を\(\big(\vec{\mathstrut n},\vec{\mathstrut r}\big)\)と書いたわけですね。そうすると、式4.1.23が書き直せませんか?? | |
 | ん~と。 \[ \begin{align*} U \left( {\rm Q} \right) &= \frac{1}{4 \pi } \iint_{\Gamma_1} \left[ \frac{A \mathrm{e}^{ikr_0}}{r_0} ik \frac{\mathrm{e}^{ikr}}{r} \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r} \big) - \frac{\mathrm{e}^{ikr}}{r} ik \frac{A \mathrm{e}^{ikr_0}}{r_0} \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r_0} \big) \right] d \Gamma_1 \\ &= \frac{1}{4 \pi } \iint_{\Gamma_1} ik \frac{A \mathrm{e}^{ik \left( r + r_0 \right) }}{rr_0} \Big[ \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r} \big) - \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r_0} \big) \Big] d \Gamma_1 \tag{4.1.29} \end{align*} \] かな。 | |
 | 式4.1.29をFresnel-Kirchhoffの回折積分と言います。 | |
 | でも、式4.1.2の形を目指したわりに、近づいた感じがしないですよ。 | |
 |
では、図4.1.10の\(\Gamma_1\)を、平面の代わりに、光源Sを中心とする球面で近似することにしましょう。
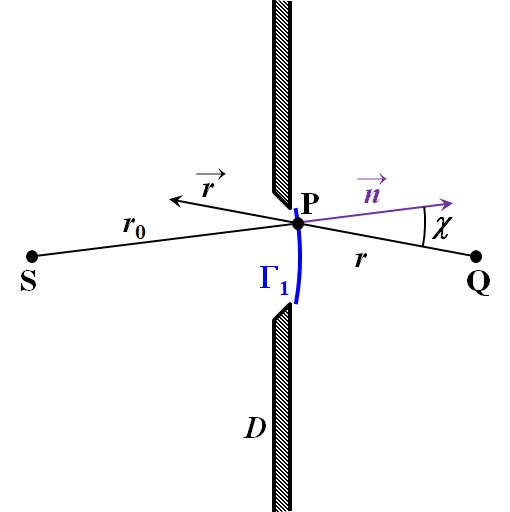 図4.1.11 Kirchhoffの回折積分(3) そうすると、 \[ \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r_0} \big) = 1 \tag{4.1.30} \] \[ \cos \big( \vec{\mathstrut n}, \vec{\mathstrut r} \big) = \cos \left( \pi - \chi \right) = - \cos \chi \tag{4.1.31} \] です。 |
|
 | お、ということは―。 \[ \begin{align*} U \left( {\rm Q} \right) &= \frac{1}{4 \pi } \iint_{\Gamma_1} ik \frac{A \mathrm{e}^{ik \left( r + r_0 \right) }}{rr_0} \left( - \cos \chi - 1 \right) d \Gamma_1 \\ &= - \frac{ik}{4 \pi } \frac{A \mathrm{e}^{ik r_0 }}{r_0} \iint_{\Gamma_1} \frac{\mathrm{e}^{ik r}}{r} \left( 1 + \cos \chi \right) d \Gamma_1 \tag{4.1.32} \end{align*} \] ですね。 | |
 | Fresnelの式と比較できませんか?? \[ U \left( {\rm Q} \right) = \frac{ A \mathrm{e} ^{ikr_0} }{ r_0 } \iint_{\Sigma} K \left( \chi \right) \frac{ \mathrm{e} ^{ikr} }{ r } ds \tag{4.1.2} \] | |
 | ムムム。傾斜係数の正体は、 \[ K \left( \chi \right) = - \frac{ik}{4 \pi } \left( 1 + \cos \chi \right) = - \frac{i}{2 \lambda } \left( 1 + \cos \chi \right) \tag{4.1.33} \] ってことか!! | |
 | 式4.1.33と式4.1.3を見比べると、Fresnelの予想とは違うことが分かりますね。 | |
 | そっか。\(\chi\)の範囲で\(K\)の値が\(0\)と\(1\)というふうに2値で決まるわけじゃなくて、\(\cos\chi\)に伴ってゆっくり変化するんですね。 | |
 | それと、\(-i\)があるということは、\(-i=\exp\left(-i\cfrac{\pi}{2}\right)\)なので、回折された波面は位相が\(\cfrac{\pi}{2}\)だけ進んでいることも分かります。 | |
 | なるほど。とは言うものの、Fresnelの予想も、いい線いってた、ってことですね。 | |
 | これで、任意の点Qにおける波動を議論する準備が整いました。では、次回はスクリーン上における回折パターンがどうなるかについて見ていくことにしましょう。 |
| 前頁へ | 戻る | 次頁へ |