 | ここからの議論は、いろいろと大胆な近似を行って議論していくことになります。 | |
 | 要するに、そうしないと問題が簡単にならないってことですね。 | |
 |
まず、座標を設定しましょう。
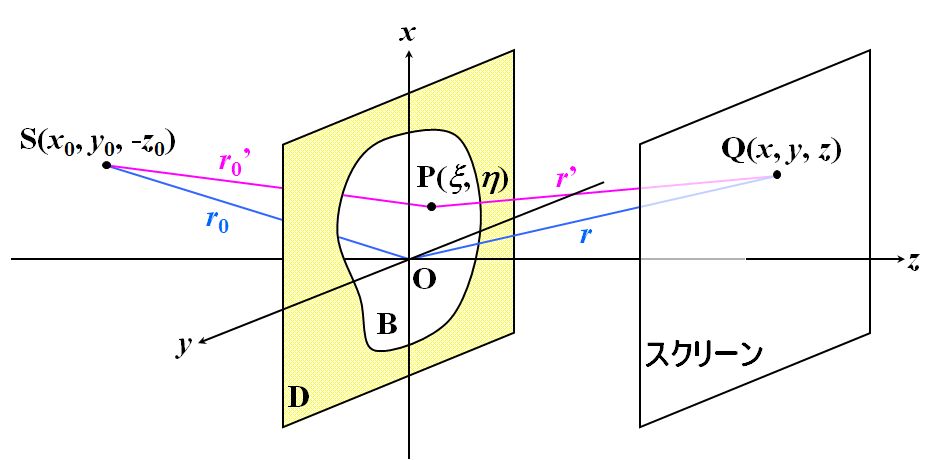 図4.2.1 回折の座標(1) 衝立Dに開いた孔Bの中心を原点とする直交座標系を定義し、光源Sは¥((x_0,y_0,-z_0)¥)、点Qは¥((x,y,z)¥)にあるとします。また、孔の内部にある1点をP¥((¥xi,¥eta,0)¥)と置きます。 |
|
 | はい。 | |
 |
ここで、孔の大きさは、光源S〜衝立Dの距離、衝立D〜点Qの距離のいずれに対しても小さい、という仮定を設けます。このとき、 近似①:¥(¥vec{¥mathstrut {¥rm SP}}¥)は¥(¥vec{¥mathstrut {¥rm SQ}}¥)と平行 近似②:¥(¥vec{¥mathstrut {¥rm PQ}}¥)は¥(¥vec{¥mathstrut {¥rm SQ}}¥)と平行 と考えてもよさそうですね?? |
|
 | なるほど。大胆な近似の意味が分かってきたかも。 | |
 |
また、 近似③:光源Sと点Pを結んだ線分の長さ¥({r_0}^{¥prime}¥)は、光源Sと原点Oを結んだ線分の長さ¥(r_0¥)と等しい 近似④:点Pと点Qを結んだ線分の長さ¥(r^{¥thinspace ¥prime}¥)は、原点Oと点Qを結んだ線分の長さ¥(r¥)と等しい と考えてもよさそうですね?? |
|
 |
そうすると、近似①と②から、 近似①':¥(¥vec{¥mathstrut n}¥)と¥(¥vec{¥mathstrut {r_0}^{¥prime}}¥)のなす角は、¥(¥vec{¥mathstrut n}¥)と¥(¥vec{¥mathstrut {¥rm SQ}}¥)のなす角に等しい 近似②':¥(¥vec{¥mathstrut n}¥)と¥(¥vec{¥mathstrut r^{¥thinspace ¥prime}}¥)のなす角は、¥(¥vec{¥mathstrut n}¥)と¥(¥vec{¥mathstrut {¥rm QS}}¥)のなす角に等しい わけですね。 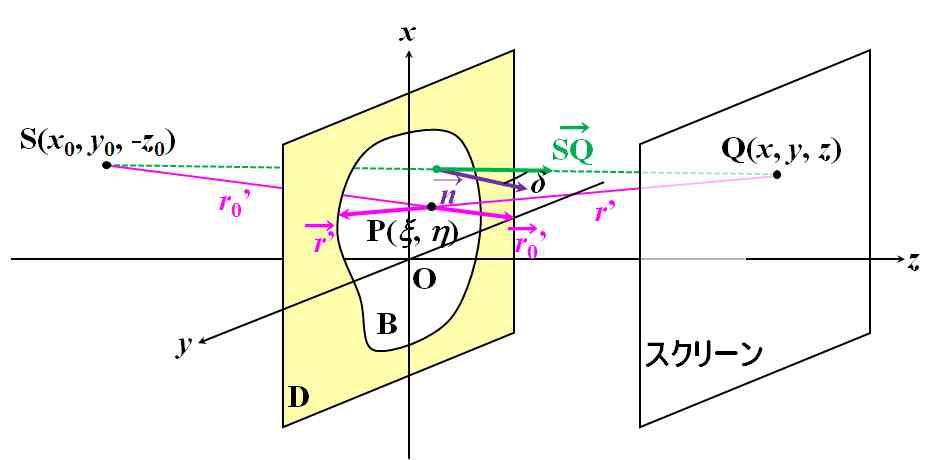 図4.2.2 回折の座標(2) |
|
 | ¥(¥vec{¥mathstrut n}¥)と¥(¥vec{¥mathstrut {¥rm SQ}}¥)のなす角を¥(¥delta¥)と置きましょう。そうすると、¥(¥vec{¥mathstrut n}¥)と¥(¥vec{¥mathstrut {¥rm QS}}¥)のなす角は、¥(¥pi-¥delta¥)になります。 | |
 | てことは、 ¥[ ¥cos ¥big( ¥vec{¥mathstrut n}, ¥vec{¥mathstrut r^{¥thinspace ¥prime}} ¥big) - ¥cos ¥big( ¥vec{¥mathstrut n}, {¥vec{¥mathstrut {r_0}^{¥prime}}} ¥big) ¥fallingdotseq ¥cos ¥left( ¥pi - ¥delta ¥right) - ¥cos ¥delta = -2 ¥cos ¥delta ¥tag{4.2.1} ¥] ですね。 | |
 | そうすると、式4.1.29は、 ¥[ U ¥left( {¥rm Q} ¥right) = - ¥frac{ik}{2 ¥pi } A ¥cos ¥delta ¥iint_{¥rm B} ¥frac{¥mathrm{e}^{ik ¥left( {r_0}^{¥prime} + r^{¥thinspace ¥prime} ¥right) }}{{r_0}^{¥prime}r^{¥thinspace ¥prime}} d ¥Gamma ¥fallingdotseq - ¥frac{iA}{¥lambda} ¥frac{¥cos ¥delta}{r_0 r} ¥iint_{¥rm B} ¥mathrm{e}^{ik ¥left( {r_0}^{¥prime} + r^{¥thinspace ¥prime} ¥right) } d ¥Gamma ¥tag{4.2.2} ¥] と書き直せます。 | |
 | ここで、近似③と④を適用かぁ。 | |
 | 次に、Pythagorasの定理から、 ¥[ ¥begin{align*} {r_0}^{¥prime} &= ¥sqrt{ ¥left( x_0 - ¥xi ¥right)^2 + ¥left( y_0 - ¥eta ¥right)^2 + {z_0}^2 } ¥¥ &= ¥sqrt{ {x_0}^2 + {y_0}^2 + {z_0}^2 - 2 ¥left(x_0 ¥xi + y_0 ¥eta ¥right) + ¥left( ¥xi^2 + ¥eta^2 ¥right) } ¥¥ &= ¥sqrt{ {r_0}^2 - 2 ¥left(x_0 ¥xi + y_0 ¥eta ¥right) + ¥left( ¥xi^2 + ¥eta^2 ¥right) } = r_0 ¥sqrt{ 1 - 2 ¥frac{x_0 ¥xi + y_0 ¥eta}{ {r_0}^2 } + ¥frac{ ¥xi^2 + ¥eta^2 }{ {r_0}^2 } } ¥¥ &¥approx r_0 ¥left[ 1 - ¥frac{x_0 ¥xi + y_0 ¥eta}{ {r_0}^2 } + ¥frac{ ¥xi^2 + ¥eta^2 }{ 2 {r_0}^2 } ¥right] = r_0 - ¥frac{x_0 ¥xi + y_0 ¥eta}{ r_0 } + ¥frac{ ¥xi^2 + ¥eta^2 }{ 2 r_0 } ¥tag{4.2.3} ¥end{align*} ¥] ¥[ ¥begin{align*} r^{¥thinspace ¥prime} &= ¥sqrt{ ¥left( x - ¥xi ¥right)^2 + ¥left( y - ¥eta ¥right)^2 + z^2 } ¥¥ &= ¥sqrt{ x^2 + y^2 + z^2 - 2 ¥left(x ¥xi + y ¥eta ¥right) + ¥left( ¥xi^2 + ¥eta^2 ¥right) } ¥¥ &= ¥sqrt{ r^2 - 2 ¥left(x ¥xi + y ¥eta ¥right) + ¥left( ¥xi^2 + ¥eta^2 ¥right) } = r ¥sqrt{ 1 - 2 ¥frac{x ¥xi + y ¥eta}{ r^2 } + ¥frac{ ¥xi^2 + ¥eta^2 }{ r^2 } } ¥¥ &¥approx r ¥left[ 1 - ¥frac{x ¥xi + y ¥eta}{ r^2 } + ¥frac{ ¥xi^2 + ¥eta^2 }{ 2 r^2 } ¥right] = r - ¥frac{x ¥xi + y ¥eta}{ r } + ¥frac{ ¥xi^2 + ¥eta^2 }{ 2 r } ¥tag{4.2.4} ¥end{align*} ¥] 途中、Taylor展開を使って近似しました。更に、 ¥[ ¥Delta ¥left( ¥xi, ¥eta ¥right) ¥equiv - ¥frac{x_0 ¥xi + y_0 ¥eta}{ r_0 } - ¥frac{x ¥xi + y ¥eta}{ r } + ¥frac{ ¥xi^2 + ¥eta^2 }{ 2 r_0 } + ¥frac{ ¥xi^2 + ¥eta^2 }{ 2 r } ¥tag{4.2.5} ¥] と定義すると―。 | |
 | 式4.2.2は、 ¥[ ¥begin{align*} U ¥left( {¥rm Q} ¥right) &= - ¥frac{iA}{¥lambda} ¥frac{¥cos ¥delta}{r_0 r} ¥iint_{¥rm B} ¥mathrm{e}^{ik ¥big[ r_0 + r + ¥Delta ¥left( ¥xi, ¥eta ¥right) ¥big] } d ¥Gamma ¥¥ &= - ¥frac{iA}{¥lambda} ¥frac{¥cos ¥delta}{r_0 r} ¥mathrm{e}^{ik ¥left( r_0 + r ¥right) } ¥iint_{¥rm B} ¥mathrm{e}^{ik ¥Delta ¥left( ¥xi, ¥eta ¥right) } d ¥Gamma ¥tag{4.2.6} ¥end{align*} ¥] になるってことですね。 | |
 | ¥(¥cfrac{x_0}{r_0}¥)と¥(¥cfrac{y_0}{r_0}¥)は¥(¥vec{¥mathstrut {¥rm OS}}¥)の方向余弦ですから、光線の進む向き¥(¥vec{¥mathstrut {¥rm SO}}¥)を考慮して、それぞれ¥((-l_0,-m_0)¥)としましょう。同様に、¥(¥cfrac{x}{r}¥)と¥(¥cfrac{y}{r}¥)は¥(¥vec{¥mathstrut {¥rm OQ}}¥)の方向余弦ですから、それぞれ¥((l,m)¥)とします。 | |
 | てことは、式4.2.5は、 ¥[ ¥begin{align*} ¥Delta ¥left( ¥xi, ¥eta ¥right) &= - ¥left( -l_0 ¥xi - m_0 ¥eta ¥right) - ¥left(l ¥xi + m ¥eta ¥right) + ¥frac{1}{2} ¥left( ¥frac{1}{r_0} + ¥frac{1}{r} ¥right) ¥left( ¥xi^2 + ¥eta^2 ¥right) ¥¥ &= - ¥left( l -l_0 ¥right) ¥xi - ¥left( m - m_0 ¥right) ¥eta + ¥frac{1}{2} ¥left( ¥frac{1}{r_0} + ¥frac{1}{r} ¥right) ¥left( ¥xi^2 + ¥eta^2 ¥right) ¥tag{4.2.7} ¥end{align*} ¥] ですね。 |
〜Fraunhofer回折〜
 | ここで、 ¥[ ¥frac{k}{2} ¥left( ¥frac{1}{r_0} + ¥frac{1}{r} ¥right) ¥left( ¥xi^2 + ¥eta^2 ¥right) ¥sim 0 ¥tag{4.2.8} ¥] だと、式4.2.7の第3項は式4.2.6の積分に寄与しないことは分かりますね?? | |
 | つまり、¥(¥xi^2+¥eta^2¥)が小さくて、¥(r_0¥)と¥(r¥)が大きい場合ですね。 | |
 | そうですが、それだとお互いのディメンジョンが揃ってないので、¥(¥cfrac{¥xi^2+¥eta^2}{¥lambda}¥)と比較するのがよいでしょう。 | |
 | なるほど。 | |
 |
式4.2.8のような近似が成立する回折をFraunhofer回折と言います。
 Joseph von Fraunhofer(1787〜1826) Fraunhoferは子供の頃、貧しかったために正規の教育を受けることができませんでした。 |
|
 | この人も、その手の境遇なんですね。 | |
 | 父親がレンズ職人だったので、その仕事を手伝って、レンズ磨きの腕を上げていくんですが、14歳のときに奉公先のガラス工場が倒壊して、そこに生き埋めになってしまいます。 | |
 | ひえ〜、それでどうなったんですか?? | |
 |
政治家のJoseph Utzschneiderによって救助されるんですが、この出会いがFraunhoferの運命を変えることになるのです。
 Joseph von Utzschneider(1763〜1840) |
|
 | 政治家とレンズ職人??あんまりピンと来ませんけど。 | |
 | Utzschneiderは、産業革命に成功したイギリスから光学ガラスを輸入していたことをずっと苦々しく思っていて、ドイツ本国で質のいいガラス製造工場を建設したい、ということを夢に描いていました。彼は、Fraunhoferの才能を見抜いて、1806年に創設した光学研究所に職人として雇うことにしたのです。 | |
 | なるほど〜。それにしても、凄い偶然ですね。 | |
 |
この研究所には、フリント・ガラス(鉛含有量の多い、高屈折率の硝材)の製造に成功したPierre-Louis Guinandという人がいて、その人の教えのもとで、レンズ製造技術に磨きをかけていくんですね。
 Pierre-Louis Guinand(1748〜1824) |
|
 | これも、人との出会いですね。 | |
 | そして、高精度の色消しレンズなどの開発に着手するわけですが、27歳のときに、その開発過程で重要な発見をします。輝線スペクトルの話、覚えていますか?? | |
 | e線とかd線とかいった、あれですね?? | |
 |
はい。この輝線スペクトルは、Fraunhoferが発見しました(論文)。Fraunhoferは、太陽光をプリズムを使って色分解したときに、暗線があるということに気が付いたのです。
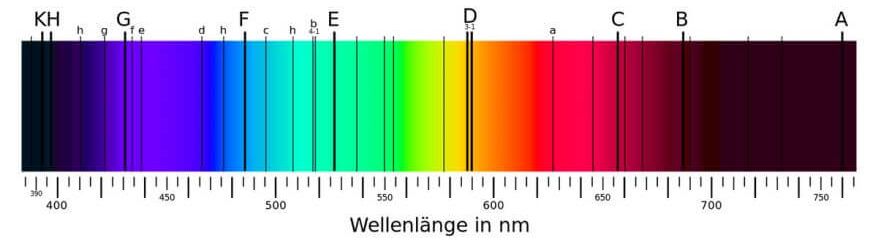 図4.2.3 Fraunhofer線 |
|
 | いっぱいありますね。 | |
 | これらをFraunhofer線と言いますが、Fraunhoferは系統的な研究を行い、570を超える暗線について波長を計測し、主要な線にAからKの記号を付け、弱い線については別の記号を付けました。 | |
 | そういうことなのか。前々から、何でd線とかe線って言うのか、不思議に思ってたんですよねぇ。 | |
 | どうしてこのような暗線が出現するのかというのは、後になってKirchhoffとBunsenによって解明されます。これもすでに説明したことですが、原子や分子はそれぞれ固有の振動とか回転をしていて、それと同じ振動数を持つ電磁波を強く吸収する、という話は覚えてますか?? | |
 | 分光計測のときのトピックスですね。 | |
 | 太陽からの光はいろいろな波長が混合しているわけですが、地表に届くまでの間にいろいろな原子、分子に出会い、そこで吸収されたものがスペクトルから抜けて暗線になる、というのがFraunhofer線が出現するメカニズムなのです。 | |
 | ということは、Fraunhofer線って、太陽の上層に存在する元素や、地球の大気の指紋スペクトルだってこと?? | |
 | そういうことです。 | |
 | へぇ。何か、いろんな話が繋がっていきますね〜。 | |
 | さて、Fraunhofer回折ですが、 ¥[ C_0 ¥equiv - ¥frac{iA}{¥lambda} ¥frac{¥cos ¥delta}{r_0 r} ¥mathrm{e}^{ik ¥left( r_0 + r ¥right) } ¥tag{4.2.9} ¥] とすると、式4.2.6は、 ¥[ U ¥left( {¥rm Q} ¥right) = C_0 ¥iint_{¥rm B} ¥mathrm{e}^{-ik ¥big[ ¥left( l -l_0 ¥right) ¥xi + ¥left( m - m_0 ¥right) ¥eta ¥big] } d ¥xi ¥eta ¥tag{4.2.10} ¥] となります。更に、 ¥[ ¥mu ¥equiv ¥frac{ l - l_0 }{¥lambda},¥quad ¥nu ¥equiv ¥frac{ m - m_0 }{¥lambda} ¥tag{4.2.11} ¥] と置けば、 ¥[ U ¥left( ¥mu, ¥nu ¥right) = C_0 ¥iint_{¥rm B} ¥mathrm{e}^{-2 ¥pi i ¥left( ¥mu ¥xi + ¥nu ¥eta ¥right) } d ¥xi d ¥eta ¥tag{4.2.12} ¥] です。式4.2.11の¥(¥mu¥)、¥(¥nu¥)は空間周波数と呼ばれます。 | |
 | 何か、ただ文字の置き換えをしているだけのような…。 | |
 | すぐに、ご利益が分かりますよ。ここで、¥(g¥left(¥xi,¥eta¥right)¥)という新しい関数を導入し、B内部のとき¥(1¥)、B外部のとき¥(0¥)と定義すると、式4.2.12は更に、 ¥[ U ¥left( ¥mu, ¥nu ¥right) = C_0 ¥int_{-¥infty}^{¥infty} ¥int_{-¥infty}^{¥infty} g ¥left( ¥xi, ¥eta ¥right) ¥mathrm{e}^{-2 ¥pi i ¥left( ¥mu ¥xi + ¥nu ¥eta ¥right) } d ¥xi d ¥eta ¥tag{4.2.13} ¥] と変形できます。さて問題です。式4.2.13を見て、何か思い当たることはありませんか?? | |
 | 思い当たること??う〜ん。何かゴチャゴチャしてきたなぁ、ってところですかね。 | |
 | …。そうではなくて、式4.2.13は¥(g¥left(¥xi,¥eta¥right)¥)の2次元Fourier変換になっているということですよ。 ¥[ U ¥left( ¥mu, ¥nu ¥right) = C_0 ¥mathcal{F} ¥big[ g ¥left( ¥xi, ¥eta ¥right) ¥big] ¥tag{4.2.14} ¥] | |
 | そう言われても、2次元Fourier変換を忘れているから、ピンと来ないで〜す。 | |
 | まぁ、いいです。とりあえず、式4.2.14のような形に変換できるというのがFraunhofer回折の特徴だと覚えてください。重要なことは、Fourier変換については計算手法が確立されているため、非常に短い時間で結果を求めることができる、という点です。 | |
 | そっか。FFTとか、ありますもんね。 | |
 | ¥(g¥left(¥xi,¥eta¥right)¥)は瞳関数と呼ばれますが、Fraunhofer回折の振幅分布は瞳関数の2次元Fourier変換に比例するわけです。 | |
 | 瞳関数は、この例だと開口の内部で一定値を取る矩形波型の関数でしたけど?? | |
 | ありがたいことに、任意の振幅と位相の分布を持つ複素関数に拡張しても差し支えありません。 | |
 | へぇ。つまり、¥(r_0¥)と¥(r¥)が¥(¥cfrac{¥xi^2+¥eta^2}{¥lambda}¥)に比べて充分に大きい場合はFraunhofer回折でスクリーンの回折パターンが取り扱えて、その結果は瞳関数の2次元Fourier変換で求まるってことですね。 | |
 | そういうことです。というわけで、次回は具体的な開口形状を想定して、回折パターンを求めてみましょう。 |
| 前頁へ | 戻る | 次頁へ |