 | Fraunhofer回折を矩形開口(\(2a\times 2b\))に適用し、回折パターンがどうなるか見てみましょう。ここで、入射する光は、開口に垂直な平行光束とします。 | |
 | ん??ということは、入射側の方向余弦は\((0,0,1)\)?? | |
 | はい。つまり、\(l_0=m_0=0\)です。よって、式4.2.11から、\(\mu=\cfrac{l}{\lambda}\)、\(\nu=\cfrac{m}{\lambda}\)となります。 | |
 | そうすると、式4.2.12は、 \[ \begin{align*} U \left( \mu, \nu \right) &= C_0 \int_{-a}^a \int_{-b}^b \mathrm{e}^{-2 \pi i \left( \mu \xi + \nu \eta \right) } d \xi d \eta = C_0 \int_{-a}^a \mathrm{e}^{ -2 \pi i \mu \xi } d \xi \int_{-b}^b \mathrm{e}^{ -2 \pi i \nu \eta } d \eta \\ &= C_0 \left[ \frac{ \mathrm{e}^{ -2 \pi i \mu \xi } }{ -2 \pi i \mu } \right]_{-a}^a \left[ \frac{ \mathrm{e}^{ -2 \pi i \nu \eta } }{ -2 \pi i \nu } \right]_{-b}^b = C_0 \frac{ 2 \sin{ 2 \pi \mu a } }{ 2 \pi \mu } \frac{ 2 \sin{ 2 \pi \nu b } }{ 2 \pi \nu } \\ &= 4C_0ab \frac{ \sin{ 2 \pi \mu a } }{ 2 \pi \mu a } \frac{ \sin{ 2 \pi \nu b } }{ 2 \pi \nu b } = 4C_0ab {\rm sinc} \left( 2 \pi \mu a \right) {\rm sinc} \left( 2 \pi \nu b \right) \\ &= 4C_0ab {\rm sinc} \left( \frac{2 \pi a}{\lambda} l \right) {\rm sinc} \left( \frac{2 \pi b}{\lambda} m \right) \tag{4.2.15} \end{align*} \] になりますね。 | |
 |
強度分布\(I\)は、\(U^2\)なので、定数部分を\(I_0\)とすれば、
\[
I = I_0 {\rm sinc}^2 \left( \frac{2 \pi a}{\lambda} l \right) {\rm sinc}^2 \left( \frac{2 \pi b}{\lambda} m \right) \tag{4.2.16}
\]
です。\(I_0\)は\(l=m=0\)(つまり、\(x=y=0\))のときに実現するので、中心強度と言ってもいいでしょう。これを図示したのが図4.2.4です。
 図4.2.4 矩形開口でのFraunhofer回折 |
|
 | 直感的にも納得な回折パターンですね。 | |
 | ここで、\(x\)軸に沿った強度分布に着目(\(\nu=0\))すると、式4.2.16は、 \[ I\left(\mu\right) = I_0 {\rm sinc}^2 \left( \frac{2 \pi a}{\lambda} l \right) =I_0 \left(\frac{\sin 2\pi\mu a}{2\pi\mu a} \right)^2 \tag{4.2.17} \] となります。この回折像の強度が極大、極小となる位置を求めてみましょう。 | |
 | それは、式4.2.17を微分して、 \[ \begin{align*} \frac{\partial I}{\partial \mu} &= 2 I_0 \frac{\sin 2\pi\mu a}{2\pi\mu a} \left[\frac{\cos 2\pi\mu a}{\mu}-\frac{\sin 2\pi\mu a}{2\pi\mu^2 a}\right] \\ &= 2 I_0 \frac{\sin 2\pi\mu a}{\left(2\pi a \right)^2 \mu^3} \left( 2\pi\mu a \cos 2\pi\mu a - \sin 2\pi\mu a \right) = 0 \end{align*} \] を解けばいいのでは?? | |
 | はい。まず、極小(\(I=0\))の位置は、整数を\(N\)としたとき、 \[ \sin 2\pi\mu_N a = 0 \quad \Leftrightarrow \quad 2\pi\mu_N a = N \pi \quad \Leftrightarrow \quad \mu_N = \frac{N}{2a} \tag{4.2.18} \] と分かります。つまり、暗線の間隔は等間隔(\(\Delta \mu = \cfrac{1}{2a}\))です。 | |
 | 極大の位置は、整数を\(M\)としたとき、 \[ 2\pi\mu_M a \cos 2\pi\mu_M a - \sin 2\pi\mu_M a = 0 \tag{4.2.19} \] ですね。でも、これ以上、解けないのでは?? | |
 |
解けません。が、式4.2.19は、\(2\pi\mu_N a = s\)と置くと、
\[
s \cos s - \sin s = 0 \quad \Leftrightarrow \quad s \cos s = \sin s \quad \Leftrightarrow \quad s = \tan s
\]
なので、
\[
\left\{ \
\begin{array}{l}
t = \tan s \\
t = s
\end{array}
\right.
\]
の交点を求めることと同じですし、それをグラフにすると図4.2.5のようになることから、\(M\)が大きくなると等間隔に近づいていくだろう、ということは直感的に理解できます。
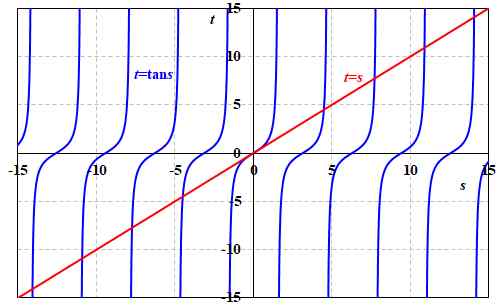 図4.2.5 式4.2.19の解 |
|
 | なるほど。 | |
 | 波長が一定である場合、暗線に着目すると、その間隔\(\Delta \mu\)は\(a\)に(\(\Delta \nu\)は\(b\)に)反比例するわけですから、\(b\)をグイッと広げて、\(a\)をぎゅっと縮めると、図4.2.4は縦方向に潰れて、横方向に引き伸ばされたパターンになることが分かります。 | |
 | いわゆる、スリットの回折ですね。 | |
〜円形開口でのFraunhofer回折〜
 | 次は、Fraunhofer回折を円形開口(半径\(\rho_0\))に適用し、回折パターンがどうなるか見てみましょう。 | |
 | 入射する光は平行光束ですか?? | |
 | そうですね。 | |
 | やっぱり、極座標系で考えた方がよさそうですよね。 | |
 | 回折パターンも同心円状になることが予想されますからね。その方が都合がよさそうです。 | |
 | だったら、開口の方は、 \[ \left\{ \ \begin{array}{l} \xi = \rho \cos \theta \\ \eta = \rho \sin \theta \end{array} \right. \tag{4.2.20} \] スクリーンの方は、 \[ \left\{ \ \begin{array}{l} \mu = w \cos \phi \\ \nu = w \sin \phi \end{array} \right. \tag{4.2.21} \] って置きたくなりますね。 | |
 | いいと思います。 | |
 | そうすると、 \[ \begin{align*} \mu \xi + \nu \eta &= w \cos \phi \cdot \rho \cos \theta + w \sin \phi \cdot \rho \sin \theta \\ &= \rho w \left( \cos \phi \cos \theta + \sin \phi \sin \theta \right) = \rho w \cos \left( \phi - \theta \right) \tag{4.2.22} \end{align*} \] \[ \begin{align*} d \xi d \eta &= \left| \begin{array}{cc} \cfrac{\partial \xi}{\partial \rho} & \cfrac{\partial \xi}{\partial \theta} \\ \cfrac{\partial \eta}{\partial \rho} & \cfrac{\partial \eta}{\partial \theta} \end{array} \right| d \rho d \theta = \left| \begin{array}{cc} \cos \theta & - \rho \sin \theta \\ \sin \theta & \rho \cos \theta \end{array} \right| d \rho d \theta \\ &= \left( \rho \cos^2 \theta + \rho \sin^2 \theta \right) d \rho d \theta = \rho \left( \cos^2 \theta + \sin^2 \theta \right) d \rho d \theta = \rho d \rho d \theta \tag{4.2.23} \end{align*} \] だから、式4.2.12は、 \[ U \left( w, \phi \right) = C_0 \int_{0}^{\rho_0} \int_{0}^{2 \pi} \mathrm{e}^{-2 \pi i \rho w \cos \left( \phi - \theta \right) } \rho d \rho d \theta \tag{4.2.24} \] になりますね。 | |
 | 結果は回転対称であることが明らかなので、\(\phi\)の成分については、適当な1つの値について計算しておけば充分です。というわけで、\(\phi=0\)としておきましょう。 \[ U \left( w \right) = C_0 \int_{0}^{\rho_0} \int_{0}^{2 \pi} \mathrm{e}^{2 \pi i \rho w \cos \theta } \rho d \rho d \theta \tag{4.2.25} \] | |
 | でも、これで手詰まりですよ。 | |
 | そうではないですね。Bessel関数を導入することで、もう少し計算を進めることができます。 \[ J_n \left( x \right) = \frac{i^{-n}}{2 \pi} \int_{0}^{2 \pi} \mathrm{e}^{i \left( x \cos \theta + n \theta \right) } d \theta \tag{4.2.26} \] | |
 | お〜、何か凄い関数が登場しましたね。 | |
 | 特殊関数の1つですが、Bessel関数は充分研究されているので、安心して使って大丈夫です。 | |
 | う〜ん、そうすると、式4.1.26で\(n=0\)、\(x=2\pi\rho w\)って置くと、式4.1.25に似た感じになりますね。 \[ J_0 \left( 2 \pi \rho w \right) = \frac{1}{2 \pi} \int_{0}^{2 \pi} \mathrm{e}^{2 \pi i \rho w \cos \theta } d \theta \tag{4.2.27} \] | |
 | つまり?? | |
 | つまり―。 \[ U \left( w \right) = C_0 \int_{0}^{\rho_0} 2 \pi J_0 \left( 2 \pi \rho w \right) \rho d \rho \tag{4.2.28} \] かな。さすがに、これ以上は―。 | |
 | 計算できますね。 | |
 | え?? | |
 | もう1つ、Bessel関数についての公式を使います。 \[ \frac{d}{dx} \Big[ x^n J_n \left( x \right) \Big] = x^n J_{n-1} \left( x \right) \tag{4.2.29} \] | |
 | 何と!! | |
 | だから、充分研究されていると言ったでしょう?? | |
 | そうすると、式4.1.29で\(n=1\)、\(x=2\pi\rho w\)って置くと、式4.1.28に似た感じになるか…。 \[ \begin{align*} {\rm l.h.s.} &= \frac{d}{dx} \Big[ x J_1 \left( x \right) \Big] = \frac{d}{d \rho} \frac{d \rho}{dx} \Big[ x J_1 \left( x \right) \Big] = \frac{d}{d \rho} \frac{1}{2 \pi w} \Big[ 2 \pi \rho w J_1 \left( 2 \pi \rho w \right) \Big] \\ &= \frac{d}{d \rho} \Big[ \rho J_1 \left( 2 \pi \rho w \right) \Big] \end{align*} \] \[ {\rm r.h.s.} = x J_0 \left( x \right) = 2 \pi \rho w J_0 \left( 2 \pi \rho w \right) \] | |
 | つまり、 \[ \begin{align*} \frac{d}{d \rho} \Big[ \rho J_1 \left( 2 \pi \rho w \right) \Big] &= 2 \pi \rho w J_0 \left( 2 \pi \rho w \right) \\ &\Leftrightarrow \quad d \left[ \frac{\rho}{w} J_1 \left( 2 \pi \rho w \right) \right] = 2 \pi J_0 \left( 2 \pi \rho w \right) \rho d \rho \tag{4.2.30} \end{align*} \] ですから、式4.2.28は、 \[ U \left( w \right) = C_0 \left[ \frac{\rho}{w} J_1 \left( 2 \pi \rho w \right) \right]_{0}^{\rho_0} = C_0 \frac{\rho_0}{w} J_1 \left( 2 \pi \rho_0 w \right) = C_0 \pi {\rho_0}^2 \frac{2 J_1 \left( 2 \pi \rho_0 w \right)}{ 2 \pi \rho_0 w} \tag{4.2.31} \] となるのです。 | |
 | 強度分布\(I\)は、定数部分を\(I_0\)とすれば、 \[ I = I_0 \left( \frac{2 J_1 \left( 2 \pi \rho_0 w \right)}{ 2 \pi \rho_0 w} \right)^2 \tag{4.2.32} \] ってことか。 | |
 |
これを図示したのが、図4.2.6です。
 図4.2.6 円形開口でのFraunhofer回折 | |
 | 予想どおりの回折パターンですね。 |
〜光学機器の分解能〜
 |
中心の円盤が最も明るく見えますが、この部分をAiryディスクと言います。Airyは天文学者ですが、天体望遠鏡の研究から、この円盤が見出されました(論文)。
 Sir George Biddell Airy(1801〜1892) |
|
 | この円盤の半径\(w_1\)って、 \[ J_1 \left( 2 \pi \rho_0 w_1 \right) = 0 \tag{4.2.33} \] を求めれば出せると思うけど、計算できるんですか?? | |
 | それはBessel関数の零点問題になりますが、Airyディスクに相当するのは第1零点なので、約3.8317ということが分かっています。 | |
 | つまり、 \[ 2 \pi \rho_0 w_1 = 3.8317 \quad \Leftrightarrow \quad \rho_0 w_1 \fallingdotseq 0.61 \tag{4.1.34} \] ってこと?? | |
 |
そういうことになりますね。しかし、Airyディスクは、このままではあまり有難味が分かりません。そこで、先ほど\(\phi=0\)で議論すれば充分だと話したので式4.2.21から\(w=\mu\)、平行光束であることを前提としたので\(\mu=\cfrac{l}{\lambda}\)であることを思い出しましょう。そうすると、式4.2.34は、
\[
\rho_0 w_1 = \rho_0 \mu_1 = \rho_0 \frac{l_1}{\lambda} = 0.61 \quad \Leftrightarrow \quad l_1= 0.61 \frac{\lambda}{\rho_0} \tag{4.2.35}
\]
となります。そして、この関係をレンズの集光にあてはめてみるわけです。
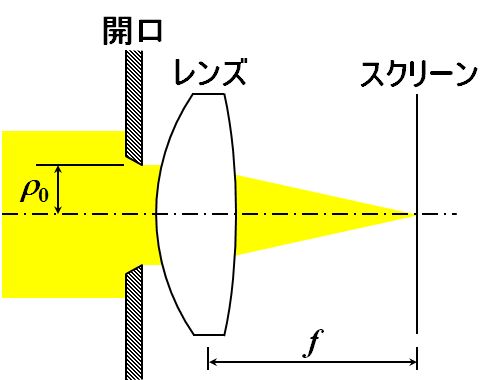 図4.2.7 レンズで集光したときの回折の影響 |
|
 | 開口の直後にレンズを設置するわけですね。 | |
 | このとき、レンズの焦点距離を\(f\)とすれば、\(l_1=\cfrac{w_1}{f}\)ですから―。 | |
 | 式4.2.35は、 \[ \frac{w_1}{f}= 0.61 \frac{\lambda}{\rho_0} \quad \Leftrightarrow \quad w_1= 0.61 \lambda \frac{f}{\rho_0} \tag{4.2.36} \] ですね。 | |
 | この結果から重要なことがいくつか導けます。1つ目は、レンズに入射した光束は、幾何光学的には1点に集光されるが、波動光学的には回折の影響により式4.2.36によって決まる半径\(w_1\)のスポット以下に集光させることはできないということです。 | |
 | お〜。ガリガリ計算しただけだと思ったら、そんな結論に向かっていただなんて!! | |
 | これは、次のように考えると理解しやすいでしょう。開口を通過した平行光束は、回折の影響により外側へ広がろうという動きがかかります。一方、レンズの作用により、内側に集光しようという動きもかかります。しかし、どれだけ優れたレンズを持ってきても、光が外側へ広がろうという作用を止めることはできない。従って、幾何光学のように、1点に光を集めることはできず、ある広がりを持ってしまう、それがAiryディスクの意味だ、ということです。 | |
 | 回折作用のささやかな抵抗って感じか。 | |
 | 2つ目は、半径\(w_1\)のスポットの内部にある2つの点を分離して観察することはできないということです。つまり、Airyディスクというのはレンズの分解能を決定する指標になる、ということでもあるのです。 | |
 | あ〜、だから天体望遠鏡の研究が絡んでくるんですね。 | |
 |
これを研究者の名(論文)をとって、Rayleighの解像限界と言ったりもしますね。
 3rd Baron Rayleigh(1842〜1919) |
|
 |
Rayliegh??シルバーズ・レイリー??
 シルバーズ・レイリー |
|
 | それはワン・ピース。Raylieghはイギリスの物理学者です。この人は大変に勉強好きで、そのわりに子供の頃は病気がちだったので正規の教育を受けることができませんでした。 | |
 | この人も、イギリス特有の変わった経歴の持ち主ってことか…。 | |
 |
ですから、その反動が成人してから爆発します。1873年に男爵の爵位を授かるんですが、莫大な敷地の管理は弟に委ねて、研究に没頭するのです。それで散乱理論を完成させ、Ramsayと共同研究して新元素であるアルゴンを発見(論文)し、ノーベル賞を受賞します。
 William Ramsay(1852〜1916) その後、黒体放射の現象を古典理論で厳密に議論して、有名なRayleigh-Jeansの法則(論文)を導きます。  Sir James Hopwood Jeans(1877〜1946) |
|
 | それって、Planckの光量子化説に繋がるやつですよね?? | |
 |
そうです。Planckは、Rayleigh-Jeansの法則とWienの放射法則(論文)の間にある矛盾を解消するために、光量子化説の概念に到達します。この辺の話は、Kirchhoffも重要な関わりをしていて、なかなか面白いんですが、脱線がすぎるのでやめておきましょう。
 Wilhelm Carl Werner Otto Fritz Franz Wien(1864〜1928) |
|
 | な〜んだ。 | |
 | ただ、Raylieghは、これだけの業績を上げているものの、古典物理学の枠から逃れることのできなかった人で、量子論や相対論を一切認めることなく生涯を閉じてしまいます。 | |
 | 頭がよくても限界があるってことかぁ。 | |
 | 話を元に戻しましょう。3つ目は、開口が円形の場合、集光された回折パターンは、Airyディスク以外にも小さなピークを持つたくさんの同心円の集合体になるということです。この小さなピークをside-lobeと言ったりもしますね。 | |
 | side-lobeの極大値って、どのくらいなんですか?? | |
 | Airyディスクのピーク強度を1に正規化した場合、2番目の輪帯の極大値は1.75%程度です。 | |
 | そんなに小さいんだ。じゃ、あまり気にする必要はなさそうですね。 | |
 | 4つ目は、レンズを通して集光したスポットは、波長と焦点距離に比例し、開口の大きさに反比例するということです。 | |
 | ん??ん??ちょっと待って。開口が大きくなればなるほど、スポットは小さくなっていくってこと?? | |
 | そうです。 | |
 | え〜、何か不思議〜。 | |
 | 確かに直感と反する結論ですからね。そう思われても仕方がないです。しかし、この関係はMFPの検討では比較的よく利用されますね。 | |
 | 例えば?? | |
 | よく話題になるのは、短波長レーザの採用検討です。 | |
 | あ〜、波長が短くなればスポットが絞れるから。でも、一般的には赤色が使われてますよね?? | |
 | 短波長レーザであれば高精細な画像が狙えるという話は、理屈上は間違いないのですが、赤色から青色に変えれば、それに対応した感光体を開発しないといけません。また、光学系の硝材の種類の問題もありますね。 | |
 | ということは、実例はない?? | |
 | そんなことはないですよ。多くはありませんが、実例はあります(論文)。あと、事業部が新商品を立ち上げる場合に、従来機を使ってビーム・スポットだけ変えて画像実験をやりたい、というケースがあります。こういうとき、どうすればビーム・スポットを絞れるか、とよく問い合わせが来るんですが、一番手っ取り早いのは、アパーチャーを広げなさい、という解決方法です。 | |
 | 開口(アパーチャー)を広げるとスポットが絞れるからですね。ん〜、でも、それなら実験に使っている従来機は、何でアパーチャーを広げなかったんだろう??小径ビーム・スポットが必要なかったから?? | |
 | 違います。アパーチャーだけでビーム・スポット・サイズをコントロールできるなら、レンズ設計なんてそもそも不要でしょ?? | |
 | あ、そっか。 | |
 | つまり、感光体上のビーム・スポット・サイズと言った場合、A3サイズならA3サイズすべての場所で同じビーム・スポット・サイズであることが求められるわけです。だから、従来機で単にアパーチャーを広げると、部分的にはビーム・スポット・サイズが絞れても、それはすべての場所で達成できることを意味しません。 | |
 | だったら、画質評価にならないのでは?? | |
 | 基礎的な評価をするのにA3サイズのすべての領域は必要ないのです。部分的にビーム・スポット・サイズが絞られるのであれば、そこのエリアだけで統計処理することで充分有益な議論ができるんですよ。 | |
 | そうすると、事業部に情報を提供するときは、アパーチャーの寸法だけではなくて、ビーム・スポット・サイズが絞られる範囲を明確にする必要があるってことですね。 | |
 | そうです。ステーク・ホルダーが多い場合は、後で誤解が発生しないように、そういうコミュケーションがとても大切になります。 |
| 前頁へ | 戻る | 次頁へ |