 | Fresnel回折は式4.2.8が無視できません。このとき、近似③、④では誤差が大きくなってくる懸念が発生します。そこで新たな近似を導入します。 | |
 | 仕切り直しか…。 | |
 |
新たに設定される近似は、 近似⑤:光源Sと点Pを結んだ線分の長さ\({r_0}^{\prime}\)は、光源Sと点Pmを結んだ線分の長さ\(R_0\)と等しい 近似⑥:点Pと点Qを結んだ線分の長さ\(r^{\thinspace \prime}\)は、点Pmと点Qを結んだ線分の長さ\(R\)と等しい です。Pmは線分SQと衝立Dの交点\(\left(\xi_m,\eta_m, 0\right)\)です。 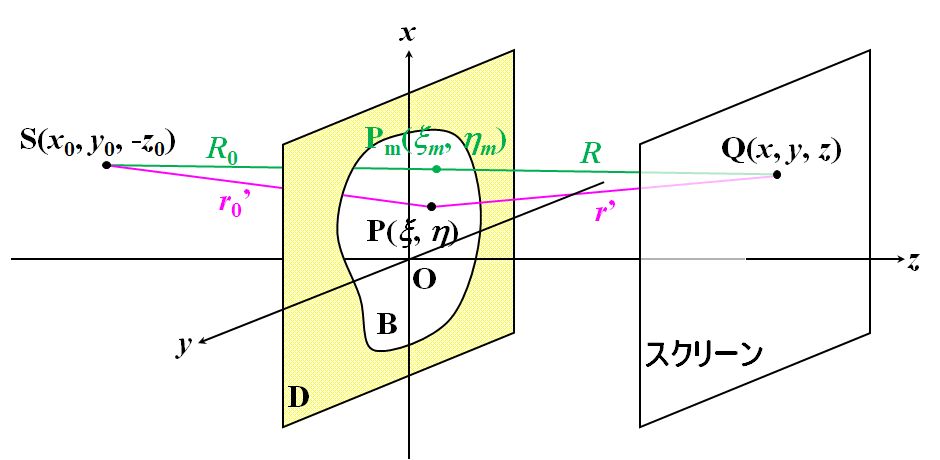 図4.3.1 回折の座標(3) |
|
 | 原点Oの代わりに点Pmを持ってきたわけですね。 | |
 | そうすると、式4.2.2は、 \[ U \left( {\rm Q} \right) = - \frac{ik}{2 \pi } A \cos \delta \iint_{\rm B} \frac{\mathrm{e}^{ik \left( {r_0}^{\prime} + r^{\thinspace \prime} \right) }}{{r_0}^{\prime} r^{\thinspace \prime}} d \Gamma \fallingdotseq - \frac{iA}{\lambda} \frac{\cos \delta}{R_0 R} \iint_{\rm B} \mathrm{e}^{ik \left( {r_0}^{\prime} + r^{\thinspace \prime} \right) } d \Gamma \tag{4.3.1} \] と書き直せます。 | |
 | このまま計算を進めたら、Fraunhofer回折のときと何も変わらないのでは?? | |
 | ですので、Pythagorasの定理を計算する際に、ひと工夫するのです。 \[ \begin{align*} {r_0}^{\prime} &= \sqrt{ \left( x_0 - \xi \right)^2 + \left( y_0 - \eta \right)^2 + {z_0}^2 } = z_0 \sqrt{ 1 + \frac{\left( x_0 - \xi \right)^2}{{z_0}^2} + \frac{\left( y_0 - \eta \right)^2}{{z_0}^2} } \\ &\approx z_0 \left[ 1 + \frac{\left( x_0 - \xi \right)^2}{2 {z_0}^2} + \frac{\left( y_0 - \eta \right)^2}{2 {z_0}^2} \right] = z_0 + \frac{\left( x_0 - \xi \right)^2}{2 z_0} + \frac{\left( y_0 - \eta \right)^2}{2 z_0} \tag{4.3.2} \end{align*} \] \[ \begin{align*} r^{\thinspace \prime} &= \sqrt{ \left( x - \xi \right)^2 + \left( y - \eta \right)^2 + z^2 } = z \sqrt{ 1 + \frac{\left( x - \xi \right)^2}{z^2} + \frac{\left( y - \eta \right)^2 }{z^2} } \\ &\approx z \left[ 1 + \frac{\left( x - \xi \right)^2}{2 z^2} + \frac{\left( y - \eta \right)^2 }{2 z^2} \right] = z + \frac{\left( x - \xi \right)^2}{2 z} + \frac{\left( y - \eta \right)^2 }{2 z} \tag{4.3.3} \end{align*} \] よって、途中計算を省くと、 \[ \begin{align*} {r_0}^{\prime} + r^{\thinspace \prime} &= z_0 + z + \frac{\left( x_0 - x \right)^2 + \left( y_0 - y \right)^2}{2 \left( z_0 + z \right)} \\ & \quad \quad \quad + \frac{\left( \xi - \xi_m \right)^2 + \left( \eta - \eta_m \right)^2}{2} \left( \frac{1}{z_0} + \frac{1}{z} \right) \tag{4.3.4} \end{align*} \] となります。 | |
 | \(r_0\)と\(r\)が使えないから、\(z_0\)と\(z\)に注目してTaylor展開ってことか。 | |
 | 更に、 \[ \begin{align*} R_0 + R &= \sqrt{ \left( x_0 - x \right)^2 + \left( y_0 - y \right)^2 + \left( z_0 + z \right)^2 } \\ &= \left( z_0 + z \right) \sqrt{ 1 + \frac{\left( x_0 - x \right)^2 + \left( y_0 - y \right)^2}{\left( z_0 + z \right)^2} } \\ &\approx \left( z_0 + z \right) \left[ 1 + \frac{\left( x_0 - x \right)^2 + \left( y_0 - y \right)^2}{2 \left( z_0 + z \right)^2} \right] \\ &= z_0 + z + \frac{\left( x_0 - x \right)^2 + \left( y_0 - y \right)^2}{2 \left( z_0 + z \right)} \tag{4.3.5} \end{align*} \] ですから、式4.3.4は、 \[ {r_0}^{\prime} + r^{\thinspace \prime} = R_0 + R + \frac{\left( \xi - \xi_m \right)^2 + \left( \eta - \eta_m \right)^2}{2} \left( \frac{1}{z_0} + \frac{1}{z} \right) \tag{4.3.6} \] となります。 | |
 | てことは、式4.3.1は、 \[ \begin{align*} U \left( {\rm Q} \right) &= - \frac{iA}{\lambda} \frac{\cos \delta}{R_0 R} \mathrm{e}^{ik \left( R_0 + R \right) } \\ & \quad \quad \quad \iint_{\rm B} \exp \left[ ik \frac{\left( \xi - \xi_m \right)^2 + \left( \eta - \eta_m \right)^2}{2} \left( \frac{1}{z_0} + \frac{1}{z} \right) \right] d \xi d \eta \tag{4.3.7} \end{align*} \] になるってことですね。 | |
 | しかし、Fraunhofer回折で議論したように、ここから先、式4.3.7を矩形開口だとか円形開口だとかに適用させようとすると、計算はかなり大変です。 | |
 | そうなんだ。 | |
 | 例えば、矩形開口に適用すると、その回折パターンを解析するにはFresnel積分という超越関数を取り扱わないといけないですし、円形開口に適用すると、Lommel関数の知識も必要になります。 | |
 | 聞いたこともない関数だ。 | |
 | ですから、Fresnel回折については、これ以上の深入りはやめておきましょう。 | |
 | お、やったね!! | |
 | 重要なのは、開口とスクリーンの距離に着目したときに、その距離がうんと離れていればFraunhofer回折で処理できる、近い場合はFresnel回折で処理しないといけない、ということです。そして、Fraunhofer回折は瞳関数の2次元Fourier変換で計算できるけど、Fresnel回折は実直に積分計算しないとどうにもならない、ということです。 | |
 | 光源とスクリーンの距離は関係ない?? | |
 | いえ。関係なくはないですが、多くの光学系は開口に平行光束を入射させますからね。\(z_0=\infty\)と考えることができるので、スクリーン側だけケアしておけば充分です。 | |
 | Fresnel回折で計算すると、どのくらい時間がかかるんですか?? | |
 | スクリーン上の1点の強度を計算するのに、開口の面積分が必要です。それをスクリーン上のすべての点で実行するから、ざっとFraunhofer回折を計算する4倍の時間が必要ですね。 | |
 | それって、結構な負担ですね。 | |
 | 今は計算機のパワーが格段に向上しているので、Fresnel回折で計算するのもあんまり負担ではないでしょうけど、少し前までは、どっちで計算するかは業務効率の観点から非常に重要な問題でした。 |
~どちらの回折で議論すべきか~
 | そうすると、その見極めが大切ですよね。 | |
 |
そのとおりです。では、LSUを例に、その辺の問題を考えてみましょう。
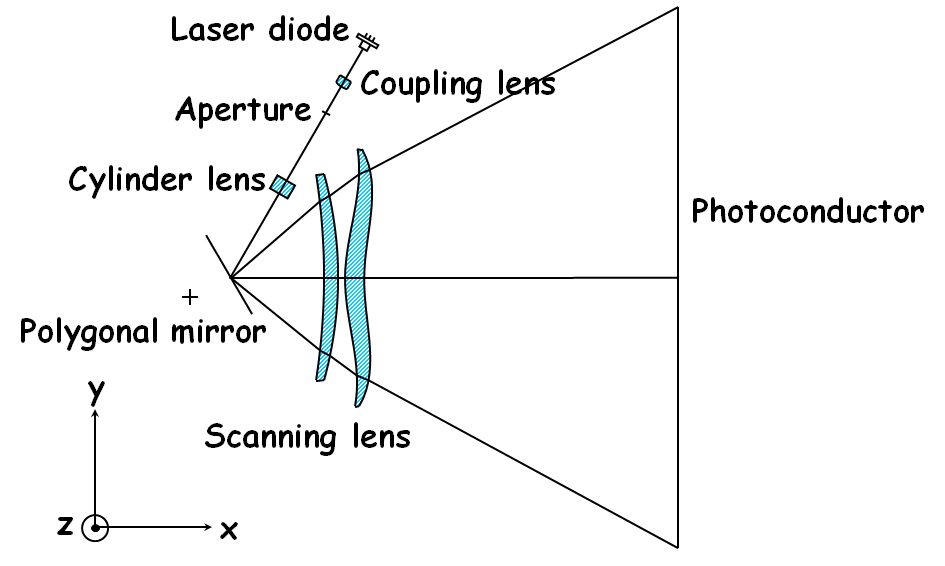 図4.3.2 走査光学系 |
|
 | 図4.3.2のようなLSUでビーム・スポット・サイズを計算する場合、どっちの回折で計算すべきか、ってことか。そうすると、アパーチャー~感光体までの距離を測って―。ん~、でも、Fraunhofer回折とFresnel回折の境界線が分からないですよ。 | |
 | その前に、アパーチャー~感光体までの距離を測る、というのが、すでにNGです。 | |
 | え~。だって、開口とスクリーンの距離に着目するって言いましたよ?? | |
 | ですが、図4.3.2はレンズがいっぱい入ってますからね。今までのような単純な議論は成立しません。 | |
 | ムムム。確かに。そうすると、何か工夫が必要ですね。 | |
 | そこで思い出してほしいのは、光学系には「像」という考え方があるということです。つまり、アパーチャーの回折情報は、光学系の作用によって作られたアパーチャーの像の位置にワープしたと考えればよいわけです。 | |
 | そっか!!アパーチャーの像と感光体までの距離に注目すればいいってことか。 | |
 |
図4.3.3は、図4.3.2の走査光学系をより簡単に模式化したものです。
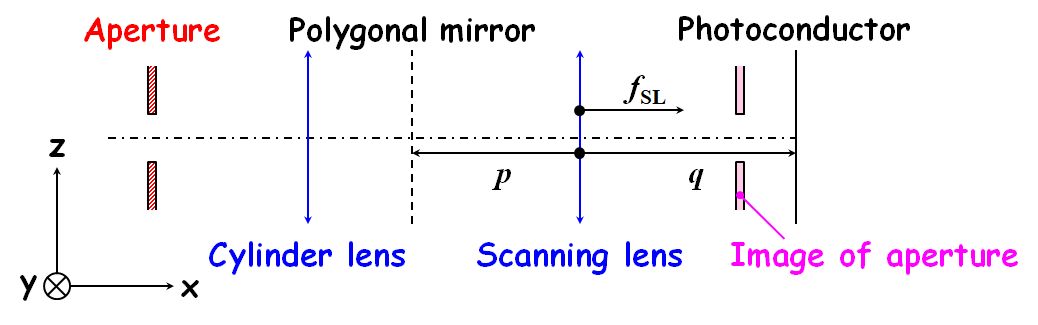 図4.3.3 走査光学系(ポリゴン・ミラーの回転軸に平行な平面) |
|
 | そうすると、シリンダー・レンズと走査レンズの作用でアパーチャーの像ができるから、その像の位置を求めたくなりますね。 | |
 | まず、図4.3.3において、走査レンズの作用により、ポリゴン・ミラーと感光体が共役の関係になっているので、ポリゴン・ミラー~走査レンズの主点の距離を\(p\)、走査レンズの主点~感光体の距離を\(q\)、走査レンズの焦点距離を\(f_{\rm SL}\)とすると、 \[ \frac{1}{q} = \frac{1}{f_{\rm SL}} + \frac{1}{p} \tag{4.3.8} \] となります。一方、この走査レンズの倍率\(\beta\)は、 \[ \beta = \frac{q}{p} \tag{4.3.9} \] です。よって、 \[ \frac{1}{p \beta} = \frac{1}{f_{\rm SL}} + \frac{1}{p} \quad \Leftrightarrow \quad \frac{1}{p} \left( \frac{1}{\beta} - 1 \right) = \frac{1}{f_{\rm SL}} \quad \Leftrightarrow \quad p = f_{\rm SL} \frac{1 - \beta}{\beta} \tag{4.3.10} \] となります。 | |
 | \(q\)は、 \[ q = p \beta = f_{\rm SL} \left( 1 - \beta \right) \tag{4.3.11} \] ですね。 | |
 |
次に、アパーチャーの像について考えてみましょう。
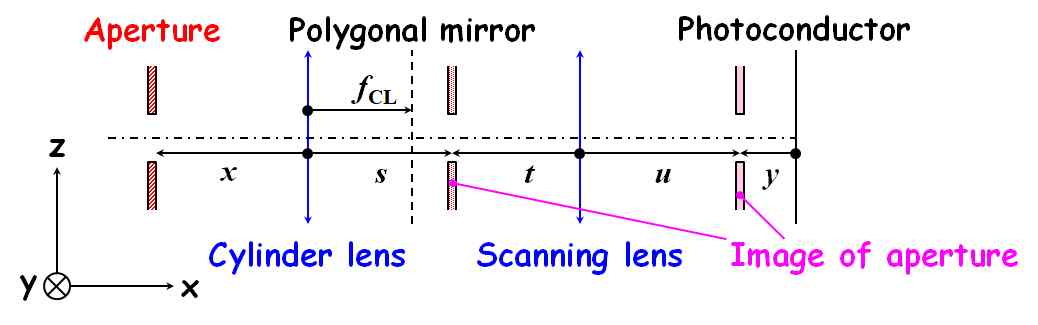 図4.3.4 アパーチャーの像の追跡(ポリゴン・ミラーの回転軸に平行な平面) |
|
 | 図4.3.4を見ると、アパーチャーはシリンダー・レンズの作用でいったん結像して、それがまた走査レンズの作用で感光体の近くに結像しているように見えますね。 | |
 | そのとおりです。なので、アパーチャー~シリンダー・レンズの主点の距離を\(x\)、シリンダー・レンズの主点~アパーチャーの像(第1)の距離を\(s\)、シリンダー・レンズの焦点距離を\(f_{\rm CL}\)とすると、 \[ \frac{1}{s} = \frac{1}{f_{\rm CL}} + \frac{1}{x} = \frac{x + f_{\rm CL}}{x f_{\rm CL}} \quad \Leftrightarrow \quad s = \frac{x f_{\rm CL}}{x + f_{\rm CL}} \tag{4.3.12} \] となります。また、アパーチャーの像(第1)~走査レンズの主点の距離を\(t\)、走査レンズの主点~アパーチャーの像(第2)の距離を\(u\)とすると、 \[ \frac{1}{u} = \frac{1}{f_{\rm SL}} + \frac{1}{t} \quad \Leftrightarrow \quad u = \cfrac{1}{\cfrac{1}{f_{\rm SL}} + \cfrac{1}{t}} \tag{4.3.13} \] です。 | |
 | 共役関係が連続しているイメージか。あと、 \[ \begin{align*} f_{\rm CL} - p = s - t \\ \Leftrightarrow \quad t &= s - f_{\rm CL} + p \\ &= \frac{x f_{\rm CL}}{x + f_{\rm CL}} - f_{\rm CL} + f_{\rm SL} \frac{1 - \beta}{\beta} \\ &= f_{\rm SL} \frac{1 - \beta}{\beta} - \frac{{f_{\rm CL}}^2}{x + f_{\rm CL}} \tag{4.3.14} \end{align*} \] と、 \[ q = u - y \quad \Leftrightarrow \quad y = u - q = \cfrac{1}{\cfrac{1}{f_{\rm SL}} + \cfrac{1}{t}} - f_{\rm SL} \left( 1 - \beta \right) \tag{4.3.15} \] も成立しそうですね。 | |
 | というわけで、式4.3.14と式4.3.15から、アパーチャーの像の位置\(y\)と、アパーチャー~シリンダー・レンズの主点の距離\(x\)の関係が分かったわけです。 | |
 | 他にもパラメータがいっぱいありますけど?? | |
 |
確かにそうですが、LSUの場合、\(f_{\rm CL}\)や\(f_{\rm SL}\)にたくさんバリエーションがあるわけではないので、例えば\(f_{\rm CL}\)=72mm、\(f_{\rm SL}\)=70mmとしておきましょう(A3サイズ)。そうすると、走査レンズの倍率\(\beta\)に応じて、図4.3.5のようなグラフが得られます。
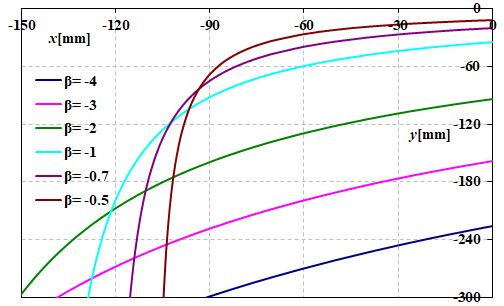 図4.3.5 アパーチャーの像の位置(\(f_{\rm CL}\)=72mm、\(f_{\rm SL}\)=70mm) |
|
 | う~ん。でも、結局Fraunhofer回折とFresnel回折の境界線の問題は未解決のままですよ。 | |
 |
ここからは経験的な話になりますね。だいたい、\(y\)の絶対値が60mmまでの領域だとFresnel回折で計算した方がよいと思います。
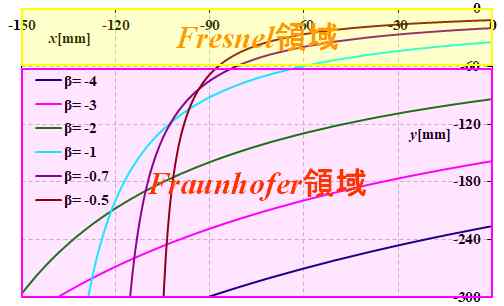 図4.3.6 Fraunhofer回折とFresnel回折の境界線 |
|
 | アパーチャー~シリンダー・レンズの主点の距離(\(x\))って、いろいろあり得るんですか?? | |
 | いたずらに\(x\)を大きくするとLSUのサイズが大きくなりますからね。と言って、逆に\(x\)を小さくしすぎると、例えば光源をマルチビームに展開したときに、いろいろと不具合が生じます。この辺は、少しややこしい話になるので省きますが、一般的に\(x\)は\(f_{\rm CL}\)から大きく外れない範囲で設定しますね。 | |
 | そうすると、何となく\(\beta\)で分類できそうですね。\(\beta\)の絶対値が\(1\)以上だとFraunhofer回折、\(1\)未満だとFresnel回折みたいな。 | |
 | そうですね。非常に大雑把な考え方ですが、まずは\(\beta\)に着目して、どちらで計算するかの目安にするのは、それほど的外れではないと思います。ちなみに、\(\beta\)の絶対値が\(1\)以上の走査光学系のことを拡大系、\(1\)未満の走査光学系のことを縮小系と言ったりしますね。 | |
 |
つまり、 拡大系 ⇔ \(\left| \beta \right| \ge 1\) ⇔ Fraunhofer回折 縮小系 ⇔ \(\left| \beta \right| < 1\) ⇔ Fresnel回折 ってことか。そうすると、どうやって縮小系 or 拡大系を見極めるか、知りたくなりますね。 |
|
 |
\(\beta\)は、走査レンズがポリゴン・ミラーと感光体の間にどうレイアウトされているかでほぼ決定されてしまうので、そんなに難しくないです。
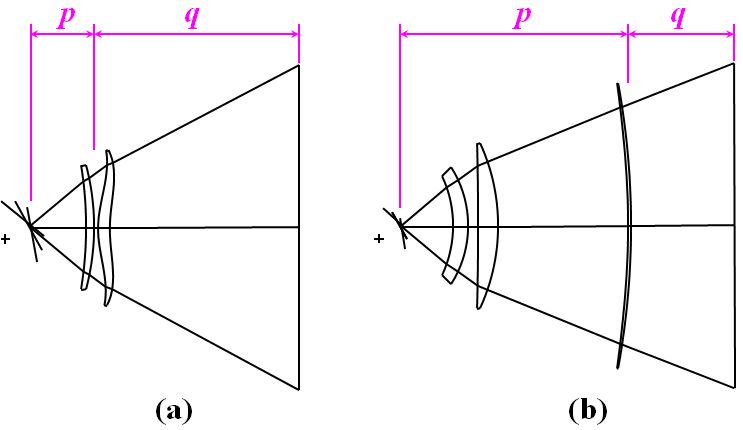 図4.3.8 走査光学系のタイプ(a:拡大系、b:縮小系) 基本的に走査レンズのレイアウト(図4.3.8)は、(a)のようにすべてのレンズをポリゴン・ミラー側に寄せるタイプと、(b)のように1つだけ感光体側に寄せるタイプの、大きく2つに分類できます。(a)のタイプは、\(p < q\)なので拡大系になりますし、(b)のタイプは、感光体側に寄せたレンズに強いパワーを持ってきますので、\(p > q\)となり縮小系です。 |
|
 | レイアウトを見たら、たいていどっちの回折計算でやるべきかという方針が立つわけですね。でも、どうして(a)とか(b)のようなタイプがあるんですか?? | |
 | 縮小系はあらゆるものが縮小されるので、例えば走査レンズの加工誤差や取付誤差などの影響も縮小されます。ですから、非常に安定した光学系を提供できる。一方、拡大系は、最後の走査レンズ~感光体の間隔が広くとれるので、その空間に折返しミラーを配置してLSUの立体的なサイズをコンパクトにまとめやすい。だから、レイアウトが容易になるというメリットがあります。 | |
 | なるほど。どちらのタイプでLSUを設計するかは、機種に求められるコンセプトに依存するわけですね。 |
| 前頁へ | 戻る | 次頁へ |