 | ここまでは、回折を考慮すべき開口の数は1つだけでした。でも、開口は複数あっても構いません。 | |
 | そりゃそうかもしれないけど、面倒な話になりそうな予感。 | |
 |
そうでもないですよ。基本的には、それぞれの寄与を重ね合わせればいいので、考え方は単純です。そのための準備として、開口を平行移動したときの回折パターンについて議論することにしましょう。
 図4.4.1 開口の平行移動 |
|
 | Fraunhofer回折での議論に限定ですか?? | |
 | そうですね。Fresnel回折は大幅に端折ったので、そうしましょう。 | |
 | 平行移動だけだったら、座標変換で済みそうですね。平行移動した開口の中心\(\left( \xi_1, \eta_1\right)\)を通る新しい\(\xi^{\thinspace \prime}\eta^{\thinspace \prime}\)座標系を設定すれば、 \[ U_1 \left( \mu, \nu \right) = C_0 \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} g \left( \xi^{\thinspace \prime}, \eta^{\thinspace \prime} \right) \mathrm{e}^{-2 \pi i \left( \mu \xi^{\thinspace \prime} + \nu \eta^{\thinspace \prime} \right) } d \xi^{\thinspace \prime} d \eta^{\thinspace \prime} \tag{4.4.1} \] だし。 | |
 | \(\xi^{\thinspace \prime}=\xi_1+\xi\)、\(\eta^{\thinspace \prime}=\eta_1+\eta\)だから?? | |
 | ん〜と。\(d\xi^{\thinspace \prime}=d\xi\)、\(d\eta^{\thinspace \prime}=d\eta\)を考慮して、 \[ \begin{align*} U_1 \left( \mu, \nu \right) &= C_0 \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} g \left( \xi^{\thinspace \prime}, \eta^{\thinspace \prime} \right) \mathrm{e}^{-2 \pi i \big[ \mu \left( \xi_1 + \xi \right) + \nu \left( \eta_1 + \eta \right) \big] } d \xi d \eta \\ &= C_0 \mathrm{e}^{-2 \pi i \left( \mu \xi_1 + \nu \eta_1 \right) } \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} g \left( \xi^{\thinspace \prime}, \eta^{\thinspace \prime} \right) \mathrm{e}^{-2 \pi i \left( \mu \xi + \nu \eta \right) } d \xi d \eta \tag{4.4.2} \end{align*} \] かな。 | |
 | \(g\)は瞳関数ですからね。開口の内部のとき\(1\)、外部のとき\(0\)と定義していたにすぎないことを思い出せば、式4.4.2において\(g\left(\xi^{\thinspace \prime},\eta^{\thinspace \prime}\right)\)を改めて\(g\left(\xi,\eta\right)\)としてもいいでしょう。 | |
 | そうすると、 \[ U_1 \left( \mu, \nu \right) = C_0 \mathrm{e}^{-2 \pi i \left( \mu \xi_1 + \nu \eta_1 \right) } \mathcal{F} \big[ g \left( \xi, \eta \right) \big] \tag{4.4.3} \] ですね。 | |
 | 同一開口が\(M\)個あった場合、それぞれの開口の中心を\(\left(\xi_j,\eta_j\right)\)とすれば、それぞれの回折パターンは式4.4.3から、 \[ U_j \left( \mu, \nu \right) = C_0 \mathrm{e}^{-2 \pi i \left( \mu \xi_j + \nu \eta_j \right) } \mathcal{F} \big[ g \left( \xi, \eta \right) \big] \tag{4.4.4} \] ですから、全体としての回折パターンは、 \[ U \left( \mu, \nu \right) = C_0 \mathcal{F} \big[ g \left( \xi, \eta \right) \big] \sum_{j=1}^{M} \mathrm{e}^{-2 \pi i \left( \mu \xi_j + \nu \eta_j \right) } \tag{4.4.5} \] となるわけです。 | |
 | これは振幅分布だから、強度分布は2乗すればいい?? | |
 | はい。 | |
 | ということは、 \[ I \left( \mu, \nu \right) = \Big| U \left( \mu, \nu \right) \Big|^2 = {C_0}^2 \Big| \mathcal{F} \big[ g \left( \xi, \eta \right) \big] \Big|^2 \sum_{j=1}^{M} \sum_{k=1}^{M} \mathrm{e}^{-2 \pi i \big[ \mu \left( \xi_j - \xi_k \right) + \nu \left( \eta_j -\eta_k \right) \big] } \tag{4.4.6} \] ってことか。 | |
 | ここで、\(\mu=\nu=0\)の強度を\(I_0\)とすれば、 \[ I_0 = {C_0}^2 \Big| \mathcal{F} \big[ g \left( \xi, \eta \right) \big]_{\mu = \nu =0} \Big|^2 M^2 \tag{4.4.7} \] です。更に、開口の内部の振幅が均一分布であれば、\(\mu=\nu=0\)のとき、 \[ \mathcal{F} \big[ g \left( \xi, \eta \right) \big]_{\mu = \nu = 0} = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} g \left( \xi, \eta \right) d \xi d \eta = \iint_B d \xi d \eta = S \tag{4.4.8} \] ですから(\(S\)は開口Bの面積)、式4.4.6は、 \[ I \left( \mu, \nu \right) = \frac{I_0}{S^2 M^2} \Big| \mathcal{F} \big[ g \left( \xi, \eta \right) \big] \Big|^2 \sum_{j=1}^{M} \sum_{k=1}^{M} \mathrm{e}^{-2 \pi i \big[ \mu \left( \xi_j - \xi_k \right) + \nu \left( \eta_j -\eta_k \right) \big] } \tag{4.4.9} \] と書けるというわけです。 |
〜多重スリット〜
 |
ここで、この開口を\(2a\times 2b\)の矩形開口とし、間隔\(2\Delta\)で\(M\)個並列していることを考えてみましょう。
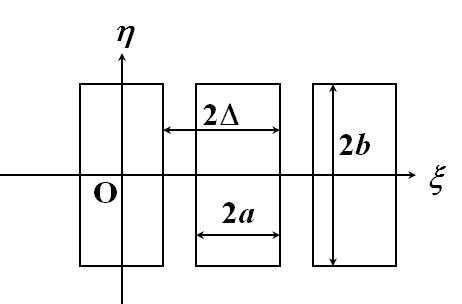 図4.4.2 多重スリット このときの回折パターンはどうなりますか?? |
|
 | う〜ん。それぞれの開口の中心\(\left(\xi_j,\eta_j\right)\)のうち、\(\eta_j\)は\(\eta_1\)と同じですよね。 | |
 | そうですね。では、\(\eta_1=0\)とし、回折パターンも\(\xi\)軸に沿った(\(\eta=0\))強度分布として考えましょう。 | |
 | \(\xi_j\)は\(2\Delta\left(j-1\right)\)だから、式4.4.5から、 \[ \begin{align*} U \left( \mu \right) &= C_0 \mathcal{F} \big[ g \left( \xi \right) \big] \sum_{j=1}^{M} \mathrm{e}^{-2 \pi i \mu \times 2 \Delta \left( j - 1 \right) } = C_0 \mathcal{F} \big[ g \left( \xi \right) \big] \frac{ \mathrm{e}^{-2 \pi i \mu 2 \Delta M } - 1 }{ \mathrm{e}^{-2 \pi i \mu 2 \Delta } - 1 }\\ &= C_0 \mathcal{F} \big[ g \left( \xi \right) \big] \frac{ \mathrm{e}^{-2 \pi i \mu \Delta M } }{ \mathrm{e}^{-2 \pi i \mu \Delta } } \frac{ \mathrm{e}^{-2 \pi i \mu \Delta M } - \mathrm{e}^{2 \pi i \mu \Delta M } }{ \mathrm{e}^{-2 \pi i \mu \Delta } - \mathrm{e}^{2 \pi i \mu \Delta } }\\ &= C_0 \mathcal{F} \big[ g \left( \xi \right) \big] \frac{ \mathrm{e}^{-2 \pi i \mu \Delta M } }{ \mathrm{e}^{-2 \pi i \mu \Delta } } \frac{ \sin 2 \pi \mu \Delta M }{ \sin 2 \pi \mu \Delta } \tag{4.4.10} \end{align*} \] ですね。 | |
 | 強度分布は?? | |
 | 式4.4.10を2乗すればいいだけだから、 \[ I \left( \mu \right) = \Big| U \left( \mu \right) \Big|^2 = {C_0}^2 \Big| \mathcal{F} \big[ g \left( \xi \right) \big] \Big|^2 \left( \frac{ \sin 2 \pi \mu \Delta M }{ \sin 2 \pi \mu \Delta } \right)^2 \tag{4.4.11} \] では?? | |
 | そうなんですが、式4.4.7と同様に\(\mu=0\)の強度を\(I_0\)とすれば、 \[ I_0 = {C_0}^2 \Big| \mathcal{F} \big[ g \left( \xi \right) \big]_{\mu = 0} \Big|^2 M^2 \] ですし、開口の内部の振幅が均一分布であれば、 \[ \mathcal{F} \big[ g \left( \xi \right) \big]_{\mu = 0} = \int_{-\infty}^{\infty} g \left( \xi \right) d \xi = \int_{-a}^{a} d \xi = 2a \] です。また、このケースだと、\(g\left(\xi\right)\)のFourier変換が計算できますね。 | |
 | ん??そっか。 \[ \mathcal{F} \big[ g \left( \xi \right) \big] = \int^{\infty}_{-\infty} g \left( \xi \right) \mathrm{e}^{-2 \pi i \mu \xi} d \xi = \int^a_{-a} \mathrm{e}^{-2 \pi i \mu \xi} d \xi = \left[ \frac{ \mathrm{e}^{ -2 \pi i \mu \xi } }{ -2 \pi i \mu } \right]_{-a}^a = \frac{ \sin{ 2 \pi \mu a } }{ \pi \mu } \] 結局、まとめると式4.4.11は、 \[ \begin{align*} I \left( \mu \right) &= \frac{I_0}{\left( 2 a \right)^2 M^2} \left( \frac{ \sin 2 \pi \mu a }{ \pi \mu } \right)^2 \left( \frac{ \sin 2 \pi \mu \Delta M }{ \sin 2 \pi \mu \Delta } \right)^2 \\ &= I_0 \left( \frac{ \sin 2 \pi \mu a }{ 2 \pi \mu a } \right)^2 \left( \frac{ \sin 2 \pi \mu \Delta M }{ M \sin 2 \pi \mu \Delta } \right)^2 \tag{4.4.12} \end{align*} \] ってことか。 | |
 | 式4.4.12の右辺第1項は、式4.2.17と同じなので、スリット1つあたりの回折像の寄与分を示しています。 | |
 | あ、本当だ!! | |
 | よって、右辺第2項が、多重スリットの干渉縞の寄与分ということになります。これを、\(I_s\left(\mu\right)\)としておきましょう。 \[ I_s \left( \mu \right) = \left( \frac{ \sin 2 \pi \mu \Delta M }{ M \sin 2 \pi \mu \Delta } \right)^2 \tag{4.4.13} \] | |
 | なるほど。 | |
 |
\(M\)を変えて回折パターンを計算した結果が図4.4.3です(\(I_0\)を正規化している)。
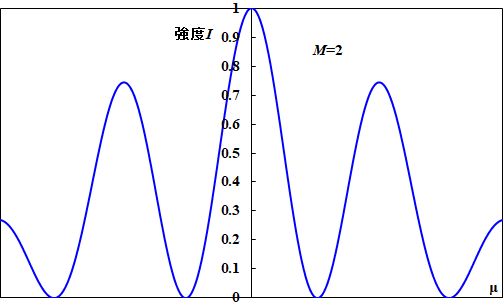 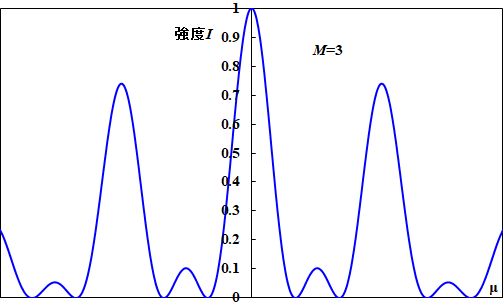 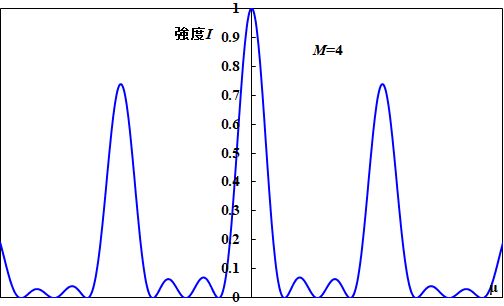 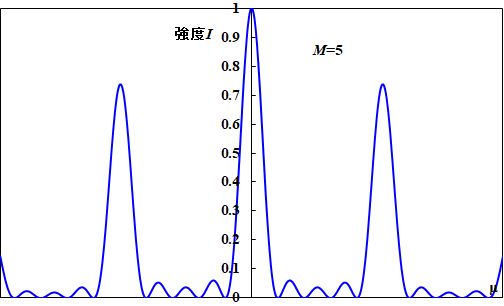 図4.4.3 多重スリットの回折パターン(\(M=2\sim5\)) |
|
 | 何か、特徴がありそうですね。 | |
 | 例えば?? | |
 | 山がいっぱいあるけど、\(M=3\)以上は、大きい山の間に小さい山がポコポコあるような感じ?? | |
 | 数に注目すると?? | |
 | 「小さい山の数=\(M-2\)」という関係がありそうですね。 | |
 | 大きい山については何か言えませんか?? | |
 | う〜ん―。そうか。大きい山の位置は\(M\)によらず同じかな。 | |
 | 山の幅についてはどうですか?? | |
 | あ〜。\(M\)が大きくなると、狭くなっていってますね。 | |
 | そうですね。多重スリットによる回折パターンの特徴としては、そんなところでしょう。ちなみに、大きい山の位置は、 \[ \frac{ \sin 2 \pi \mu \Delta M }{ M \sin 2 \pi \mu \Delta } = 1 \] の解として与えられ、整数を\(m\)とおいて、 \[ \mu_m = \frac{ m }{ 2 \Delta } \tag{4.4.14} \] となります。この\(m\)は回折次数と呼ばれます。さて、先程も言ったように、式4.4.12は、スリット1つあたりの回折像の寄与分と、多重スリットの干渉縞の寄与分の複合したものです。 | |
 | そうでしたね。 | |
 | とすると、第1項の寄与分は、式4.2.18を満たす条件で、強度は\(0\)になります。一方、第2項の寄与分について、強度が極大になる位置を求めてみましょう。 | |
 | それは、式4.4.13を微分して、 \[ \begin{align*} \frac{\partial I_s}{\partial \mu} &= 2 \frac{\sin 2\pi\mu \Delta M}{M \sin 2\pi\mu \Delta} \left[\frac{2\pi\Delta M \cos 2\pi\mu \Delta M}{M \sin 2\pi\mu \Delta}-\frac{2\pi \Delta \sin 2\pi\mu \Delta M \cos 2\pi\mu \Delta}{M \sin^2 2\pi\mu \Delta}\right] \\ &= \frac{4 \pi \Delta \sin 2\pi\mu \Delta M}{M^2 \sin^3 2\pi\mu \Delta} \left(M \sin 2\pi\mu \Delta \cos 2\pi\mu \Delta M - \sin 2\pi\mu \Delta M \cos 2\pi\mu \Delta \right) \\ &= 0 \end{align*} \] を解けばいいのでは?? | |
 | そうすると、極大の位置は、整数を\(P\)としたとき、 \[ M \sin 2\pi\mu_P \Delta \cos 2\pi\mu_P \Delta M - \sin 2\pi\mu_P \Delta M \cos 2\pi\mu_P \Delta = 0 \tag{4.4.15} \] を満たす\(\mu_P\)であることが分かります。 | |
 | う〜ん。でも、これは解けないのでは?? | |
 | いえ。式4.4.15は、 \[ \mu_P = \frac{P}{2\Delta} \tag{4.4.16} \] のときに、どんな\(M\)であっても満たされますよ。 | |
 | お〜。左辺の第1項も第2項も\(\sin\)の部分が\(0\)になるのか〜。 | |
 | そうすると、式4.2.18と式4.4.16から、 \[ \frac{N}{2a} = \frac{P}{2\Delta} \tag{4.4.17} \] のとき、\(\mu_N = \mu_P\)になりますから、式4.4.12の右辺第1項の極小値が、右辺第2項の極大値と一致することになり、その次数\(P\)の極大値がなくなってしまうことが分かります。 | |
 | 確かに。 | |
 | これを次数欠損と言います。 |
〜回折格子〜
 |
さて、この多重スリットの極限の形として、極めて多数の狭いスリットを等間隔に密に並べたものを考えてみましょう。
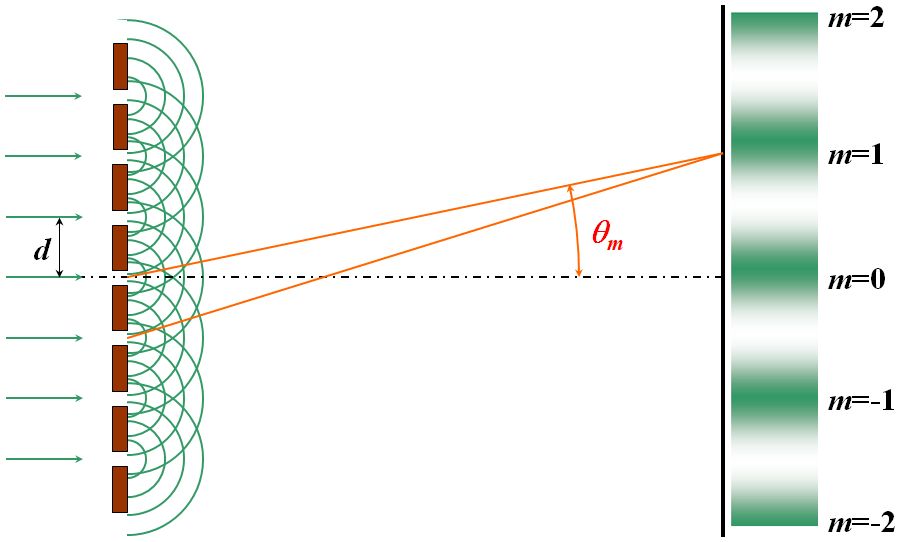 図4.4.4 回折格子(\(\theta_0=0\)) このような光学素子を回折格子と呼びます。 |
|
 | 高校生のときにやった記憶が…。 | |
 | 高校では干渉の事例の1つとして出てきたと思いますが、ここではFraunhofer回折の流れで見ています。当然、結果は同じになりますが、まず\(2\Delta=d\)として、更に入射角\(\theta_0\)、回折角\(\theta_m\)と置きましょう。そうすると、それぞれの方向余弦は\(l_0=\sin\theta_0\)、\(l_m=\sin\theta_m\)となりますから、式4.2.11は、 \[ \mu_m = \frac{ l_m - l_0 }{ \lambda } = \frac{ \sin \theta_m - \sin \theta_0 }{ \lambda } \tag{4.4.18} \] です。 | |
 | 式4.4.18を式4.4.12に代入すれば、回折格子の強度分布が得られるわけですね。 | |
 | また、そのピーク位置も式4.4.14と絡めて求めることができます。 | |
 | そっか。 \[ \frac{ m }{ d } = \frac{ \sin \theta_m - \sin \theta_0 }{ \lambda } \quad \Leftrightarrow \quad \sin \theta_m - \sin \theta_0 = \frac{ m \lambda }{ d } \tag{4.4.19} \] ってことですね。 | |
 | 高校のときは、たぶん\(\theta_0=0\)としていたでしょうから、 \[ \sin \theta_m = \frac{ m \lambda }{ d } \tag{4.4.20} \] で覚えていると思いますが。 | |
 | ウンウン。そんな式でしたね。 | |
 |
回折格子はアメリカのRittenhouseによって詳細に研究されました。
 David Rittenhouse(1732〜1796) |
|
 | ん??回折格子の強度分布を観察しようとすれば、開口ピッチ\(d\)はかなり狭くしないといけないですよね??18世紀にそんな技術があるとは思えないですけど…。 | |
 | Rittenhouseは髪の毛を無数に並べることで、回折格子を作成したんですよ。 | |
 | それは…。神経やられそうですね。 | |
 | 式4.4.20ですが、是非記憶に留めておいてほしいのは、波長\(\lambda\)と回折角\(\theta_m\)の関係です。波長が増加すると―。 | |
 | \(\sin\theta_m\)が増加するから\(\theta_m\)も増加する?? | |
 | はい。この関係は、この後で説明するDOEを理解するのにとても重要になってくるので忘れないでください。 |
| 前頁へ | 戻る | 次頁へ |