 | 回折現象と一般的なレンズの機能を融合させた光学素子のことを回折光学素子と呼びます。 | |
 | DOEって、diffractive optical elementの略?? | |
 |
そうですね。よく知られているのは、図4.5.1のようなレリーフ型と呼ばれるものです。
 図4.5.1 レリーフ型DOE |
|
 |
このタイプ、灯台で使われているレンズに似てますね。
 図4.5.2 御前崎の灯台レンズ |
|
 | Fresnelレンズですね。タイプとしては同じと考えても構わないですが、灯台のレンズとDOEは機能がまったく違いますね。 | |
 | どう違うんですか?? | |
 | 一般的に灯台のレンズは遠方の船舶に、海岸がここにあるぞ、っていうことを知らせることが目的ですから、集光させる機能だけあれば充分です。 | |
 | だったら、集光レンズを1つ用意して、クルクル回転させればいいのでは?? | |
 | ですが、そのレンズは巨大ですから、重量も相当なものになりますよね??クルクル回転させるのは容易ではありません。軽量化したくなります。 | |
 | なるほど。だから、集光レンズを輪切りにして、厚みを揃えて全体的に薄くしているわけか。 | |
 | そうです。 | |
 | ん??でも、ちょっと待てよ。この方法だと、厚みがなくなる分、各輪帯からの光線は1点に集光しないのでは?? | |
 | 集光するように、各輪帯の曲率半径を微調整すればいいだけの話です。 | |
 | じゃぁ、DOEの機能っていうのは?? | |
 | それについては追々迫っていくことにしましょう。まず、DOEの場合、輪切りにする厚さは、隣接する輪帯の境界で位相が整合している、という条件が付与されます。 | |
 | なぜですか?? | |
 |
この条件があると、見かけ上の波面がDOE全体で、あたかも揃っているように振る舞うからですよ。
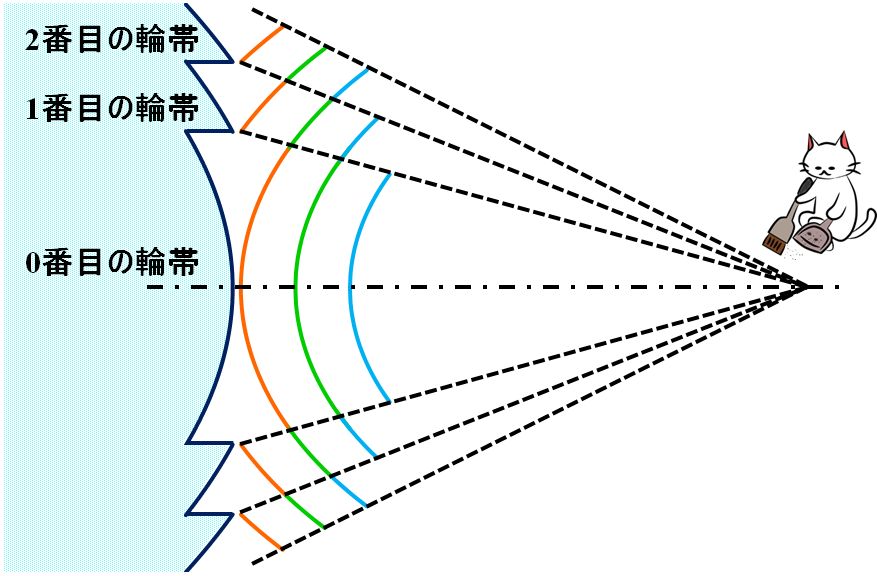 図4.5.3 DOEによって透過波面が形成されるイメージ |
|
 | つまり、DOEを透過した平面波は、DOEを出切ったときには橙色のようなギザギザした波面になっているけど、それよりも前の波面(緑色、青色、…)も同じようにギザギザしていて、それぞれは位相が整合しているから、0番目の輪帯の橙色の波面、1番目の輪帯の緑色の波面、2番目の輪帯の青色の波面、…が繋がって、連続した1つの波面のように見える、ってことか。 | |
 | 位相については光学的距離で議論する必要があるので、屈折率のある媒質中における光路長は幾何学的距離に屈折率を掛けないといけません。 | |
 | ということは、輪切りの厚さを\(d\)、屈折率を\(n\)とすると、隣接する輪帯の境界の光路長差\(\Delta l_0\)は―。 | |
 | と、その前に、DOEは波長との関係性を利用するので、このDOEは波長\(\lambda_0\)で威力を発揮すると仮定し、屈折率も\(n\left(\lambda_0\right)\)と書いておきましょう。ちなみに、この波長を設計波長と呼びます。 | |
 | そうすると、 \[ \Delta l_0 = n \left( \lambda_0 \right) d - d = d \bigl[ n \left( \lambda_0 \right) - 1 \bigr] \tag{4.5.1} \] として、位相整合条件は、 \[ \frac{2 \pi }{ \lambda_0} \Delta l_0 = 2 \pi \quad \Leftrightarrow \quad \frac{2 \pi }{ \lambda_0} d \bigl[ n \left( \lambda_0 \right) - 1 \bigr] = 2 \pi \tag{4.5.2} \] ってことか。 | |
 | ということで、\(d\)は、 \[ d \bigl[ n \left( \lambda_0 \right) - 1 \bigr] = \lambda_0 \quad \Leftrightarrow \quad d = \frac{ \lambda_0 }{ n \left( \lambda_0 \right) - 1 } \tag{4.5.3} \] と求まります。 | |
 | ムムム。厚さ\(d\)って、波長と同じレベルの寸法ってこと?? | |
 | そうですね。だから微細加工が必要になります。 | |
 | そうは言っても、レリーフ型DOEの輪帯が多くなると、端っこの方は加工が難しいと思いますけど。 | |
 |
鋭いですね。ですから、実用的にはレリーフ型DOEの輪帯の数は限界が存在すると考えていいでしょう。1つの解決策としては、輪帯の曲面を細かいステップで階段状にしてしまう、というのがあります。バイナリー型と言ったりしますね。或いは、いっそのこと、図4.5.4のようなステップ型DOEにしてしまう手もあります。こっちの方が加工は容易でしょう。
 図4.5.4 ステップ型DOE |
|
 |
ジェゼル王の階段ピラミッドみたいですね…。でも、このタイプだと、1つ1つの輪帯が平面だから、集光作用を持たないのでは??
 図4.5.5 ジェゼル王の階段ピラミッド |
|
 | 素子の反対側の面を曲面にすれば解決できますよ。 | |
 | 教授。もし、DOEに入射した光が、設計波長\(\lambda_0\)と違ってたらどうするんですか?? | |
 | いいところに気が付かれました。その場合には式4.5.2の位相整合条件が崩れてしまいます。この崩れ具合を\(\alpha\)とし、実際の入射光の波長を\(\lambda\)とすると、 \[ \frac{2 \pi }{ \lambda} d \bigl[ n \left( \lambda \right) - 1 \bigr] = 2 \pi \alpha \tag{4.5.4} \] と書けますね。 | |
 | 式4.5.2で両辺を割ると、\(\alpha\)が求まりそうですね。 | |
 |
\(n\left(\lambda\right)\)と\(n\left(\lambda_0\right)\)は\(\lambda\)の変化が極端でなければほぼ一致していると考えてよいので、
\[
\alpha = \frac{ n \left( \lambda \right) - 1 }{ \lambda } \cdot \frac{ \lambda_0 }{ n \left( \lambda_0 \right) - 1 } \approx \frac{ \lambda_0 }{ \lambda } \tag{4.5.5}
\]
という近似が成立します。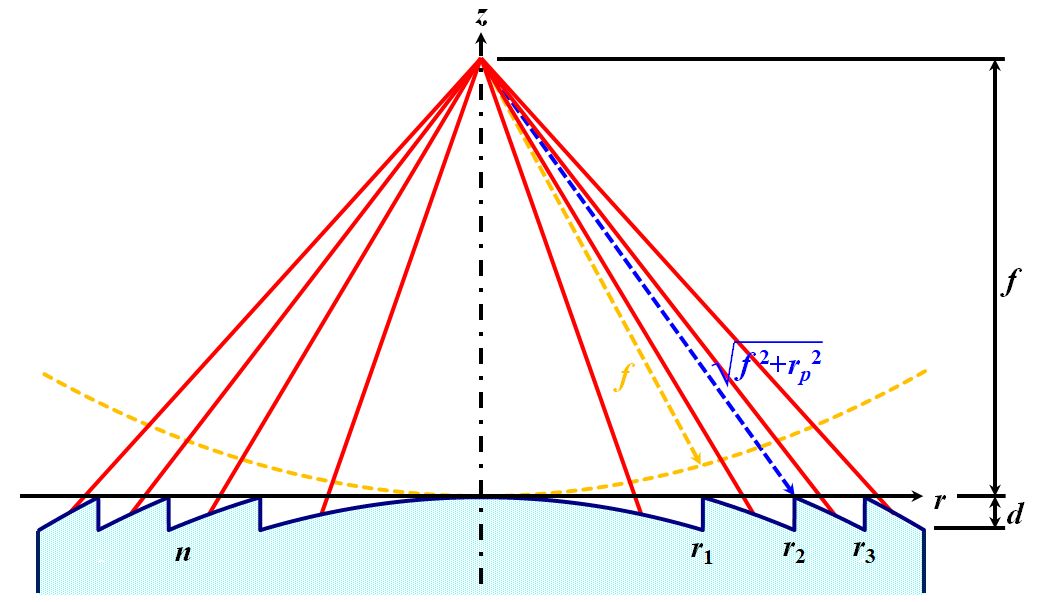 図4.5.6 DOEの基礎理論 さて、いよいよ核心(論文)に入っていきますが、まず図4.5.6のように座標を設定し、各輪帯の境界を\(r_1\)、\(r_2\)、…、\(r_p\)、…と置きます。また、\(z=f\)で集光する、としましょう。そうすると、\(p\)番目の輪帯の境界での位相整合条件は、 \[ \frac{ 2 \pi }{ \lambda_0 } \left( \sqrt{ f^2 + {r_p}^2 } - f \right) = 2 \pi p \tag{4.5.6} \] のように表記できます。\(f\)は\(r_p\)よりもずっと大きいと考え、括弧の中を近似してください。 |
|
 | ん〜と。 \[ \sqrt{ f^2 + {r_p}^2 } - f = f \sqrt{ 1 + \left( \frac{ r_p }{ f } \right)^2 } - f \approx f \left[ 1 + \frac{1}{2} \left( \frac{ r_p }{ f } \right)^2 \right] -f = \frac{ {r_p}^2 }{ 2 f } \] ですね。 | |
 | 式4.5.6に代入すると?? | |
 | こうかな。 \[ \frac{ 2 \pi }{ \lambda_0 } \times \frac{ {r_p}^2 }{ 2 f } = 2 \pi p \quad \Leftrightarrow \quad p = \frac{ {r_p}^2 }{ 2 \lambda_0 f } \tag{4.5.7} \] | |
 | \(p\)番目の輪帯は\(r_p \le r < r_{p+1}\)と書けますが、「\(r_p\)〜集光点」と「任意の\(r\)〜集光点」の光路長差\(\Delta L\left(r\right)\)は次のようになります。 \[ \begin{align*} \Delta L \left( r \right) &= \sqrt{ f^2 + {r_p}^2 } - \sqrt{ f^2 + r^2 } = f \sqrt{ 1 + \left( \frac{ {r_p} }{f} \right)^2 } - f \sqrt{ 1 + \left( \frac{ r }{f} \right)^2 } \\ &\approx f \left[ 1 + \frac{1}{2} \left( \frac{ r_p }{ f } \right)^2 \right] - f \left[ 1 + \frac{1}{2} \left( \frac{ r }{ f } \right)^2 \right] = \frac{ {r_p}^2 }{ 2 f } - \frac{ r^2 }{ 2 f } \tag{4.5.8} \end{align*} \] | |
 | 式4.5.7が使えそうですね。 | |
 | ついでに、 \[ \xi \equiv \frac{ r^2 }{ 2 \lambda_0 f } \tag{4.5.9} \] としておきましょう。 | |
 | そうすると、位相差\(\phi_p\left(r\right)\)は、 \[ \begin{align*} &\phi_p \left( r \right) = \frac{ 2 \pi }{ \lambda_0 } \Delta L \left( r \right) = \frac{ 2 \pi }{ \lambda_0 } \left( \frac{ {r_p}^2 }{ 2 f } - \frac{ r^2 }{ 2 f } \right) = 2 \pi \left( \frac{ {r_p}^2 }{ 2 \lambda_0 f } - \frac{ r^2 }{ 2 \lambda_0 f } \right)\\ &\Leftrightarrow \quad \phi_p \left( \xi \right) = 2\pi \left( p - \xi \right) \quad {\rm for} \quad p \leq \xi < p+1 \tag{4.5.10} \end{align*} \] ですね。 | |
 | 但し、この計算は設計波長\(\lambda_0\)の光波を前提としているので、もし波長\(\lambda\)の光波が入射したとすると、この位相は\(\alpha\)だけずれてしまいます。 | |
 | つまり、 \[ \phi_p \left( \xi \right) = \alpha 2\pi \left( p - \xi \right) \tag{4.5.11} \] ってことか。 | |
 | ここで吸収を無視できるとすれば、DOEの振幅透過率\(t\left(\xi\right)\)は、次のように定義されます。 \[ t \left( \xi \right) = \mathrm{e}^{ i \phi_p \left( \xi \right) } \quad {\rm for} \quad p \leq \xi < p+1 \tag{4.5.12} \] この関数は\(\xi\)の周期関数なので、複素Fourier級数展開できます。 | |
 | ん??Fourier…級数…展開…??複素…?? | |
 | 忘れてますね?? | |
 | 忘れてま〜す。 | |
 | 関数\(f\left(x\right)\)をFourier展開する、と言った場合、このケースだと、 \[ f \left( x \right) = \sum_{m=-\infty}^{\infty} c_m \mathrm{e}^{ i 2 \pi m x } \\ c_m = \int_{0}^{1} f \left( x \right) \mathrm{e}^{ -i 2 \pi m x } dx \] という公式を指します。\(c_m\)はFourier係数と言いますね。 | |
 | 公式さえあれば、こっちのもんですよ〜。そうすると、Fourier係数は、 \[ \begin{align*} c_m &= \int_{0}^{1} t \left( \xi \right) \mathrm{e}^{ -i 2 \pi m \xi } d \xi = \int_{0}^{1} \mathrm{e}^{ i \alpha 2\pi \left( p - \xi \right) } \mathrm{e}^{ -i 2 \pi m \xi } d \xi = \mathrm{e}^{ i 2\pi \alpha p } \int_{0}^{1} \mathrm{e}^{ -i 2\pi \bigl[ \left( \alpha + m \right) \xi\bigr] } d \xi \\ &= \frac{ -\mathrm{e}^{ i 2\pi \alpha p } }{ i 2 \pi \left( \alpha + m \right) } \left[ \mathrm{e}^{ -i 2 \pi \bigl[ \left( \alpha + m \right) \xi \bigr] } \right]_0^1 = \frac{ -\mathrm{e}^{ i 2\pi \alpha p } }{ i 2 \pi \left( \alpha + m \right) } \bigl[ \mathrm{e}^{ - i 2 \pi \left( \alpha + m \right) } -1 \bigr] \\ &= \mathrm{e}^{ i 2 \pi \alpha p } \mathrm{e}^{ - i \pi \left( \alpha + m \right) } \frac{ \mathrm{e}^{ i \pi \left( \alpha + m \right) }- \mathrm{e}^{ - i \pi \left( \alpha + m \right) }}{ i 2 \pi \left( \alpha + m \right) } = \mathrm{e}^{ i 2 \pi \alpha p } \mathrm{e}^{ - i \pi \left( \alpha + m \right) } \frac{ i 2 \sin \bigl[ \pi \left( \alpha + m \right) \bigr] }{ i 2 \pi \left( \alpha + m \right) } \\ \end{align*} \] \[ \begin{align*} \phantom{c_m} &= \mathrm{e}^{ i 2 \pi \alpha p } \mathrm{e}^{ - i \pi \left( \alpha + m \right) } \frac{ \sin \bigl[ \pi \left( \alpha + m \right) \bigr] }{ \pi \left( \alpha + m \right) } = \mathrm{e}^{ i 2 \pi \alpha p } \mathrm{e}^{ - i \pi \left( \alpha + m \right) } {\rm sinc} \bigl[ \pi \left( \alpha + m \right) \bigr] \tag{4.5.13} \end{align*} \] ですね。 | |
 | 結局、\(t\left(r\right)\)はどうなりますか?? | |
 | まず、\(t\left(\xi\right)\)が、 \[ t \left( \xi \right) = \sum_{m=-\infty}^{\infty} \mathrm{e}^{ i 2 \pi \alpha p } \mathrm{e}^{ - i \pi \left( \alpha + m \right) } {\rm sinc} \bigl[ \pi \left( \alpha + m \right) \bigr] \mathrm{e}^{ i 2 \pi m \xi } \] だから、式4.5.9を代入すれば、 \[ \begin{align*} t \left( \xi \right) &= \mathrm{e}^{ i 2 \pi \alpha p } \sum_{m=-\infty}^{\infty} \mathrm{e}^{ - i \pi \left( \alpha + m \right) } {\rm sinc} \bigl[ \pi \left( \alpha + m \right) \bigr] \exp \left( i 2 \pi m \frac{ r^2 }{ 2 \lambda_0 f } \right) \\ &= \mathrm{e}^{ i 2 \pi \alpha p } \sum_{m=-\infty}^{\infty} \mathrm{e}^{ - i \pi \left( \alpha + m \right) } {\rm sinc} \bigl[ \pi \left( \alpha + m \right) \bigr] \exp \left[ i \frac{ \pi }{ \lambda_0 \left( f / m \right) } r^2 \right] \tag{4.5.14} \end{align*} \] です。 | |
 | そうですね。そう、そうなんですが…。 | |
 | ん??計算、間違ってないですよ。何か歯切れが悪いですね。 | |
 | 式4.5.14は、直感的に少し気持ちの悪い表現になっているんですよ。 | |
 | そうですか??私は、ややこしい計算が終わって、気分は爽快ですけど。 | |
 | 式4.5.14の最後の指数関数は球面波を表しているんですが、普通、中心から四方八方に放射するような球面波のとき、位相はプラスってイメージがありませんか?? | |
 | ムムム。言われてみれば、確かに。 | |
 | ここまでのDOEの議論は、集光することを前提にしてましたよね?? | |
 | はい…。あ〜!!式4.5.14は放射のイメージになってる。 | |
 | そうなんです。このままだと、DOEだけ集光と放射の取り扱いを逆転させるという、かなり面倒な事態を招くことになります。 | |
 | それは、大怪我しそうですね。どうしましょう?? | |
 | この気持ち悪さを解消するには、\(m\)を\(-m\)に置き換えてしまうのが手っ取り早そうです。 | |
 | なるほど。どうせ、\(m\)は\(-\infty\)から\(\infty\)まで足しているだけだから、それを\(\infty\)から\(-\infty\)に代えても何の影響もないってことですね。 | |
 | よって、式4.5.14は、 \[ \begin{align*} t \left( \xi \right) &= \mathrm{e}^{ i 2 \pi \alpha p } \sum_{m=-\infty}^{\infty} \mathrm{e}^{ - i \pi \left( \alpha - m \right) } {\rm sinc} \bigl[ \pi \left( \alpha - m \right) \bigr] \exp \left[ - i \frac{ \pi }{ \lambda_0 \left( f / m \right) } r^2 \right] \\ &= \sum_{m=-\infty}^{\infty} c_m \exp \left[ - i \frac{ \pi }{ \lambda_0 \left( f / m \right) } r^2 \right] \tag{4.5.15} \end{align*} \] としておくと、今後の見通しがよくなります。 | |
 | なるほど〜。 | |
 | さて、ここで整理しておきましょう。式4.5.15は、設計波長\(\lambda_0\)で設計されたDOEの振幅透過率を表したものですが、一番最後の項は\(m\)番目の輪帯における球面波を示しています。 | |
 | はい。 | |
 | では、通常の焦点距離\(f\)のレンズだと、振幅透過率はどう書けるでしょう?? | |
 | \(m\)は、なくなりますよね。 | |
 | そうですね。 | |
 | 入射光の波長は\(\lambda\)ってことですか?? | |
 | そうです。 | |
 | だったら、 \[ t \left( \xi \right) \propto \exp \left( - i \frac{ \pi }{ \lambda f } r^2 \right) \tag{4.5.16} \] なのでは?? | |
 | そうすると、DOEというのは、 \[ \lambda {f_m}^{\left( {\rm zone} \right) } = \lambda_0 \frac{ f }{ m } \quad \Leftrightarrow \quad {f_m}^{\left( {\rm zone} \right) } = \frac{ \lambda_0 }{ \lambda } \frac{ f }{ m } \tag{4.5.17} \] という焦点距離\({f_m}^{\left( {\rm zone} \right) }\)のレンズが無数に集まったもの、とみなすことができます。 | |
 | なるほど。そういうイメージは、ありますね。 | |
 | また、DOEの\(m\)次の透過率\(\eta_m\)は、 \[ \eta_m = c_m {c_m}^{*} = {\rm sinc}^2 \bigl[ \pi \left( \alpha - m \right) \bigr] \tag{4.5.18} \] となります。これを\(m\)次回折光の回折効率と言います。 | |
 | ん??教授。入射光の波長が設計波長どおりだと\(\alpha=1\)だから、\(1\)次回折光の回折効率が\(\eta_1=\infty\)になっちゃうんですけど?? | |
 | \(\mathrm{sinc}\)関数は\(x=0\)のとき\(1\)と定義されるんですよ。 | |
 | そうなんですか?? | |
 | \(0 \le x < \cfrac{\pi}{2}\)のとき、一般に、 \[ \sin x < x < \tan x \] という式が成立するんですが、それぞれを\(\sin\)で割ります。 \[ 1 < \frac{ x }{ \sin x } < \frac { 1 }{ \cos x } \] 更に、逆数を取ると、 \[ 1 > \frac{ \sin x }{ x } > \cos x \] ここで、\(x\rightarrow0\)とすると、右辺は\(1\)に収束するので、\(\mathrm{sinc}\)関数は\(1\)に挟まれることになります。 | |
 | あ〜、だから\(1\)と定義するわけか。そうすると、\(1\)次回折光の回折効率は\(\eta_1=100\%\)なんですね。 | |
 |
そういうことです。従って、入射する波長が設計波長からずれると、\(1\)次回折光以外の回折光が発生し、\(\eta_1\)はどんどん低下していくことになります。
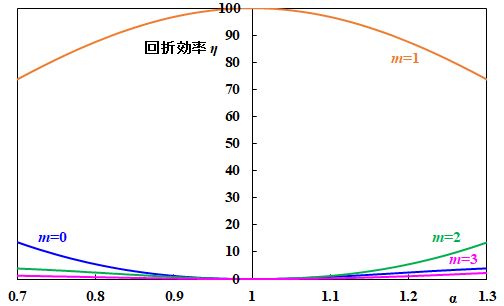 図4.5.7 \(m\)次回折光の回折効率 |
| 前頁へ | 戻る | 次頁へ |