 | 教授。このDOEを設計する場合、通常の幾何光学的な設計ツールを使うんですよね?? | |
 | 一般的には、そうなりますね。 | |
 | でも、通常の設計ツールは波動光学を考慮する仕様にはなってないですけど?? | |
 | そうですね。ですから、DOEの作用を受けて波面がどの方向に変化するか、という要素だけを加えて、あたかも幾何光学的に計算できるように割り切るのです。 | |
 | 回折光、いっぱい出てきますけど?? | |
 | 1つの回折次数に着目して、それぞれ計算するんですよ。 | |
 | え~、それは大変ですね。 | |
 | DOEを使うシーンというのは、一般的に回折次数を積極的に利用することが多いのです。例えば、この後で説明するケースでは\(1\)次回折光だけを利用し、それ以外の回折光は余計なものとして考えます。この場合、\(m=1\)だけ対象にして計算すればいいでしょう??また、物体を増やすケースでは複数の回折光を利用しますが、それにしたって、それぞれの回折次数で分けて考えた方が見通しがよくなります。 | |
 | 物体を増やす??分身の術?? | |
 |
そうです。iPhone ProにはLidarが搭載されてますが、これはVCSELの後ろにDOEを実装し、VCSELの発光点(=物体)を9倍に分身させているんですよ。
 図4.5.8 iPhoneのドット状のビーム |
|
 | お~。冗談で言ったのに。本当に分身の術ですね。でも、これで測距しても、粗っぽいポイント・クラウドしか得られないような…。 | |
 | iPhoneを動かせば解決できます。 | |
 | そういうことか。iPhoneだったら、手で持ってウロウロできますもんね。 | |
 | さて、光線追跡においては、入射光の方向ベクトルが境界面でどのように変換されるか、を計算できれば充分です。一般的にはSnellの法則が成立すればいいのですが、ここでは境界面の法線ベクトルを\(\vec{\mathstrut N}\)としておきましょう。また、光の方向ベクトル(=波数ベクトルの単位ベクトル)は、入射側を\(\vec{\mathstrut s_1}\)、出射側を\(\vec{\mathstrut s_2}\)、屈折率は、入射側を\(n_1\)、出射側を\(n_2\)とすると、Snellの法則はこう書けます。 \[ n_2 \vec{\mathstrut s_2} \times \vec{\mathstrut N} = n_1 \vec{\mathstrut s_1} \times \vec{\mathstrut N} \tag{4.5.19} \] | |
 | なるほど。外積で出てくるのは\(\sin\)ですもんね。 | |
 | これに対し、DOEの場合は新たな方向ベクトル\(\vec{\mathstrut s}_{\rm DOE}\)が出射光の方向ベクトルに加わると考えます。 | |
 | つまり、 \[ \big( n_2 \vec{\mathstrut s_2} + \vec{\mathstrut s}_{\rm DOE} \big) \times \vec{\mathstrut N} = n_1 \vec{\mathstrut s_1} \times \vec{\mathstrut N} \tag{4.5.20} \] かな。 | |
 | 方向ベクトルと波数ベクトルの関係は、式1.1.9から、 \[ \vec{\mathstrut k}_{\rm DOE} = \frac{ 2 \pi }{ \lambda} \vec{\mathstrut s}_{\rm DOE} \tag{4.5.21} \] と書けるので、式4.5.20は、 \[ \Big( n_2 \vec{\mathstrut s_2} + \frac{ \lambda }{ 2 \pi } \vec{\mathstrut k}_{\rm DOE} \Big) \times \vec{\mathstrut N} = n_1 \vec{\mathstrut s_1} \times \vec{\mathstrut N} \tag{4.5.22} \] となります。 | |
 | わざわざ波数ベクトルで書き直すんですか?? | |
 | こうしておくと、位相との関連で議論を展開することができるんですよ。 | |
 | 位相との関連?? | |
 | 位相と波数ベクトルの間には、 \[ \nabla \phi = - \vec{\mathstrut k} \tag{4.5.23} \] が成立します。 | |
 | ん~。式4.5.23って、式1.1.12の括弧の中が位相に相当するから、 \[ \nabla \phi = \nabla \big( \vec{\mathstrut k} \cdot \vec{\mathstrut r} - \omega t + \phi_0 \big) = \vec{\mathstrut k} \] ってことだと思うんですけど、符号が逆じゃないですか?? | |
 | 鋭いですね。 | |
 | でしょ?? | |
 | 例えば、単純な三角関数、 \[ u \left( \theta \right) = \cos \theta \] と、これに対して位相\(\phi\)(\(>0\))だけ進んでいる三角関数、つまり、 \[ u \left( \theta \right) = \cos \left( \theta + \phi \right) \] との関係を見てみましょう。この2つの関数をグラフにすると、どうなりますか?? | |
 |
ん~と。こうかな。
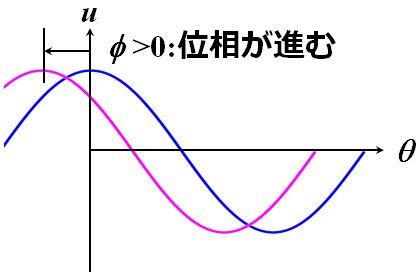 図4.5.9 位相が進む |
|
 | 図4.5.9を見ると、位相が進んでいるグラフの方が、見た目は後退してないですか?? | |
 | う~ん。確かに。 | |
 | 波数ベクトルからすると、マイナスですよね。 | |
 | つまり、「位相が進んでいる」というのと「波数ベクトルがプラスである」というのは、符号としては逆になるってことか。う~ん。分からなくはないけど、何だかややこしいですね。 | |
 | しかし、物理学的には式4.5.23のような形の方が、しっくりきますね。 | |
 | そうですか?? | |
 | 一般的に、スカラー・ポテンシャルとベクトル・ポテンシャルの関係は、力学の場合にせよ、電磁気学の場合にせよ、式4.5.23のような形で表現できます。 | |
 | 力学の場合、スカラー・ポテンシャルは位置エネルギーだから、高くなればなるほど大きくなるけど、ベクトル・ポテンシャルに相当する力そのものは、高い位置から低い位置に向かって大きくなるから、符号の関係が逆になる、ってイメージですね。 | |
 | というわけで、人によっては最初から位相の部分を、 \[ -\vec{\mathstrut k} \cdot \vec{\mathstrut r} + \omega t + \phi _0 \] と書くこともあります。 | |
 | どっちでもいい?? | |
 | はい。これは流儀の問題なので、重要なのは議論の中で一貫性があるかどうかだけです。 | |
 | てことは、教科書も?? | |
 | そうです。なので、どっちの流儀で書かれているかというチェックが、読む前に必要ですね。ガチガチの物理系の教科書なら、たいてい、このサイトの流儀で書かれていると思います。 | |
 | なら、混乱は避けられそうですね。 | |
 | 残念ながら、独立した波動・振動の教科書で俯瞰してみると、2つの流儀がせめぎ合ってますね。 | |
 | え~、面倒ですね…。 | |
 | さて、以上のことを踏まえると、DOEの場合、通常のレンズのようにレンズの形状(曲率半径や非球面係数)、厚さ、屈折率といった設計パラメータの代わりに、DOEとはどのような位相を付与する素子なのか、と捉えて位相\(\phi_{\rm DOE}\)を設計パラメータとして与えればよい、ということに気が付きませんか?? | |
 | つまり、DOEを幾何光学的に取り扱う場合には、DOEの実体がどうなっているかは、どうでもいいってこと?? | |
 | はい。そこで、いま考えているDOEは、\(m=1\)のときに光路差関数\(L_{\rm DOE}\)を付与すると仮定しましょう。そうすると、位相関数\(\phi_{\rm DOE}\)は…。 | |
 | その位相関数って、設計波長\(\lambda_0\)のときにDOEによって付与される、って考えればいいんですか?? | |
 | もちろんです。 | |
 | てことは、 \[ \phi_{\rm DOE} = \frac{ 2 \pi }{ \lambda_0 } L_{\rm DOE} \tag{4.5.24} \] かな?? | |
 | 式4.5.22~式4.5.24をまとめると?? | |
 | ん~と。 \[ \begin{align*} &\Big( n_2 \vec{\mathstrut s_2} - \frac{ \lambda }{ 2 \pi } \nabla \phi_{\rm DOE} \Big) \times \vec{\mathstrut N} = n_1 \vec{\mathstrut s_1} \times \vec{\mathstrut N} \\ &\Leftrightarrow \quad \Big( n_2 \vec{\mathstrut s_2} - \frac{ \lambda }{ 2 \pi } \frac{ 2 \pi }{ \lambda_0 } \nabla L_{\rm DOE} \Big) \times \vec{\mathstrut N} = n_1 \vec{\mathstrut s_1} \times \vec{\mathstrut N} \\ &\Leftrightarrow \quad \Big( n_2 \vec{\mathstrut s_2} - \frac{ \lambda }{ \lambda_0 } \nabla L_{\rm DOE} \Big) \times \vec{\mathstrut N} = n_1 \vec{\mathstrut s_1} \times \vec{\mathstrut N} \tag{4.5.25} \end{align*} \] あれ??でも、教授。この式って\(m=1\)が前提になっているじゃないですか。他の\(m\)のときは、どうなるんですか?? | |
 | 外積は\(\sin\)が関係してくるので、左辺の第2項の\(\nabla L_{\rm DOE}\)と\(\vec{\mathstrut N}\)の外積にも\(\sin\)が出てきますが、このときの角度は回折角\(\theta_m\)と考えてよいでしょう。一方で、式4.4.20にも\(\sin\theta_m\)が出てきますが、その値は回折次数\(m\)に比例していることが分かります。 | |
 | てことは、回折次数\(m\)を考慮する場合は、左辺の第2項を\(m\)倍すればいいってこと?? | |
 | そうですね。よって、DOEの光線追跡の式は、 \[ n_2 \vec{\mathstrut s_2} \times \vec{\mathstrut N} = \Big( n_1 \vec{\mathstrut s_1} + m \frac{ \lambda }{ \lambda_0 } \nabla L_{\rm DOE} \Big) \times \vec{\mathstrut N} \tag{4.5.26} \] となります。少し具体例を考えてみましょう。 | |
 | レリーフ型だと?? | |
 | レリーフ型というのは、平面を基板として、そこにDOEの要素が付与されていると考えることができます。 | |
 | ということは、入射光が平面波とすると、\(\vec{\mathstrut s_1}\)と\(\vec{\mathstrut N}\)は平行ってことだから、式4.5.26の右辺の第1項は\(0\)ですね。 | |
 | それが、「基板は平面である」ことを意味します。もしDOEの要素がなければ、右辺が\(0\)になりますから、\(\vec{\mathstrut s_2}\)は\(\vec{\mathstrut N}\)と平行ということになり、平面波のまま出射することになりますね。 | |
 | だけど、ここにDOEの要素が付与されているから、それを\(L_{\rm DOE}\)で表現できればいいわけですね?? | |
 | そうですね。 | |
 | と言っても、\(L_{\rm DOE}\)の表現形式が分からないですけど。 | |
 | 一般的な多項式でいいでしょう。 \[ L_{\rm DOE} = \sum_{j} a_j r^j \] 例えば、何か設計者の目的があって、それを実現するには曲率半径\(\rho\)=30mmのレンズを輪切りにしたDOEがベストだったと考えてみます。屈折率は設計波長のとき\(1.5\)としておきましょう。 | |
 | 教授。多項式で球面形状を表すのは、ちょっと無理があるのでは?? | |
 | 多項式の2次係数\(A\)を使って、球面の曲率半径を表現できますね。 \[ \rho = \frac{ 1 }{ 2 A } \tag{4.5.27} \] これは以前やりました。 | |
 | そうでしたっけ?? | |
 | 忘れているとは思ってましたけど。 | |
 |
さすが、教授。読んでますね~。そうすると、\(\rho\)=30mmだから、 \(A = \cfrac{1}{2 \times 30} = \cfrac{1}{60}\) で、更に式4.5.1を使って、 \(a_2 = \left( n - 1 \right) \times A = \left( 1.5 - 1 \right) \times \cfrac{1}{60} = \cfrac{1}{120}\) がDOEによって与えられる光路差関数の2次係数ですね。それ以外の係数は\(0\)です。 |
|
 | 惜しいですね。 | |
 | ん??惜しい?? | |
 | このDOEは集光する機能を有してますよね?? | |
 | ムムム。ひょっとして、正解は\(a_2 = -\cfrac{1}{120}\)だったりして?? | |
 | そうです。そうなります。 | |
 | ステップ型だと?? | |
 | 同じですね。ステップ型にするには、球面を基板として、その曲率半径を\(\rho\)としたとき、それとは逆のパワーとして作用するDOEの要素を付与すればよいのです。 | |
 | でも、式4.5.27って放物面としてDOEの要素を付与するわけだから、基板とうまく相殺しないのでは?? | |
 | 厳密に言えば。ですが、そのズレは無視できますね。だから、1つ1つのステップは平面と見なせます。もし、そのズレが気になるのであれば、基板としての球面も、放物面として与えれば済む話です。 | |
 | そうすると、ある面がDOEである、と言った場合、「基板の形状を与える」「設計波長を与える」「光路差関数の係数を与える」3種類のパラメータ群を設定する必要があるわけですね?? | |
 | もちろん、それで事足りるかどうかは使用するツールに依るので、説明書をしっかり読まないといけません。ひょっとしたら、光路差関数ではなく、位相関数で定義されているかもしれませんしね。 |
~負の分散~
 | で、結局、DOEってどういう使い方をするんですか?? | |
 | いろいろ使い道はありますよ。さっきも紹介しましたが、iPhone proのようにVCSELの発光部パターンを数倍に増やすのにDOEを使ったりね。ここでは、LSUでの使い道について紹介しましょう。 | |
 | はい。 | |
 | まず、従来のように通常のレンズだけでLSUを構成したとき、温度変化によって焦点距離がどのように振る舞うかを見てみましょう。ここでは、議論を簡単にするために、曲率半径\(\rho\)、屈折率\(n\)の平凸レンズを想定します。このとき、焦点距離\(f\)は、 \[ f = \frac{ \rho }{ n - 1 } \tag{4.5.28} \] のように表されます。 | |
 | 温度が上昇したら、形状が変化しそうですね。 | |
 | 曲率半径は?? | |
 | 膨張するから、大きくなるのでは?? | |
 | そうすると焦点距離は?? | |
 | 式4.5.28から、伸びますね。 | |
 | 次に考慮しないといけないのは何でしょう?? | |
 | 屈折率ですね。ん~、屈折率って温度が上昇すると、どうなるんだろう?? | |
 | 温度が高くなると膨張すると言いましたね。そうすると、密度はどうなります?? | |
 | 小さくなりますね。 | |
 | 密度と屈折率の間には式2.9.12のようなLorentz-Lorenzの式が成立しましたよね。 \[ \frac{n^2 - 1}{n^2 + 2} = \frac{N_A \alpha}{3 \varepsilon_0}\frac{d}{M} \tag{2.9.12} \] | |
 | う~ん。左辺は、\(n=1\)のときに\(0\)、\(n=\infty\)で\(1\)になるから、何となく単調増加って感じがしますね。てことは、密度が小さくなると、屈折率は小さくなりそうです。 | |
 | そうすると焦点距離は?? | |
 | 式4.5.28から、やっぱり伸びますね。 | |
 | 他には?? | |
 | ないですよ。だって、式4.5.28にはパラメータが2つしかないですもん。 | |
 | しかし、LSUは光源にLDを用いています。その発振波長が温度の影響を受けますよね?? | |
 | う…。確かに。 | |
 |
一般的なLDの発振波長と雰囲気温度の関係は、図4.5.10のようになっています。
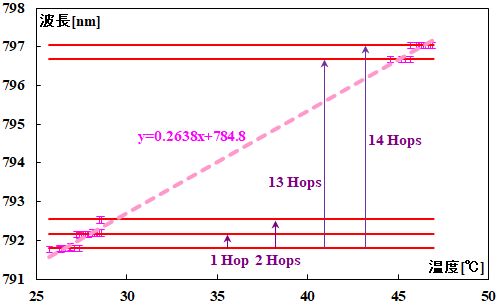 図4.5.10 発振波長の温度依存性 |
|
 | 全体的な傾向としては、温度が上昇すると発振波長は伸びていくんですね。でも、突然、ピョンピョンと不連続に変化するのが不思議~。 | |
 | 詳しい話はLDの中身に入っていくのでやめますが、これは発振波長の特徴的な傾向ですね。これをモード・ホップと言います。 | |
 | ホップ、ステップ、ジャンプってことか。屈折率が波長に依存するのは、式1.9.11のSellmeierの公式でやったけど、これを見ても、波長が増加したときに屈折率がどう振る舞うのかは、パッと分からないですね…。 \[ n^2 = A_0 + A_1 {\lambda}^2 + \frac{ A_2 }{ \lambda^2 } + \frac{ A_3 }{ \lambda^4 } + \frac{ A_4 }{ \lambda^6 } + \frac{ A_5 }{ \lambda^8 } \tag{1.9.11} \] | |
 |
よく使われる硝材や樹脂の場合は、図4.5.11のようになることが知られています。
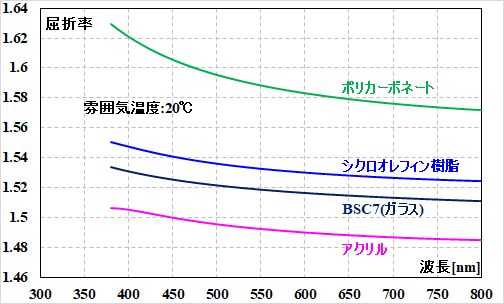 図4.5.11 屈折率の波長依存性 |
|
 | てことは、屈折率は小さくなるのか。そうすると、やっぱり焦点距離は伸びるわけですね。 | |
 | 要するに、通常のレンズの場合、温度が上昇すると焦点距離は長くなると言えそうです。 | |
 | 何か、ピンと来ましたよ。DOEはその逆になるってことでしょ?? | |
 | DOEと言っても、屈折による上記の性質がなくなるわけではありませんが、そこに新たな機能が付与されるイメージになりますね。このときに思い出してほしいのが、「波長が増加すると回折角\(\theta_m\)が増加する」という関係です。 | |
 |
そうすると、「温度が上昇する」⇒「波長が増加する」⇒「回折角が増加する」で、
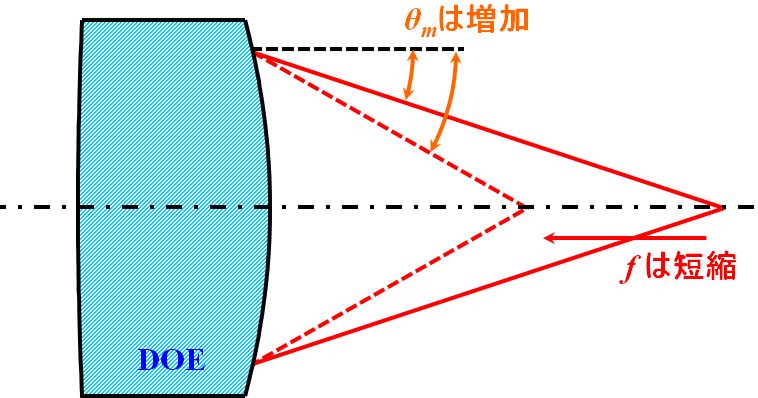 図4.5.12 DOEの焦点距離変動 図4.5.12のような感じになるから、焦点距離は短くなる、ってことですね。 |
|
 | よって、DOEに付与する機能を上手く設計すれば、温度が上昇しても焦点距離が変わらない光学システムがgetできます。 | |
 | お~!!それ、いいじゃないですか~!! | |
 | DOEの持つ「波長が増加する」⇒「焦点距離が短くなる」という非常に特徴的な機能は、負の分散と言ったります。 | |
 | 負の分散?? | |
 | まず、式4.5.28を\(n\)で微分してみましょう。 | |
 | それは簡単ですね。 \[ \frac{df}{dn} = - \frac{\rho}{\left( n - 1 \right)^2} = - \frac{f}{n-1} \] | |
 | つまり、 \[ \frac{df}{f} = - \frac{dn}{n-1} \] です。そこで、d線からC線に波長が変化したときの焦点距離変動、及びF線に波長が変化したときの焦点距離変動を引いたものを、その硝材の分散\(\mathfrak{D}_{\rm d}\)と定義します。 \[ \mathfrak{D}_{\rm d} = \frac{f_{\rm C} - f_{\rm d}}{f_{\rm d}} - \frac{f_{\rm F} - f_{\rm d}}{f_{\rm d}} = - \frac{n_{\rm C} - n_{\rm d}}{n_{\rm d} - 1} + \frac{n_{\rm F} - n_{\rm d}}{n_{\rm d} - 1} = \frac{n_{\rm F} - n_{\rm C}}{n_{\rm d} - 1} \tag{4.5.29} \] | |
 | わざわざ、C線とF線の2つを持ってきているのは何でですか?? | |
 | レンズ設計するときに対象とするのは、たいていの場合、可視光です。C線=656.273nm(赤色)、F線=486.133(青色)、d線=587.562nmなので、ちょうどd線がC線とF線の中間になりますし、赤色と青色の焦点距離変動が大きいのか小さいのかは、最も興味のある指標ですから、式4.5.29のように定義するのが合理的なんですよ。 | |
 | でも、d線じゃなくて、e線=546.074nmで議論することもありますよね?? | |
 | その場合には、C'線=643.847nmとF'線=479.991nmに変えます。 \[ \mathfrak{D}_{\rm e} = \frac{n_{\rm F^{\thinspace \prime}} - n_{\rm C^{\thinspace \prime}}}{n_{\rm e} - 1} \tag{4.5.30} \] | |
 | で、これがDOEだと?? | |
 | 前回、DOEとは式4.5.17で表される焦点距離のレンズが無数に集まったものとみなす、と言いましたが、この\({f_m}^{\left({\rm zone}\right)}\)を式4.5.28に適用します。 \[ \begin{align*} {f_m}^{\left( {\rm zone} \right) } = \frac{ \rho }{ n - 1 } \quad &\Leftrightarrow \quad n - 1 = \frac{ \rho }{ {f_m}^{\left( {\rm zone} \right) } } \\ &\Leftrightarrow \quad n = 1 + \frac{ \rho }{ {f_m}^{\left( {\rm zone} \right) } } = 1 + \rho \frac{ \lambda }{ \lambda_0 } \frac{ m }{ f } \\ &\Leftrightarrow \quad n = 1 + \beta_m \lambda \tag{4.5.31} \end{align*} \] ここで、 \[ \beta_m \equiv \frac{ \rho }{ \lambda_0 } \frac{ m }{ f } \tag{4.5.32} \] としましたが、そのうえで、式4.5.29に代入するんです。 | |
 | てことは、 \[ \begin{align*} {\mathfrak{D}_{\rm d}}^{\left( {\rm DOE} \right)} &= \frac{n_{\rm F} - n_{\rm C}}{n_{\rm d} - 1} = \frac{ \left( 1 + \beta_m \lambda_{\rm F} \right) - \left( 1 + \beta_m \lambda_{\rm C} \right) }{ \left( 1 + \beta_m \lambda_{\rm d} \right) - 1 } = \frac{ \beta_m \lambda_{\rm F} - \beta_m \lambda_{\rm C} }{ \beta_m \lambda_{\rm d} } \\ &= \frac{ \lambda_{\rm F} - \lambda_{\rm C} }{ \lambda_{\rm d} } \tag{4.5.33} \end{align*} \] かな。 | |
 | さて、\(\lambda_{\rm F} < \lambda_{\rm C} \)ですから、図4.5.10より屈折率は波長に対して減少関数になっているので\(n_{\rm F} > n_{\rm C} \)となり、式4.5.29から硝材の分散は正の値をとります。しかし、DOEの場合は式4.5.33から負の値になります。 | |
 | なるほど。だから負の分散ってことか。 | |
 | しかも、HOYAのBSC7という硝材を使って式4.5.29を計算してみると、\(n_{\rm F}=1.52237\)、\(n_{\rm d}=1.51680\)、\(n_{\rm C}=1.51432\)ですから\(\mathfrak{D}_{\rm d} = 0.015576\)になりますが、DOEの分散は式4.5.33より\({\mathfrak{D}_{\rm d}}^{\left( {\rm DOE} \right)} = -0.289569\)で桁が違うことも分かります。 | |
 | DOEの味付けは、ほんの少しでも結構スパイシーってことですね。 | |
 | この例では、DOEが1つしかないものとして取り扱ってきましたが、カメラ・レンズなどは可視光すべての面倒を見ないといけないので、硝材の違うDOEを貼り合わせたり、知らないところでDOEは活用されているんですよ。 | |
 | 製品をバラバラにしても、DOEが使われているかどうかは見落としそうですね。 | |
 |
肉眼で確認できなくはないですが、ある程度の目星が付いてないと、しんどいですね。だから、特許とか論文とかが重要なヒントになるわけです。例えば、図4.5.13はコリメーター・レンズをDOEにしたものですが、知らなければ見逃してしまうでしょう。
 図4.5.13 コリメーター・レンズをDOEにしたもの |
|
 | た、確かに…。でも、綺麗に溝が映ってますね。 | |
 |
LSUでは、㈱キヤノンが2002年に発売したLBP-2710に実装したのが最初だと思います。このときには、走査レンズに楕円のDOEを実装したんですよ。
 図4.5.14 LBP-2710 |
|
 | 走査レンズの有効範囲って広いから、それに溝を加工するのは大変ですね。 | |
 |
この機種以降、他のメーカーでもDOEが積極的に展開されて、図4.5.15のような光学素子(論文)まで登場しました。
 図4.5.15 コリメーター・レンズとシリンダー・レンズが一体になった光学素子 |
|
 | お~!!これは、凄いですね。試作品じゃないんですか?? | |
 |
とんでもない。この光学素子は、セイコーエプソン㈱が2003年に発売したLP-1400に実装されたのです。
 図4.5.16 LP-1400 なかなか凝った光学素子で、図4.5.17のような光路をとります。 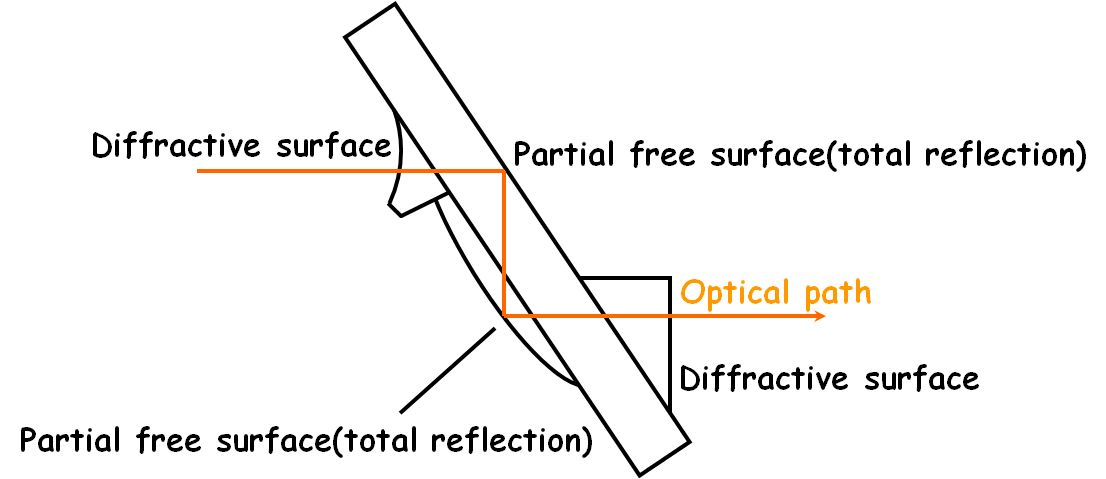 図4.5.17 光学素子の光路 |
|
 | え??DOEが2つ?? | |
 | そうです。入射面がコリメーター・レンズの機能を有する同心円のDOE、出射面がシリンダー・レンズの機能を有する直線のDOEとなっていて、途中2回の反射は全反射を利用しているという、かなりアクロバティックな設計になってます。 | |
 | へぇ~。 | |
 | LSUにおいて、コリメーター・レンズとシリンダー・レンズの変動が与える光学性能の劣化は莫迦にならなくて、そのため温度変化に弱い樹脂への変更はハードルの高い課題だったのです。しかし、DOEの実用化が進んで、この課題を解決することが可能になり、どちらのレンズも樹脂で成型することができるようになったわけです。 | |
 | で、だったら、いっそのこと2つのレンズを合体しちゃえと。 | |
 | そういうことです。実は目に見えないところで、こういう新しい技術的アイデアがどんどん産み出されているんですよ。 |
| 前頁へ | 戻る | 次頁へ |