 | 半導体によるレーザの原理というのは、どうなっているんですか?? | |
 | 発振プロセスを知るには、量子力学と物性物理の知識が必要になりますけど?? | |
 | ムムム。量子力学??かなり、怯みますけど。 | |
 | でしょうね。ですから、ここでは取り扱うことをやめておきます。それよりも、レーザから放射された後のビームの特性を知っておくことの方が重要です。 | |
 | なるほど。 | |
 | とは言うものの、概念的なことをザックリ知っておくのも無駄ではないので、少しだけ触れておきます。まず、半導体と光には密接な関係があるという点を押さえておきましょう。 | |
 |
そう言えば、太陽電池も半導体でしたね。
 図5.2.1 太陽電池 |
|
 |
はい。半導体に光が吸収されると光キャリア生成と呼ばれるプロセスが起こります。
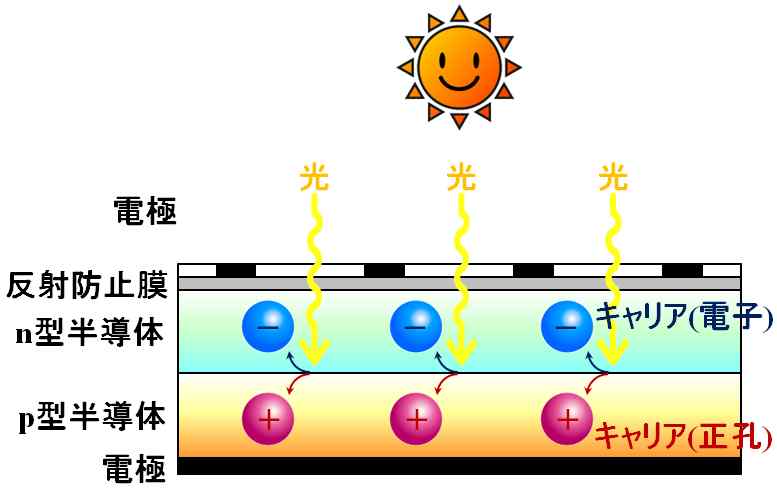 図5.2.2 光キャリア生成 |
|
 | それって、正孔と電子のペアが生まれるってこと?? | |
 | そうです。元々あったキャリアに、新たな光キャリアが生成されるので、電気が流れやすくなるわけです。光起電力効果と言ったりしますが、これが太陽電池の基本原理になります。そして、このプロセスは逆も成立します。 | |
 | つまり、正孔と電子のペアがくっついて光が生成する?? | |
 | これを放射再結合と言います。 | |
 | ということは、放射再結合を効率よく発生させれば、レーザはどんどん発振してくれるわけですね。 | |
 | 着眼点は正しいですね。しかし、これは言うほど簡単ではありません。 | |
 | なぜ?? | |
 |
非常に概念的な説明に留めますが、半導体における放射再結合というのは、穴のいっぱい空いた板の上をボールがたくさん転がっていて、ボールが穴の中にどれだけ入ったか、というモデルで理解できます。
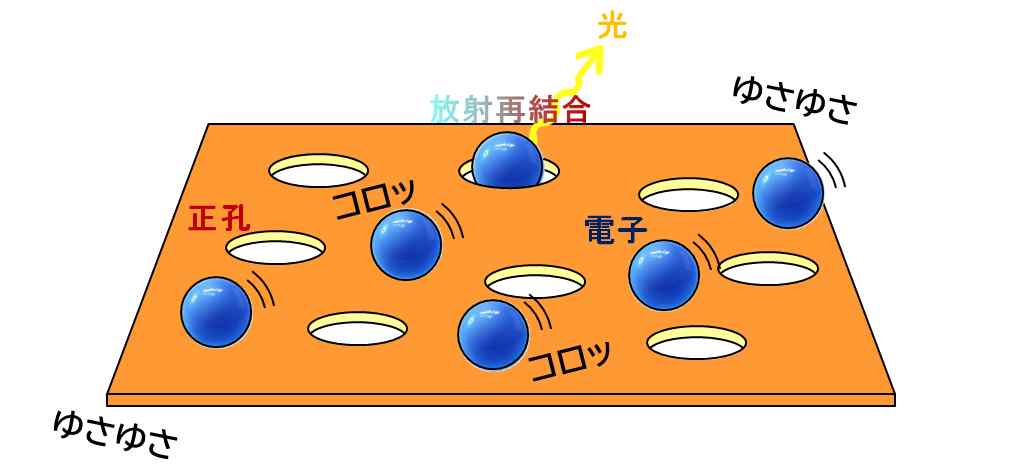 図5.2.3 放射再結合 |
|
 | パター・ゴルフみたいなもんか。穴が正孔で、ボールが電子のイメージですね。 | |
 |
一般に、温度が高くなると、この板が激しく揺れますし、ボールの運動も速くなりますから、穴を通過するボールの数は非常に少なくなります。しかも、周辺には何もないので、ボールはボロボロこぼれてしまいます。
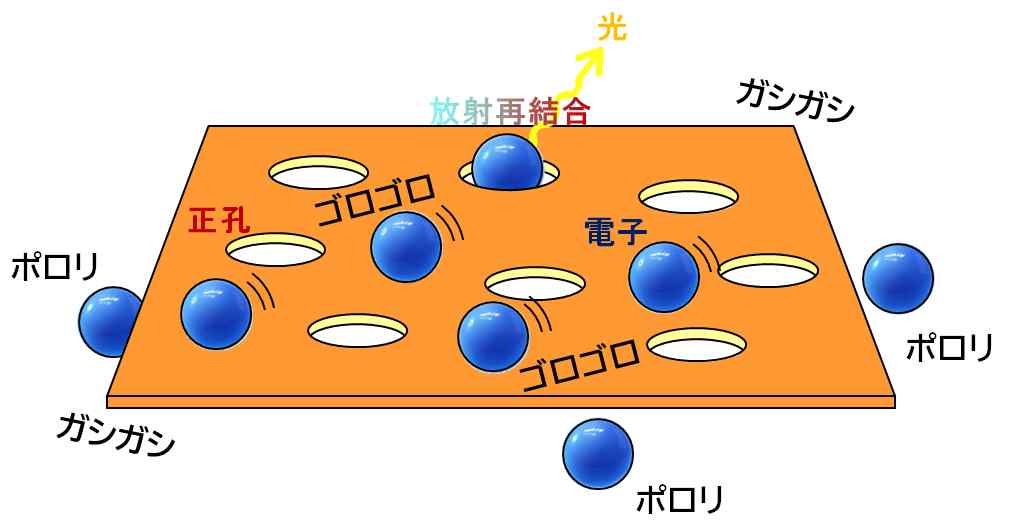 図5.2.4 温度が高い場合 |
|
 | だったら、ボールを次から次へ供給すればいいじゃないですか。 | |
 | つまり、大電流を供給するということですね??残念ながら、それだと発熱量も増大するので、半導体の接合部が溶けてしまいます。 | |
 | じゃ、全体的に冷やして、動きを鈍くすれば?? | |
 |
というわけで、最初のLDは77Kという極低温下で、しかもパルス発振させるのがやっとでした。これは1962年に、Hallの率いたチームによって実現(論文)されました。
 Robert Noel Hall(1919〜2016) |
|
 | でも、極低温じゃ、使い勝手が悪いですね。 | |
 |
そこで1963年、Kroemerがダブルヘテロ接合という概念(論文)を提唱します。
 Herbert Kroemer(1928〜) |
|
 | ヘテロ??ヘテロがダブル?? | |
 |
細かい話は端折りますが、感覚的には、図5.2.3の板の周囲に壁を設けるイメージですね。
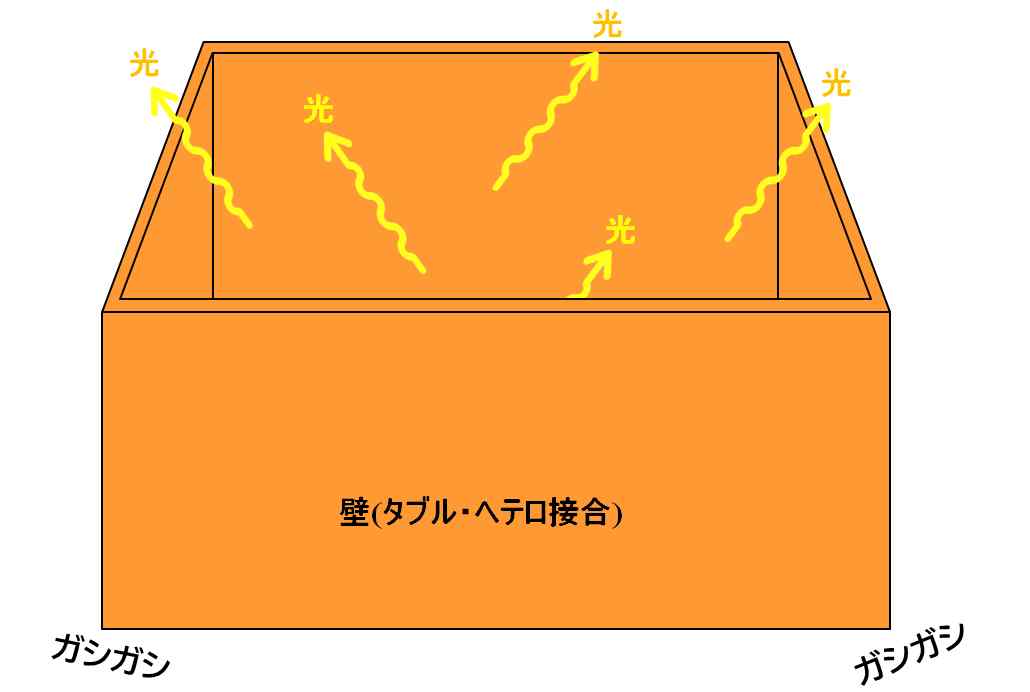 図5.2.5 ダブルへテロ接合の概念図 |
|
 | なるほど。ボロボロ落ちていたボールが、壁で遮られて穴の方に向かうようになるから、穴に落ちる確率が高くなっていくんですね。 | |
 |
あくまでイメージです。ところが、Kroemerがダブルへテロ構造を提案した当初は、技術的に実現するのは極めて難しいということで、学会での反応は非常に冷ややかなものだったと言われています。しかし、冷戦体制でアメリカと凌ぎを削っていた旧ソ連のAlferovがエピタキシャル成長の研究(論文)を発展させて、Kroemerのアイデアを実現するのです。エピタキシャル成長というのは、半導体の製造方法の一種で、簡単に言えばミルフィーユにする方法です。
 Zhores Ivanovich Alferov(1930〜2019) |
|
 | これで、室温環境下でのLDの発振が可能になったわけですね。 | |
 |
1970年は、Alferovだけではなく、ベル研にいたPanishも林先生と共同で、LDの室温環境下における連続発振に成功して(論文)おり、寧ろ実用的な観点からは、この二人の業績の方を重視する研究者も多いですね。
 Morton Panish(1929〜) |
|
 | やっぱり、研究とか開発って、論文にしろ特許にしろ、最初っていうのがとても重要なんですね。 | |
 |
ところで、室温で発振できるようになったLDですが、はやり温度が上昇していくと、電子が元気になって、せっかく作った壁を乗り越えてしまいます。
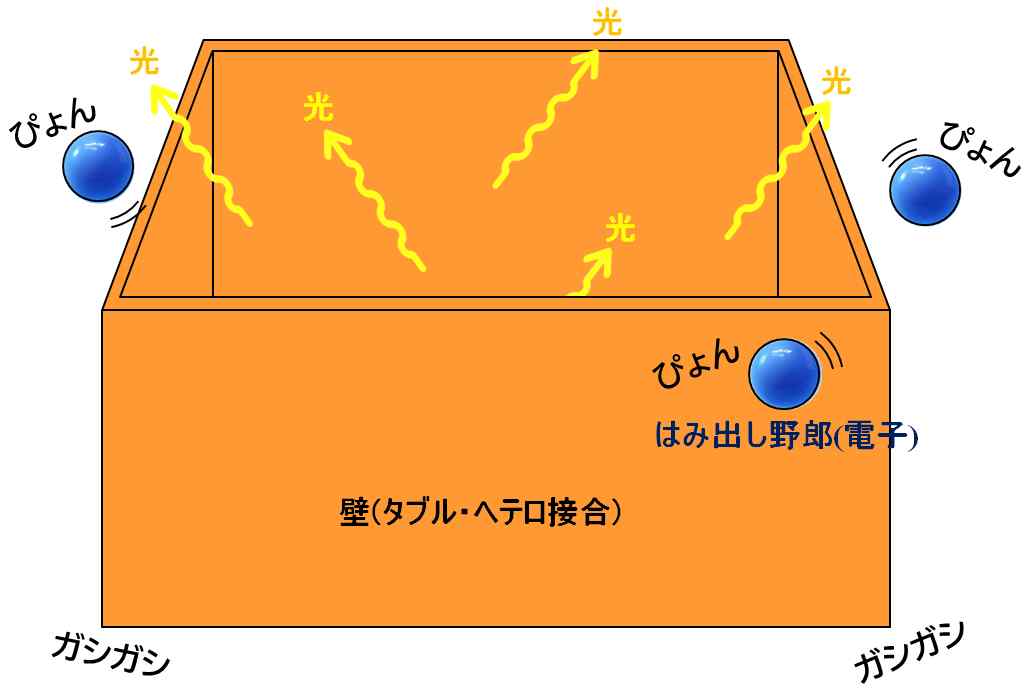 図5.2.6 温度が高い場合 |
|
 | そういう「はみ出し野郎」って、どこにでもいますね。 | |
 | 従って、温度が上昇すると、光量が落ちていきます。 | |
 |
う〜ん。確かに、言われてみればそうですね。前にLDを評価したとき、0℃と90℃では、同じ注入電流(\(I_f\))のままなのに、ビームの光量(\(P_0\))は90℃の方が落ちてました。そうか、そういうことか。
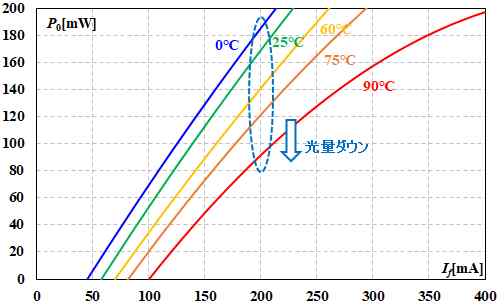 図5.2.7 注入電流、光量、温度の関係 |
|
 | あくまでイメージです。さて、LDの概念はここまでにして、次にLDから放射したビームの特性について議論しましょう。 |
〜Gaussianビームの特性〜
 | Gaussianビーム?? | |
 | ビームの最大の特徴と言ってもいいものですが、それは追々、明らかになります。 | |
 | てことは、また山ほど計算したりして?? | |
 | そうですね。なかなか、しんどい計算になるので、覚悟が必要です。 | |
 | え〜!! | |
 | ですが、なるべくショート・カットすることを目指しましょう。 | |
 | 教授。それ、ナイスです!! | |
 | さて、これまでは平面波、球面波をおもに扱ってきましたが、レーザの場合は、1つだけ制約条件を課します。 | |
 | 制約条件?? | |
 | そもそも、ビームはLDの活性層から放射されると説明しました。基本的には、放射されたビームは球面波になるだろうと予想されますが、活性層の内部ではビームがヘテロダイン構造によって閉じ込められているので、\(z\)方向(ビームの伝搬方向)の(複素)振幅の変化は制御されていると考えられます。 | |
 | それって、要するに裾が引っ張られているイメージですか?? | |
 | そうですね。なので、活性層から放射された後も、その影響は残り、\(z\)方向の(複素)振幅の変化は緩やかであると見なすのが合理的です。そこで、求める波動関数\(u(x,y,z)\)を次のように書くことにしましょう。 \[ u \left( x,y,z \right) = \psi \left( x,y,z \right) \mathrm{e}^{ikz} \tag{5.2.1} \] | |
 | つまり、基本的には\(z\)方向の平面波だけど、緩やかな成分\(\psi(x,y,z)\)が作用している、ってことですね。 | |
 | これを近軸近似と言ったりします。 | |
 | 近軸?? | |
 | 平面波からの変化が緩やかだ、ということは、(複素)振幅の変化はどこをとっても近軸領域と大差ない、ということですよね??だから、近軸近似なのです。さて、式5.2.1を式1.2.1に代入します。 | |
 | ステップ踏んでやった方がよさそうですね。 \[ \frac{ \partial u }{ \partial z } = \frac{ \partial \psi }{ \partial z } \mathrm{e}^{ikz} + ik \psi \mathrm{e}^{ikz} \] だから、 \[ \begin{align*} \frac{ \partial^2 u }{ \partial z^2 } &= \frac{ \partial^2 \psi }{ \partial z^2 } \mathrm{e}^{ikz} + ik \frac{ \partial \psi }{ \partial z } \mathrm{e}^{ikz} + ik \frac{ \partial \psi }{ \partial z } \mathrm{e}^{ikz} - k^2 \psi \mathrm{e}^{ikz} \\ &= \left[ \frac{ \partial^2 \psi }{ \partial z^2 } + 2ik \frac{ \partial \psi }{ \partial z } \right] \mathrm{e}^{ikz} - k^2 u \end{align*} \] そうすると、Helmholtz方程式は、 \[ \begin{align*} \frac{ \partial^2 \psi }{ \partial x^2 } \mathrm{e}^{ikz} + \frac{ \partial^2 \psi }{ \partial y^2 } \mathrm{e}^{ikz} + \left[ \frac{ \partial^2 \psi }{ \partial z^2 } + 2ik \frac{ \partial \psi }{ \partial z } \right] \mathrm{e}^{ikz} - k^2 u = - k^2 u \\ \Leftrightarrow \quad \frac{ \partial^2 \psi }{ \partial x^2 } + \frac{ \partial^2 \psi }{ \partial y^2 } + \frac{ \partial^2 \psi }{ \partial z^2 } + 2ik \frac{ \partial \psi }{ \partial z } = 0 \tag{5.2.2} \end{align*} \] になりますね。 | |
 | 更に、\(z\)方向について、 \[ \left| \frac{ \partial^2 \psi }{ \partial z^2 } \right| \ll \left| k \frac{ \partial \psi }{ \partial z } \right| \] という近似が成立するとし、式5.2.2を次のように書き直しましょう。 \[ \frac{ \partial^2 \psi }{ \partial x^2 } + \frac{ \partial^2 \psi }{ \partial y^2 } + 2ik \frac{ \partial \psi }{ \partial z } = 0 \tag{5.2.3} \] このような近似を緩慢変化包絡線近似(SVEA)と言います。 | |
 | 式が簡単になるのは、いいことです。 | |
 | さて、ここで式5.2.3を満たす\(\psi(x,y,z)\)を、複素関数\(p(z)\)、\(q(z)\)を使って、 \[ \psi \left( x,y,z \right) = A \exp \biggr\{ i \left[ p \left( z \right) + \frac{ k }{ 2 q \left( z \right) } \left( x^2 + y^2 \right) \right] \biggr\} \tag{5.2.4} \] と想定しましょう。 | |
 | え〜??それは、無理ってもんですよ〜。 | |
 | 確かに、式5.2.3を見て、その解が式5.2.4のように与えられると見抜くのは難しいと思います。が、我々はすでに解の形を知っているので、ショート・カットするために、天下り的に式5.2.4として置いてしまうことにします。 | |
 | ショート・カットって、そういうことか…。 | |
 | というわけで、式5.2.4を式5.2.3に代入します。 | |
 | これも、ステップを踏んだ方がよさそうですね。 \[ \frac{ \partial \psi }{ \partial x } = i \frac{ kx }{ q } \psi \] だから、 \[ \frac{ \partial^2 \psi }{ \partial x^2 } = i \frac{ k }{ q } \psi - \frac{ k^2 x^2 }{ q^2 } \psi \] \(y\)は\(x\)と同じ流れだから、 \[ \frac{ \partial^2 \psi }{ \partial y^2 } = i \frac{ k }{ q } \psi - \frac{ k^2 y^2 }{ q^2 } \psi \] か。それで、\(z\)は…。 \[ \frac{ \partial \psi }{ \partial z } = i \frac{ \partial p }{ \partial z } \psi - i \frac{ k }{ 2 q^2 } \frac{ \partial q }{ \partial z } \left( x^2 + y^2 \right) \psi \] そうすると、全部を式5.2.3に代入すればいいのか。 \[ \begin{align*} \biggl[ i \frac{ k }{ q } \psi &- \frac{ k^2 x^2 }{ q^2 } \psi \biggr] + \biggl[ i \frac{ k }{ q } \psi - \frac{ k^2 y^2 }{ q^2 } \psi \biggr] + 2ik \biggl[ i \frac{ \partial p }{ \partial z } \psi - i \frac{ k }{ 2 q^2 } \frac{ \partial q }{ \partial z } \left( x^2 + y^2 \right) \psi \biggr] \\ &= 2i \frac{ k }{ q } \psi - \frac{ k^2 }{ q^2 } \left( x^2 + y^2 \right) \psi - 2k \frac{ \partial p }{ \partial z } \psi + \frac{ k^2 }{ q^2 } \frac{ \partial q }{ \partial z } \left( x^2 + y^2 \right) \psi \\ &= \biggl[ 2k \left( \frac{ i }{ q } - \frac{ \partial p }{ \partial z } \right) + \frac{ k^2 }{ q^2 } \left( \frac{ \partial q }{ \partial z } - 1 \right) \left( x^2 + y^2 \right) \biggr] \psi = 0 \\ \end{align*} \] | |
 | これは、すべての\((x,y)\)で成立しないといけないので、 \[ \frac{ i }{ q } - \frac{ \partial p }{ \partial z } = 0 \tag{5.2.5} \] \[ \frac{ \partial q }{ \partial z } - 1 = 0 \tag{5.2.6} \] です。 | |
 | 積分定数を\(q_0\)とすると、式5.2.6から、 \[ q \left( z \right) = z + q_0 \tag{5.2.7} \] と求まりますね。 | |
 | 式5.2.7を式5.2.5に代入すると?? | |
 | ん〜と。 \[ \begin{align*} \frac{ \partial p }{ \partial z } = \frac{ i }{ q } = \frac{ i }{ z + q_0 } &\Leftrightarrow \quad \int dp = \int \frac{ i }{ z + q_0 } dz \\ &\Leftrightarrow \quad p(z) = i \ln \left( z + q_0 \right) + C_0 \tag{5.2.8} \end{align*} \] かな。\(C_0\)は積分定数ですけど。 | |
 | 式5.2.8は、 \[ C_0 = -i \ln q_0 \] として、 \[ \begin{align*} p(z) &= i \ln q_0 \left( \frac{ z }{ q_0 } + 1 \right) + C_0 = i \ln q_0 + i \ln \left( \frac{ z }{ q_0 } + 1 \right) -i \ln q_0 \\ &= i \ln \left( \frac{ z }{ q_0 } + 1 \right) \tag{5.2.9} \end{align*} \] と変形しておきましょう。 | |
 | 教授のやっていることに必然性を感じませんけど?? | |
 | 後々、分かってきます。更に、積分定数\(q_0\)は、 \[ q_0 = -i \frac{ k { \omega_0 }^2 }{ 2 } \equiv -i z_0 \tag{5.2.10} \] としておきます。 | |
 | 新しい変数\(\omega_0\)が登場してますけど?? | |
 | それも後々、分かってきます。 | |
 | 推理小説みたいですね…。 | |
 | もっと謎を深めましょうか。式5.2.10を式5.2.9に代入します。 \[ \begin{align*} p(z) &= i \ln \left( - \frac{ z }{ i z_0 } + 1 \right) = i \ln \left( 1 +i \frac{ z }{ z_0 } \right) \\ &= i \left[ \ln \sqrt{ 1 + \left( \frac{ z }{ z_0 } \right)^2 } + i \tan^{-1} \left( \frac{ z }{ z_0 } \right) \right] \\ &= i \ln \sqrt{ 1 + \left( \frac{ z }{ z_0 } \right)^2 } - \tan^{-1} \left( \frac{ z }{ z_0 } \right) \tag{5.2.11} \end{align*} \] | |
 | ムムム。途中で公式か何か使ってます?? | |
 | はい。 \[ \ln \left( a + ib \right) = \ln \sqrt{ a^2 + b^2 } + i \tan^{-1} \frac{ b }{ a } \] という公式を使ってます。複素平面から直ちに導かれる公式ですが、ここでは証明を省きましょう。 | |
 | \(p(z)\)と\(q(z)\)が求まったから、式5.2.4が確定しそうですけど…。 | |
 |
やってみましょう。その前に、
\[
\begin{align*}
\frac{ k }{ 2 q } &= \frac{ k }{ 2 \left( z + q_0 \right) } = \frac{ k }{ 2 \left( z - i z_0 \right) } = \frac{ k \left( z + i z_0 \right) }{ 2 \left( z^2 + {z_0}^2 \right) } \\
&= \frac{ k }{ 2 z \left[ 1 + \left( \cfrac{z_0}{z} \right)^2 \right] } + i \frac{ k }{ 2 z_0 \left[ 1 + \left( \cfrac{z}{z_0} \right)^2 \right] }
\end{align*}
\]
ここで、
\[
R \left( z \right) \equiv z \left[ 1 + \left( \frac{z_0}{z} \right)^2 \right] \tag{5.2.12}
\]
\[
\omega^2 \left( z \right) \equiv \frac{ 2 z_0 }{ k } \left[ 1 + \left( \frac{z}{z_0} \right)^2 \right] = {\omega_0}^2 \left[ 1 + \left( \frac{z}{z_0} \right)^2 \right] \tag{5.2.13}
\]
とし、
\[
\frac{ k }{ 2 q } = \frac{ k }{ 2 R \left( z \right) } + \frac{ i }{ \omega^2 \left( z \right) } \tag{5.2.14}
\]
という準備をしておいて…。
\[
\begin{align*}
\psi &= A \exp \Biggr\{ i \left[ i \ln \sqrt{ 1 + \left( \frac{ z }{ z_0 } \right)^2 } - \tan^{-1} \left( \frac{ z }{ z_0 } \right) + \left( \frac{ k }{ 2 R } + \frac{ i }{ \omega^2 } \right) \left( x^2 + y^2 \right) \right] \Biggr\} \\
&= A \exp \left[ - \ln \sqrt{ 1 + \left( \frac{ z }{ z_0 } \right)^2 } \right] \exp \left[ -i \tan^{-1} \left( \frac{ z }{ z_0 } \right) + i \left( \frac{ k }{ 2 R } + \frac{ i }{ \omega^2 } \right) \left( x^2 + y^2 \right) \right] \\
&= \frac{ A }{ \sqrt{ 1 + \left( \cfrac{ z }{ z_0 } \right)^2 } } \exp \left[ -i \tan^{-1} \left( \frac{ z }{ z_0 } \right) + \left( i \frac{ k }{ 2 R } - \frac{ 1 }{ \omega^2 } \right) \left( x^2 + y^2 \right) \right] \\
\end{align*}
\]
\[
\phantom{\psi} = A \frac{ \omega_0 }{ \omega } \exp \left[ -i \tan^{-1} \left( \frac{ z }{ z_0 } \right) + \left( i \frac{ k }{ 2 R } - \frac{ 1 }{ \omega^2 } \right) \left( x^2 + y^2 \right) \right] \tag{5.2.15}
\]
更に、
\[
\phi \left( z \right) \equiv \tan^{-1} \left( \frac{ z }{ z_0 } \right) \tag{5.2.16}
\]
としたうえで、式5.2.15と式5.2.16を式5.2.1に代入すると、
\[
\begin{align*}
u \left( x,y,z \right) = A \frac{ \omega_0 }{ \omega \left( z \right) } \exp \left[ -i \phi \left( z \right) + \left[ i \frac{ k }{ 2 R \left( z \right) } - \frac{ 1 }{ \omega^2 \left( z \right) } \right] \left( x^2 + y^2 \right) \right] \mathrm{e}^{ikz} \\
\quad \quad \quad = A \frac{ \omega_0 }{ \omega \left( z \right) } \exp \biggr\{ i \Big[kz - \phi \left( z \right) \Big] + \left[ i \frac{ k }{ 2 R \left( z \right) } - \frac{ 1 }{ \omega^2 \left( z \right) } \right] \left( x^2 + y^2 \right) \biggr\} \tag{5.2.17}
\end{align*}
\]
という最終結果が得られます。式5.2.16は、特にGouy位相と呼んだりもしますね。
 Louis Georges Gouy(1854〜1926) |
|
 | よくよく見てみると、式5.2.17に時間のパラメータがないんですけど?? | |
 | ビームの伝搬の様子を議論するときは、空間的な広がり方だけに興味があるので、時間の項は省略されるのが普通です。 | |
 | それにしても、数式を捏ね繰りまわすだけ捏ね繰りまわして、式5.2.17の意味は分からないままでは?? | |
 | そうですね。式5.2.17の意味は、次回、調べていくことにしましょう。 |
| 前頁へ | 戻る | 次頁へ |