 | さて、波動関数が式5.2.17のように求まったので、強度\(I\left(z\right)\)を求めてみましょう。 | |
 | ん〜と。 \[ I \left( x,y,z \right) = \bigg| u \left( x,y,z \right) \bigg|^2 = A^2 \left[ \frac{ \omega_0 }{ \omega \left( z \right) } \right]^2 \exp \left[ - \frac{ 2 }{ \omega^2 \left( z \right) } \left( x^2 + y^2 \right) \right] \tag{5.2.18} \] ですね。 | |
 | そうすると、ある\(z\)を決めたときの\(xy\)平面内の強度分布が議論できますね。 | |
 | そうか。その強度分布がGauss関数になっているから、Gaussainビームって言うわけですね。 | |
 | 式5.2.18は、\(x\)と\(y\)の係数が同じなので、強度のピークを中心とした同心円の強度分布を示していますが、 \[ \exp \left[ -2 \left( \frac{ x^2 }{ {\omega_x}^2 \left( z \right) } + \frac{ y^2 }{ {\omega_y}^2 \left( z \right) } \right) \right] \] とすると、楕円の強度分布になって、より汎用性が広がります。いずれにせよ、この\(\omega\left(z\right)\)をビーム・スポット・サイズと呼ぶことにします。ビーム・スポット・サイズにおける強度はどうなりますか?? | |
 | それは\(x^2+y^2\)を\(\omega^2\)に置き換えればいいから簡単ですね。 \[ I = A^2 \left[ \frac{ \omega_0 }{ \omega \left( z \right) } \right]^2 \frac{ 1 }{ \mathrm{e}^2 } \tag{5.2.19} \] | |
 |
つまり、ビーム・スポット・サイズとは、ピーク強度の\(\cfrac{1}{\mathrm{e}^2}\)となる拡がり(=半径)である、と定義することができます。
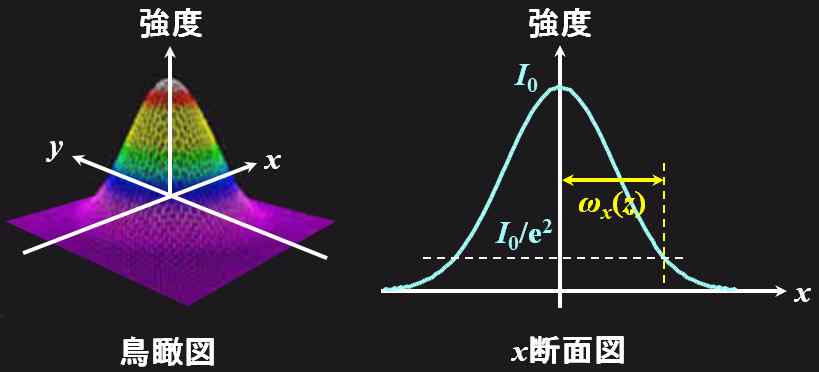 図5.2.8 強度分布とビーム・スポット・サイズ |
|
 | なるほど。これが、レーザ・ビームにおける\(\omega\)の正体なわけですね。 | |
 |
この\(\omega\)は、式5.2.13を見ると、\(z=0\)のとき最小値\(\omega_0\)となる、\(\left|z\right|\)の増加関数になっています。
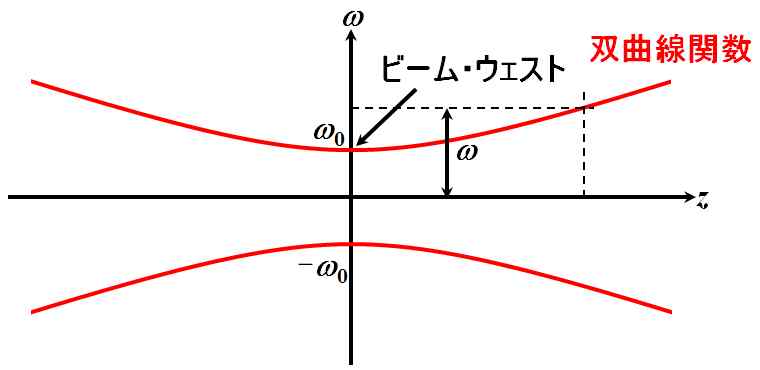 図5.2.9 Gaussianビーム 特に、\(\omega_0\)をビーム・ウェストと言います。 |
|
 | キュッと縊れているからか。なかなか乙なネーミングですね。 | |
 |
式5.2.13を少し変形してみましょう。
\[
\frac{ \omega^2 }{ {\omega_0}^2 } - \frac{z^2}{{z_0}^2} = 1
\]
これは、典型的な双曲線ですから、この関数は、
\[
\omega = \pm \frac{ \omega_0 }{ z_0 } z
\]
という漸近線に近づいていきます。更に、
\[
\theta = 2 \tan^{-1} \frac{ \omega_0 }{ z_0 } \approx 2 \frac{ \omega_0 }{ z_0 } = \frac{ 4 }{ k \omega_0 } = \frac{ 2 \lambda }{ \pi \omega_0 } \tag{5.2.20}
\]
をビーム拡がり角と言います。途中で、式5.2.10と式1.1.9を使いました。更に、式5.2.20を、
\[
\omega_0 = \frac{ 2 \lambda }{ \pi \theta } \tag{5.2.21}
\]
と変形すると、\(\theta\)は\(0\)〜\(\pi\)しか取り得ないので、\(\omega_0\)はどんなに頑張っても\(0\)になることはありません。高々、\(\lambda\)程度です。
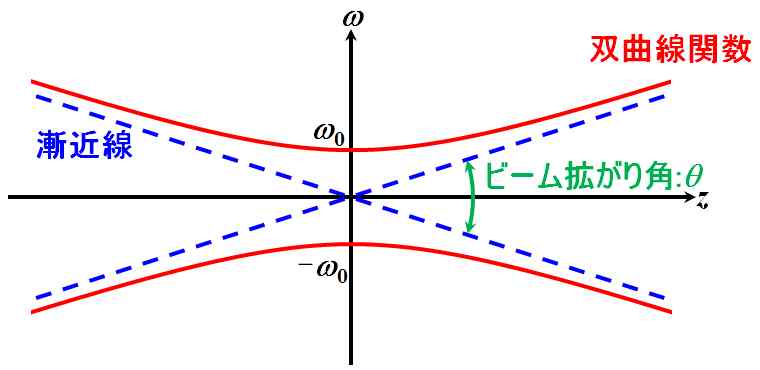 図5.2.10 ビーム拡がり角 |
|
 | それって、回折の効果なんですか?? | |
 | そうですね。そう捉えて構いません。 | |
 | 次は、\(R\left(z\right)\)ですね。 | |
 | これは、等位相面を表していると考えられます。 | |
 | 等位相面って言うことは、要するに波面ってことですね。波数\(k\)の係数になっているからか…。 | |
 | 式5.2.12と式5.2.17を見ながら、まず\(z\ll z_0\)の領域における波面がどうなっているか考えてみましょう。 | |
 | 式5.2.12から、\(z \rightarrow 0\)のとき、 \[ R \left( z \right) = z \left[ 1 + \left( \frac{z_0}{z} \right)^2 \right] = z + \frac{ {z_0}^2 }{ z } \rightarrow \infty \] なので、式5.2.17の波数の成分は、 \[ kz + \frac{ k }{ 2 R \left( z \right) } \left( x^2 + y^2 \right) \rightarrow kz \] かな?? | |
 | ということは?? | |
 |
平面波ですね。
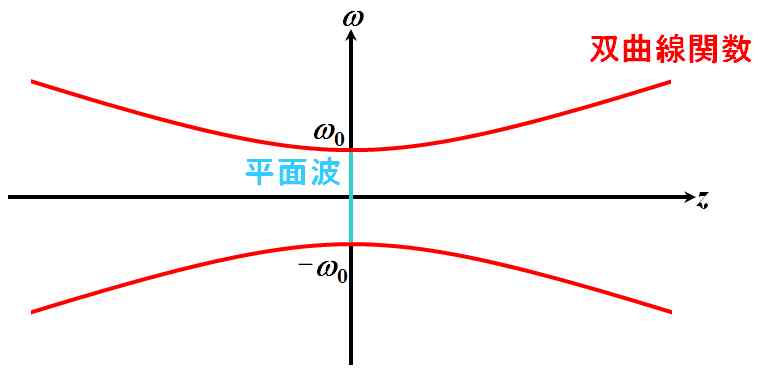 図5.2.11 中心付近の波面 |
|
 | では、\(z \gg z_0\)の領域だと、どうでしょう?? | |
 | 式5.2.12から、\(z\)が大きくなっていくと、 \[ R \left( z \right) = z \left[ 1 + \left( \frac{z_0}{z} \right)^2 \right] = z + \frac{ {z_0}^2 }{ z } \rightarrow z \] なので、式5.2.17の波数の成分は、 \[ kz + \frac{ k }{ 2 R \left( z \right) } \left( x^2 + y^2 \right) \rightarrow kz + \frac{ k }{ 2z } \left( x^2 + y^2 \right) = k \left[ z + \frac{ x^2 + y^2 }{ 2z } \right] \] だけど、その先が続きそうにないですね。 | |
 | そこで、この議論は近軸領域であるという考えに則って、\(z \gg \{x,y\}\)とすれば、 \[ R \left( z \right) \approx R \left( x,y,z \right) = \sqrt{ x^2 + y^2 + z^2 } = z \sqrt{ 1 + \frac{ x^2 + y^2 }{ z^2 }} \approx z + \frac{ x^2 + y^2 }{ 2z } \] と近似できるので、 \[ k \left[ z + \frac{ x^2 + y^2 }{ 2z } \right] \rightarrow kR \left( x,y,z \right) \] と変形できますよね?? | |
 |
だから、球面波だ、ってことですね。ここまでくると、近似に何か執念を感じますね。
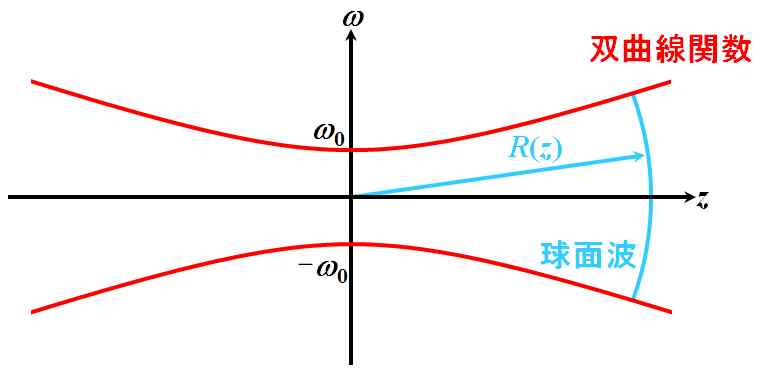 図5.2.12 遠方の波面 |
|
 | \(z\)が\(\infty\)になれば、結局\(R\left(z\right)\)も\(\infty\)になるんですが、それは\(z=0\)における平面波とは異なり、球面波の曲率が緩やかに\(0\)に近づいた結果による平面波だと考えることができます。 | |
 | ん??\(z=0\)でも\(R=\infty\)で、\(z=\infty\)でも\(R=\infty\)だとすると、\(R\)はどこかで最小値をとりそうな気がしますね。 | |
 | 鋭い着眼点です。どこになりますか?? | |
 |
それは、式5.2.12を\(z\)で微分して、
\[
\frac{ dR }{ dz } = 1 - \frac{ {z_0}^2 }{ z^2 }
\]
これが\(0\)になればいいから、
\[
1 - \frac{ {z_0}^2 }{ z^2 } = 0 \Leftrightarrow \left| z \right| = z_0
\]
ですね。
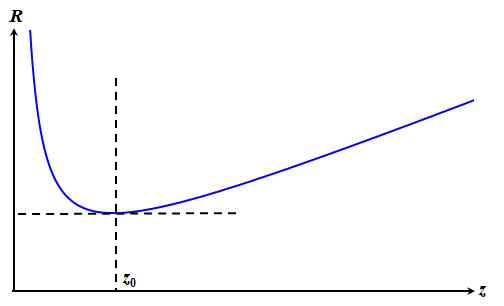 図5.2.13 \(R\)の変化 |
|
 |
つまり、\(z_0\)というのは、波面の曲率半径が最小値をとる\(z\)の位置であると定義することができそうです。この\(z_0\)を共焦点パラメータとかRayleigh長と言ったりします。更に、\(-z_0\)〜\(z_0\)に挟まれた\(z\)の範囲をコンフォーカル長と言います。これは、カメラレンズの被写界深度に対応するものになります。
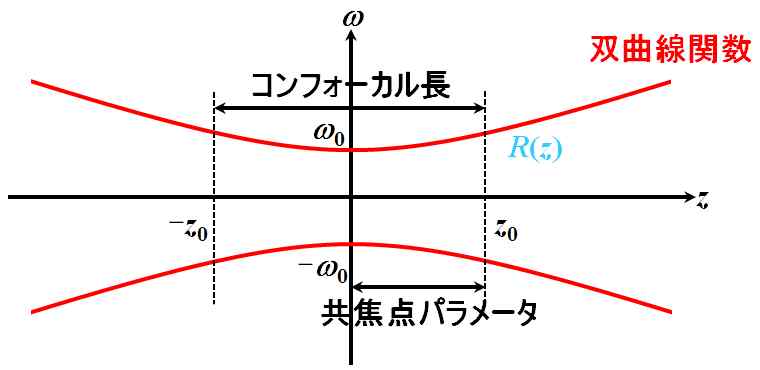 図5.2.14 \(z_0\)の正体 |
|
 | 教授。被写界深度って、人間の視力では判別できないボケの許容範囲ですよね??ということは、コンフォーカル長って、どういう意味になるんですか?? | |
 | つまり、ビーム・スポット・サイズがビーム・ウェストと同じだと見なせる範囲、ってことですよ。 | |
 | え〜。だって、\(z=z_0\)のとき、式5.2.13から、\(\omega^2\)って\(2{\omega_0}^2\)ですよ??面積、倍ですよ??絶対、同じじゃないですよ〜。 | |
 | あくまで便宜的に、ってことです。実用的に、そのように運用していいかどうかは別の議論になります。ただ、「ビーム・スポット・サイズの許容範囲」を議論するときに、土俵を揃えておかないと、議論にならないでしょう??だから、何らかの定義をしておくことは、非常に有益なんです。 | |
 | そういうことか。 | |
 | 以上で、Gaussianビームの概要は押さえられたと思います。尚、ここでビーム・スポット・サイズについて注意をしておきます。 | |
 | ん??注意?? | |
 | ビーム・スポット・サイズの定義は何だったでしょう?? | |
 | ピーク強度の\(\cfrac{1}{\mathrm{e}^2}\)となる拡がり(=半径)ですね。 | |
 | ということは、ピーク強度そのものは考慮の外になります。つまり、ビーム・スポット・サイズはピーク強度を正規化していることになります。 | |
 | 別に、いいじゃないですか。 | |
 | そうですか??例えば、LSUから放射したビームで感光体を露光させた場合、そこで生じたドットのサイズは、必ずしもビーム・スポット・サイズと同じではありません。 | |
 |
あ!!そうか。極端な話、露光できるだけの強度がなければ、ドットは生成されないけど、ビーム・スポット・サイズは限りなく強度を小さくしても\(\cfrac{1}{\mathrm{e}^2}\)の半径として計算できちゃいますもんね。
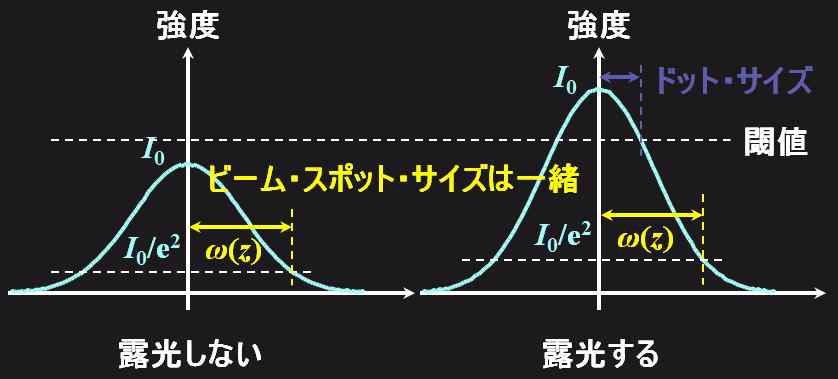 図5.2.15 ビーム・スポット・サイズとドット・サイズ |
|
 | そういうことです。厳密なことを言うと、露光できるかどうかはエネルギーで議論すべきなので、小さな光量でも、ゆっくり時間をかけてやれば露光エネルギーの閾値を超えることは可能です。しかし、そうなると、1分間に印字できる枚数が減ってしまいます。よって、このLSUは1分間に何枚印字するのか、感光体の露光エネルギーの閾値はいくらか、という観点から、感光体を照射する光量の閾値に換算し、LDから感光体までに配備される光学系の光利用効率を加味して、LDに必要とされる光量を決めることになります。いずれにせよ、プロセスの専門家と議論するときに、ドット・サイズとビーム・スポット・サイズを混同してしまうと、いらぬ誤解を生じたまま話が進んでしまう危険があることに注意しないといけません。 | |
 | あくまで、ビーム・スポット・サイズは理論上、便宜的に定義されたものだってことですね。 | |
 | はい。ビーム・スポット・サイズからドット・サイズに変換することは可能ですが、そこには強度なり光量なりの情報が必要で、単純に何倍すればいい、というような理屈は通りません。ちなみに、このビームの光量を\(P\)として、これを求めてみましょう。 | |
 | 式5.2.18を積分すればいいかな。 \[ P = A^2 \left[ \frac{ \omega_0 }{ \omega \left( z \right) } \right]^2 \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \exp \left[ - \frac{ 2 }{ \omega^2 \left( z \right) } \left( x^2 + y^2 \right) \right] dx dy \] Gauss積分の公式を使うと、 \[ \int_{- \infty}^{\infty} \exp \left[ - \frac{ 2 }{ \omega^2 \left( z \right) } x^2 \right] dx = \omega \left( z \right) \sqrt{ \frac{\pi}{2} } \] だから、結局、 \[ P = A^2 \left[ \frac{ \omega_0 }{ \omega \left( z \right) } \right]^2 \omega^2 \left( z \right) \frac{\pi}{2} = A^2 \frac{ \pi {\omega_0}^2 }{ 2 } \tag{5.2.22} \] ですね。 | |
 | 式5.2.22を使うと、式5.2.18は次のように変形できます。 \[ \begin{align*} I \left( x,y,z \right) &= A^2 \frac{ \pi {\omega_0}^2 }{ 2 } \frac{ 2 }{ \pi \omega^2 \left( z \right)} \exp \left[ - \frac{ 2 }{ \omega^2 \left( z \right) } \left( x^2 + y^2 \right) \right] \\ &= \frac{ 2P }{ \pi \omega^2 \left( z \right)} \exp \left[ - \frac{ 2 }{ \omega^2 \left( z \right) } \left( x^2 + y^2 \right) \right] \tag{5.2.23} \end{align*} \] いずれせよ、ビーム・スポット・サイズを議論する場合には、光量の部分が正規化されてしまう点に注意しないといけません。 |
〜レーザ・ビーム品質〜
 | 教授。Gaussianビームって現実的に得ることはできるんですか?? | |
 | どういうことでしょう?? | |
 | だって、たいていの理論は「理想状態」が前提ですよね??理想と現実は違う、ってよく言いますよ。 | |
 | そうですね。厳密な意味でのGaussianビームを現実に得ることは難しいと考えていいでしょう。しかし、NFP(ニア・フィールド・パタン)がGauss分布に近似できるのであれば、実際上Gaussianビームとして取り扱っても構わないとは言えます。 | |
 | NFP?? | |
 | レーザから放射されたビームの、放射直後の強度分布です。横モードとも言いますね。NFPは、LDが経年劣化を起こすと高次モードが出現してきますが、レーザ共振器の構造によっても大幅に変わります。 | |
 | でも、今までの議論では、Gaussianビーム以外の解は出てきませんよ?? | |
 | それは、予想される解を式5.2.4のように置いたからですね。高次モードを議論する場合は、\(\psi_{nm} \left(x,y,z \right) = \psi_n \left( x,z \right) \psi_m \left(y,z \right)\)と置いて、計算していくことになります。\(n\)とか\(m\)は高次モードを表す次数です。 | |
 | Gaussianビームは、\(\left(0,0\right)\)モードってこと?? | |
 |
そうです。高次モードは極座標系で解くとLaguerre-Gauss(LG)型(論文)、
 Edmond Nicolas Laguerre(1834〜1886) Descartes座標系で解くとHermite-Gauss(HG)型として記述されます。  Charles Hermite(1822〜1901) |
|
 | 2種類だけ?? | |
 | いえ、他にもありますが、代表的なものとして、この2つを押さえておけば充分です。 | |
 | 教授。このHermiteって人、凄く怖そうですね〜。 | |
 | フランスの数学者ですが、この人は生まれつき右足が悪く、天才のわりに、なかなかの苦労人だったようですね。ただ、講義が頗る上手く、たくさんの弟子を輩出しています(ちなみに、Laguerreも優れた教育者として有名)。業績も多く、例えばNapier数\(\mathrm{e}\)が超越数であることを証明したり(論文)、5次方程式の解法を発見したり(論文)しています。 | |
 |
5次方程式??それは嘘ですよ〜。だって、5次以上の方程式には解の公式が存在しないことを、Abelっていう数学者が証明してる(論文)じゃないですか。
 Niels Henrik Abel(1802〜1829) |
|
 | それは「代数的解法では」という条件つきです。Hermiteは、その枠を取っ払って、楕円関数を使って解決したのです。 | |
 | 高次モードのNFPって、どういう感じになっているんですか?? | |
 |
それぞれは、図5.2.16のように見えます。
 図5.2.16 いろいろな横モード |
|
 | 図の下にある数字のセットがモードの次数ですね?? | |
 | そうです。 | |
 | 数式で表現したら、いかにも複雑そうですね。 | |
 | はい。ですので、ここではLG型もHG型も扱いません。それよりも、Gaussianビームとは名ばかりの、実際は強度分布がGauss分布でないレーザ・ビームの品質について考えていくことにしましょう。特に、ハイパワーのレーザとか、イオン・ビームなどは、Gauss分布からのズレが大きくなっていきます。 | |
 | Gauss分布ではない、ということを数値的に表現できないといけませんね。 | |
 |
これについては、1990年頃にSiegmanの提案した(論文)\(M^2\)がよく利用されていると思います。
 Anthony Siegman(1931〜2011) |
|
 | \(M^2\)?? | |
 | M-Squareと言います。これは、まずビーム・パラメータ積(\({\rm BBP}\))を、 \[ {\rm BBP} = \theta \omega_0 \tag{5.2.24} \] のように定義し、理想的な\({\rm BBP}^{\left({\rm ideal}\right)}\)と実際の\({\rm BBP}^{\left({\rm real}\right)}\)の比として定義されます。 | |
 | \(\theta\)はビーム拡がり角で、\(\omega_0\)はビーム・ウェストですね。 | |
 | はい。理想的な\({\rm BBP}^{\left({\rm ideal}\right)}\)は、式5.2.20から、 \[ {\rm BBP}^{\left( {\rm ideal} \right)} = \frac{2 \lambda }{ \pi {\omega_0}^{\left( {\rm ideal} \right)}} {\omega_0}^{\left( {\rm ideal} \right)} = \frac{2 \lambda }{ \pi } \tag{5.2.25} \] なので、\(M^2\)は、 \[ M^2 = \frac{{\rm BBP}^{\left( {\rm real} \right)}}{{\rm BBP}^{\left( {\rm ideal} \right)}} = {\theta}^{\left( {\rm real} \right)} {\omega_0}^{\left( {\rm real} \right)} \div \frac{ 2 \lambda}{ \pi } = \frac{ \pi }{ 2 \lambda } {\theta}^{\left( {\rm real} \right)} {\omega_0}^{\left( {\rm real} \right)} \tag{5.2.26} \] となります。式5.2.26の\({\theta}^{\left( {\rm real} \right)}\)と\({\omega_0}^{\left( {\rm real} \right)}\)は実測値でなければいけません。 | |
 | ビーム・ウェストは理想からズレていくと太っていくから、\(M^2\)は\(1\)よりも大きくなるわけですね。 | |
 | 大きくなればなるほど、レーザ・ビームの品質は悪くなります。一般的なLDやHe-Neレーザなどは、\(1\)に近いですが、ハイパワーになってくるとマルチ・モードの傾向が強くなるので、\(3\)くらいになることはザラですね。また、Gaussianビームをレンズで集光させた場合、レンズの収差の影響で\(M^2\)が大きくなるケースもあります。 | |
 | \(M^2\)が分かったとして、そのときのビーム・ウェストは、\(M\)倍されると考えればいいんですか?? \[ {\omega_0}^{\left( {\rm real} \right)} = M{\omega_0}^{\left( {\rm ideal} \right)} \tag{5.2.27} \] | |
 | そうです。よって、式5.2.13は、 \[ {\omega}^{\left( {\rm real} \right)} \left( z \right) =M {\omega}^{\left( {\rm ideal} \right)} \left( z \right) = M {\omega_0}^{\left( {\rm ideal} \right)} \sqrt{ 1 + \left( \frac{z}{{z_0}^{\left( {\rm ideal} \right)}} \right)^2 } \tag{5.2.28} \] のように修正されます。 | |
 | \({\theta}^{\left( {\rm real} \right)}\)は?? | |
 | やっぱり、\(M\)倍ですね。 \[ {\theta}^{\left( {\rm real} \right)} =M {\theta}^{\left( {\rm ideal} \right)} = M \frac{2 \lambda}{\pi {\omega_0}^{\left( {\rm ideal} \right)}} = M \cfrac{2 \lambda}{\pi \cfrac{{\omega_0}^{\left( {\rm real} \right)}}{M}} = M^2 \frac{2 \lambda}{\pi {\omega_0}^{\left( {\rm real} \right)}} \tag{5.2.29} \] 途中で、式5.2.20と式5.2.27を使いました。 | |
 | 式5.2.29から、実測でのビーム拡がり角とビーム・ウェストが分かれば、\(M^2\)が求まるわけですね。 | |
 | いえ。それだと2つのパラメータについて測定しないといけないので面倒です。その代わりに、式5.2.28を少し変形して、ビーム・スポット・サイズを測定するだけで\(M^2\)が求まるように工夫します。 | |
 | そうか。\(\theta^{\left({\rm real}\right)}\)の測定も容易じゃなそうですしね。 | |
 | まず、式5.2.28はビーム・ウェストが原点にあることが前提になってますが、測定するときは、その前提が崩れるので、ビーム・ウェストの\(z\)座標を\(z_{\rm BW}\)としておきましょう。 \[ \begin{align*} \{ {\omega}^{\left( {\rm real} \right)} \left( z \right) \}^2 &= \left[ M {\omega_0}^{\left( {\rm ideal} \right)} \right]^2 + \left( \frac{M {\omega_0}^{\left( {\rm ideal} \right)}}{{z_0}^{\left( {\rm ideal} \right)}} \right)^2 \left( z - z_{\rm BW} \right)^2 \\ &= \{ {\omega_0}^{\left( {\rm real} \right)} \}^2 + \left[ \frac{2 {\omega_0}^{\left( {\rm real} \right)}}{k \{ {\omega_0}^{\left( {\rm ideal} \right)} \}^2 } \right]^2 \left( z - z_{\rm BW} \right)^2 \\ &= \{ {\omega_0}^{\left( {\rm real} \right)} \}^2 + \left[ \frac{2 {\omega_0}^{\left( {\rm real} \right)} }{k \left( {\omega_0}^{\left( {\rm real} \right)} /M \right)^2} \right]^2 \left( z - z_{\rm BW} \right)^2 \\ &= \{ {\omega_0}^{\left( {\rm real} \right)} \}^2 + \left[ \frac{2M^2 {\omega_0}^{\left( {\rm real} \right)} }{k \{ {\omega_0}^{\left( {\rm real} \right)} \}^2} \right]^2 \left( z - z_{\rm BW} \right)^2 \\ &= \{ {\omega_0}^{\left( {\rm real} \right)} \}^2 + M^4 \left( \frac{2}{k {\omega_0}^{\left( {\rm real} \right)} } \right)^2 \left( z - z_{\rm BW} \right)^2 \tag{5.2.30} \end{align*} \] こうしておけば、ビーム・スポット・サイズの測定結果から、\(M^2\)が求まります。 | |
 | でも、ここでのレーザ・ビームの強度分布はGauss分布じゃないから、ビーム・スポット・サイズなんて求めようがないんじゃないですか?? | |
 | そうですね。なので、\(M^2\)を実験的に求めるためには、正しい手順を踏まないといけません。現在、この手順はISO11146で標準化されています。 | |
 | ビーム・スポット・サイズを定義し直さないと、ですね。 | |
 |
その定義は、Gauss分布のときの\(\omega\)が、ピーク強度の\(\cfrac{1}{\mathrm{e}^2}\)と一致するようなものでなければなりません。が、これは数学的に考察すると、それほど難しい話ではなく、Gauss分布のとき、強度分布の標準偏差を\(\sigma\)とすると、\(x=y=\pm 2 \sigma\)においてピーク強度の\(\cfrac{1}{\mathrm{e}^2}\)になることから、Gauss分布でない場合も、強度分布の標準偏差を求めて、\(2\sigma\)をビーム・スポット・サイズと再定義してやると見通しがよさそうです。
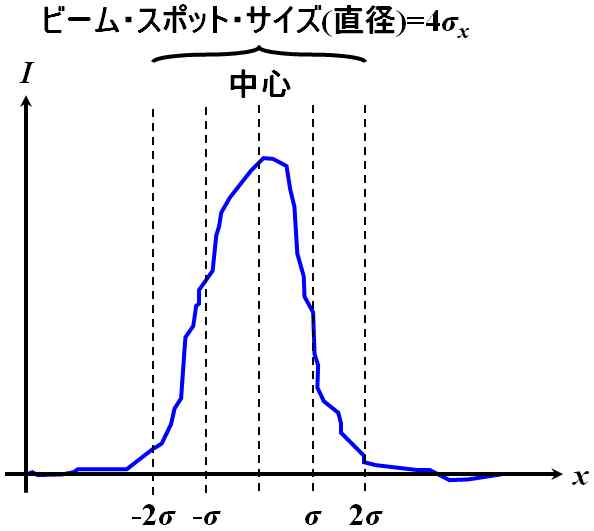 図5.2.17 Gauss分布でない強度分布 これを直径に直した\(4\sigma\)は二次モーメント幅とか\(D4 \sigma\)幅と呼ばれます。 \[ 2 {\omega_x}^{\left( {\rm real} \right)} = 4\sigma_x = 4 \sqrt{\frac{\displaystyle \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} \left( x-\mu_x \right)^2 I \left( x,y \right) dxdy}{\displaystyle \int^{\infty}_{-\infty} \int^{\infty}_{-\infty}I \left( x,y \right) dxdy}} \tag{5.2.31} \] ここで、\(\mu_x\)は期待値です。 \[ \mu_x = \frac{\displaystyle \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} x I \left( x,y \right) dxdy}{\displaystyle \int^{\infty}_{-\infty} \int^{\infty}_{-\infty}I \left( x,y \right) dxdy} \tag{5.2.32} \] |
|
 | これは\(x\)方向についての式だから、\(y\)方向は、\(x\)と\(y\)をひっくり返せばいいわけですね。 | |
 | そのとおりです。 | |
 | でも、この数式、ピンと来ないですね…。 | |
 |
直感的には、強度分布を\(x\)軸に沿って細い短冊に切ってやり、
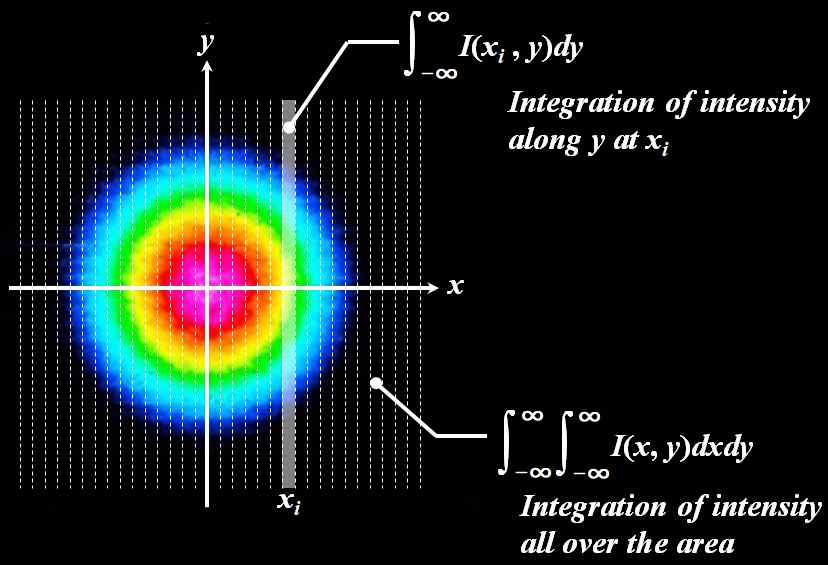 図5.2.18 \(x\)方向の期待値と標準偏差の求め方(色は強度を示し、赤は高く、青は低い) \(i\)番目の短冊\(x_i\)について「\(y\)方向に積分した値を分布全体の積分値で割ったもの」を確率密度関数\(f\left(x_i\right)\)と見なせば、 \[ f \left( x_i \right) = \frac{\displaystyle \int^{\infty}_{-\infty} I \left( x_i,y \right) dy}{\displaystyle \int^{\infty}_{-\infty} \int^{\infty}_{-\infty}I \left( x,y \right) dxdy} \tag{5.2.33} \] 通常の確率論で出てくる期待値と分散(標準偏差)の公式そのままであることが理解できるはずです。 \[ \mu_x = \int^{\infty}_{-\infty} x f \left( x \right) dx \tag{5.2.34} \] \[ {\sigma_x}^2 = \int^{\infty}_{-\infty} \left( x-\mu_x \right)^2 f \left( x \right) dx \tag{5.2.35} \] |
|
 | そういうことか。これで、ビーム・スポット・サイズは決まったけど…。 | |
 |
あとは、\(z\)方向に測定器を移動させて、\({\omega_x}^{\left( {\rm real} \right)}\)と\({\omega_y}^{\left( {\rm real} \right)}\)を求め、それを式5.2.30でフィッティングするだけです。
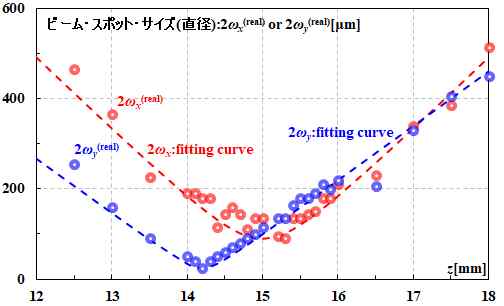 図5.2.19 \(M^2\)の測定 尚、ISO11146では、測定点は10以上、測定する個所も指示されています。 |
|
 | そういうことか。 | |
 | 但し、\(M^2\)は万能ではありません。 | |
 | \(M^2\)でレーザ・ビーム品質を判断していいかどうか、その見極めが必要になるわけですね…。 | |
 | 尤も、使う側からすれば、メーカーが\(M^2\)を提示している場合には、それを利用すれば事足りるので、あまり心配する必要はないと思います。 |
| 前頁へ | 戻る | 次頁へ |