 | 教授。Gaussianビームはビーム・ウェストから広がる一方だから、実用的にはレンズで絞らないとダメですね。 | |
 | そうです。そこで、次はその取り扱いについて見ていくことにします。幾何光学では、よく光線追跡を行いますが、その1つの定式化として式4.5.19を見ましたね?? | |
 | Snellの法則を外積に拡張した式ですね。 | |
 | 実は、もう1つ別の考え方があります。 | |
 | へぇ。 | |
 | 光線追跡というのは、結局、たくさんの光学面が配列されていて、ある一つの光学面に入射する光線の位置\(x\)と角度\(\theta\)が、その次の光学面において、どのように変換されるかというふうに考えることもできます。 | |
 | なるほど。 | |
 | この考え方を採用したときに最適な数学の道具があります。 | |
 | あ〜、行列計算ですね。 | |
 | はい。この行列を光線行列とかABCD行列と言ったりします。 \[ \left( \begin{array}{cc} x_2 \\ \theta_2 \end{array} \right) = \left( \begin{array}{cc} A & B\\ C & D \end{array} \right) \left( \begin{array}{cc} x_1 \\ \theta_1 \end{array} \right) = \left( \begin{array}{cc} A x_1 + B \theta_1 \\ C x_1 + D \theta_1 \end{array} \right) \tag{5.2.36} \] | |
 | でも、それだと回転対称な光学面しか適用できなくないですか?? | |
 |
そうですね。光線行列のテクニックは、基本的に光線がどこまでも1つの平面内を伝搬するときに有効なものになります。以下の議論はKogelnikの論文(論文)に基づいて展開していきますが、2次元に限定されている議論でも、結果は非常に示唆に富んだものになっています。
 Herwig Kogelnik(1932〜) |
|
 | 以前やったJones行列だと、光学素子によって行列の形が決まってましたね。 | |
 | ABCD行列も同じです。代表的なものをいくつか示しておきましょう。まず、距離\(d\)だけ離れた2つの光学面を伝搬する場合は、 \[ \left( \begin{array}{cc} A & B\\ C & D \end{array} \right) = \left( \begin{array}{cc} 1 & d\\ 0 & 1 \end{array} \right) \tag{5.2.37} \] また、2つの光学面が焦点距離\(f\)の薄肉レンズ(凸レンズ)の場合は、 \[ \left( \begin{array}{cc} A & B\\ C & D \end{array} \right) = \left( \begin{array}{cc} 1 & 0\\ -\cfrac{1}{f} & 1 \end{array} \right) \tag{5.2.38} \] と書けます。他にもいろいろありますが、この辺は調べればすぐに分かりますね。 | |
 | Jones行列は覚えるしかない、ってことでしたけど?? | |
 |
ABCD行列は、旧来の計算と辻褄が合うように、行列の成分を決定すればいいので、求めようと思えば求められますね。例えば、式5.2.37の場合、面1における位置と角度を\(\left(x_1,\theta_1\right)\)、面2における位置と角度を\(\left(x_2,\theta_2\right)\)とすると、
\[
\left(
\begin{array}{cc}
x_2 \\
\theta_2
\end{array}
\right)
=
\left(
\begin{array}{cc}
1 & d\\
0 & 1
\end{array}
\right)
\left(
\begin{array}{cc}
x_1 \\
\theta_1
\end{array}
\right)
=
\left(
\begin{array}{cc}
x_1 + d \theta_1 \\
\theta_1
\end{array}
\right)
\]
ですが、これは図5.2.20から明らかです。
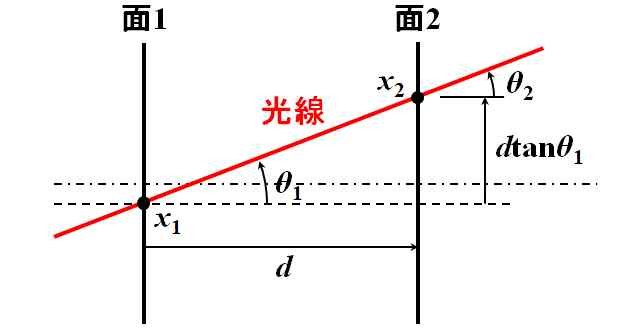 図5.2.20 自由空間の伝搬 |
|
 | \(\theta_1\)は小さいから、 \[ x_2 = x_1 + d \tan \theta_1 \approx x_1 + d \theta_1 \tag{5.2.39} \] ってことか。 | |
 |
また、式5.2.38の場合、
\[
\left(
\begin{array}{cc}
x_2 \\
\theta_2
\end{array}
\right)
=
\left(
\begin{array}{cc}
1 & 0\\
-\cfrac{1}{f} & 1
\end{array}
\right)
\left(
\begin{array}{cc}
x_1 \\
\theta_1
\end{array}
\right)
=
\left(
\begin{array}{cc}
x_1 \\
-\cfrac{x_1}{f} + \theta_1
\end{array}
\right)
\]
ですが、薄肉レンズは入射面の位置情報が、すべて出射面にそのまま転写されますし、焦点面において、
\[
\begin{align*}
f \tan \theta_1 &= x_2 + f \tan \theta_2 \quad \Leftrightarrow \quad f \theta_1 = x_2 + f \theta_2 \\
&\Leftrightarrow \quad f \theta_2 = -x_2 + f \theta_1 \quad \Leftrightarrow \quad \theta_2 = -\frac{x_2}{f} + \theta_1 = -\frac{x_1}{f} + \theta_1 \tag{5.2.40}
\end{align*}
\]
が成立するので、与えられた行列は正しいことが分かります。
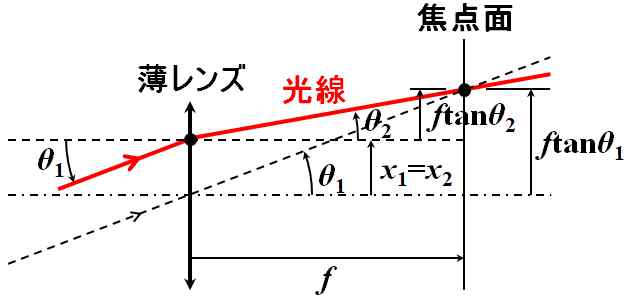 図5.2.21 薄肉レンズ |
|
 | なるほど。で、このABCD行列が何だと言うんですか?? | |
 | ABCD行列を使うと、Gaussianビームの伝搬を綺麗に表現することができるんです。 | |
 | 幾何光学の解析ツールなのに?? | |
 | 不思議でしょう?? | |
 | 俄かには信じがたいですね。だって、行列を作用させるベクトルの部分って位置と角度ですけど、Guassianビームだと、対応しそうなパラメータがなさそうですし。 | |
 | それは追って明らかになります。その準備として、式5.2.39を\(\theta_1\)で割ります。 \[ \frac{ x_2 }{ \theta_1 } = \frac{ x_1 }{ \theta_1 } + d \quad \Leftrightarrow \quad \frac{ x_2 }{ \theta_2 } = \frac{ x_1 }{ \theta_1 } + d \tag{5.2.41} \] ここで、面1から面2に向かって伝搬している球面波を想定し、面1までの波面の半径を\(R_1\)、面2までの波面の半径を\(R_2\)とすると、式5.2.41は、 \[ R_2 = R_1+ d \tag{5.2.42} \] です。式5.2.42と式5.2.7が似ているという点がヒントになります。 | |
 | ヒントって言われてもなぁ。 | |
 | では、式5.2.36の1行目を2行目で割ってみましょう。 | |
 | えいっ!! \[ \frac{ x_2 }{ \theta_2 } = \frac{ A x_1 + B \theta_1 }{ C x_1 + D \theta_1 } \] | |
 | これを、\(R_1\)と\(R_2\)で表現できませんか?? | |
 | う〜ん。 \[ R_2 = \frac{ A \cfrac{x_1}{\theta_1} + B }{ C \cfrac{x_1}{\theta_1} + D } = \frac{ A R_1 + B }{ C R_1 + D } \tag{5.2.43} \] かな。 | |
 | というわけで、 \[ q_2 = \frac{ A q_1 + B }{ C q_1 + D } \tag{5.2.44} \] も成立しそうだ、ということが分かります | |
 | \(R\)(球面波の半径)と\(q\)(複素ビーム・パラメータ)がアナロジーだから?? | |
 | そうです。 | |
 | それ、ちょっと乱暴では?? | |
 | 乱暴でない証拠に、薄肉レンズで確認してみましょう。このときの出発点は式5.2.14になります。 | |
 | つまり、入射面は、 \[ \frac{ k }{ 2 q_1 } = \frac{ k }{ 2 R_1 } + \frac{ i }{ {\omega_1}^2 } \quad \left( \Leftrightarrow \quad \frac{ 1 }{ q_1 } = \frac{ 1 }{ R_1 } + i \frac{ 2 }{ k {\omega_1}^2 } \right) \tag{5.2.45} \] で、出射面は、 \[ \frac{ k }{ 2 q_2 } = \frac{ k }{ 2 R_2 } + \frac{ i }{ {\omega_2}^2 } \quad \left( \Leftrightarrow \quad \frac{ 1 }{ q_2 } = \frac{ 1 }{ R_2 } + i \frac{ 2 }{ k {\omega_2}^2 } \right) \tag{5.2.46} \] てことですね。 | |
 | ところが、さっきも言ったように、薄肉レンズは入射面の位置情報が、すべて出射面にそのまま転写されるので、\(\omega_1 = \omega_2 \)です。それを踏まえて、式5.2.46から式5.2.45を引くと―。 | |
 | ん〜と。 \[ \frac{ k }{ 2 q_2 } - \frac{ k }{ 2 q_1 } = \frac{ k }{ 2 R_2 } - \frac{ k }{ 2 R_1 } \quad \Leftrightarrow \quad \frac{ 1 }{ q_2 } = \frac{ 1 }{ R_2 } - \frac{ 1 }{ R_1 } + \frac{ 1 }{ q_1 } \tag{5.2.47} \] ですね。 | |
 | ここで、式5.2.40から、 \[ \frac{\theta_2}{x_2} = - \frac{1}{f} + \frac{\theta_1}{x_2} = - \frac{1}{f} + \frac{\theta_1}{x_1} \quad \Leftrightarrow \quad \frac{1}{R_2} = - \frac{1}{f} + \frac{1}{R_1} \tag{5.2.48} \] ですので、式5.2.48を式5.2.47に代入すると?? | |
 | こうかな。 \[ \frac{ 1 }{ q_2 } = - \frac{ 1 }{ f } + \frac{ 1 }{ q_1 } \tag{5.2.49} \] | |
 | 式5.2.48と式5.2.49は、同じ形をしてませんか?? | |
 | 本当だ…。 | |
 | つまり、\(R\)と\(q\)のアナロジーは薄肉レンズでも成立します。厳密なことを言えば、他のすべてのABCD行列で、このアナロジーが成立するかどうかは自明ではないので、確かに、議論が乱暴だという主張は間違いではありません。これをスッキリさせるためには、一般性が担保される別の議論が必要になりますが、それは少し面倒なので、ここでは端折りましょう。 |
〜1枚レンズ系〜
 | で、式5.2.44が成立すると、何が嬉しいんですか?? | |
 | Gaussianビームの伝搬を、式5.2.44を使って議論することが可能になります。 | |
 | ABCD行列そのものではなくて、式5.2.44を使うわけですね?? | |
 |
そうです。例えば、入射面から距離\(s_1\)の位置でビーム・ウェスト\({\omega_0}^{\left(1\right)}\)となっているGaussianビームが、薄肉レンズによって、出射面から距離\(s_2\)の位置でビーム・ウェスト\({\omega_0}^{\left(2\right)}\)に像変換されたケースを考えてみましょう。
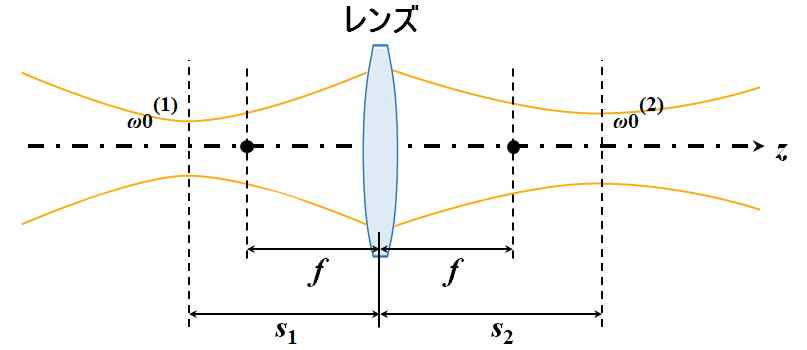 図5.2.22 薄肉レンズを介したGaussianビームの伝搬 |
|
 | このときのABCD行列は、 \[ \begin{align*} \left( \begin{array}{cc} A & B\\ C & D \end{array} \right) &= \left( \begin{array}{cc} 1 & s_2\\ 0 & 1 \end{array} \right) \left( \begin{array}{cc} 1 & 0\\ -\cfrac{1}{f} & 1 \end{array} \right) \left( \begin{array}{cc} 1 & s_1\\ 0 & 1 \end{array} \right) \\ &= \left( \begin{array}{cc} 1-\cfrac{s_2}{f} & s_1 + s_2\left( 1 - \cfrac{s_1}{f} \right) \\ -\cfrac{1}{f} & 1 - \cfrac{s_1}{f} \end{array} \right) \tag{5.2.50} \end{align*} \] かな?? | |
 | そうですね。式5.2.50は適宜、使っていくことにしましょう。ちなみに、式5.2.50の計算で用いた3つの行列はすべて行列式が\(1\)になるので、その結果であるABCD行列の行列式も\(1\)になります。 \[ AD-BC =1 \tag{5.2.51} \] | |
 | なるほど。 | |
 | ここでの議論は、ビーム・ウェストからビーム・ウェストへの変換に着目しているので、式5.2.45、式5.2.46において、\(R_1\)も\(R_2\)も\(\infty\)です。 | |
 | てことは、 \[ \begin{align*} \frac{ k }{ 2 q_1 } = \frac{ i }{ \{ {\omega_0}^{ \left( 1 \right) } \}^2 } \quad &\Leftrightarrow \quad \frac{ 2 q_1 }{ k } = - i \{ {\omega_0}^{ \left( 1 \right) } \}^2 \\ &\Leftrightarrow \quad q_1 = - i \frac{ k \{ {\omega_0}^{ \left( 1 \right) } \}^2 }{ 2 }= - i {z_0}^{ \left( 1 \right) } \tag{5.2.52} \end{align*} \] \[ \begin{align*} \frac{ k }{ 2 q_2 } = \frac{ i }{ \{ {\omega_0}^{ \left( 2 \right) } \}^2 } \quad &\Leftrightarrow \quad \frac{ 2 q_2 }{ k } = - i \{ {\omega_0}^{ \left( 2 \right) } \}^2 \\ &\Leftrightarrow \quad q_2 = - i \frac{ k \{ {\omega_0}^{ \left( 2 \right) } \}^2 }{ 2 }= - i {z_0}^{ \left( 2 \right) } \tag{5.2.53} \end{align*} \] ですね。 | |
 | というわけで、式5.2.44に式5.52と式5.2.53を代入します。 | |
 | !!何か、面倒な話になってきたな…。 \[ \begin{align*} -i {z_0}^{ \left( 2 \right) } &= \frac{-i {z_0}^{ \left( 1 \right) } A + B}{-i {z_0}^{ \left( 1 \right) } C + D} = \frac{\bigl[ -i {z_0}^{ \left( 1 \right) } A + B \bigr] \bigl[ i {z_0}^{ \left( 1 \right) } C + D \bigr] }{ \{ {z_0}^{ \left( 1 \right) } \}^2 C^2 + D^2} \\ &= \frac{ \{ {z_0}^{ \left( 1 \right) } \}^2 AC + BD -i {z_0}^{ \left( 1 \right) } \left( AD - BD \right) }{ \{ {z_0}^{ \left( 1 \right) } \}^2 C^2 + D^2} \\ &= \frac{ \{ {z_0}^{ \left( 1 \right) } \}^2 AC + BD -i {z_0}^{ \left( 1 \right) } }{ \{ {z_0}^{ \left( 1 \right) } \}^2 C^2 + D^2} \tag{5.2.54} \end{align*} \] 最後に、式5.2.51を使いましたけど…。 | |
 | 式5.2.54は常に成立するので、実部について、 \[ 0 = \frac{ \{ {z_0}^{ \left( 1 \right) } \}^2 AC + BD }{ \{ {z_0}^{ \left( 1 \right) } \}^2 C^2 + D^2} \quad \Leftrightarrow \quad \{ {z_0}^{ \left( 1 \right) } \}^2 AC + BD = 0 \tag{5.2.55} \] 虚部について、 \[ \begin{align*} {z_0}^{ \left( 2 \right) } = \frac{ {z_0}^{ \left( 1 \right) } }{ \{ {z_0}^{ \left( 1 \right) } \}^2 C^2 + D^2} \quad &\Leftrightarrow \quad \frac{ {z_0}^{ \left( 2 \right) } }{ {z_0}^{ \left( 1 \right) } } = \frac{ 1 }{ \{ {z_0}^{ \left( 1 \right) } \}^2 C^2 + D^2} \\ &\Leftrightarrow \quad \left( \frac{ {\omega_0}^{ \left( 2 \right) } }{ {\omega_0}^{ \left( 1 \right) } } \right)^2 = \frac{ 1 }{ \{ {z_0}^{ \left( 1 \right) } \}^2 C^2 + D^2} \tag{5.2.56} \end{align*} \] となりますね。 | |
 | なるほど。 | |
 | この式5.2.55と式5.2.56は重要な公式で、入射側の情報が分かれば、出射側のビーム・ウェスト位置は式5.2.50と式5.2.55から求まりますし、ビーム・ウェストは式5.2.56から求まります。式5.2.12や式5.2.13の\(z\)は、ビーム・ウェスト位置を原点としているので、出射側のビーム・ウェスト位置を改めて原点と置くことで、任意の\(z\)におけるGaussianビームのあらゆる情報が計算できることになります。 | |
 | そういうことか。いったん、ビーム・ウェスト位置とビーム・ウェストを求めるステップが必要なんですね。 | |
 | さて、式5.2.55に式5.2.50を代入してみましょう。 | |
 | これは大変そうだ…。 \[ \begin{align*} &- \{ {z_0}^{ \left( 1 \right) } \}^2 \left( 1-\frac{s_2}{f} \right) \frac{1}{f} + \left[ s_1 + s_2 \left( 1-\frac{s_1}{f} \right) \right] \left( 1 - \frac{s_1}{f} \right) = 0 \\ &\quad \Leftrightarrow \quad - \frac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{f} + \left( \frac{ {z_0}^{ \left( 1 \right) } }{f} \right)^2 s_2 + s_1 \left( 1 - \frac{s_1}{f} \right) + s_2 \left( 1-\frac{s_1}{f} \right)^2 = 0 \\ &\quad \Leftrightarrow \quad \left[ \left( \frac{ {z_0}^{ \left( 1 \right) } }{f} \right)^2 + \left( 1-\frac{s_1}{f} \right)^2 \right] s_2 = \frac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{f} - s_1 \left( 1 - \frac{s_1}{f} \right) \\ &\quad \Leftrightarrow \quad s_2 = \cfrac{ \cfrac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{f} - s_1 \left( 1 - \cfrac{s_1}{f} \right)}{ \left( \cfrac{ {z_0}^{ \left( 1 \right) } }{f} \right)^2 + \left( 1-\cfrac{s_1}{f} \right)^2 } \tag{5.2.57} \end{align*} \] | |
 | 次に、式5.2.56に式5.2.50を代入してみましょう。 | |
 | これは、そうでもないか…。 \[ \left( \frac{ {\omega_0}^{ \left( 2 \right) } }{ {\omega_0}^{ \left( 1 \right) } } \right)^2 = \cfrac{ 1 }{ \left( \cfrac{ {z_0}^{ \left( 1 \right) }}{f} \right)^2 + \left( 1 - \cfrac{s_1}{f} \right)^2} \tag{5.2.58} \] | |
 | それは1つの表現型ですね。 | |
 | ん??別の式があるってこと?? | |
 | そうです。 | |
 | 式5.2.58を変形していく?? | |
 | それでも導けますが、もう少し楽に計算するなら、式5.2.55を、 \[ \{ {z_0}^{ \left( 1 \right) } \}^2 = - \frac{BD}{AC} \tag{5.2.59} \] としておいて、式5.2.59を式5.2.56に代入します。 \[ \begin{align*} \left( \frac{ {\omega_0}^{ \left( 2 \right) } }{ {\omega_0}^{ \left( 1 \right) } } \right)^2 &= \cfrac{ 1 }{ - \cfrac{BD}{AC} C^2 + D^2} = \cfrac{ 1 }{ - \cfrac{BD}{A} C + D^2} \\ &= \cfrac{ 1 }{ \cfrac{D}{A} \left( AD - BC \right) } = \frac{ A }{ D } \tag{5.2.60} \end{align*} \] こうしておいて、式5.2.50を代入するとよいでしょう。 | |
 | う〜んと、 \[ \begin{align*} \left( \frac{ {\omega_0}^{ \left( 2 \right) } }{ {\omega_0}^{ \left( 1 \right) } } \right)^2 &= \cfrac{ 1-\cfrac{s_2}{f} }{ 1-\cfrac{s_1}{f} } = \frac{ f-s_2 }{ f-s_1 } \tag{5.2.61} \end{align*} \] かな。見た目が、ずいぶん簡単になりましたね。 | |
 |
以上が、1枚レンズ系によってGaussianビームがどのように変換されるか、の結果なんですが、もう少し議論を進めてみるために、式5.2.57の両辺の逆数をとって、
\[
\frac{1}{s_2} = \cfrac{ \left( \cfrac{ {z_0}^{ \left( 1 \right) } }{f} \right)^2 + \left( 1-\cfrac{s_1}{f} \right)^2 }{ \cfrac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{f} - s_1 \left( 1 - \cfrac{s_1}{f} \right)} \tag{5.2.62}
\]
式5.2.62の右辺の分子を次のように変形します。
\[
\begin{align*}
\left( \frac{ {z_0}^{ \left( 1 \right) } }{f} \right)^2 + \left( 1-\frac{s_1}{f} \right)^2 &=
\frac{ \{ {z_0}^{ \left( 1 \right) }\}^2 }{f^2} + 1 - \frac{2 s_1}{f} + \frac{{s_1}^2}{f^2} \\
&= \frac{ \{ {z_0}^{ \left( 1 \right) }\}^2 }{f^2} - \frac{s_1}{f} + \frac{{s_1}^2}{f^2} +1 - \frac{s_1}{f} \\
&= \frac{1}{f} \left( \frac{ \{ {z_0}^{ \left( 1 \right) }\}^2 }{f} - s_1 + \frac{{s_1}^2}{f} \right) +1 - \frac{s_1}{f} \\
&= \frac{1}{f} \left[ \frac{ \{ {z_0}^{ \left( 1 \right) }\}^2 }{f} - s_1 \left( 1 - \frac{s_1}{f} \right) \right] +1 - \frac{s_1}{f} \\
\end{align*}
\]
そのうえで、これを式5.2.62に代入すると、
\[
\begin{align*}
\frac{1}{s_2} &= \cfrac{ \cfrac{1}{f} \left[ \cfrac{ \{ {z_0}^{ \left( 1 \right) }\}^2 }{f} - s_1 \left( 1 - \cfrac{s_1}{f} \right) \right] }{ \cfrac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{f} - s_1 \left( 1 - \cfrac{s_1}{f} \right)} + \cfrac{ 1 - \cfrac{s_1}{f} }{ \cfrac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{f} - s_1 \left( 1 - \cfrac{s_1}{f} \right)} \\
&= \frac{1}{f} + \cfrac{ 1 }{ \cfrac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{f} \cdot \cfrac{f}{f-s_1}- s_1 }
= \frac{1}{f} + \cfrac{ 1 }{ \cfrac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{f-s_1}- s_1 } \\
& = \frac{1}{f} - \cfrac{ 1 }{ s_1 + \cfrac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{s_1 - f} }
\tag{5.2.63}
\end{align*}
\]
となります。式5.2.63はGaussianビームの伝搬を考慮に入れた薄肉レンズの公式として知られているもので、1983年にSelfよって導出されました(論文)。
 Sidney Self(1928〜2017) |
|
 | 幾何光学のレンズの公式とずいぶん違いますね。 | |
 |
そうですね。しかも、その振る舞いも、かなり異なります。それを分かりやすく示すように、更に式5.2.63の両辺に\(f\)を掛けて、変形してみましょう。
\[
\frac{f}{s_2} = 1 - \cfrac{ 1 }{ \cfrac{s_1}{f} + \cfrac{ \{ {z_0}^{ \left( 1 \right) } \}^2}{s_1 - f} \cdot \cfrac{1}{f} } = 1 - \cfrac{ 1 }{ \cfrac{s_1}{f} + \cfrac{ \left( \cfrac{{z_0}^{ \left( 1 \right) }}{f} \right)^2 }{\cfrac{s_1}{f} - 1} }
\tag{5.2.64}
\]
そして、\(\cfrac{s_2}{f}\)を縦軸、\(\cfrac{s_1}{f}\)を横軸にしてグラフにしたものが、図5.2.23です。
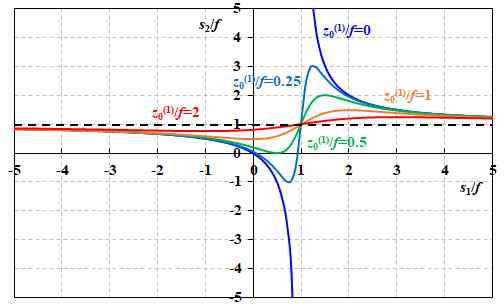 図5.2.23 Gaussianビームの伝搬を考慮に入れた薄肉レンズの公式 |
|
 | 幾何光学のレンズ公式と一致するのは、\(\cfrac{{z_0}^{ \left( 1 \right) }}{f} =0\)のときってこと?? | |
 | 厳密にはそうですが、薄肉レンズの焦点距離が長ければ、\(\cfrac{{z_0}^{ \left( 1 \right) }}{f} \approx 0\)なので、式5.2.64は、 \[ \begin{align*} \frac{f}{s_2} = 1 - \cfrac{ 1 }{ \cfrac{s_1}{f} } \quad &\Leftrightarrow \quad \frac{f}{s_2} = 1 - \frac{f}{s_1} \\ &\Leftrightarrow \quad \frac{1}{s_2} = \frac{1}{f} - \frac{1}{s_1} \tag{5.2.65} \end{align*} \] になり、幾何光学のレンズ公式と一致します。このことは、式5.2.57でも、分子の第1項、分母の第1項が無視できることから、 \[ \begin{align*} s_2 \approx \cfrac{ - s_1 \left( 1 - \cfrac{s_1}{f} \right)}{ \left( 1-\cfrac{s_1}{f} \right)^2 } \quad &\Leftrightarrow \quad \frac{1}{s_1} \left( 1-\frac{s_1}{f} \right) = -\frac{1}{ s_2 } \\ &\Leftrightarrow \quad \frac{1}{s_1} -\frac{1}{f} = -\frac{1}{ s_2 } \\ &\Leftrightarrow \quad \frac{1}{s_1} + \frac{1}{s_2} = \frac{1}{ f } \end{align*} \] のように確認できますね。 | |
 | \(\cfrac{{z_0}^{ \left( 1 \right) }}{f} =0\)って、\({z_0}^{ \left( 1 \right) } =0\)だから、\(k =0\)か\(\omega_0 =0\)でもありますね。 | |
 | はい。\(k =0\)ということは\(\lambda =0\)ですから、まさに幾何光学への近似ですし、\(\omega_0 =0\)は回折の影響が無視できるということですから、やはり幾何光学への近似になります。 | |
 | だから、この条件で幾何光学の公式と一致するのは当然、とも言えそうですね。 | |
 | また、式5.2.58は、 \[ \left( \frac{ {\omega_0}^{ \left( 2 \right) } }{ {\omega_0}^{ \left( 1 \right) } } \right)^2 \approx \cfrac{ 1 }{ \left( 1 - \cfrac{s_1}{f} \right)^2} \] ですが、式5.2.65の両辺に\(s_1\)を掛けると、 \[ \frac{s_1}{s_2} = \frac{s_1}{f} - 1 \] なので、 \[ \left( \frac{ {\omega_0}^{ \left( 2 \right) } }{ {\omega_0}^{ \left( 1 \right) } } \right)^2 = \cfrac{ 1 }{ \left( -\cfrac{s_1}{s_2} \right)^2} \Leftrightarrow \frac{ {\omega_0}^{ \left( 2 \right) } }{ {\omega_0}^{ \left( 1 \right) } } = \left| \cfrac{ s_2 }{ s_1} \right| \tag{5.2.66} \] となります。 | |
 | つまり、ビーム・ウェストはレンズの横倍率で変換されるってことか。これも、幾何光学と同じ結論ですね。 | |
 | ところが、この条件を外れると、たちまち幾何光学からは予測不能な奇妙な振る舞いを始めます。まず、図5.2.23を見て分かるのは、像側のビーム・ウェスト位置は最大値と最小値を持つ、ということです。 | |
 | そうですね。 | |
 | この極値がどこで出現するかと言うと―。 | |
 | 式5.2.57を微分すればいいか。 \[ \frac{d s_2}{d s_1} = \cfrac{-1 + \cfrac{2s_1}{f}}{\left( \cfrac{{z_0}^{\left(1 \right)}}{f}\right)^2 + \left(1 - \cfrac{s_1}{f} \right)^2 } + \cfrac{ \left[ \cfrac{\{ {z_0}^{\left(1\right)} \}^2}{f} -s_1 \left(1-\cfrac{s_1}{f} \right) \right] \cfrac{2}{f}\left(1-\cfrac{s_1}{f} \right) }{\left[ \left( \cfrac{{z_0}^{\left(1 \right)}}{f} \right)^2 + \left( 1 - \cfrac{s_1}{f} \right)^2 \right]^2 } = 0 \] これ、通分して、分子だけで計算すればいいですよね?? | |
 | そうですね。 | |
 | てことは、 \[ \begin{align*} {\rm Numer} &= \left( -1 + \frac{2s_1}{f}\right) \left[ \left( \frac{{z_0}^{\left(1 \right)}}{f}\right)^2 + \left(1 - \frac{s_1}{f} \right)^2 \right] \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad + \left[ \frac{\{ {z_0}^{\left(1\right)} \}^2}{f} -s_1 \left(1-\frac{s_1}{f} \right) \right] \frac{2}{f}\left(1-\frac{s_1}{f} \right) \\ &= -\left( \frac{{z_0}^{\left(1 \right)}}{f}\right)^2 - \left(1 - \frac{s_1}{f} \right)^2 + \frac{2s_1}{f} \left( \frac{{z_0}^{\left(1 \right)}}{f}\right)^2 + \frac{2s_1}{f} \left(1 - \frac{s_1}{f} \right)^2 \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad + 2 \left( \frac{{z_0}^{\left(1 \right)}}{f}\right)^2 - \frac{2s_1}{f} \left( \frac{{z_0}^{\left(1 \right)}}{f}\right)^2 - \frac{2s_1}{f} \left(1 - \frac{s_1}{f} \right)^2 \\ &= \left( \frac{{z_0}^{\left(1 \right)}}{f}\right)^2 - \left(1 - \frac{s_1}{f} \right)^2 = 0 \\ \end{align*} \] \[ \begin{align*} & \quad \quad \quad \quad \quad \Leftrightarrow \left( f-s_1 \right)^2 = \{{z_0}^{\left(1 \right)}\}^2 \\ & \quad \quad \quad \quad \quad \Leftrightarrow f-s_1 = \pm {z_0}^{\left(1 \right)} \quad \Leftrightarrow \quad s_1 = f \pm {z_0}^{\left(1 \right)} \tag{5.2.67} \end{align*} \] ですね。 | |
 | はい。ちなみに、\(s_1 = f + {z_0}^{\left(1 \right)}\)が最大値になります。 | |
 | さっきと逆に、\(f\)が短くなっていく(\(\cfrac{s_1}{f}\)が大きくなる)と、物側のビーム・ウェストがどこにあっても(\(\cfrac{{z_0}^{\left(1\right)}}{f}\)によらず)、像側のビーム・ウェストは焦点位置に現れる(\(\cfrac{s_2}{f}=1\))んですね。 | |
 | そういう見方もできますし、\({z_0}^{\left(1 \right)}\)と\(s_1\)を比較して、\({z_0}^{\left(1 \right)} \ll s_1\)でも\({z_0}^{\left(1 \right)} \gg s_1\)でも、像側のビーム・ウェストは焦点位置に現れると見ることもできます。 | |
 | 確かに、どちらの条件でも式5.2.63の右辺第2項は\(0\)に近似されるから、\(s_2 = f\)になりますね。 | |
 |
そして、おそらく最も奇妙に思えるのは、\(s_1=f\)のとき、像側のビーム・ウェストも焦点位置に現れる、という点でしょう。そのことは、式5.2.57で、\(s_1=f\)としたときに確認できます。
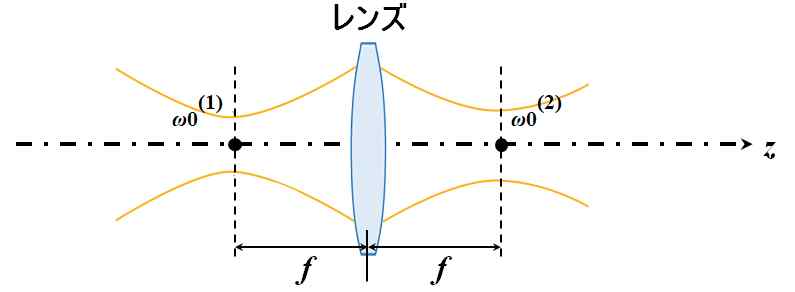 図5.2.24 Gaussianビームの奇妙な共役関係?? |
|
 | ん??あれ??物側の焦点位置に物体を置いたら、結像しないのでは?? | |
 | 幾何光学では。 | |
 | Gaussianビームでは、物側・像側の焦点位置が共役関係ってこと?? | |
 | そうではないですね。なぜなら、共役関係は幾何光学で定義されるからです。 | |
 | ということは、Gaussianビームでは共役関係は成立しないってこと?? | |
 | それも違います。共役関係はレンズの特性として議論されるので、Gaussianビームでも成立します。 | |
 | 何か禅問答みたいで、よく理解できないんですけど…。 | |
 | 至ってシンプルな話ですよ。幾何光学としての共役関係はGaussianビームでも成立する。だけど、ビーム・ウェストを共役関係で捉えてはいけない、と言っているだけです。もし、ビーム・ウェストを共役関係で捉えてよいとすれば、\(s_1=f\)のときは\(s_2=f\)なので、物側・像側のビーム・ウェストは一致してないといけませんが、式5.2.50で\(C = -\cfrac{1}{f}\)、\(D =0\)なので、式5.2.56から、 \[ \left( \frac{{\omega_0}^{\left(2 \right)}}{{\omega_0}^{\left(1 \right)}} \right)^2 = \left( \frac{f}{{z_0}^{\left(1\right)}} \right)^2 \quad \Leftrightarrow \quad \frac{{\omega_0}^{\left(2 \right)}}{{\omega_0}^{\left(1 \right)}} = \left| \frac{f}{{z_0}^{\left(1\right)}} \right| \tag{5.2.68} \] なので、一致しません。 | |
 | 今の教授の説明だと、「ビーム・ウェストを共役関係で捉えてはいけない」というところしか証明されてないのでは??「幾何光学としての共役関係はGaussianビームでも成立する」という証明にはなってないですよね?? | |
 | なるほど。その指摘は正しいですね。これを証明するためには、横倍率を\(\beta\)としたときに、互いに共役な面のABCD行列が、 \[ \left( \begin{array}{cc} A & B\\ C & D \end{array} \right) = \left( \begin{array}{cc} \beta & 0\\ \cfrac{1}{f} & \cfrac{1}{\beta} \end{array} \right) \tag{5.2.69} \] と表現できることを利用します。 | |
 | 式5.2.69を式5.2.44に代入すればいいわけですね?? | |
 | 実効的にはそうですが、その前に、計算を楽にするために、 \[ \frac{1}{q_2} = \frac{C q_1 + D }{A q_1 + B} = \cfrac{C + \cfrac{1}{q_1} D}{A + \cfrac{1}{q_1}B} \tag{5.2.70} \] という一工夫を入れておきましょう。 | |
 | そうか。こうしておくと、式5.2.45と式5.2.46が代入しやすくなるわけですね。 \[ \begin{align*} \frac{ 1 }{ R_2 } + i \frac{ 2 }{ k {\omega_2}^2 } &= \cfrac{C + \left( \cfrac{ 1 }{ R_1 } + i \cfrac{ 2 }{ k {\omega_1}^2 } \right) D}{A + \left( \cfrac{ 1 }{ R_1 } + i \cfrac{ 2 }{ k {\omega_1}^2 } \right) B} = \cfrac{ \left( C + \cfrac{ D }{ R_1 } \right) + i \cfrac{ 2D }{ k {\omega_1}^2 } }{ \left( A + \cfrac{ B }{ R_1 } \right) + i \cfrac{ 2B }{ k {\omega_1}^2 } } \\ &= \cfrac{ \left[ \left( C + \cfrac{ D }{ R_1 } \right) + i \cfrac{ 2D }{ k {\omega_1}^2 } \right] \left[ \left( A + \cfrac{ B }{ R_1 } \right) - i \cfrac{ 2B }{ k {\omega_1}^2 } \right] }{ \left( A + \cfrac{ B }{ R_1 } \right)^2 + \left( \cfrac{ 2B }{ k {\omega_1}^2 } \right)^2 } \\ &= \cfrac{ \left( A + \cfrac{ B }{ R_1 } \right) \left( C + \cfrac{ D }{ R_1 } \right) + \left( \cfrac{ 2 }{ k {\omega_1}^2 } \right)^2 BD }{ \left( A + \cfrac{ B }{ R_1 } \right)^2 + \left( \cfrac{ 2B }{ k {\omega_1}^2 } \right)^2 } \\ &\quad \quad \qquad + i \cfrac{ \left( A + \cfrac{ B }{ R_1 } \right) D - \left( C + \cfrac{ D }{ R_1 } \right) B }{ \left( A + \cfrac{ B }{ R_1 } \right)^2 + \left( \cfrac{ 2B }{ k {\omega_1}^2 } \right)^2 } \cdot \cfrac{ 2 }{ k {\omega_1}^2 } \tag{5.2.71} \end{align*} \] で、虚部どうしを比較して、 \[ \begin{align*} \frac{ 2 }{ k {\omega_2}^2 } &= \cfrac{ \left( A + \cfrac{ B }{ R_1 } \right) D - \left( C + \cfrac{ D }{ R_1 } \right) B }{ \left( A + \cfrac{ B }{ R_1 } \right)^2 + \left( \cfrac{ 2B }{ k {\omega_1}^2 } \right)^2 } \cdot \cfrac{ 2 }{ k {\omega_1}^2 } \\ &\quad \quad \quad \Leftrightarrow \left( \frac{ \omega_2 }{ \omega_1 } \right)^2 = \cfrac{ \left( A + \cfrac{ B }{ R_1 } \right)^2 + \left( \cfrac{ 2B }{ k {\omega_1}^2 } \right)^2 }{ \left( A + \cfrac{ B }{ R_1 } \right) D - \left( C + \cfrac{ D }{ R_1 } \right) B } \tag{5.2.72} \end{align*} \] になりますね。 | |
 | では、いよいよ式5.2.69を代入してください。 | |
 | \(B=0\)だから、殆ど消えちゃいますね…。 \[ \left( \frac{ \omega_2 }{ \omega_1 } \right)^2 = \frac{ A }{ D } = \beta^2 \quad \Leftrightarrow \quad \frac{ \omega_2 }{ \omega_1 } = \left| \beta \right| \tag{5.2.73} \] | |
 | 結果として、共役関係にあるビーム・スポット・サイズは横倍率で変換されるので、「幾何光学としての共役関係はGaussianビームでも成立する」わけです。 | |
 | 納得。でも、図5.2.24の関係が一般的に成立するとすれば、Gaussianビームでコリメート光を生成することは不可能ですね。 | |
 | そうなります。なので、できることはビーム拡がり角\(\theta_2\)を可能な限り小さくする、のみです。 | |
 | ということは、式5.2.20と式5.2.58から、 \[ \theta_2 = \frac{4}{k {\omega_0}^{\left( 2 \right)}} = \frac{4}{k {\omega_0}^{\left( 1 \right)}} \sqrt{\left( \frac{ {z_0}^{ \left( 1 \right) }}{f} \right)^2 + \left( 1 - \cfrac{s_1}{f} \right)^2} \tag{5.2.74} \] だから…。そうか。\(s_1 =f\)のときに、ビーム拡がり角も最小になるわけですね。 | |
 | そのうえで、\(\cfrac{{z_0}^{ \left( 1 \right) }}{f} \approx 0\)のときには\(\theta_2 \approx 0\)なので、コリメート光を得ることができる、つまり、幾何光学と同じ扱いになります。LSUの設計では、LDの発光点の大きさは高々数μm、対してコリメーター・レンズの焦点距離は数10mmなので、ほぼこの条件を満たしていると見なせて、コリメート光に変換できていると言えます。レーザ・ポインターがどこまでいってもコリメート光のように思えるのも、同じ理屈ですね。 | |
 | ということは、ここまでの議論は、実用的ではないってこと?? | |
 | そんなことはありません。特にレーザ・ビームを光ファイバーに導光するような場合は、以上のような議論が非常にデリケートな形で取り扱われます。ただ、LSUを題材にした場合、幾何光学的な取り扱いで近似してよい、ということなのです。 | |
 | だったら、ここまで長々と計算する必要ってあったんですか?? | |
 | そう言われると身も蓋もないですね。執筆者も、余計なところに足を突っ込んで、必要以上に数式を振りまわす事態になり、非常に後悔しているようです。 | |
 | 計算ミスしているかもしれませんしね。 | |
 | 執筆者も自信はないと言ってました。 | |
 | Latexに慣れてきたから、調子に乗っているだけなのでは??「生兵法は大怪我のもと」ですよ〜。 | |
 | …。 | |
 | 教授。どうしてGaussianビームは、こんな奇妙な振る舞いをするんですか?? | |
 | これまで扱ってきた波動は、平面波ならいつまでも平面波、球面波なら波源は固定というのが暗黙の前提でした。これを変えるためにはレンズを必要としたのです。しかし、Gaussianビームは、レンズを必要としなくても、ビームの性質として波面が目まぐるしく変わります。 | |
 | 式5.2.12ですね。 | |
 | よって、レンズの効果だけでなく、Gaussianビームの性質も合わさってレーザ・ビームが絞られます。こうやって絞られたレーザ・ビームがビーム・ウェストを生成するため、ビーム・ウェストだけに注目すると、奇妙な振る舞いをしているように見えるわけです。しかし、レンズそのものの性質が失われたわけではないので、式5.2.73のように、その名残も認めることができます。 | |
 | Gaussianビームの性質が失われるような条件だと、幾何光学の性質のみが表出するわけですね。 | |
 | その条件が、\(f\)が長いとき、\(\lambda\)が小さいとき、\(\omega_0\)が点のようにみなせるとき、ということになるのです。 |
| 前頁へ | 戻る | 次頁へ |