 |
収差と言ったら、Seidelの5収差が有名ですけど??
 Philipp Ludwig von Seidel(1821〜1896) |
|
 | そうですね。Seidelの5収差は光線収差に分類されるものです。 | |
 | レンズ系を出射した光線の、理想的な結像点からのズレが光線収差、でしたよね?? | |
 | そのズレを丁寧に分解し、重要なものを5つ選んだのがSeidel収差です。それぞれが独立した形で評価できますし、現象をビジュアル的に捉えることができるので、直感的に理解しやすいというメリットがあります。 | |
 | 波面収差というのは?? | |
 | 幾何光学的に1点に結像するということは、波動光学的に捉え直すと、球面波がその1点に向かって流れ込むということになります。像がぼやけるのは、その球面波が乱れているからなので、その乱れを表現したのものを波面収差と言います。 | |
 | メリットは?? | |
 | 波面収差は数式で収差の全容を大きく捉えることができるメリットがありますね。波面収差も見慣れてくれば、球面収差が支配的か、コマ収差が支配的か、といったようなことも理解できるようになります。 | |
 | で、どうして、レーザの章で波面収差を取り扱うんですか?? | |
 | なかなか鋭い質問ですね。執筆者によると、別に波面収差に触れなくても議論を進めることはできるということなのですが、乗り掛かった舟なので、取り上げることにしたみたいです。 | |
 | 大火傷するだけなのでは?? | |
 | そうですね。この議論も執筆者は自信がなさそうでした。 | |
 | だったら、やめた方が読者のためかもしれないですよ。 | |
 | そうかもしれませんが、まぁ、我々としてはお手並み拝見といきましょう。 | |
 | やれやれ…。教授、光線収差と波面収差は、何らかの関係が当然ありますよね?? | |
 |
ありますね。まずは、そこら辺から見ていきましょうか。そこで、まず図5.3.1のように、物面に光源S、そして瞳の中心を通過する主光線Sk0K0Q0(主光線が像面と交差する点をQ0)を定義します。
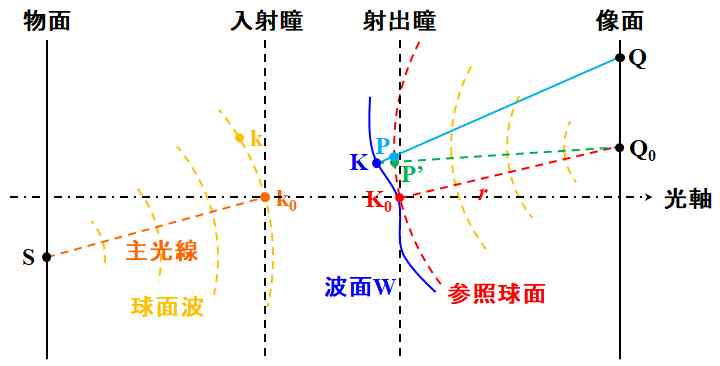 図5.3.1 波面収差を議論するための座標系 光源Sからは球面波が放射されているので、\(\overline{{\rm Sk}_0}\)を半径とした球面上にある点kは、レンズに収差がなければ、\(\overline{{\rm Q}_0{\rm K}_0}\)を半径とした球面上の(図示されていない)点に移動し、Q0に到達するはずです。ところが、レンズに収差があると、物側の点kを通過した光線は、Q0からズレた点Qに到達することになります。これを波面収差の観点から言い換えると、レンズを透過した点K0を通過する波面Wは、\(\overline{{\rm Q}_0{\rm K}_0} \equiv r\)を半径とした球面(この球面を参照球面と呼ぶ)からズレている、ということになるわけです。波面と光線の関係は?? |
|
 | 直交関係ですね。 | |
 | ということは、点kから移動した波面W上の点Kにおいて、波面Wの法線が光線KQと一致してないといけません。 | |
 | なるほど。 | |
 | 波面収差は、実際の波面の、参照球面からのズレと定義されるので、点Kにおける波面収差\(W_{\rm K}\)は\(\overline{\rm KP}\)です。 | |
 | 点Pは、光線KQと参照球面の交点ですね。 | |
 | 尚、この議論において、記号の上にあるバーは式1.8.6で計算される光路長と定義します。さて、ここで像側の状況に着目すると、 \[ \overline{{\rm K}{\rm Q}_0} = \overline{{\rm KP}^{\thinspace \prime}} + \overline{{\rm P}^{\thinspace \prime}{\rm Q}_0} \tag{5.3.1} \] となります。 | |
 | 点P'は、点Kと点Q0を結んだ線分と参照球面の交点か。 | |
 |
このとき、実際のレンズにおいては、点Qが点Q0からとんでもなく外れているということは起こらないので、
\[
\overline{{\rm KP}^{\thinspace \prime}} \approx \overline{{\rm KP}} = W_{\rm K} \tag{5.3.2}
\]
という近似が成立します。よって、点Q0を原点とする座標系を考え、点Kの座標を\(\left( x_{\rm K}, y_{\rm K}, z_{\rm K} \right)\)とすると、式5.3.1は、
\[
{x_{\rm K}}^2 + {y_{\rm K}}^2 + {z_{\rm K}}^2 = \left( W_{\rm K} + r \right)^2 \tag{5.3.3}
\]
と書き直すことができます。
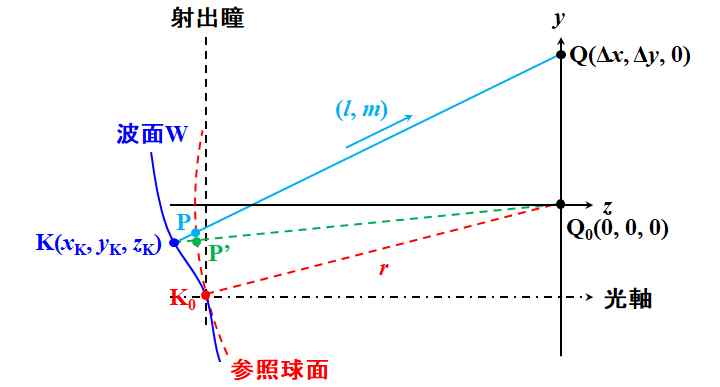 図5.3.2 射出瞳側の座標系 |
|
 | ここまでは、よさそうですね。 | |
 | ここで、\(r\)を充分に長く取れば、式5.3.3の右辺を展開したときの\({W_{\rm K}}^2\)の項は無視できるので、 \[ {x_{\rm K}}^2 + {y_{\rm K}}^2 + {z_{\rm K}}^2 \fallingdotseq 2 r W_{\rm K} + r^2 \tag{5.3.4} \] です。つまり、 \[ f \left(x_{\rm K} ,y_{\rm K} ,z_{\rm K} \right) \equiv {x_{\rm K}}^2 + {y_{\rm K}}^2 + {z_{\rm K}}^2 - 2r W_{\rm K} - r^2 = 0 \tag{5.3.5} \] で定義される\(f \left( x_{\rm K} ,y_{\rm K} ,z_{\rm K} \right) \)が、波面を表す方程式であると言えます。但し、\(x_{\rm K}\)、\(y_{\rm K}\)、\(z_{\rm K}\)は式5.3.4、或いは式5.3.5のため、お互い独立ではない点に留意しましょう。 | |
 | \(x_{\rm K}\)、\(y_{\rm K}\)を決めると、\(z_{\rm K}\)は自動的に決まってしまうわけですね。 | |
 | なので、\(W_{\rm K}\)は、\(x_{\rm K}\)、\(y_{\rm K}\)のみの関数である、と言うことができます。一方、 \[ \vec{\mathstrut {\rm Q}_0 {\rm Q}} = \vec{\mathstrut {\rm Q}_0 {\rm K}} + \vec{\mathstrut {\rm KQ}} \tag{5.3.6} \] が成立します。 | |
 | 今度はベクトル計算か。 | |
 | \(\vec{\mathstrut {\rm KQ}}\)について、何か言えませんか?? | |
 | う〜ん。 \[ \vec{\mathstrut {\rm KQ}} / \! / \nabla f \left( x_{\rm K}, y_{\rm K}, z_{\rm K} \right) \tag{5.3.7} \] かな。 | |
 | というわけで、点Qの座標を\( \left( \Delta x, \Delta y, 0 \right)\)、媒介変数を\(t\)とすると、式5.3.6は、 \[ \Delta x = x_{\rm K} + t \frac{\partial f}{\partial x_{\rm K}} = x_{\rm K} + t \left[ 2 x_{\rm K} - 2r \frac{\partial W_{\rm K}}{\partial x_{\rm K}} \right] \tag{5.3.8} \] \[ \Delta y = y_{\rm K} + t \frac{\partial f}{\partial y_{\rm K}} = y_{\rm K} + t \left[ 2 y_{\rm K} - 2r \frac{\partial W_{\rm K}}{\partial y_{\rm K}} \right] \tag{5.3.9} \] \[ 0 = z_{\rm K} + t \frac{\partial f}{\partial z_{\rm K}} = z_{\rm K} + 2t z_{\rm K} = \left( 1 + 2t \right) z_{\rm K} \tag{5.3.10} \] というように成分に分解して書くことができます。 | |
 | 点Qは任意なので、式5.3.10から、 \[ t = - \frac{1}{2} \tag{5.3.11} \] ですね。 | |
 | 式5.3.11を式5.3.8と式5.3.9に代入すると?? | |
 | えいっ!! \[ \Delta x = x_{\rm K} - x_{\rm K} + r \frac{\partial W_{\rm K}}{\partial x_{\rm K}} = r \frac{\partial W_{\rm K}}{\partial x_{\rm K}} \tag{5.3.12} \] \[ \Delta y = y_{\rm K} - y_{\rm K} + r \frac{\partial W_{\rm K}}{\partial y_{\rm K}} = r \frac{\partial W_{\rm K}}{\partial y_{\rm K}} \tag{5.3.13} \] | |
 | \(\left( \Delta x, \Delta y \right)\)は光線収差に他なりませんから、式5.3.12と式5.3.13が光線収差と波面収差の関係を示す重要な公式になります。が、ここで、より大胆な近似を導入しましょう。 | |
 | 大胆な近似って、回折を議論したときにもありましたね。 | |
 | はい。この大胆な近似は、回折の議論とのアナロジーで捉えると、射出瞳の大きさが\(r\)に対して充分に小さいという条件の下で成立すると考えてよさそうです。その近似とは、光線PQの方向余弦を\(\left(l,m \right)\)としたとき、 \[ l \approx \frac{x_{\rm K}}{r} \tag{5.3.14} \] \[ m \approx \frac{y_{\rm K}}{r} \tag{5.3.15} \] が成立するというものです。 | |
 | う〜ん。確かに大胆ですね〜。 | |
 | ですが、この大胆な近似が成立するなら、式5.3.12と式5.3.13は、 \[ \Delta x = \frac{\partial W_{\rm K}}{\partial l} \tag{5.3.16} \] \[ \Delta y = \frac{\partial W_{\rm K}}{\partial m} \tag{5.3.17} \] というように、更に簡単に書き表すことができます。 | |
 | この式だと、光線収差と波面収差が、微分と積分の関係にあることがハッキリしますね。 | |
 | Seidelの5収差は、収差の関数を多項式展開したときの次数で分類したものですが、光線収差で議論するのか、波面収差で議論するのか、で次数が1つ違ってくる点に注意しないといけません。 | |
 | そっか。でも、この議論は、上の大胆な近似が前提になってますけど、この前提は受け入れちゃって大丈夫ですか?? | |
 | たいていのレンズ系は無収差を目指して設計するので、大丈夫です。それと、この前提が受け入れられないと、少々面倒な話も出てきますしね。 | |
 | 面倒な話??具体的には?? | |
 | 波面収差の定義として、ここでは無批判に\(\overline{\rm KP}\)を採用しましたね?? | |
 | そうですね。でも、そんなに変な定義とは思えませんけど?? | |
 | そうでしょうか。点Pは参照球面上にあります。とすると、点Pを通過する理想的な光線は点Q0を通過しないといけません。理想的な光線と実際の光線において、ここに方向のズレが発生します。にも関わらず、\(\overline{\rm KQ}\)と\(\overline{\rm PQ}\)の光路長差を以て波面収差と定義することは正しいでしょうか?? | |
 | ムムム。そう言われると、困りますね。だって、点Q0を起点に考えると、\(\overline{{\rm KQ}_0}\)と\(\overline{{\rm P}^{\thinspace \prime} {\rm Q}_0}\)の光路長差が波面収差になるけど、これも結局、方向のズレが発生してますよね?? | |
 | そうです。波面収差の定義には、主光線をベースにする、実際の光線をベースにする、の2つの流儀があり得るわけです。それぞれには、それぞれの言い分があり、甲乙つけがたしの側面がありますが、何がややこしいと言って、1つの説明の中に流儀が混合する可能性が否定できないという点なのです。 | |
 | あ〜。つまり、片方の流儀で波面収差の計算をしているけど、回折積分するときはもう一方の流儀を採用して不整合を起こす、みたいな話ですね?? | |
 | これを、いちいちチェックしながら議論を進めるのは、正直、面倒です。 | |
 | 確かに。でも、大胆な近似が成立すれば、この辺のややこしい話は目を瞑っても大丈夫、ってことなんですね。 | |
 | そうです。但し、その背景には、以上のような考え方が隠されているということは、よく知っておいた方がいいでしょう。何でもかんでも、こういう計算が成立すると思い込んでしまうと、後で大変なミスを誘発するリスクを発生することにもなり兼ねませんからね。 |
〜回折理論、再び〜
 | 波面収差が分かったとして、それを考慮した回折像を計算しないといけませんよね?? | |
 | もちろんです。が、その前に、以前やった回折理論を、もう少し実用的な形に直して議論を進めることにしましょう。まず、式4.2.2を思い出してください。 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \iint_{\rm B} A \frac{\mathrm{e}^{ik {r_0}^{\thinspace \prime} }}{{r_0}^{\thinspace \prime}} \frac{\mathrm{e}^{ik r^{\thinspace \prime} }}{r^{\thinspace \prime}} d \Gamma \tag{4.2.2} \] 式4.2.2の被積分関数の\(A \cfrac{\mathrm{e}^{ik {r_0}^{\thinspace \prime} }}{{r_0}^{\thinspace \prime}}\)に着目すると、これは光源Sからの球面波でした。 | |
 | そうですね。 | |
 | しかし、ここで、Huygensの原理に立ち返ると、Huygensは最初のステップとして「ある波面Σを考えよ」と言っているだけで、「その波面は球面波でなければいけない」とまで限定してはいません。 | |
 | お、言われてみれば確かに。 | |
 | つまり、開口(孔)における複素振幅分布を、光源Sからの球面波によって得られたものと考えるのは、議論を進めるうえでは見通しがよくても、限定が少し強すぎるのです。 | |
 | だったら、より汎用性を持たせるために、任意の複素振幅分布を導入すればいいのでは?? | |
 | そうですね。そこで、この複素振幅分布を改めて瞳関数\(g \left(\xi, \eta \right) \)として、式4.2.2を、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \iint_{\rm B} g \left( \xi, \eta \right) \frac{\mathrm{e}^{ik r^{\thinspace \prime} }}{r^{\thinspace \prime}} d \Gamma \tag{5.3.18} \] のように書き換えます。こうしておいて、回折理論と同じ手順を踏むことにしましょう。 | |
 | そのときには、式5.3.18の被積分関数の分母の\(r^{\thinspace \prime}\)は\(r\)に、指数関数の\(r^{\thinspace \prime}\)は式4.2.4に置き換えましたね。 | |
 | つまり、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \frac{\mathrm{e}^{ikr}}{r} \iint_{\rm B} g \left( \xi, \eta \right) \exp \left[ ik \left( - \frac{x \xi + y \eta}{ r } + \frac{ \xi^2 + \eta^2 }{ 2 r } \right) \right] d \Gamma \tag{5.3.19} \] です。 | |
 | 式5.3.19で、 \[ \frac{ \xi^2 + \eta^2 }{\lambda} \ll r \tag{5.3.20} \] のとき、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \frac{\mathrm{e}^{ikr}}{r} \iint_{\rm B} g \left( \xi, \eta \right) \exp \left[ -ik \frac{x \xi + y \eta}{ r }\right] d \Gamma \tag{5.3.21} \] に近似されて、Fraunhofer回折が適用されるってこと?? | |
 | そのとおりです。 | |
 | 教授。何か、前の議論のページと行ったり来たりで、凄く分かりづらいんですけど。 | |
 | そうですね。本当なら、この議論は回折理論のところで片づけておくべきでした。 | |
 | これも、執筆者のせい?? | |
 | 行き当たりばったりに執筆しているので、こういう事態を招いてしまったようです。でも、執筆者も大いに反省しているようなので、そこは寛大な心で許してあげましょう。 | |
 | しょうがないなぁ。 | |
 | いずれにしても、式5.3.21については、同じように方向余弦や空間周波数を定義することで、「Fraunhofer回折の振幅分布は瞳関数の2次元Fourier変換に比例する」という同様の結果を得ることができます。 | |
 | 次はFresnel回折ですね。 | |
 | これは、式5.3.18の被積分関数の分母の\(r^{\thinspace \prime}\)を\(R\)に、指数関数の\(r^{\thinspace \prime}\)を式4.3.3に置き換えればOKです。 | |
 | てことは、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \frac{\mathrm{e}^{ikz}}{R} \iint_{\rm B} g \left( \xi, \eta \right) \exp \left[ ik \frac{ \left( x - \xi \right)^2 + \left( y - \eta \right)^2 }{ 2 z } \right] d \Gamma \tag{5.3.22} \] かな?? | |
 | でもよいですし、\(R \fallingdotseq z\)として、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \frac{\mathrm{e}^{ikz}}{z} \iint_{\rm B} g \left( \xi, \eta \right) \exp \left[ ik \frac{ \left( x - \xi \right)^2 + \left( y - \eta \right)^2 }{ 2 z } \right] d \Gamma \tag{5.3.23} \] でもいいでしょう。 | |
 | でも、ここまでは、以前の議論の単なる焼き直しでは?? | |
 |
はい。そこで、いよいよ波面収差を導入します。図4.2.1と対応づけるために、図5.3.2を改めて描き直しましょう。
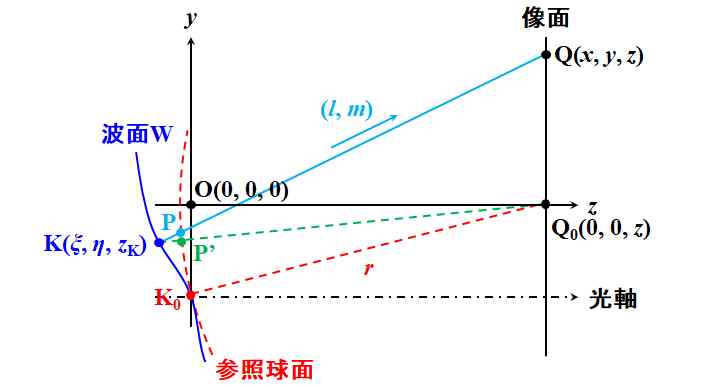 図5.3.3 波面収差を考慮した回折 |
|
 | ん〜と。座標原点を射出瞳側に移動させたのか。それと、点Kの座標が\(\left(\xi, \eta ,z_{\rm K} \right)\)に、点Qの座標が\(\left(x, y, z \right)\)に変更ですね。 | |
 | このとき、\(\overline{\rm KQ} = r^{\thinspace \prime \prime} \)とすると、式5.3.18は、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \iint_{\rm B} g \left( \xi, \eta \right) \frac{\mathrm{e}^{ik r^{\thinspace \prime \prime} }}{r^{\thinspace \prime \prime}} d \Gamma \tag{5.3.24} \] と修正されますが、\(\overline{\rm PQ} = r^{\thinspace \prime}\)とすると、 \[ \overline{\rm KQ} = \overline{\rm KP} + \overline{\rm PQ} = W_{\rm K} + r^{\thinspace \prime} \tag{5.3.25} \] なので、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \iint_{\rm B} g \left( \xi, \eta \right) \mathrm{e}^{ik W_{\rm K} } \frac{\mathrm{e}^{ik r^{\thinspace \prime} }}{r^{\thinspace \prime \prime}} d \Gamma \tag{5.3.26} \] です。更に、\(z_{\rm K}\)も微小なので\(0\)とし、\(r^{\thinspace \prime \prime} \fallingdotseq r^{\thinspace \prime}\)も言えそうなので、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \iint_{\rm B} g \left( \xi, \eta \right) \mathrm{e}^{ik W \left( \xi, \eta \right) } \frac{\mathrm{e}^{ik r^{\thinspace \prime} }}{r^{\thinspace \prime}} d \Gamma \tag{5.3.27} \] が、波面収差を考慮した回折計算になるわけです。 | |
 | Bは、射出瞳の大きさですか?? | |
 | この計算では、そうなりますね。式5.3.27以降は、式5.3.18以降の議論の繰り返しです。 | |
 | 図4.2.1と図5.3.3では、式5.3.27以降で展開される近似に微妙な違いがあるように見えますけど。 | |
 | 近似の観点からは同じですよ。図4.2.1の場合は、点Qを起点に、\(\overline{\rm PQ} \fallingdotseq \overline{\rm OQ}\)(\(r^{\thinspace \prime} \fallingdotseq r \))としたわけですが、図5.3.3の場合は、点Pを起点に、\(\overline{\rm PQ} \fallingdotseq \overline{{\rm PQ}_0}\)(\(r^{\thinspace \prime} \fallingdotseq r \))とすればよいのです。 | |
 | 何だか近似が過ぎるようにも思うんですけど、式5.3.18と見比べると、被積分関数に波面収差を示す因子\(\mathrm{e}^{ik W \left( \xi, \eta \right) }\)を演算すればよい、という感じなのかな?? | |
 | 煎じ詰めれば、そういうことです。 | |
 | ということは、Fraunhofer回折は、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \frac{\mathrm{e}^{ikr}}{r} \iint_{\rm B} g \left( \xi, \eta \right) \mathrm{e}^{ik W \left( \xi, \eta \right) } \exp \left[ -ik \frac{x \xi + y \eta}{ r }\right] d \Gamma \tag{5.3.28} \] ってこと?? | |
 | そうです。 | |
 | \(r\)は参照球面の半径?? | |
 | そうです。 | |
 | で、Fresnel回折の場合は、 \[ U \left( {\rm Q} \right) = - \frac{i}{\lambda} \cos \delta \frac{\mathrm{e}^{ikz}}{z} \iint_{\rm B} g \left( \xi, \eta \right) \mathrm{e}^{ik W \left( \xi, \eta \right) } \exp \left[ ik \frac{ \left( x - \xi \right)^2 + \left( y - \eta \right)^2 }{ 2 z } \right] d \Gamma \tag{5.3.29} \] ってこと?? | |
 | そうです。 | |
 | 結構、苦労して議論をやり直したわりに、結果は大したことないですね…。 |
| 前頁へ | 戻る | 次頁へ |