 | Seidelの5収差は、レンズ設計をする際に、その性能を評価するうえで非常に重要な指針となるものですが、波面収差も同じことが言えます。 | |
 | つまり、波面収差が\(0\)になれば「いいレンズ」ってことですね。 | |
 | そうなんですが、波面収差を\(0\)にすることは難しいです。そこで、波面収差をどこまで抑えたら「いいレンズ」と言えるのか、という議論が必要になります。 | |
 | なるほど。 | |
 | これについて、最初に言及したのはRayleighで、「波面収差の(絶対値の)最大値が、波長の\(\cfrac{1}{4}\)以下」と定義する(論文)ものです。これをRayleigh's criterionと言います。 | |
 | Rayleighと言えば、以前、Rayleighの解像限界っていうのもありましたね。 | |
 | あちらは、Rayleigh's limitとも呼ばれるもので、無収差レンズでも光の波動性によって、2つの物体がこれ以上近づくと分離できない間隔限界が存在する、というものでした。こちらは、レンズに収差があっても、無収差レンズとみなせる限界の波面収差の意味になります。 | |
 | 何だか、ややこしいな〜。この定義は、理論的なものなんですか?? | |
 | 経験的なものです。なので、提案というのに近いですね。 | |
 | その提案は受け入れられるもの?? | |
 | そうですね。そのレンズが、どういう用途に用いられるかに依存しますが、実用的には問題ないとは思います。 | |
 | Rayleigh's criterionでは不足するケースもある?? | |
 | ありますね。そもそも、Rayleighは天体観測用のレンズを念頭に、この指針を提案してますし、もっと収差を厳しく管理しなければ役に立たない用途は山ほどあります。それと、波面収差の良し悪しを最大値で評価するのは、ちょっと無理があるんですよ。 | |
 | そうですか?? | |
 | 例えば、レンズの有効径を考えて、その中に最大値が1つだけある波面収差と、無数にある波面収差とで、それら2つのレンズの性能が同じとは、とても思えませんよね?? | |
 | 言われてみると、なるほどですね。とすると、全体的な傾向を評価できる指標がほしくなりますね。 | |
 |
そこで、Rayleigh's criterionに代わる指標をMaréchalが提案します。
 Robert Gaston André Maréchal(1916〜2007) |
|
 | Maréchal's criterion?? | |
 | はい。これは、「波面収差の標準偏差が、波長の\(\cfrac{1}{14}\)以下」であれば無収差レンズとみなしてよい、という定義になります。 | |
 | 標準偏差だと、最大値がどのくらい散らばっているかは分かるかもしれないけど、レンズの有効径の中に満遍なく散らばっているのか、ある狭い領域だけに固まっているのか、分からないのでは?? | |
 | そうですね。なので、波面収差を評価する場合、あれこれ処理した1つの数値で議論することはできない、ということです。ですが、実用的には非常に便利なので、Rayleigh's criterionにしろMaréchal's criterionにしろ、よく使われますね。 | |
 | で、そのMaréchal's criterionとは?? | |
 | Maréchal's criterionは、参照球面の中心における強度(中心強度)に着目した指標になります。 | |
 | 図5.3.3の点Q0ですね。 | |
 | このとき、式5.3.25は、 \[ \overline{{\rm KQ}_0} = \overline{{\rm KP}^{\thinspace \prime}} + \overline{{\rm P}^{\thinspace \prime}{\rm Q}}_0 = W_{\rm K} + r \tag{5.3.30} \] と書き直せます。 | |
 | そうすると、式5.3.26は、 \[ U \left( {\rm Q}_0 \right) = - \frac{i}{\lambda} \cos \delta \iint_{\rm B} g \left( \xi, \eta \right) \mathrm{e}^{ik W_{\rm K} } \frac{\mathrm{e}^{ik r}}{r^{\thinspace \prime \prime}} d \Gamma \tag{5.3.31} \] ですね。 | |
 | 式5.3.31の被積分関数にある\(r^{\thinspace \prime \prime}\)は、Fraunhofer回折にしろ、Fresnel回折にしろ、近似して定数扱いにしてましたから、ここでは\(r\)に近似してしまうと、\(\cfrac{\mathrm{e}^{ik r}}{r}\)を被積分関数の外に出すことができます。 \[ U \left( {\rm Q}_0 \right) = - \frac{i}{\lambda} \frac{\mathrm{e}^{ik r}}{r} \cos \delta \iint_{\rm B} g \left( \xi, \eta \right) \mathrm{e}^{ik W_{\rm K} } d \Gamma \tag{5.3.32} \] では、強度\(I\)を求めてください。 | |
 | 式5.3.32を2乗すればいいから、 \[ I \left( {\rm Q}_0 \right) = \left| U \left( {\rm Q}_0 \right) \right|^2 = \left( \frac{\cos \delta}{\lambda r} \right)^2 \left| \iint_{\rm B} g \left( \xi, \eta \right) \mathrm{e}^{ik W_{\rm K} } d \Gamma \right|^2 \tag{5.3.33} \] かな。 | |
 | 無収差だったら?? | |
 | それは、 \[ I \left( {\rm Q}_0 \right) = \left( \frac{\cos \delta}{\lambda r} \right)^2 \left| \iint_{\rm B} g \left( \xi, \eta \right) d \Gamma \right|^2 \tag{5.3.34} \] ですね。 | |
 | そうすると、式5.3.33、式5.3.34の比をとった、 \[ {\mathcal S} \left( {\rm Q}_0 \right) = \frac{ \left| \displaystyle \iint_{\rm B} g \left( \xi, \eta \right) \mathrm{e}^{ik W_{\rm K} } d \Gamma \right|^2 }{ \left| \displaystyle \iint_{\rm B} g \left( \xi, \eta \right) d \Gamma \right|^2 } \tag{5.3.35} \] という量を定義する(論文)ことができます。これをStrehl definitionと言います。実は、\({\mathcal S}\)も波面収差の良し悪しを評価する指標になるんですよ。 | |
 | ん??波面収差そのものではなく、集光したビームの中心強度で代用するってこと?? | |
 |
そういうことです。Strehlは\({\mathcal S}\)に着目して、「\({\mathcal S} \ge 0.8\)のとき無収差レンズとみなす」と定義しています(論文)。これをStrehl ratioと言います。
 Karl Wilhelm Andreas Strehl(1864〜1940) |
|
 |
波面収差があれば、ビーム・スポットが広がって、その分、中心強度も下がるってことか。
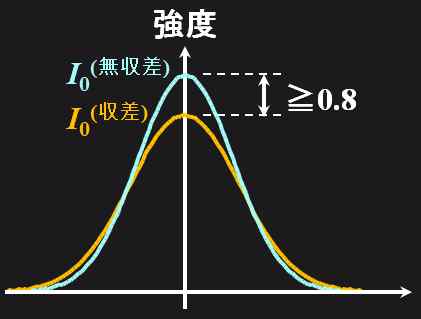 図5.3.4 Strehl ratio |
|
 | はい。エネルギーは保存されるので、そうなってないとおかしいです。 | |
 | これって、Rayleigh's criterionと何か関係があるんですか?? | |
 | 無関係ではありません。そのことを調べるために、次のようなことを考えてみましょう。無収差レンズがあって、それに平面波が入射したとき、像側はどうなりますか?? | |
 | レンズの焦点位置で結像しますよね。あ、でも波動光学的には回折像になりますけど。 | |
 | 今、円形開口を仮定すると、Fraunhofer回折の場合、それは式4.2.28のような複素振幅分布で与えられます。 \[ U \left( w \right) = C_0 \int_{0}^{\rho_0} 2 \pi J_0 \left( 2 \pi \rho w \right) \rho d \rho \tag{4.2.28} \] | |
 | あ〜、以前やりましたね。 | |
 | では、焦点位置から\(\Delta z\)だけずれたら、そのビーム・スポットはどうなりますか?? | |
 | そりゃ、太っていきますよ。 | |
 | なぜですか?? | |
 | え??なぜ?? | |
 | ビーム・スポットが太ったという現象について、収差の観点から何か言えませんか?? | |
 | そういう意味か。焦点位置からずれたら、参照球面の半径が変わるので、その変化の分、波面収差が乗ってくるから、ですね。 | |
 | そうすると、その波面収差の量と、中心強度の変化との間に、何か関係性が見出せそうですね?? | |
 | お。ということは、\(\Delta z\)を大きくしていって、中心強度が\(80\%\)にダウンしたときの波面収差が、\(\cfrac{\lambda}{4}\)に相当するってことか。 | |
 | では、確認してみましょう。まず、式4.2.28を、波面収差を考慮した形に修正します。 | |
 | こうかな。 \[ U \left( w \right) = C_0 \int_{0}^{\rho_0} 2 \pi {\mathrm{e}^{ik W_{\rm K}}} J_0 \left( 2 \pi \rho w \right) \rho d \rho \tag{5.3.36} \] | |
 |
では、具体的に波面収差の形を求めてみましょう。
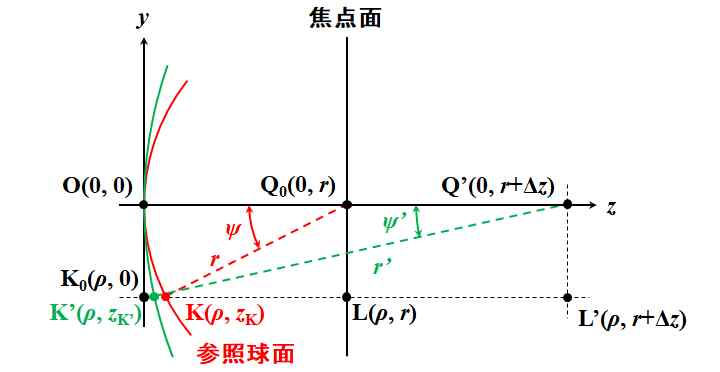 図5.3.5 デフォーカスしたときの波面収差を議論するための座標系 まず、図5.3.5において、焦点面における結像位置をQ0とし、ここから\(\Delta z\)デフォーカスした位置をQ'とします。このとき、参集球面の半径が\(r\)から\(r^{\thinspace \prime}\)に変わったとしましょう。半径\(r\)の参照球面の中心角\(\psi\)の、参照球面上の点をKと置き、その座標を\(\left( \rho, z_{\rm K} \right)\)とします。 |
|
 | ここの議論は、回転対称形を前提としているから、実際は3次元でも、2軸で議論できるってことですね。 | |
 | デフォーカスによって発生した波面収差\(W_{\rm K}\)は、近似的に\(\overline{{\rm KK}^{\thinspace \prime}}\)と見なすことができます。 | |
 | てことは、 \[ W_{\rm K} = \overline{{\rm KK}^{\thinspace \prime}} = \overline{{\rm KK}_0} - \overline{{\rm K}^{\thinspace \prime}{\rm K}_0} = r \left( 1- \cos \psi \right) - r^{\thinspace \prime} \left( 1- \cos \psi^{\thinspace \prime} \right) \tag{5.3.37} \] か。でも、どうせ\(\Delta z\)は微小だから、\(\psi \fallingdotseq \psi^{\thinspace \prime}\)ってことですよね?? | |
 | ついでに、\(r^{\thinspace \prime} = r + \Delta z\)も考慮すると?? | |
 | ん〜と。 \[ W_{\rm K} = r \left( 1- \cos \psi \right) - \left( r + \Delta z \right) \left( 1- \cos \psi \right) = - \Delta z \left( 1- \cos \psi \right) \tag{5.3.38} \] ですね。 | |
 | ここで、\(x\)が小さいとき、 \[ \sqrt{ 1 - x^2 } \approx 1 - \frac{x^2}{2} \] という近似式が成立することに着目し、\(x= \sin \psi\)とすると、 \[ \sqrt{ 1 - \sin^2 \psi } = 1 - \frac{\sin^2 \psi}{2} \quad \Leftrightarrow \quad \cos \psi = 1 - \frac{\sin^2 \psi}{2} \quad \Leftrightarrow \quad 1 - \cos \psi = \frac{\sin^2 \psi}{2} \] となるので―。 | |
 | そんな近似式があるのか…。そうすると、式5.3.38は、 \[ W_{\rm K} = - \Delta z \frac{\sin^2 \psi}{2} \tag{5.3.39} \] になるわけですね。結構、すっきりしたな。 | |
 | 更に、 \[ \sin \psi = \frac{\rho}{r} \] なので、 \[ W_{\rm K} = - \frac{\Delta z}{2} \left( \frac{\rho}{r} \right)^2 \tag{5.3.40} \] です。今、興味の対象は中心強度なので、式5.3.36において、\(w=0\)とすればよく、\(J_0\left(0 \right) =1\)を考慮し、式5.3.40を代入すると、 \[ U \left( 0 \right) = C_0 \int_{0}^{\rho_0} 2 \pi \exp \left[ -i k \frac{\Delta z}{2} \left( \frac{\rho}{r} \right)^2 \right] \rho d \rho \tag{5.3.41} \] となります。 \[ C_1 \equiv -k \frac{ \Delta z }{4 r^2} \tag{5.3.42} \] として、式5.3.41を積分すると?? | |
 | えっと。 \[ \begin{align*} U \left( 0 \right) &= C_0 \int_{0}^{\rho_0} 2 \pi \mathrm{e}^{ 2 i C_1 \rho^2 } \rho d \rho = \frac{\pi}{2i} \frac{C_0}{C_1} \left[ \mathrm{e}^{ 2 i C_1 \rho^2 } \right]^{\rho_0}_0 \\ &= \frac{\pi}{2i} \frac{C_0}{C_1} \left( \mathrm{e}^{ 2 i C_1 {\rho_0}^2 } - 1 \right) = \frac{\pi}{2i} \frac{C_0}{C_1} \mathrm{e}^{ i C_1 {\rho_0}^2 } \left( \mathrm{e}^{ i C_1 {\rho_0}^2 } - \mathrm{e}^{ -i C_1 {\rho_0}^2 } \right) \\ &= \pi \frac{C_0}{C_1} \mathrm{e}^{ i C_1 {\rho_0}^2 } \sin C_1 {\rho_0}^2 = \pi C_0 {\rho_0}^2 \mathrm{e}^{ i C_1 {\rho_0}^2 } \frac{\sin C_1 {\rho_0}^2}{C_1 {\rho_0}^2} \tag{5.3.43} \end{align*} \] かな。 | |
 | よって、中心強度は、 \[ I \left( {\rm Q}_0 \right) = \left| U \left( 0 \right) \right|^2 = \left( \pi C_0 {\rho_0}^2 \right)^2 \left( \frac{\sin C_1 {\rho_0}^2}{C_1 {\rho_0}^2} \right)^2 \tag{5.3.44} \] です。無収差のときの中心強度は、当然、 \[ I \left( {\rm Q}_0 \right) = \left( \pi C_0 {\rho_0}^2 \right)^2 \tag{5.3.45} \] ですから、Strehl difinitionは、 \[ {\mathcal S} \left( {\rm Q}_0 \right) = \left( \frac{\sin C_1 {\rho_0}^2}{C_1 {\rho_0}^2} \right)^2 \tag{5.3.46} \] となります。さて、ここで\(C_1 {\rho_0}^2=\cfrac{\pi}{4}\)としてみましょう。 | |
 | 分子が\(\cfrac{1}{\sqrt{2}}\)だから、\({\mathcal S}\)は\(0.9\)の2乗で、約\(80\%\)ですね。 | |
 | まず、Strehl ratioが求まりました。一方、波面収差の最大値は、式5.3.40から、 \[ W_{\rm K} = - \frac{\Delta z}{2} \left( \frac{\rho_0}{r} \right)^2 = - \frac{2}{k} \cdot k \frac{\Delta z}{4 r^2} {\rho_0}^2 = \frac{2}{k} \cdot C_1 {\rho_0}^2 = \frac{2 \lambda}{2 \pi} \cdot \frac{\pi}{4} = \frac{\lambda}{4} \tag{5.3.47} \] となり、Rayleigh's criterionが得られます。 | |
 |
なるほど。確かに関係はありそうですね。でも、教授。ここまでの議論は、デフォーカスによる波面収差に限定した話ですよね??このときの波面収差って、お椀のような形状になっていると思うんですけど、この前、実際のレンズを測定したときの波面収差って、グニャグニャしてましたよ??
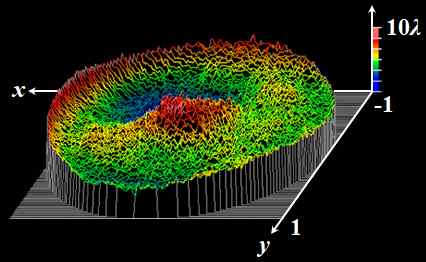 図5.3.6 波面収差 |
|
 | そうですね。確かに、以上の議論を一般論に敷衍させるのは無理がある、と言われても仕方がないと思います。でも、前にも言ったように、レンズを設計するのも加工するのも、基本的には無収差を目指しますし、その範疇において、Rayleigh's criterionがStrehl ratioと大きく外れるということは経験的にないですね。実用的な運用で考えれば、一般論とのギャップを気にする必要は殆どありません。 | |
 | で、Maréchal's criterionの方はどうなったんですか?? | |
 | そうでした。横道に反れてしまいましたが、式5.3.35に戻りましょう。ここで、\(\mathrm{e}^{ikW_{\rm K}}\)をTaylor展開します。 | |
 | 何次までですか?? | |
 | 2次までで充分ですね。 | |
 | そうすると…。 \[ \mathrm{e}^{ikW_{\rm K}} = 1 + ikW_{\rm K} +\frac{\left( ikW_{\rm K} \right)^2}{2} = 1 + ikW_{\rm K} -\frac{k^2 {W_{\rm K}}^2 }{2} \tag{5.3.48} \] ですね。 | |
 | よって、式5.3.35の分子は、議論を簡潔にするために、\(g \left( \xi, \eta \right)\)をB内部のとき\(1\)、B外部のとき\(0\)とすると、 \[ \begin{align*} &\left| \displaystyle \iint_{\rm B} \mathrm{e}^{ik W_{\rm K} } d \Gamma \right|^2 = \left| \displaystyle \iint_{\rm B} \left[ 1 + ikW_{\rm K} -\frac{k^2 {W_{\rm K}}^2}{2} \right] d \Gamma \right|^2 \\ &\quad \quad \quad \quad = \left( \displaystyle \iint_{\rm B} \left[ 1 -\frac{k^2 {W_{\rm K}}^2}{2} \right] d \Gamma \right)^2 + \left( \displaystyle \iint_{\rm B} kW_{\rm K} d \Gamma \right)^2 \\ &\quad \quad \quad \quad \approx \left( \displaystyle \iint_{\rm B} d \Gamma \right)^2 - k^2 \displaystyle \iint_{\rm B} d \Gamma \displaystyle \iint_{\rm B} {W_{\rm K}}^2 d \Gamma + k^2 \left( \displaystyle \iint_{\rm B} W_{\rm K} d \Gamma \right)^2 \tag{5.3.49} \end{align*} \] となります。 | |
 | ここでも、2次よりも高次の項は無視するのか…。 | |
 | 式5.3.49を式5.3.35に代入すると、 \[ \begin{align*} {\mathcal S} \left( {\rm Q}_0 \right) &= \frac{ \left( \displaystyle \iint_{\rm B} d \Gamma \right)^2 - k^2 \displaystyle \iint_{\rm B} d \Gamma \displaystyle \iint_{\rm B} {W_{\rm K}}^2 d \Gamma + k^2 \left( \displaystyle \iint_{\rm B} W_{\rm K} d \Gamma \right)^2 }{ \left( \displaystyle \iint_{\rm B} d \Gamma \right)^2 } \\ &= 1 - k^2 \left[ \frac{ \displaystyle \iint_{\rm B} {W_{\rm K}}^2 d \Gamma }{ \displaystyle \iint_{\rm B} d \Gamma } - \left( \frac{ \displaystyle \iint_{\rm B} W_{\rm K} d \Gamma }{ \displaystyle \iint_{\rm B} d \Gamma } \right)^2 \right] \tag{5.3.50} \end{align*} \] となります。さて、波面収差の平均値\(\mu_{\rm W}\)は、どう書けますか?? | |
 | \(\mu_{\rm W}\)か…。ん〜と。 \[ \mu_{\rm W} = \frac{ \displaystyle \iint_{\rm B} W_{\rm K} d \Gamma }{ \displaystyle \iint_{\rm B} d \Gamma } \tag{5.3.51} \] では?? | |
 | そうすると、式5.3.50は、 \[ {\mathcal S} \left( {\rm Q}_0 \right) = 1 - k^2 \left[ \frac{ \displaystyle \iint_{\rm B} {W_{\rm K}}^2 d \Gamma }{ \displaystyle \iint_{\rm B} d \Gamma } - {\mu_{\rm W}}^2 \right] \tag{5.3.52} \] となります。一方で、波面収差の分散\({\sigma_{\rm W}}^2\)は、 \[ \begin{align*} {\sigma_{\rm W}}^2 &= \frac{ \displaystyle \iint_{\rm B} \left( {W_{\rm K}} - \mu_{\rm W} \right)^2 d \Gamma }{ \displaystyle \iint_{\rm B} d \Gamma }\\ &= \frac{ \displaystyle \iint_{\rm B} {W_{\rm K}}^2 d \Gamma - 2 \mu_{\rm W} \displaystyle \iint_{\rm B} W_{\rm K} d \Gamma + {\mu_{\rm W}}^2 \displaystyle \iint_{\rm B}d \Gamma }{ \displaystyle \iint_{\rm B} d \Gamma } \\ &= \frac{ \displaystyle \iint_{\rm B} {W_{\rm K}}^2 d \Gamma }{ \displaystyle \iint_{\rm B} d \Gamma } -2 \mu_{\rm W} \cdot \mu_{\rm W} +{\mu_{\rm W}}^2 = \frac{ \displaystyle \iint_{\rm B} {W_{\rm K}}^2 d \Gamma }{ \displaystyle \iint_{\rm B} d \Gamma } - {\mu_{\rm W}}^2 \tag{5.3.53} \end{align*} \] ですから、結局、式5.3.52は、 \[ {\mathcal S} \left( {\rm Q}_0 \right) = 1 - k^2 {\sigma_{\rm W}}^2 \tag{5.3.54} \] とまとめることができるわけです。 | |
 | てことは、 \[ \sigma_{\rm W} = \frac{1}{k} \sqrt{ 1- {\mathcal S} \left( {\rm Q}_0 \right) }= \frac{\lambda}{2 \pi} \sqrt{ 1- {\mathcal S} \left( {\rm Q}_0 \right) } \tag{5.3.55} \] だから、\({\mathcal S}=0.8\)のとき、\(\sigma_{\rm W} \fallingdotseq \cfrac{\lambda}{14}\)になりますね。 | |
 | 予想どおりの結果が得られました。 | |
 | こうやって見ると、Rayleigh's criterionも、Maréchal's criterionも、Strehl ratioも、同じことを別の方法で定義しているだけなんですね。 | |
 | まぁ、波面収差の良し悪しを評価する基準が、何の関連もなく複数あるよりは、合理的だと思います。後は、それぞれを使い分けたり、組み合わせて総合的に評価するなりすればよい、ということになるのです。 | |
 | う〜ん。で、結局のところ、波面収差の評価に関して言うと、何でレーザの章で取り扱うのか、よく分からないままですね。 | |
 | たぶん、Strehl ratioが中心強度の比で定義されてますし、Maréchal's criterionは、そこから派生して議論されるから、でしょう。尤も、入射する光はレーザで限定されているわけではありませんが。 | |
 | でも、実用的にレンズを測定するとなったら、一般的には波長が単一のレーザを使う、ってことか…。 | |
 | また、\(M^2\)と関連させると、無収差レンズを使った場合、Strehl ratioを満たしていれば、そのレーザはGaussianビームと見なせる、というように考えることもできます。波面収差の乱れは、レンズだけでなく、入射する光の位相情報にも依存するはずですからね。 | |
 | そうか。だから、Strehl ratioは\(M^2\)と併せて議論されることが多いんですね。 | |
 | というわけで、この講義も、いよいよラスト・スパートです。 |
| 前頁へ | 戻る | 次頁へ |