 | 最後に、レンズ設計する際に、レーザのどの仕様に着目するかについて見ていきましょう。 | |
 | 電気的な特性と、光学的な特性がありそうですね。 | |
 |
レンズ設計に必要なのは光学的な特性なので、ここでは、それに特化します。図5.4.1は、LSUで比較的よく使われるLDの仕様表を抜粋したものです。
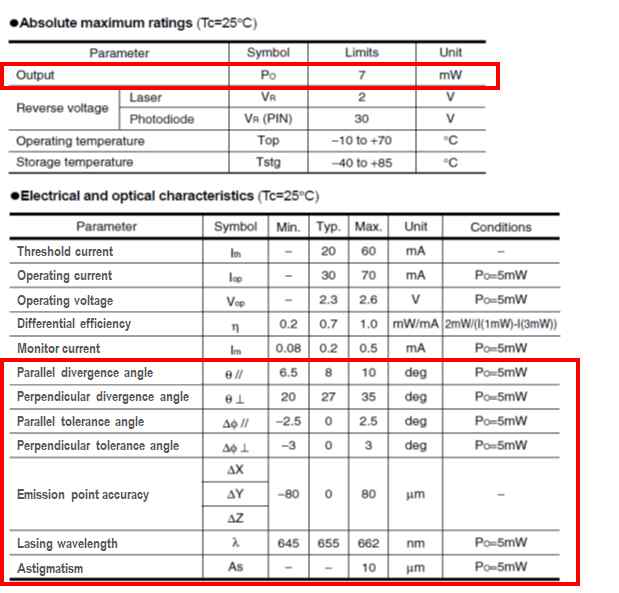 図5.4.1 レーザの仕様書(一部) |
|
 | 赤枠で囲っているのが、光学的な特性ですね。 | |
 | 1つ1つ見ていきましょう。まずは、波長(wavelength)ですね。レーザ・ポインターのようなケースはともかく、たいていの場合、放射されたレーザは、何らかの形で受光して使用するケースが多いです。そういう場合、受光する素子の感度が波長特性を持つため、相性のよい波長のLDを選定する必要があります。 | |
 | ±10nmくらい、バラつくんですね。 | |
 | そうですね。このバラツキは、温度が25℃のとき、という点に注意しなければなりません。 | |
 | ここで言っている温度って、雰囲気温度ですか?? | |
 | 違います。仕様書にあるTcはパッケージで測定した温度という意味です。 | |
 | それは、雰囲気温度とは違う?? | |
 | LDは発熱体ですからね。発光したときの自己発熱分も合わせたものになります。 | |
 | 波長そのものも、温度特性がありますよね。 | |
 | そうですね。ですから、レンズ設計をする場合、雰囲気温度がどこからどこまで変動するのかを加味し、それに伴って変動する波長も議論の対象になるのです。 | |
 | 波長が変わると、透過率も反射率も吸収も変わってきますもんね。 | |
 | 特に、受光素子の感度やDOE、バンド・パス・フィルターのように波長に対して非常に敏感な振る舞いをする素子は要注意です。 | |
 | Emission point accuracyっていうのは、発光点位置精度?? | |
 | そうです。仕様書のどこかに、メカ図面があるので、そこで指定されている基準面からのズレを示しています。尤も、これはLDを動かすなり、レンズを動かすなりして、組み付ける際に調整するのが一般的なので、その調整ストロークを見積もるのに使う数値になりますね。 | |
 | そうすると、torelance angleというのも、メカ的な角度ズレを意味している?? | |
 | はい。本当なら真っ直ぐに進むべきレーザ・ビームが上下方向、左右方向にズレて放射されるかもしれません。そのズレ量です。 | |
 | parallelとperpendicularってありますけど?? | |
 | 水平か垂直か、というのは活性層に対して定義されます。活性層と同じ方向が水平になります。 | |
 | 角度については、もう1つdivergenceというのがありますけど?? | |
 |
これは、発散角ですね。
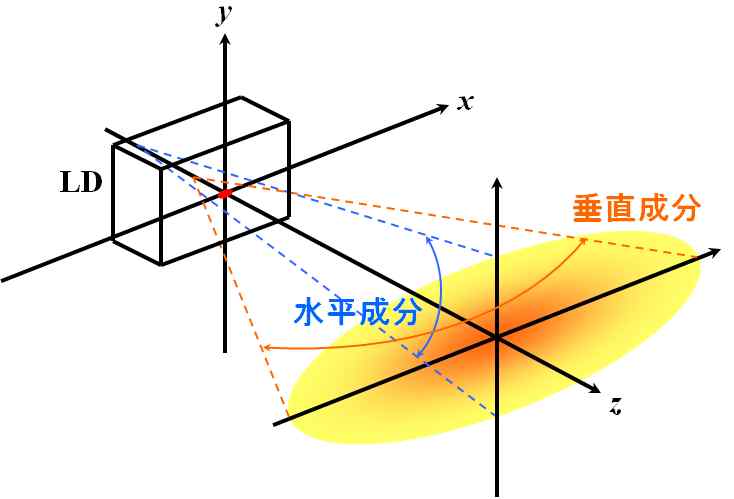 図5.4.2 発散角 発散角は、ビームの放射具合を表す指標です。 |
|
 | 回折の影響ですか?? | |
 | そうです。特に、活性層が挟まれている方向はサブμmしかないので、垂直方向の広がりの方がずっと大きくなります。だいたい、垂直方向が\(30^{\circ}\)くらい、水平方向が\(9^{\circ}\)くらいとなります。さて、ここで次のようなことを考えてみましょう。LSUのアパーチャー径を\(2D_x \times 2D_y\)、シリンダー・レンズの焦点距離を\(f_{\rm CYL}\)とすると、ポリゴン・ミラー上のビーム・スポット・サイズは、次のようになります。 \[ {\omega_x}^{\left( {\rm POL} \right)} = D_x \\ {\omega_y}^{\left( {\rm POL} \right)} = 0.61 \lambda \frac{f_{\rm CYL}}{D_y} \] | |
 | \({\omega_y}^{\left({\rm POL}\right)}\)は、式4.2.36を使ってますね。 | |
 | 更に、走査レンズの主走査方向の焦点距離を\(f_m\)、走査レンズの副走査方向の結像倍率を\(\beta_s\)とすると、感光体上のビーム・スポット・サイズは、 \[ {\omega_x} = 0.61 \lambda \frac{f_m}{{\omega_x}^{\left( {\rm POL} \right)}} = 0.61 \lambda \frac{f_m}{D_x} \\ {\omega_y} = {\omega_y}^{\left( {\rm POL} \right)} \times \beta_s = 0.61 \lambda \frac{f_{\rm CYL}}{D_y} \times \beta_s \] です。 | |
 | \(\omega_y\)は、式5.2.73を使ってますね。 | |
 | 議論の見通しをよくするために、\(\omega_x = \omega_y\)とすると、 \[ \frac{f_m}{D_x} = \frac{f_{\rm CYL}}{D_y} \times \beta_s \quad \Leftrightarrow \quad \frac{D_y}{D_x} = \frac{f_{\rm CYL} \times \beta_s}{f_m} \tag{5.4.1} \] です。A3サイズのLSUでは\(f_m\)=210mm、また経験的に\(f_{\rm CYL}\)=70mm、\(\beta_s\)=0.7~2.0なので、式5.4.1は\(\cfrac{D_y}{D_x} \approx \cfrac{1}{3}\)。つまり、感光体上で丸いビーム・スポットを形成したいのであれば、アパーチャーは\(D_x > D_y\)となるわけです。 | |
 | でも、一般的には、感光体上のビーム・スポットって、走査方向にエネルギーが加算されているから、それを考慮して\(y\)方向に細長い楕円形状をしてませんか?? | |
 | はい。しかし、楕円率が3にもなるような細長い楕円にはなりません。ですから、アパーチャーが\(x\)方向に長い形状になることは普通であると言えます。そうすると、LDの設定は、発散角の大きい方を\(x\)方向に合わせたくなりませんか?? | |
 | その方が、たくさん光量を取り込めるからですね?? | |
 | つまり、活性層の向きは\(y\)方向ということです。そして、LDの直線偏光は活性層と平行でしたから―。 | |
 | なるほど。それで、LDは、ポリゴン・ミラーに対して\(s\)偏光となるように設置するわけですね。 | |
 | ずいぶん前の疑問でしたが、ようやく回答にたどりつきました。 | |
 | 教授。発散角を定義するには、ピーク強度の何\(\%\)みたいな取り決めが必要だと思うんですけど?? | |
 | そうですね。普通は、ピーク強度の\(50\%\)の輪帯です。 | |
 | う~ん。Gaussianビームを議論したときは、ビーム・スポット・サイズをピーク強度の\(\cfrac{1}{\mathrm{e}^2}\)となる拡がりで定義してましたよね??そうすると、換算が必要では?? | |
 |
そうなりますね。でも、それほど難しい話ではないですよ。レーザから放射されたビームの、LDから充分に離れた強度分布をFFP(ファー・フィールド・パタン)と言います。Gaussianビームの場合、このFFPがGauss分布になっているのです。
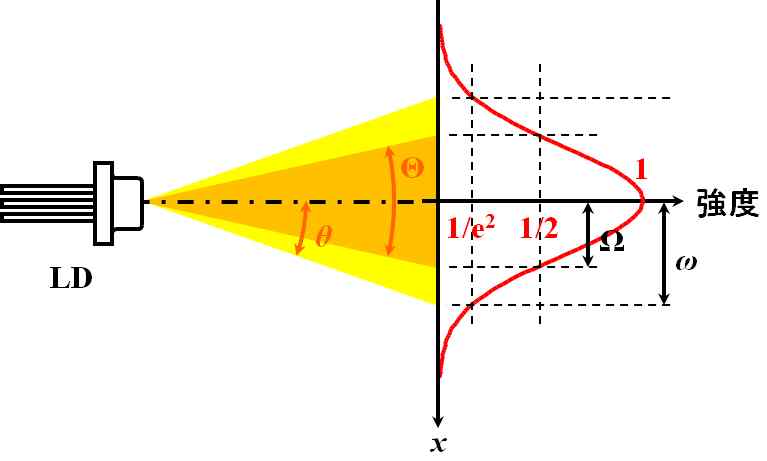 図5.4.3 発散角の変換 図5.4.3で、レーザの半値全角を\(\Theta\)、このときのビームの径を\(\Omega\)とすると、ビーム拡がり角\(\theta\)、ビーム・スポット・サイズ\(\omega\)との関係は、 \[ \cfrac{\Omega}{\tan \left( \cfrac{\Theta}{2} \right)} = \frac{\omega}{\tan \theta} \quad \Leftrightarrow \quad \Omega = \omega \frac{\tan \left( \cfrac{\Theta}{2} \right)}{\tan \theta} \tag{5.4.2} \] のようになります。式5.4.2を式5.2.18に代入すると?? |
|
 | こうかな。 \[ \cfrac{1}{2} = \exp \left[ - \cfrac{2}{\omega^2} \left( \omega \cfrac{\tan \left( \Theta/2 \right)}{\tan \theta} \right)^2 \right] = \exp \left[ - 2 \left( \cfrac{\tan \left( \Theta/2 \right)}{\tan \theta} \right)^2 \right]\tag{5.4.3} \] | |
 | 両辺の自然対数をとって、整理してみてください。 | |
 | ん~と。 \[ \begin{align*} - \ln 2 &= - 2 \left( \cfrac{\tan \left( \Theta/2 \right)}{\tan \theta} \right)^2 \quad \Leftrightarrow \quad \frac{\ln 2}{2} = \left( \cfrac{\tan \left( \Theta/2 \right)}{\tan \theta} \right)^2 \\ &\quad \Leftrightarrow \quad \sqrt{\frac{\ln 2}{2}} = \cfrac{\tan \left( \cfrac{\Theta}{2} \right)}{\tan \theta} \quad \Leftrightarrow \quad \tan \theta = \sqrt{\frac{2}{\ln 2}} \tan \left( \cfrac{\Theta}{2} \right) \\ &\quad \Leftrightarrow \quad \theta = \tan^{-1} \left[ \sqrt{\frac{2}{\ln 2}} \tan \left( \cfrac{\Theta}{2} \right) \right] \tag{5.4.4} \end{align*} \] かな。 | |
 | これが、求めるべき換算公式です。 | |
 | Astigmatismというのは?? | |
 |
これは非点隔差と呼ばれるものですね。LDから放射されたビームは、以前やったように双曲線関数に従って拡がっていきます。このとき、\(x\)方向と\(y\)方向で漸近線を定義できますが、一般に、この漸近線の交点は\(x\)方向と\(y\)方向で一致しません。このときの\(z\)方向のズレ量が非点隔差です。
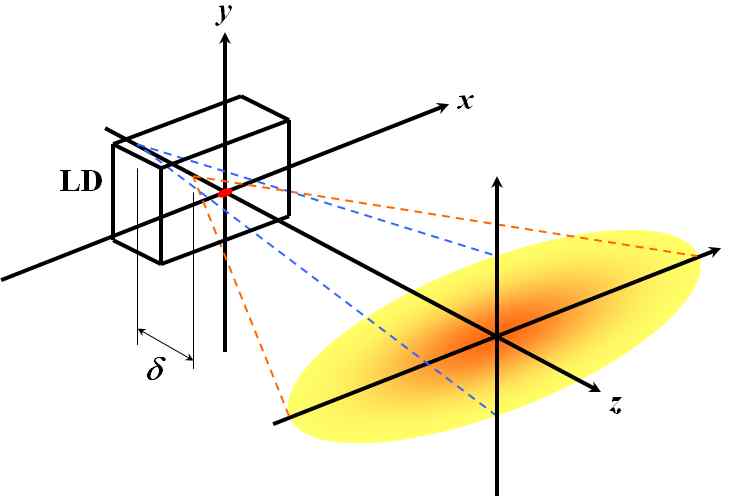 図5.4.4 非点隔差 |
|
 | でも、高々10μmしかないから、あまり気にならないのでは?? | |
 | そうですね。LDを使ってどんな装置を作るかにもよりますが、LSUの設計で、ここが争点になることはありません。また、仮に非点隔差が問題になる場合には、アナモルフィックなレンズを使えば簡単に解決できます。 | |
 | Outputは出力だから、LSUの場合、光学系の透過率・反射率を考慮して、感光体の露光エネルギーよりも大きな光エネルギーになるようなパワーであれば、問題ないってことですね。 | |
 | あとは、目に対する安全規格についても充分な配慮が求められますね。 | |
 | そうか。 | |
 | また、感光体に到達する光エネルギーは、アパーチャーを通過するときのカップリング効率(=アパーチャーを通過する光量の割合)が非常に問題になります。 | |
 | どうしてですか?? | |
 | カップリング効率は、発散角の変化によって、かなりダイナミックに変動するからですよ。 | |
 | そんなに変動しますか?? | |
 | 変動しますね。それは、ちょっと計算して確認すれば、すぐに理解できます。簡単のために、発散角は平行成分も垂直成分も\(40^{\circ}\)と仮定しましょう。 | |
 | F.F.Pは円形ってことですね。 | |
 |
そして、コリメーター・レンズで平行光束に変換した後、アパーチャーを照射します。このアパーチャーは、ビーム強度の\(\cfrac{1}{2}\)以上となる領域を内接する正方形とします。
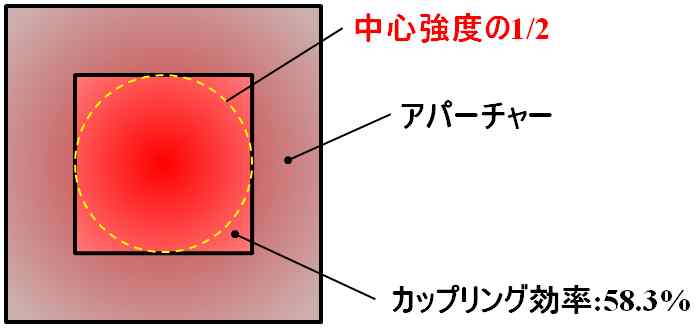 図5.4.5 カップリング効率 このとき、カップリング効率は\(58.3\%\)です。 |
|
 | どうやって計算しているんですか?? | |
 | excelで強度分布の計算を行い、アパーチャーへの取り込み割合を求めています。 | |
 | この辺は、泥臭くやるしかないのか。 | |
 | 一方、発散角が\(20^{\circ}\)になると、カップリング効率は\(86.1\%\)です。 | |
 | お、かなり変動しますね。 | |
 | 逆に、\(40^{\circ}\)だと、\(38.0\%\)ですから、変動がダイナミックだというのは、誇張でも何でもないわけです。 | |
 | そうすると、もしカップリング効率を変動させたくなければ、アパーチャーなんかない方がいい、ってことになりますね。 | |
 |
図5.4.6は、アパーチャーを「ビーム強度の○○\(\%\)以上となる領域を内接する正方形」と定義したとき、この○○を横軸、縦軸をカップリング効率にとり、発散角が\(30^{\circ}\)と\(20^{\circ}\)のときの変化を示したものです。
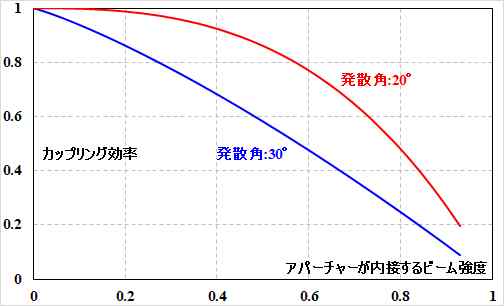 図5.4.6 発散角の変動とカップリング効率の関係 これを見ると、確かにアパーチャーがなければ(=横軸が\(0\)近傍)、発散角が変わったところでカップリング効率は\(100\%\)のままです。が、感光体上のビーム・スポットの安定性という観点から言えば、発散角が変わるということは瞳関数が変わるということでもあるので、好ましくありません。 |
|
 | ビーム・スポットの安定性とカップリング効率の安定性を満たすには、アパーチャーはビームに対して小さく設定する(=横軸が\(1\)近傍)しかないけど…。でも、それだとカップリング効率は小さくなるから、感光体を露光できなくなっちゃいますね。 | |
 | そうです。これらをバランスさせるのが、LSUの設計の肝になるわけです。 | |
 | アパーチャー上の瞳関数は、LDの発散角とコリメーター・レンズの焦点距離が決まれば一義的に求まりそうですね。 | |
 | 焦点距離を長くすれば、強度分布の強い領域だけを利用することができます。 | |
 | スイカも、中心部分が一番甘くて美味しいです。 | |
 | …。しかし、その反面、カップリング効率は小さくなっていきます。ここで、1つのバランスを考慮しないといけません。 | |
 | アパーチャーは感光体上のビーム・スポット・サイズを決める重要なファクターだから、ここでもバランスを考慮しないといけませんね。 | |
 | 更に、発散角の変動です。これによってカップリング効率が変動しますから、それでも充分に感光体を露光するだけのエネルギーを届けられないといけない。そこで、LDの出力とのバランスの問題が出てきます。 | |
 | そういう中で、走査レンズの設計を他の光学特性を考慮しながら詰めていくわけか…。これは大変だ。 | |
 | もし、どうしてもバランスがとれない場合、例えばLDの発散角の仕様を狭くするなどの手を打つこともありますね。 | |
 | 選別するみたいなこと?? | |
 | そうです。こちらが必要とする仕様をメーカーに投げて、仕分けてもらうのです。 | |
 | コストが掛かりそうですね…。 | |
 | だから、最終手段です。他には、アパーチャーの形状を工夫したりもします。 | |
 | 例えば?? | |
 |
では、最後にアパーチャーのコレクションをお見せしましょう。
 図5.4.7 矩形アパーチャー |
|
 | これは矩形に見えますね。 | |
 |
非常にオーソドックスなアパーチャーと言えるでしょう。一般的には、アルミを打ち抜いて加工します。次は、これですね。
 図5.4.8 楕円アパーチャー |
|
 | 楕円ですね。そうか。F.F.P.が楕円形状だから、それに合わせているわけですね?? | |
 |
そうです。こうすることで、4隅の光強度の弱い部分をカットし、発散角の変動によるカップリング効率の変動を抑えているわけです。同じ効果を狙ったものとして、変わった形のアパーチャーが図5.4.9になります。
 図5.4.9 H形アパーチャー |
|
 | お~、H形だ。 | |
 | 旧富士ゼロックス㈱のLSUに搭載されていたものです。こういうように、アパーチャー1つとっても、開発者はいろいろなアイデアを出して、課題の解決を図っているんですよ。 |
| 前頁へ | 戻る |